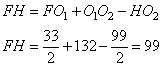Задание 25 из 50 вариантов ОГЭ для тренировки
Окружности радиусов 33 и 99 касаются внешним образом. Точки A и B лежат на первой окружности, точки С и D — на второй. При этом АС и BD — общие касательные окружностей. Найдите расстояние между прямыми АВ и CD.
Решение.
Так как AC и BD – касательные, то 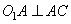 ,
, 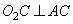 . Также
. Также 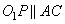 (так как ACPO1 – прямоугольник), следовательно, PO2=99-33=66, так как AO1=33, CO2=99. А расстояние между центрами окружностей O1O2=33+99=132.
(так как ACPO1 – прямоугольник), следовательно, PO2=99-33=66, так как AO1=33, CO2=99. А расстояние между центрами окружностей O1O2=33+99=132.
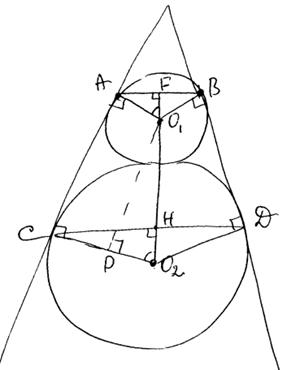
Рассмотрим прямоугольный треугольник O1PO2, из которого имеем:
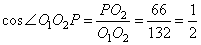
то есть, 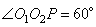 и
и 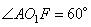 , так как они соответственные. Рассмотрим прямоугольный треугольник AFO1, в котором
, так как они соответственные. Рассмотрим прямоугольный треугольник AFO1, в котором 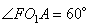 , следовательно,
, следовательно, 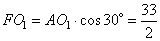 . Из прямоугольного треугольника CHO2 по аналогии, получаем:
. Из прямоугольного треугольника CHO2 по аналогии, получаем: 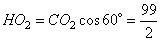 . Таким образом, расстояние между прямыми AB и CD, равно:
. Таким образом, расстояние между прямыми AB и CD, равно:
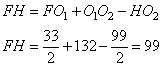
Ответ: 99.
Задание 25 . Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки С и D — на второй. При этом АС и BD — общие касательные окружностей. Найдите расстояние между прямыми АВ и CD.
Ответ: 112
. Задание 25 . Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки С и D — на второй. При этом АС и BD — общие касательные окружностей. Найдите расстояние между прямыми АВ и CD.
Ответ: 120
Задание 25 . Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружности, точки С и D — на второй. При этом АС и BD — общие касательные окружностей. Найдите расстояние между прямыми АВ и CD.
Ответ: 80
Задание 25 . Окружности радиусов 36 и 45 касаются внешним образом. Точки A и B лежат на первой окружности, точки С и D — на второй. При этом АС и BD — общие касательные окружностей. Найдите расстояние между прямыми АВ и CD.
Ответ: 80
Задание 25 . Окружности радиусов 42 и 84 касаются внешним образом. Точки A и B лежат на первой окружности, точки С и D — на второй. При этом АС и BD — общие касательные окружностей. Найдите расстояние между прямыми АВ и CD.
Ответ: 112