ЗАДАНИЕ 25 ОГЭ.
ЧЕТЫРЁХУГОЛЬНИКИ И ИХ ЭЛЕМЕНТЫ.
(77, 315010) В параллелограмме  проведены перпендикуляры
проведены перпендикуляры 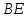 и
и 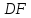 к диагонали
к диагонали 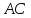 (см. рисунок). Докажите, что
(см. рисунок). Докажите, что 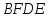 — параллелограмм.
— параллелограмм. 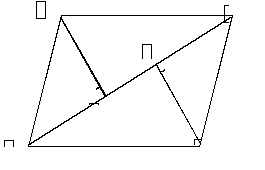
Решение.
Для того, чтобы доказать, что четырёхугольник является параллелограммом, достаточно доказать, что у него противоположные стороны равны и параллельны (признак параллелограмма).
Рассмотрим 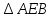 и
и  .
.

(по признаку равенства прямоугольных треугольников: «если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны»). Значит, все соответствующие стороны и углы этих треугольников равны, а именно: 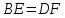 .
.
Кроме того,
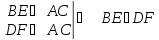 (по признаку параллельности прямых: «если две прямые перпендикулярны третьей прямой, то они параллельны»).
(по признаку параллельности прямых: «если две прямые перпендикулярны третьей прямой, то они параллельны»).
Итак, 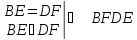 – параллелограмм ( по признаку параллелограмма), ч.т.д.
– параллелограмм ( по признаку параллелограмма), ч.т.д.
(340935) Сторона  параллелограмма
параллелограмма  вдвое больше стороны
вдвое больше стороны  . Точка
. Точка 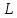 — середина стороны
— середина стороны 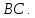 Докажите, что
Докажите, что 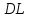 — биссектриса угла
— биссектриса угла 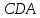 .
.
Решение.
По условию задачи 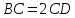 . Т.к.
. Т.к. 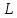 - середина
- середина  , то
, то 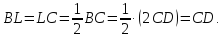 Значит,
Значит, 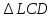 – равнобедренный с основанием
– равнобедренный с основанием  . Тогда, по свойству равнобедренного треугольника, углы при основании равны, т.е.
. Тогда, по свойству равнобедренного треугольника, углы при основании равны, т.е.  .
.  как внутренние накрест лежащие при параллельных прямых. Итак,
как внутренние накрест лежащие при параллельных прямых. Итак,
 (как углы, равные одному и тому же углу). Значит, по определению биссектрисы угла,
(как углы, равные одному и тому же углу). Значит, по определению биссектрисы угла, 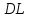 – биссектриса
– биссектриса  , ч.т.д.
, ч.т.д.
(341344) Биссектрисы углов  и
и  трапеции
трапеции  пересекаются в точке
пересекаются в точке  , лежащей на стороне
, лежащей на стороне  . Докажите, что точка
. Докажите, что точка  равноудалена от прямых
равноудалена от прямых  ,
,  и
и  .
.
Решение.
I способ. По свойству биссектрисы угла, так как точка  лежит на биссектрисе
лежит на биссектрисе  , то она равноудалена от прямых
, то она равноудалена от прямых  и
и  . Так как эта же точка
. Так как эта же точка  лежит на биссектрисе
лежит на биссектрисе  , то она равноудалена от прямых BC и CD. Значит, точка
, то она равноудалена от прямых BC и CD. Значит, точка  равноудалена от прямых
равноудалена от прямых  ,
,  и
и  , ч.т.д.
, ч.т.д.
II способ. Расстояние от точки до прямой определяется по перпендикуляру, поэтому проведём из точки  перпендикуляры к сторонам
перпендикуляры к сторонам  ,
,  и
и  и докажем, что эти перпендикуляры равны.
и докажем, что эти перпендикуляры равны.
Рассмотрим  и
и  .
.
(по признаку равенства прямоугольных треугольников: «если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны»). Значит,  .
.
Рассмотрим  и
и  .
.
(по признаку равенства прямоугольных треугольников). Значит,  .
.
Итак, , ч.т.д.
(341396, 349074) Точка  — середина боковой стороны
— середина боковой стороны  трапеции
трапеции  . Докажите, что площадь треугольника
. Докажите, что площадь треугольника  равна половине площади трапеции.
равна половине площади трапеции.
Решение.
I способ. Проведём дополнительное построение.  .
.
Рассмотрим  и
и  .
.
 (по II признаку равенства треугольников)
(по II признаку равенства треугольников)
Рассмотрим  .
.  – медиана
– медиана  (по свойству медианы треугольника)
(по свойству медианы треугольника) , ч.т.д.
, ч.т.д.
II способ. Проведём высоты трапеции  и
и  .
.
.
Рассмотрим  и
и  .
.
(по признаку равенства прямоугольных треугольников).
;
, ч.т.д.
(341511, 340347) Докажите, что отрезок, соединяющий середины оснований трапеции, делит её на две равные по площади части.
Решение.
Пусть точка  – середина основания
– середина основания  трапеции
трапеции  , а точка
, а точка  – середина основания
– середина основания  . Тогда отрезок
. Тогда отрезок  делит трапецию
делит трапецию  на две трапеции:
на две трапеции:  и
и  . Проведём высоты
. Проведём высоты  и
и  трапеции
трапеции  и найдём площади получившихся трапеций
и найдём площади получившихся трапеций  и
и  .
.
Так как и  , то
, то  , ч.т.д.
, ч.т.д.
(155, 314849) В параллелограмме  точки
точки  ,
,  ,
,  и
и  лежат на его сторонах, как на рисунке, причём . Докажите, что
лежат на его сторонах, как на рисунке, причём . Докажите, что  — параллелограмм.
— параллелограмм.
Решение.
Для того, чтобы доказать, что четырёхугольник является параллелограммом, достаточно доказать, что у него противоположные стороны попарно равны (признак параллелограмма).
Докажем сначала равенство отрезков 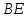 и
и  . Используем III аксиому планиметрии («Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разделён какой-нибудь точкой»)
. Используем III аксиому планиметрии («Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разделён какой-нибудь точкой»)


 по свойству сторон параллелограмма;
по свойству сторон параллелограмма;  по условию. Значит,
по условию. Значит,  .
.
Аналогично доказывается, что  .
.
Рассмотрим  и
и  .
.
по I признаку равенства треугольников 
Рассмотрим  и
и  .
.
по I признаку равенства треугольников 
Итак, у четырёхугольника  стороны попарно равны, значит, этот четырёхугольник является параллелограммом, ч.т.д.
стороны попарно равны, значит, этот четырёхугольник является параллелограммом, ч.т.д.
(181, 315120) Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
Решение.
Так как восьмиугольник правильный, то у него все стороны и все углы равны, причём его угол вычисляется по формуле: 
.
По I признаку равенства треугольников («Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны»):
.
Кроме того, эти же равные треугольники являются равнобедренными, значит, углы при основаниях у них равны, т.е.
Тогда . Значит, все углы четырёхугольника  – прямые.
– прямые.
Итак, у четырёхугольника  все углы прямые и все стороны равны, значит, такой четырёхугольник является квадратом, ч.т.д.
все углы прямые и все стороны равны, значит, такой четырёхугольник является квадратом, ч.т.д.
(315039) Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
Решение.
Так как исходный шестиугольник правильный, то у него все стороны и все углы равны. Каждую сторону разделили пополам точками и соединили эти точки. Получили равные равнобедренные треугольники (I признак равенства треугольников). Значит, стороны у получившегося шестиугольника равны. Каждый угол этого шестиугольника является разностью  (развёрнутого угла) и суммы двух равных углов (углы при основании равнобедренного треугольника). Значит, в полученном шестиугольнике все стороны и углы равны, значит, он является правильным, ч.т.д.
(развёрнутого угла) и суммы двух равных углов (углы при основании равнобедренного треугольника). Значит, в полученном шестиугольнике все стороны и углы равны, значит, он является правильным, ч.т.д.
(51, 3112603, 311555, 311696, 314812, 314895, 314919) В параллелограмме  точка
точка  — середина стороны
— середина стороны  . Известно, что
. Известно, что  . Докажите, что данный параллелограмм — прямоугольник.
. Докажите, что данный параллелограмм — прямоугольник.
Решение.
Рассмотрим  и
и  .
.
 (по III признаку равенства треугольников)
(по III признаку равенства треугольников) . Эти углы являются внутренними односторонними при параллельных прямых, значит, .
. Эти углы являются внутренними односторонними при параллельных прямых, значит, .
По свойству углов параллелограмма,  . Значит, в параллелограмме
. Значит, в параллелограмме  все углы прямые, поэтому, данный параллелограмм является прямоугольником, ч.т.д.
все углы прямые, поэтому, данный параллелограмм является прямоугольником, ч.т.д.
(311663, 311573) В параллелограмме  проведены высоты
проведены высоты 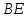 и
и  . Докажите, что
. Докажите, что  подобен
подобен  .
.
Решение.
Рассмотрим  и
и  .
.
(по I признаку подобия треугольников), ч.т.д.
(311603) В параллелограмме проведены биссектрисы противоположных углов. Докажите, что отрезки биссектрис, заключённые внутри параллелограмма, равны.
Решение.
Пусть  и
и  – биссектрисы
– биссектрисы  и
и  соответственно. Тогда, . Так как, по свойству углов параллелограмма,
соответственно. Тогда, . Так как, по свойству углов параллелограмма,  , то
, то  .
.
Рассмотрим  и
и  .
.
(по II признаку равенства треугольников). Следовательно, все соответствующие стороны и углы этих треугольников равны, а конкретно,  , ч.т.д.
, ч.т.д.
(311608) Середины сторон параллелограмма являются вершинами ромба. Докажите, что данный параллелограмм — прямоугольник.
Решение.
Рассмотрим  и
и  .
.
 (по III признаку равенства треугольников)
(по III признаку равенства треугольников) . Эти углы являются внутренними односторонними при параллельных прямых, значит, .
. Эти углы являются внутренними односторонними при параллельных прямых, значит, .
По свойству углов параллелограмма,  . Значит, в параллелограмме
. Значит, в параллелограмме  все углы прямые, поэтому, данный параллелограмм является прямоугольником, ч.т.д.
все углы прямые, поэтому, данный параллелограмм является прямоугольником, ч.т.д.
(311607) Дана равнобедренная трапеция  . Точка
. Точка  лежит на основании
лежит на основании  и равноудалена от концов другого основания. Докажите, что
и равноудалена от концов другого основания. Докажите, что  — середина основания
— середина основания  .
.
Решение.
Так как  то
то  – равнобедренный, следовательно,
– равнобедренный, следовательно,  . Так как трапеция
. Так как трапеция  – равнобедренная, то
– равнобедренная, то  .
.
Рассмотрим  и
и  .
.
(по I признаку равенства треугольников), следовательно,  , значит,
, значит,  – середина основания
– середина основания  , ч.т.д.
, ч.т.д.
(311667) Три стороны параллелограмма равны. Докажите, что отрезок с концами в серединах противоположных сторон параллелограмма равен четверти его периметра.
Решение.
Пусть точка  – середина стороны
– середина стороны  , а точка
, а точка  – середина стороны
– середина стороны  . В параллелограмме противоположные стороны равны. Так как, по условию, три стороны равны, значит, равны все четыре стороны. По определению параллелограмма, . Кроме того,
. В параллелограмме противоположные стороны равны. Так как, по условию, три стороны равны, значит, равны все четыре стороны. По определению параллелограмма, . Кроме того,
. Значит, в четырёхугольнике две стороны параллельны и равны, поэтому, этот четырёхугольник является параллелограммом (по признаку параллелограмма). Следовательно,  .
.
, ч.т.д.
(311925) В параллелограмме  проведены высоты
проведены высоты  и
и 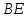 к сторонам
к сторонам  и
и  соответственно, при этом
соответственно, при этом  . Докажите, что
. Докажите, что  — ромб.
— ромб.
Решение.
Рассмотрим  и
и  .
.
(по признаку равенства прямоугольных треугольников: «Если катет и острый угол одного прямоугольного треугольника равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны»). Следовательно, все соответствующие углы и стороны этих треугольников равны, а именно,  . Учитывая, что у параллелограмма противоположные стороны равны, получаем:
. Учитывая, что у параллелограмма противоположные стороны равны, получаем:  , а это означает, что
, а это означает, что  – ромб, ч.т.д.
– ромб, ч.т.д.
(314822, 314977, 314987) В параллелограмме  диагонали
диагонали 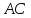 и
и  пересекаются в точке
пересекаются в точке  . Докажите, что площадь параллелограмма
. Докажите, что площадь параллелограмма  в четыре раза больше площади треугольника
в четыре раза больше площади треугольника  .
.
Решение.
Проведём высоту параллелограмма  .
.
Рассмотрим  и
и  .
.
(по II признаку равенства треугольников) .
.
Для доказательства равенства этих треугольников можно использовать признак равенства прямоугольных треугольников по гипотенузе и острому углу.
Значит,  .
.
, ч.т.д.
(315047) Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
Решение.
Так как шестиугольник правильный, то у него все стороны и все углы равны. Значит, по I признаку равенства треугольников (по двум сторонам и углу между ними). Следовательно,  , а это значит, что треугольник
, а это значит, что треугольник  – равносторонний, ч.т.д.
– равносторонний, ч.т.д.
(333131, 349523, 333322) Внутри параллелограмма  выбрали произвольную точку
выбрали произвольную точку  . Докажите, что сумма площадей треугольников
. Докажите, что сумма площадей треугольников  и
и  равна половине площади параллелограмма.
равна половине площади параллелограмма.
Решение.
Проведём высоту параллелограмма  через точку
через точку  .
.
. Здесь мы учли свойство сторон параллелограмма ( ) и использовали формулу площади параллелограмма (). Утверждение доказано.
) и использовали формулу площади параллелограмма (). Утверждение доказано.
(339506) Основания  и
и  трапеции
трапеции  равны соответственно
равны соответственно  и
и  ,
,  . Докажите, что треугольники
. Докажите, что треугольники  и
и  подобны.
подобны.
Решение.
Рассмотрим  и
и  .
.
 (по II признаку подобия треугольников (по двум пропорциональным сторонам и углу между ними)), ч.т.д.
(по II признаку подобия треугольников (по двум пропорциональным сторонам и углу между ними)), ч.т.д.
(340387, 357080) Биссектрисы углов  и
и  параллелограмма
параллелограмма  пересекаются в точке
пересекаются в точке  стороны
стороны  . Докажите, что
. Докажите, что  — середина
— середина  .
.
Решение.
I способ. Пусть  , тогда по свойству внутренних односторонних углов при параллельных прямых. Так как
, тогда по свойству внутренних односторонних углов при параллельных прямых. Так как  и
и 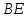 – биссектрисы этих углов, то
– биссектрисы этих углов, то
.
По свойству углов параллелограмма . Из . А это означает, что  - равнобедренный, т.е.
- равнобедренный, т.е.  .
.
Из . Это означает, что  - равнобедренный, т.е.
- равнобедренный, т.е.  .
.
Итак, , т.е. точка  – середина стороны
– середина стороны  , ч.т.д.
, ч.т.д.
II способ. Проведём через точку  прямую, параллельную сторонам
прямую, параллельную сторонам  и
и  . Получили два параллелограмма
. Получили два параллелограмма  и
и  . В каждом из этих параллелограммов диагональ является биссектрисой (
. В каждом из этих параллелограммов диагональ является биссектрисой ( и
и  ). А это является признаком ромба, т.е. и точка
). А это является признаком ромба, т.е. и точка  – середина
– середина  , ч.т.д.
, ч.т.д.
(339625) В выпуклом четырёхугольнике  углы
углы  и
и  равны. Докажите, что углы
равны. Докажите, что углы  и
и  также равны.
также равны.
Решение.
Рассмотрим  и
и  .
.
 (по I признаку подобия треугольников)
(по I признаку подобия треугольников)
(по свойству пропорции)  .
.
Рассмотрим  и
и  .
.
(по II признаку подобия треугольников). Следовательно, все соответствующие углы у этих треугольников равны, а именно,  , а значит,
, а значит,  , ч.т.д.
, ч.т.д.
(340055) В трапеции  с основаниями
с основаниями  и
и  диагонали пересекаются в точке
диагонали пересекаются в точке  . Докажите, что площади треугольников
. Докажите, что площади треугольников  и
и  равны.
равны.
Решение.
I способ. Рассмотрим  и
и  .
.
(по I признаку подобия треугольников)
по свойству вертикальных углов.
, ч.т.д.
II способ.
Рассмотрим  и
и  , и покажем, что их площади равны. Проведём две высоты трапеции
, и покажем, что их площади равны. Проведём две высоты трапеции  и
и  . Очевидно, что
. Очевидно, что  . Найдём площади треугольников
. Найдём площади треугольников  и
и 
.
Теперь выразим площади  и
и  :
:
, ч.т.д.
(340104) Через точку  пересечения диагоналей параллелограмма
пересечения диагоналей параллелограмма  проведена прямая, пересекающая стороны
проведена прямая, пересекающая стороны  и
и  в точках
в точках  и
и  соответственно. Докажите, что
соответственно. Докажите, что  .
.
Решение.
Рассмотрим  и
и  .
.
 (по II признаку равенства треугольников). Следовательно, все соответствующие стороны и углы этих треугольников равны, а именно,
(по II признаку равенства треугольников). Следовательно, все соответствующие стороны и углы этих треугольников равны, а именно,  , ч.т.д.
, ч.т.д.
(340370) Известно, что около четырёхугольника  можно описать окружность и что продолжения сторон
можно описать окружность и что продолжения сторон  и
и  четырёхугольника пересекаются в точке
четырёхугольника пересекаются в точке  . Докажите, что треугольники
. Докажите, что треугольники  и
и  подобны.
подобны.
Решение.
Около четырёхугольника можно описать окружность, если сумма противоположных углов этого четырёхугольника равна  . Т.к. в условии задачи чётко сказано, что описать окружность можно, то
. Т.к. в условии задачи чётко сказано, что описать окружность можно, то
. Однако,  является смежным с
является смежным с  , значит, их сумма тоже равна
, значит, их сумма тоже равна  . Итак,
. Итак,
.
Теперь рассмотрим  и
и  .
.
(по I признаку подобия треугольников), ч.т.д.
ЗАДАЧИ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.

(207) В параллелограмме  проведены перпендикуляры
проведены перпендикуляры 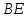 и
и 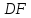 к диагонали
к диагонали 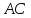 (см. рисунок). Докажите, что отрезки
(см. рисунок). Докажите, что отрезки  и
и  параллельны.
параллельны.

(315033) В параллелограмме  проведены перпендикуляры
проведены перпендикуляры 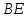 и
и 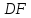 к диагонали
к диагонали 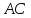 (см. рисунок). Докажите, что отрезки
(см. рисунок). Докажите, что отрезки  и
и  равны.
равны.

(315096) В параллелограмме  проведены перпендикуляры
проведены перпендикуляры 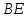 и
и 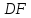 к диагонали
к диагонали 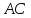 (см. рисунок). Докажите, что треугольники
(см. рисунок). Докажите, что треугольники  и
и  равны.
равны.
(357103, 339609) Биссектрисы углов  и
и  трапеции
трапеции  пересекаются в точке
пересекаются в точке  , лежащей на стороне
, лежащей на стороне  . Докажите, что точка
. Докажите, что точка  равноудалена от прямых
равноудалена от прямых  ,
,  и
и  .
.
(357105) Биссектрисы углов  и
и  трапеции
трапеции  пересекаются в точке
пересекаются в точке  , лежащей на стороне
, лежащей на стороне  . Докажите, что точка
. Докажите, что точка  равноудалена от прямых
равноудалена от прямых  ,
,  и
и  .
.
(357107) Биссектрисы углов  и
и  трапеции
трапеции  пересекаются в точке
пересекаются в точке  , лежащей на стороне
, лежащей на стороне  . Докажите, что точка
. Докажите, что точка  равноудалена от прямых
равноудалена от прямых  ,
,  и
и  .
.
(357124) Сторона  параллелограмма
параллелограмма  вдвое больше стороны
вдвое больше стороны  . Точка
. Точка  — середина стороны
— середина стороны  . Докажите, что
. Докажите, что  — биссектриса угла
— биссектриса угла  .
.
(353517) Сторона  параллелограмма
параллелограмма  вдвое больше стороны
вдвое больше стороны  . Точка
. Точка  — середина стороны
— середина стороны  . Докажите, что
. Докажите, что  — биссектриса угла
— биссектриса угла  .
.
(357125, 341370) Сторона  параллелограмма
параллелограмма  вдвое больше стороны
вдвое больше стороны  . Точка
. Точка 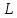 — середина стороны
— середина стороны  . Докажите, что
. Докажите, что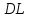 — биссектриса угла
— биссектриса угла  .
.
(357126, 341537) Сторона  параллелограмма
параллелограмма  вдвое больше стороны
вдвое больше стороны  . Точка
. Точка  — середина стороны
— середина стороны  . Докажите, что
. Докажите, что  — биссектриса угла
— биссектриса угла 
(357127) Сторона  параллелограмма
параллелограмма  вдвое больше стороны
вдвое больше стороны  . Точка
. Точка  — середина стороны
— середина стороны  . Докажите, что
. Докажите, что  — биссектриса угла
— биссектриса угла 
(357128) Сторона  параллелограмма
параллелограмма  вдвое больше стороны
вдвое больше стороны  . Точка
. Точка  — середина стороны
— середина стороны  . Докажите, что
. Докажите, что  — биссектриса угла
— биссектриса угла  .
.
(357129) Сторона  параллелограмма
параллелограмма  вдвое больше стороны
вдвое больше стороны  . Точка
. Точка  — середина стороны
— середина стороны  . Докажите, что
. Докажите, что  — биссектриса угла
— биссектриса угла  .
.
(340969) Сторона  параллелограмма
параллелограмма  вдвое больше стороны
вдвое больше стороны  . Точка
. Точка  — середина стороны
— середина стороны  . Докажите, что
. Докажите, что  — биссектриса угла
— биссектриса угла  .
.
(315075) В параллелограмме  точки
точки  ,
,  и
и  лежат на его сторонах, как показано на рисунке, причём . Докажите, что
лежат на его сторонах, как показано на рисунке, причём . Докажите, что  — параллелограмм.
— параллелограмм.
(315087) В параллелограмме  точки
точки  и
и  лежат на его сторонах, как показано на рисунке, причём
лежат на его сторонах, как показано на рисунке, причём  Докажите, что
Докажите, что  — параллелограмм.
— параллелограмм.
(315110) В параллелограмме  точки
точки  и
и  лежат на его сторонах, как показано на рисунке, причём
лежат на его сторонах, как показано на рисунке, причём  . Докажите, что
. Докажите, что  — параллелограмм.
— параллелограмм.
(311251, 314810, 314886, 314900, 314915, 314922, 314911) В параллелограмме  точка
точка  — середина стороны
— середина стороны  . Известно, что
. Известно, что  . Докажите, что данный параллелограмм — прямоугольник.
. Докажите, что данный параллелограмм — прямоугольник.
(311259, 314881, 314908) В параллелограмме  точка
точка  — середина стороны
— середина стороны  . Известно, что
. Известно, что  . Докажите, что данный параллелограмм — прямоугольник.
. Докажите, что данный параллелограмм — прямоугольник.
(311549) В параллелограмме  точка
точка  — середина стороны
— середина стороны  . Известно, что
. Известно, что  . Докажите, что данный параллелограмм — прямоугольник.
. Докажите, что данный параллелограмм — прямоугольник.
(314830, 314940, 314982) В параллелограмме  диагонали
диагонали 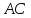 и
и  пересекаются в точке
пересекаются в точке  . Докажите, что площадь параллелограмма
. Докажите, что площадь параллелограмма  в четыре раза больше площади треугольника
в четыре раза больше площади треугольника  .
.
(134939, 314962, 314974) В параллелограмме  диагонали
диагонали 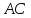 и
и  пересекаются в точке
пересекаются в точке  . Докажите, что площадь параллелограмма
. Докажите, что площадь параллелограмма  в четыре раза больше площади треугольника
в четыре раза больше площади треугольника  .
.
(314948, 314949, 314978) В параллелограмме  диагонали
диагонали 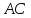 и BD пересекаются в точке
и BD пересекаются в точке  . Докажите, что площадь параллелограмма
. Докажите, что площадь параллелограмма  в четыре раза больше площади треугольника
в четыре раза больше площади треугольника  .
.

(315124) Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
(333026, 339602) Точка  — середина боковой стороны
— середина боковой стороны  трапеции
трапеции  . Докажите, что площадь треугольника
. Докажите, что площадь треугольника  равна половине площади трапеции.
равна половине площади трапеции.
(333105) Точка  — середина боковой стороны
— середина боковой стороны  трапеции
трапеции  . Докажите, что площадь треугольника
. Докажите, что площадь треугольника  равна половине площади трапеции.
равна половине площади трапеции.
(340321) На средней линии трапеции  с основаниями
с основаниями  и
и  выбрали произвольную точку
выбрали произвольную точку  . Докажите, что сумма площадей треугольников
. Докажите, что сумма площадей треугольников  и
и  равна половине площади трапеции.
равна половине площади трапеции.
(351020, 348716) На средней линии трапеции  с основаниями
с основаниями  и
и  выбрали произвольную точку
выбрали произвольную точку  . Докажите, что сумма площадей треугольников
. Докажите, что сумма площадей треугольников  и
и  равна половине площади трапеции.
равна половине площади трапеции.
(340995) Основания  и
и  трапеции
трапеции  равны соответственно
равны соответственно  и
и  ,
,  . Докажите, что треугольники
. Докажите, что треугольники  и
и  подобны.
подобны.
(341131) Основания  и
и  трапеции
трапеции  равны соответственно
равны соответственно  и
и  ,
,  . Докажите, что треугольники
. Докажите, что треугольники  и
и  подобны.
подобны.
(352211) Основания  и
и  трапеции
трапеции  равны соответственно
равны соответственно  и
и  ,
,  . Докажите, что треугольники
. Докажите, что треугольники  и
и  подобны.
подобны.
(348542) Основания  и
и  трапеции
трапеции  равны соответственно
равны соответственно  и
и  ,
,  . Докажите, что треугольники
. Докажите, что треугольники  и
и  подобны.
подобны.
(348674) Основания  и
и  трапеции
трапеции  равны соответственно
равны соответственно  и
и  ,
,  . Докажите, что треугольники
. Докажите, что треугольники  и
и  подобны.
подобны.
(348828) Основания  и
и  трапеции
трапеции  равны соответственно
равны соответственно  и
и  . Докажите, что треугольники
. Докажите, что треугольники  и
и  подобны.
подобны.
(349883) Основания  и
и  трапеции
трапеции  равны соответственно
равны соответственно  и
и  . Докажите, что треугольники
. Докажите, что треугольники  и
и  подобны.
подобны.
(351462) Основания  и
и  трапеции
трапеции  равны соответственно
равны соответственно  и
и  . Докажите, что треугольники
. Докажите, что треугольники  и
и  подобны.
подобны.
(352053) Основания  и
и  трапеции
трапеции  равны соответственно
равны соответственно  и
и  . Докажите, что треугольники
. Докажите, что треугольники  и
и  подобны.
подобны.
(357081, 353559) Биссектрисы углов  и
и  параллелограмма
параллелограмма  пересекаются в точке
пересекаются в точке  лежащей на стороне
лежащей на стороне  . Докажите, что
. Докажите, что 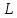 — середина
— середина 
(341027) Биссектрисы углов  и
и  параллелограмма
параллелограмма  пересекаются в точке
пересекаются в точке  стороны
стороны  . Докажите, что
. Докажите, что  — середина
— середина  .
.
(357089) Биссектрисы углов  и
и  параллелограмма
параллелограмма  пересекаются в точке
пересекаются в точке  , лежащей на стороне
, лежащей на стороне  . Докажите, что
. Докажите, что  — середина
— середина  .
.
(357090) Биссектрисы углов  и
и  параллелограмма
параллелограмма  пересекаются в точке
пересекаются в точке  , лежащей на стороне
, лежащей на стороне  . Докажите, что
. Докажите, что  — середина
— середина  .
.
(341722) В выпуклом четырёхугольнике  углы
углы  и
и  равны. Докажите, что углы
равны. Докажите, что углы  и
и  также равны.
также равны.
(357058) В выпуклом четырёхугольнике  углы
углы  и
и  равны. Докажите, что углы
равны. Докажите, что углы  и
и  также равны.
также равны.
(357059) В выпуклом четырёхугольнике  углы
углы  и
и  равны. Докажите, что углы
равны. Докажите, что углы  и
и  также равны.
также равны.
(350517, 357091) В трапеции  с основаниями
с основаниями  и
и  диагонали пересекаются в точке
диагонали пересекаются в точке  . Докажите, что площади треугольников
. Докажите, что площади треугольников  и
и  равны.
равны.
(349904) Через точку  пересечения диагоналей параллелограмма
пересечения диагоналей параллелограмма  проведена прямая, пересекающая стороны
проведена прямая, пересекающая стороны  и
и  в точках
в точках  и
и  соответственно. Докажите, что
соответственно. Докажите, что  .
.
(351704) Через точку  пересечения диагоналей параллелограмма
пересечения диагоналей параллелограмма  проведена прямая, пересекающая стороны
проведена прямая, пересекающая стороны  и
и  в точках
в точках 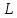 и
и  соответственно. Докажите, что
соответственно. Докажите, что  .
.
(357102) Через точку  пересечения диагоналей параллелограмма
пересечения диагоналей параллелограмма  проведена прямая, пересекающая стороны
проведена прямая, пересекающая стороны  и
и  в точках
в точках  и
и  соответственно. Докажите, что BP=DQ.
соответственно. Докажите, что BP=DQ.
(352949) Через точку  пересечения диагоналей параллелограмма
пересечения диагоналей параллелограмма  проведена прямая, пересекающая стороны
проведена прямая, пересекающая стороны  и
и  в точках
в точках  и
и  соответственно. Докажите, что
соответственно. Докажите, что 
(348892) Сторона  параллелограмма
параллелограмма  вдвое больше стороны
вдвое больше стороны  . Точка
. Точка  — середина стороны
— середина стороны  . Докажите, что
. Докажите, что  — биссектриса угла
— биссектриса угла  .
.
(355303, 355402) Сторона  параллелограмма
параллелограмма  вдвое больше стороны
вдвое больше стороны  . Точка
. Точка  — середина стороны
— середина стороны  . Докажите, что
. Докажите, что  — биссектриса угла
— биссектриса угла  .
.
(355428) Сторона  параллелограмма
параллелограмма  вдвое больше стороны
вдвое больше стороны  . Точка
. Точка 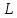 — середина стороны
— середина стороны  . Докажите, что
. Докажите, что  — биссектриса угла
— биссектриса угла  .
.
6







 проведены перпендикуляры
проведены перпендикуляры 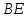 и
и 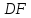 к диагонали
к диагонали 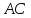 (см. рисунок). Докажите, что
(см. рисунок). Докажите, что 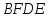 — параллелограмм.
— параллелограмм. 
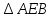 и
и  .
.
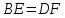 .
. 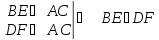 (по признаку параллельности прямых: «если две прямые перпендикулярны третьей прямой, то они параллельны»).
(по признаку параллельности прямых: «если две прямые перпендикулярны третьей прямой, то они параллельны»).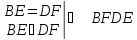 – параллелограмм ( по признаку параллелограмма), ч.т.д.
– параллелограмм ( по признаку параллелограмма), ч.т.д. параллелограмма
параллелограмма  . Точка
. Точка 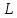 — середина стороны
— середина стороны 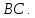 Докажите, что
Докажите, что 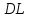 — биссектриса угла
— биссектриса угла 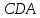 .
.
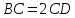 . Т.к.
. Т.к. 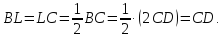 Значит,
Значит, 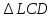 – равнобедренный с основанием
– равнобедренный с основанием 









