ЗАДАНИЕ 25 ОГЭ.
ТРЕУГОЛЬНИКИ И ИХ ЭЛЕМЕНТЫ.
(103; 315022) На стороне 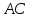 треугольника
треугольника  выбраны точки
выбраны точки 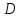 и
и 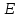 так, что отрезки
так, что отрезки  и
и  равны. Оказалось, что отрезки
равны. Оказалось, что отрезки  и
и 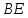 тоже равны. Докажите, что треугольник
тоже равны. Докажите, что треугольник  — равнобедренный.
— равнобедренный.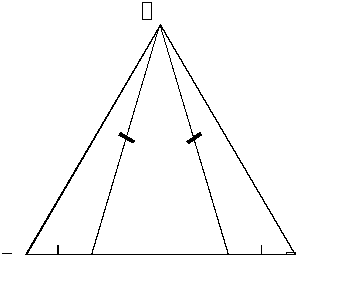
Решение. Треугольник 
 будет равнобедренным, если у него
будет равнобедренным, если у него 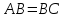 или
или  , поэтому необходимо доказать равенство
, поэтому необходимо доказать равенство 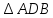 и
и 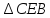 .
.
Рассмотрим сначала  – равнобедренный
– равнобедренный 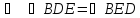 по свойству равнобедренного треугольника. Тогда
по свойству равнобедренного треугольника. Тогда 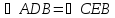 – по свойству смежных углов (если два угла равны, то смежные с ними углы тоже равны).
– по свойству смежных углов (если два угла равны, то смежные с ними углы тоже равны).
Рассмотрим 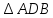 и
и 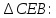
 по I признаку равенства треугольников, следовательно, все соответствующие стороны и углы этих треугольников равны, а конкретно,
по I признаку равенства треугольников, следовательно, все соответствующие стороны и углы этих треугольников равны, а конкретно, 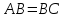 и
и  . Значит,
. Значит, 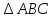 равнобедренный по признаку равнобедренного треугольника, ч.т.д.
равнобедренный по признаку равнобедренного треугольника, ч.т.д.
(340341, 341688) Высоты  и
и  остроугольного треугольника
остроугольного треугольника  пересекаются в точке
пересекаются в точке 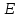 . Докажите, что углы
. Докажите, что углы  и
и  равны.
равны.
Решение. Рассмотрим  и
и 
 по I признаку подобия треугольников, следовательно, стороны у этих треугольников пропорциональны, т.е.
по I признаку подобия треугольников, следовательно, стороны у этих треугольников пропорциональны, т.е.  . Используем следующее свойство пропорции: в верной пропорции, все члены которой отличны от нуля, можно менять местами её крайние и средние члены. Поменяем местами средние члены пропорции, получим:
. Используем следующее свойство пропорции: в верной пропорции, все члены которой отличны от нуля, можно менять местами её крайние и средние члены. Поменяем местами средние члены пропорции, получим:  .
.
Рассмотрим  и
и 
по II признаку подобия треугольников. Значит, по определению подобных треугольников, все соответствующие углы этих треугольников равны, т.е.  , ч.т.д.
, ч.т.д.
(340854, 340243) В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
Решение. Рассмотрим  и
и 
 по I признаку подобия треугольников, следовательно, все соответствующие стороны этих треугольников пропорциональны, т.е.
по I признаку подобия треугольников, следовательно, все соответствующие стороны этих треугольников пропорциональны, т.е.  . Используя свойство пропорции, поменяем местами средние члены пропорции:
. Используя свойство пропорции, поменяем местами средние члены пропорции: 
Рассмотрим  и
и 
по II признаку подобия треугольников, ч.т.д.
(340880) В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.
Решение. Рассмотрим  и
и 
 по I признаку подобия треугольников, следовательно все соответствующие стороны этих треугольников пропорциональны, т.е.
по I признаку подобия треугольников, следовательно все соответствующие стороны этих треугольников пропорциональны, т.е.  . По свойству пропорции:
. По свойству пропорции:  .
.
Рассмотрим  и
и 
по II признаку подобия треугольников  , а значит, и
, а значит, и  , ч.т.д.
, ч.т.д.
(340906) Окружности с центрами в точках E и F пересекаются в точках C и D, причём точки E и F лежат по одну сторону от прямой CD. Докажите, что CD⊥ EF.
Решение. Рассмотрим  и
и 
по III признаку равенства треугольников, значит,  по свойству смежных углов (если два угла равны, то смежные с ними углы тоже равны).
по свойству смежных углов (если два угла равны, то смежные с ними углы тоже равны).
 – равнобедренный (
– равнобедренный ( ),
),  в этом треугольнике является биссектрисой т.к.
в этом треугольнике является биссектрисой т.к.  , значит, по свойству равнобедренного треугольника,
, значит, по свойству равнобедренного треугольника,  является и медианой, и высотой. По определению высоты
является и медианой, и высотой. По определению высоты  , ч.т.д.
, ч.т.д.
(129; 314856) В равностороннем треугольнике ABC точки M, N, K— середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
Решение. Треугольник равносторонний, значит,  .
.  – средние линии треугольника
– средние линии треугольника  (т.к. они соединяют середины двух сторон). По свойству средней линии треугольника . Правые части у этих равенств равны, значит, равны и левые части, т.е.
(т.к. они соединяют середины двух сторон). По свойству средней линии треугольника . Правые части у этих равенств равны, значит, равны и левые части, т.е.  . В
. В  все три стороны равны, значит, он равносторонний, ч.т.д.
все три стороны равны, значит, он равносторонний, ч.т.д.
(311561) На стороне 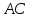 треугольника
треугольника  отмечены точки
отмечены точки 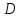 и
и 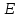 так, что
так, что  . Докажите, что если
. Докажите, что если  , то
, то 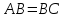 .
.
Решение. В этой задаче рисунок не прилагается, поэтому расположение точек 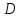 и
и 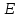 может быть в двух вариантах. Рассмотрим каждый из них.
может быть в двух вариантах. Рассмотрим каждый из них.
I. Пусть точка 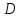 лежит между точками
лежит между точками  и
и 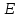 , как показано на рисунке. Тогда
, как показано на рисунке. Тогда  равнобедренный, следовательно, по свойству равнобедренного треугольника,
равнобедренный, следовательно, по свойству равнобедренного треугольника,  . Значит, и
. Значит, и 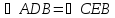 по свойству смежных углов.
по свойству смежных углов.  по I признаку равенства треугольников , следовательно, все соответствующие стороны и углы этих треугольников равны, т.е.
по I признаку равенства треугольников , следовательно, все соответствующие стороны и углы этих треугольников равны, т.е. 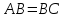 , ч.т.д.
, ч.т.д.
II. Пусть точка 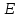 лежит между точками
лежит между точками  и
и 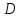 , как показано на рисунке. Тогда, докажем равенство отрезков
, как показано на рисунке. Тогда, докажем равенство отрезков  и
и 
Тогда  равнобедренный, следовательно, по свойству равнобедренного треугольника,
равнобедренный, следовательно, по свойству равнобедренного треугольника,  . Значит, и
. Значит, и  по свойству смежных углов.
по свойству смежных углов.  по I признаку равенства треугольников , следовательно, все соответствующие стороны и углы этих треугольников равны, т.е.
по I признаку равенства треугольников , следовательно, все соответствующие стороны и углы этих треугольников равны, т.е. 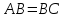 , ч.т.д.
, ч.т.д.
(311567) На медиане  треугольника
треугольника  отмечена точка
отмечена точка 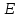 . Докажите, что если
. Докажите, что если  , то
, то  .
.
Решение. Т.к.  , то
, то  – равнобедренный,
– равнобедренный,  в нём является медианой, следовательно, по свойству равнобедренного треугольника, она является и биссектрисой, и высотой. Значит,
в нём является медианой, следовательно, по свойству равнобедренного треугольника, она является и биссектрисой, и высотой. Значит,  и, очевидно,
и, очевидно,  . В
. В  является и медианой, и высотой, значит, этот треугольник равнобедренный, т.е.
является и медианой, и высотой, значит, этот треугольник равнобедренный, т.е.  ч.т.д.
ч.т.д.
(311602) Докажите, что биссектрисы углов при основании равнобедренного треугольника равны.
Решение. 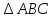 – равнобедренный, значит,
– равнобедренный, значит,  (по свойству равнобедренного треугольника).
(по свойству равнобедренного треугольника).
 и
и  – биссектрисы углов
– биссектрисы углов  и
и  соответственно, поэтому,
соответственно, поэтому,  и
и  . Т.к.
. Т.к.  , то
, то
Рассмотрим  и
и 
по II признаку равенства треугольников. Значит, все соответствующие углы и стороны этих треугольников равны, т.е.  , ч.т.д.
, ч.т.д.
(311605) Два равносторонних треугольника имеют общую вершину. Докажите, что отмеченные на рисунке отрезки AB и CD равны.
Решение. Рассмотрим  и
и 

Рассмотрим  и
и  .
.
по I признаку равенства треугольников, значит,  , ч.т.д.
, ч.т.д.
(311606) Два равных прямоугольника имеют общую вершину O (см. рис.). Докажите, что площади треугольников AOK и COM равны.
Решение.
 как стороны равных прямоугольников.
как стороны равных прямоугольников.
. Используя формулу приведения  , получаем, что . Значит,
, получаем, что . Значит,
 , ч.т.д.
, ч.т.д.
(311665) Докажите, что у равных треугольников ABC и A1B1C1 биссектрисы, проведённые из вершин A и A1, равны.
Решение. Т.к. треугольники равны, то все соответствующие стороны и углы этих треугольников равны, т.е.  . Т.к.
. Т.к.  и
и  – биссектрисы равных углов
– биссектрисы равных углов  и
и  , то они делят углы на равные части, т.е.
, то они делят углы на равные части, т.е.
.
Рассмотрим  и
и 
по II признаку равенства треугольников, следовательно,  , ч.т.д.
, ч.т.д.
(311669) В треугольнике  угол
угол  равен 36°,
равен 36°, 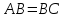 ,
,  — биссектриса. Докажите, что треугольник
— биссектриса. Докажите, что треугольник  — равнобедренный.
— равнобедренный.
Решение. Т.к.  – равнобедренный, то
– равнобедренный, то  . Значит,
. Значит,
Т.к.  — биссектриса
— биссектриса  , то . Значит,
, то . Значит,  , поэтому
, поэтому  – равнобедренный, ч.т.д.
– равнобедренный, ч.т.д.
(311969) Окружность касается стороны  треугольника
треугольника  , у которого
, у которого  и продолжений его сторон
и продолжений его сторон 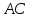 и
и  за точки
за точки  и
и  соответственно. Докажите, что периметр треугольника
соответственно. Докажите, что периметр треугольника  равен диаметру этой окружности.
равен диаметру этой окружности.
Решение. Продолжения сторон  и
и  касаются окружности в точках
касаются окружности в точках  и
и  соответственно, сторона
соответственно, сторона  касается окружности в точке
касается окружности в точке  . По свойству касательных, они составляют с радиусом, проведённым в точку касания, прямой угол. Значит, . Тогда четырёхугольник
. По свойству касательных, они составляют с радиусом, проведённым в точку касания, прямой угол. Значит, . Тогда четырёхугольник  является квадратом (
является квадратом ( ). По свойству отрезков касательных, пересекающихся в одной точке,
). По свойству отрезков касательных, пересекающихся в одной точке,  и
и  . Значит,
. Значит,  . Запишем формулу периметра треугольника
. Запишем формулу периметра треугольника 
. Итак, периметр треугольника  равен диаметру окружности, касающейся стороны
равен диаметру окружности, касающейся стороны  и продолжения сторон
и продолжения сторон  и
и  , ч.т.д.
, ч.т.д.
(315085) На стороне 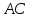 треугольника
треугольника  выбраны точки
выбраны точки 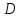 и
и 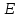 так, что отрезки
так, что отрезки  и
и  равны (см. рисунок). Оказалось, что углы
равны (см. рисунок). Оказалось, что углы  и
и  тоже равны. Докажите, что треугольник
тоже равны. Докажите, что треугольник  — равнобедренный.
— равнобедренный.
Решение. Т.к. 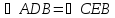 , то
, то  по свойству смежных углов (если два угла равны, то смежные с ними углы тоже равны). Тогда
по свойству смежных углов (если два угла равны, то смежные с ними углы тоже равны). Тогда  – равнобедренный, следовательно,
– равнобедренный, следовательно,  .
.
Рассмотрим 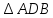 и
и 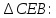
по I признаку равенства треугольников. Значит, все соответствующие стороны и углы этих треугольников равны, т.е. 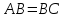 и
и 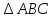 – равнобедренный, ч.т.д.
– равнобедренный, ч.т.д.
(316334) В остроугольном треугольнике  угол
угол  равен 60° . Докажите, что точки
равен 60° . Докажите, что точки  центр описанной окружности треугольника
центр описанной окружности треугольника  и центр вписанной окружности треугольника
и центр вписанной окружности треугольника  лежат на одной окружности.
лежат на одной окружности.
Решение. Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам этого треугольника – точка  ,
,  – радиусы этой окружности. Значит,
– радиусы этой окружности. Значит,  – вписанный в эту окружность, а
– вписанный в эту окружность, а  – центральный угол этой окружности. По свойству вписанных в окружность углов, .
– центральный угол этой окружности. По свойству вписанных в окружность углов, .
Центром окружности, вписанной в треугольник, является точка пересечения биссектрис углов треугольника – точка  ,
,  – биссектрисы углов
– биссектрисы углов  и
и  , значит,
, значит,  и
и  . По сумме углов треугольника, . Из треугольника
. По сумме углов треугольника, . Из треугольника  по сумме углов треугольника . Значит, . Итак, . Значит, равные углы опираются на одну и ту же хорду
по сумме углов треугольника . Значит, . Итак, . Значит, равные углы опираются на одну и ту же хорду 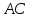 , поэтому они являются вписанными, т.е. точки
, поэтому они являются вписанными, т.е. точки  лежат на одной окружности, ч.т.д.
лежат на одной окружности, ч.т.д.
(333348; 349266) Известно, что около четырёхугольника  можно описать окружность и что продолжения сторон
можно описать окружность и что продолжения сторон  и
и  четырёхугольника пересекаются в точке
четырёхугольника пересекаются в точке  . Докажите, что треугольники
. Докажите, что треугольники  и
и  подобны.
подобны.
Решение. Т.к. окружность описана около четырёхугольника  , то
, то  – как вписанные углы, опирающиеся на одну дугу
– как вписанные углы, опирающиеся на одну дугу  ;
;  – как вписанные углы, опирающиеся на одну дугу
– как вписанные углы, опирающиеся на одну дугу  .
.  – смежный с
– смежный с  , значит, по свойству смежных углов, (из
, значит, по свойству смежных углов, (из  по сумме углов треугольника).
по сумме углов треугольника).
Рассмотрим  и
и 
по I признаку подобия треугольников, ч.т.д.
(339384) Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
Решение.
Т.к.  – медиана треугольника, то она делит сторону
– медиана треугольника, то она делит сторону 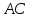 пополам, т.е.
пополам, т.е.  . – по свойству смежных углов. Тогда по формуле приведения . Сторона
. – по свойству смежных углов. Тогда по формуле приведения . Сторона  – общая. Значит,
– общая. Значит,  , ч.т.д.
, ч.т.д.
ЗАДАЧИ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
(357100) В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
(357101, 350829) В треугольнике ABC с тупым углом BAC проведены высоты BB1 и CC1. Докажите, что треугольники AB1C1 и ABC подобны.
(315008) В равнобедренном треугольнике ABC (АВ = ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
(315030) В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
(315051) В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
(311773) В остроугольном треугольнике ABC угол B равен 60°. Докажите, что точки A, C, центр описанной окружности треугольника ABC и точка пересечения высот треугольника ABC лежат на одной окружности.
(316244; 311829) В остроугольном треугольнике ABC точки A, C, центр описанной окружности O и центр вписанной окружности I лежат на одной окружности. Докажите, что угол ABC равен 60°.
(311861; 316271) В остроугольном треугольнике ABC, точки A, C, центр описанной окружности O и точка пересечения высот H лежат на одной окружности. Докажите, что угол ABC равен 60°.
(316297) В остроугольном треугольнике ABC точки A, C, точка пересечения высот H и центр вписанной окружности I лежат на одной окружности. Докажите, что угол ABC равен 60°
(315062) На стороне 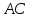 треугольника
треугольника  выбраны точки
выбраны точки 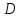 и
и 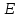 так, что углы
так, что углы  и
и  равны (см. рисунок). Оказалось, что отрезки
равны (см. рисунок). Оказалось, что отрезки  и
и  тоже равны. Докажите, что треугольник
тоже равны. Докажите, что треугольник  — равнобедренный.
— равнобедренный.
(315119) На стороне 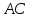 треугольника
треугольника  выбраны точки
выбраны точки 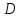 и
и 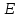 так, что отрезки
так, что отрезки  и
и  равны (см. рисунок). Оказалось, что углы
равны (см. рисунок). Оказалось, что углы  и
и  тоже равны. Докажите, что треугольник
тоже равны. Докажите, что треугольник  — равнобедренный.
— равнобедренный.
(353162) В остроугольном треугольнике ABC проведены высоты BB1 и CC1. Докажите, что углы BB1C1 и BCC1 равны.
(357060) В остроугольном треугольнике ABC проведены высоты AA1 и BB1. Докажите, что углы AA1B1 и ABB1 равны.
(348485) В остроугольном треугольнике ABC проведены высоты AA1 и CC1. Докажите, что углы CC1A1 и CAA1 равны.
(351134) В остроугольном треугольнике ABC проведены высоты AA1 и BB1. Докажите, что углы BAA1 и BB1A1 равны.
(352415) В остроугольном треугольнике ABC проведены высоты AA1 и CC1. Докажите, что углы AA1C1 и ACC1 равны.
(353001) В остроугольном треугольнике ABC проведены высоты BB1 и CC1. Докажите, что углы CC1B и CBB1 равны.
3







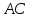 треугольника
треугольника  выбраны точки
выбраны точки 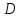 и
и 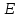 так, что отрезки
так, что отрезки  и
и  равны. Оказалось, что отрезки
равны. Оказалось, что отрезки  и
и 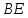 тоже равны. Докажите, что треугольник
тоже равны. Докажите, что треугольник 
 будет равнобедренным, если у него
будет равнобедренным, если у него 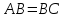 или
или  , поэтому необходимо доказать равенство
, поэтому необходимо доказать равенство 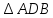 и
и 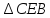 .
.  – равнобедренный
– равнобедренный 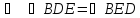 по свойству равнобедренного треугольника. Тогда
по свойству равнобедренного треугольника. Тогда 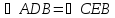 – по свойству смежных углов (если два угла равны, то смежные с ними углы тоже равны).
– по свойству смежных углов (если два угла равны, то смежные с ними углы тоже равны). 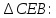
 по I признаку равенства треугольников, следовательно, все соответствующие стороны и углы этих треугольников равны, а конкретно,
по I признаку равенства треугольников, следовательно, все соответствующие стороны и углы этих треугольников равны, а конкретно, 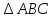 равнобедренный по признаку равнобедренного треугольника, ч.т.д.
равнобедренный по признаку равнобедренного треугольника, ч.т.д.