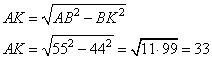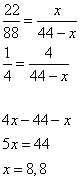СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 30.07.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 13.06.2025 12:11

ШИБАЕВА ОЛЬГА ВЛАДИМИРОВНА
УЧИТЕЛЬ МАТЕМАТИКИ
44 года
Местоположение
РОССИЯ,
Специализация
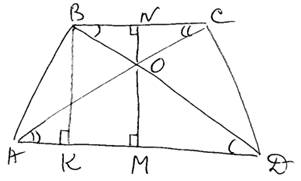
Задание 26 из огэ
© 2024, ШИБАЕВА ОЛЬГА ВЛАДИМИРОВНА 82 0