Вариант 1 10. Задачи с прикладным содержанием
1. Мотоциклист, движущийся по городу со скоростью v0=57 км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением 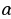 = 12 км/ч2 . Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением S = v0t +
= 12 км/ч2 . Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением S = v0t +  . Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
2. Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: I = 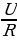 , где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 2,5 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.
, где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 2,5 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.
3. Груз массой 0,38 кг колеблется на пружине. Его скорость v меняется по закону v = v0 cos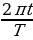 , где
, где  — время с момента начала колебаний, T = 2 с — период колебаний, v0 = 2 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E =
— время с момента начала колебаний, T = 2 с — период колебаний, v0 = 2 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = 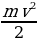 где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 57 секунд после начала колебаний. Ответ дайте в джоулях.
где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 57 секунд после начала колебаний. Ответ дайте в джоулях.
4. При движении ракеты еe видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону l = l0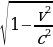 , где l0 = 75 м — длина покоящейся ракеты, c = 3 · 105 км/с — скорость света, а v — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 21 м? Ответ выразите в км/с.
, где l0 = 75 м — длина покоящейся ракеты, c = 3 · 105 км/с — скорость света, а v — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 21 м? Ответ выразите в км/с.
5. Перед отправкой тепловоз издал гудок с частотой f0 = 267 Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону f(v) = 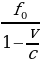 (Гц), где c — скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 3 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.
(Гц), где c — скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 3 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.
6. Некоторая компания продает свою продукцию по цене p = 600 руб. за единицу, переменные затраты на производство одной единицы продукции составляют v = 400 руб., постоянные расходы предприятия f = 600000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле π(q) = q(p-v) – f. Определите месячный объем производства q(единиц продукции), при котором месячная операционная прибыль предприятия будет равна 500000 руб.
7. Плоский замкнутый контур площадью S = 0,5 м2 находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой  , где
, где 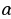 – острый угол между направлением магнитного поля и перпендикуляром к контуру,
– острый угол между направлением магнитного поля и перпендикуляром к контуру,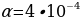 Тл/с – постоянная, S – площадь замкнутого контура, находящегося в магнитном поле (в м2). При каком минимальном угле
Тл/с – постоянная, S – площадь замкнутого контура, находящегося в магнитном поле (в м2). При каком минимальном угле 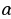 (в градусах) ЭДС индукции не будет превышать 10-4 В?
(в градусах) ЭДС индукции не будет превышать 10-4 В?
8. Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону U = U0cos(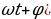 , где
, где  — время в секундах, амплитуда U0= 2 В, частота
— время в секундах, амплитуда U0= 2 В, частота 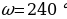 /с, фаза
/с, фаза 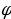 = - 1200. Датчик настроен так, что если напряжение в нем не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
= - 1200. Датчик настроен так, что если напряжение в нем не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
9. Опорные башмаки шагающего экскаватора, имеющего массу m = 1400 тонн представляют собой две пустотелые балки длиной l = 14 метров и шириной 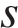 метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой p =
метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой p =  , где m — масса экскаватора (в тоннах), l — длина балок в метрах,
, где m — масса экскаватора (в тоннах), l — длина балок в метрах, 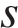 — ширина балок в метрах, g — ускорение свободного падения (считайте g = 10 м/с2). Определите наименьшую возможную ширину опорных балок, если известно, что давление p не должно превышать 250 кПа. Ответ выразите в метрах.
— ширина балок в метрах, g — ускорение свободного падения (считайте g = 10 м/с2). Определите наименьшую возможную ширину опорных балок, если известно, что давление p не должно превышать 250 кПа. Ответ выразите в метрах.
10. Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a = 5000 км/ч2. Скорость вычисляется по формуле 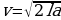 , где l — пройденный автомобилем путь. Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 100 км/ч.
, где l — пройденный автомобилем путь. Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 100 км/ч.
Вариант 2 10. Задачи с прикладным содержанием
1. Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: I = 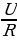 , где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 2,5 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.
, где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 2,5 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.
2. При адиабатическом процессе для идеального газа выполняется закон pVk = 105 Па м5, где p – давление в газе в паскалях, V – объем газа в кубических метрах, k =
м5, где p – давление в газе в паскалях, V – объем газа в кубических метрах, k = 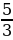 . Найдите, какой объём V (в куб. м) будет занимать газ при давлении p, равном 3,2 · 106 Па.
. Найдите, какой объём V (в куб. м) будет занимать газ при давлении p, равном 3,2 · 106 Па.
3. При адиабатическом процессе для идеального газа выполняется закон pVk = 7,29 ·107 Па м5, где p – давление в газе в паскалях, V – объем газа в кубических метрах, k =
м5, где p – давление в газе в паскалях, V – объем газа в кубических метрах, k = 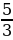 . Найдите, какой объём V (в куб. м) будет занимать газ при давлении p , равном 3 · 105Па.
. Найдите, какой объём V (в куб. м) будет занимать газ при давлении p , равном 3 · 105Па.
4. Для сматывания кабеля на заводе используют лебёдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону 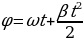 , где t — время в минутах,
, где t — время в минутах, 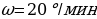 — начальная угловая скорость вращения катушки, а
— начальная угловая скорость вращения катушки, а 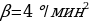 — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки
— угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки 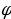 достигнет12000. Определите время после начала работы лебёдки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.
достигнет12000. Определите время после начала работы лебёдки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.
5. При движении ракеты еe видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону 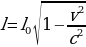 , где
, где 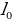 = 5 м – длина покоящейся ракеты, c = 3·105 км/с – скорость света, а
= 5 м – длина покоящейся ракеты, c = 3·105 км/с – скорость света, а 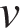 – скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 4 м? Ответ выразите в км/с.
– скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 4 м? Ответ выразите в км/с.
6. Груз массой 0,4 кг колеблется на пружине. Его скорость v меняется по закону v = v0 sin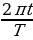 , где t — время с момента начала колебаний, T = 8с — период колебаний,
, где t — время с момента начала колебаний, T = 8с — период колебаний, 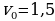 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E =
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = 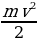 где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 7 секунд после начала колебаний. Ответ дайте в джоулях.
где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 7 секунд после начала колебаний. Ответ дайте в джоулях.
7. Груз массой 0,43 кг колеблется на пружине. Его скорость v меняется по закону v = v0 sin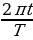 , где t — время с момента начала колебаний, T = 18 с — период колебаний,
, где t — время с момента начала колебаний, T = 18 с — период колебаний, 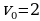 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E =
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = 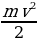 где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 6 секунд после начала колебаний. Ответ дайте в джоулях.
где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 6 секунд после начала колебаний. Ответ дайте в джоулях.
8. Деталью некоторого прибора является квадратная рамка с намотанным на неё проводом, через который пропущен постоянный ток. Рамка помещена в однородное магнитное поле так, что она может вращаться. Момент силы Ампера, стремящейся повернуть рамку, (в Н м) определяется формулой M = NIB
м) определяется формулой M = NIB , где I = 8 Ам — сила тока в рамке, B = 7 · 10-3 Тл — значение индукции магнитного поля,
, где I = 8 Ам — сила тока в рамке, B = 7 · 10-3 Тл — значение индукции магнитного поля, 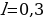 м — размер рамки, N = 250 — число витков провода в рамке,
м — размер рамки, N = 250 — число витков провода в рамке, 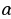 — острый угол между перпендикуляром к рамке и вектором индукции. При каком наименьшем значении угла
— острый угол между перпендикуляром к рамке и вектором индукции. При каком наименьшем значении угла 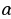 (в градусах) рамка может начать вращаться, если для этого нужно, чтобы раскручивающий момент M был не меньше 0,63 Н·м?
(в градусах) рамка может начать вращаться, если для этого нужно, чтобы раскручивающий момент M был не меньше 0,63 Н·м?
9. В ходе распада радиоактивного изотопа его масса уменьшается по закону m(t) = m0·2-t/T , где m0 – начальная масса изотопа, t – время, прошедшее от начального момента, T – период полураспада. В начальный момент времени масса изотопа 40 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.
10. Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: T(t) = T0 + bt + at2 , где t — время в минутах, T0 = 1380 К, а = −15 К/мин2, b= 165 К/мин. Известно, что при температуре нагревателя свыше 1800 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
Вариант 3 10. Задачи с прикладным содержанием
1. Высота над землей подброшенного вверх мяча меняется по закону h(t) = 2 + 9t – 5t2 , где h — высота в метрах,  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте более 6 метров?
— время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте более 6 метров?
2. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой 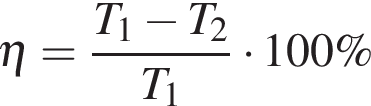 , где T1 — температура нагревателя (в градусах Кельвина), T2 — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя T1 КПД этого двигателя будет не меньше 25%, если температура холодильника T2 = 276 К? Ответ выразите в градусах Кельвина.
, где T1 — температура нагревателя (в градусах Кельвина), T2 — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя T1 КПД этого двигателя будет не меньше 25%, если температура холодильника T2 = 276 К? Ответ выразите в градусах Кельвина.
3. По закону Ома для полной цепи сила тока, измеряемая в амперах, равна I = 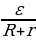 , где
, где 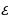 — ЭДС источника (в вольтах), r = 1 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания Iкз =
— ЭДС источника (в вольтах), r = 1 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания Iкз = 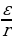 ? (Ответ выразите в омах.)
? (Ответ выразите в омах.)
4. Груз массой 0,8 кг колеблется на пружине. Его скорость v меняется по закону v = v0 cos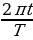 , где
, где  — время с момента начала колебаний, T = 2 с — период колебаний,
— время с момента начала колебаний, T = 2 с — период колебаний, 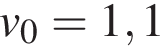 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E =
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = 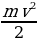 , где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 32 секунды после начала колебаний. Ответ дайте в джоулях.
, где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 32 секунды после начала колебаний. Ответ дайте в джоулях.
5. Груз массой 0,4 кг колеблется на пружине. Его скорость v меняется по закону v = v0 cos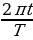 , где
, где  — время с момента начала колебаний, T = 2 с — период колебаний,
— время с момента начала колебаний, T = 2 с — период колебаний, 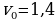 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E =
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = 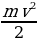 , где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 13 секунд после начала колебаний. Ответ дайте в джоулях.
, где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 13 секунд после начала колебаний. Ответ дайте в джоулях.
6.Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой 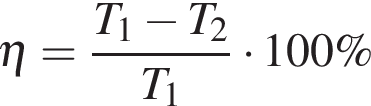 , где T1 – температура нагревателя (в градусах Кельвина), T2 – температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя T1 КПД этого двигателя будет не меньше 15%, если температура холодильника N2 = 340 К? Ответ выразите в градусах Кельвина.
, где T1 – температура нагревателя (в градусах Кельвина), T2 – температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя T1 КПД этого двигателя будет не меньше 15%, если температура холодильника N2 = 340 К? Ответ выразите в градусах Кельвина.
7. Некоторая компания продает свою продукцию по цене p = 500 руб. за единицу, переменные затраты на производство одной единицы продукции составляют v = 300 руб., постоянные расходы предприятия f = 700000 руб. месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле π (q) = q(p - v) – f. Определите месячный объем производства q(единиц продукции), при котором месячная операционная прибыль предприятия будет равна 300000 руб.
8. При нормальном падении света с длиной волны  нм на дифракционную решётку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол
нм на дифракционную решётку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол 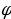 (отсчитываемый от перпендикуляра к решетке), под которым наблюдается максимум, и номер максимума
(отсчитываемый от перпендикуляра к решетке), под которым наблюдается максимум, и номер максимума 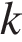 связаны соотношением
связаны соотношением 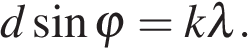 Под каким минимальным углом
Под каким минимальным углом 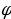 (в градусах) можно наблюдать второй максимум на решётке с периодом, не превосходящим 1600 нм?
(в градусах) можно наблюдать второй максимум на решётке с периодом, не превосходящим 1600 нм?
9. Автомобиль, движущийся в начальный момент времени со скоростью v0 = 30 м/с, начал торможение с постоянным ускорением 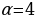 м/с2. За t секунд после начала торможения он прошел путь S = v0t -
м/с2. За t секунд после начала торможения он прошел путь S = v0t - 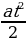 (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 112 метров. Ответ выразите в секундах.
(м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 112 метров. Ответ выразите в секундах.
10. Груз массой 0,16 кг колеблется на пружине. Его скорость v меняется по закону v = v0 cos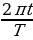 где
где  — время с момента начала колебаний, T = 2 с — период колебаний, v0 = 1,5 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E =
— время с момента начала колебаний, T = 2 с — период колебаний, v0 = 1,5 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = 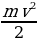 , где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 2 секунды после начала колебаний. Ответ дайте в джоулях.
, где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 2 секунды после начала колебаний. Ответ дайте в джоулях.
Вариант 4 10. Задачи с прикладным содержанием
1. Перед отправкой тепловоз издал гудок с частотой f0 = 440 Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону f(v) = 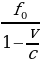 (Гц), где
(Гц), где  – скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а
– скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а 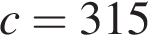 м/с. Ответ выразите в м/с.
м/с. Ответ выразите в м/с.
2. При движении ракеты еe видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону 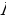 =
=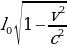 , где
, где 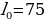 м — длина покоящейся ракеты, c = 3
м — длина покоящейся ракеты, c = 3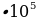 км/с — скорость света, а v — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 21 м? Ответ выразите в км/с.
км/с — скорость света, а v — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 21 м? Ответ выразите в км/с.
3. Груз массой 0,8 кг колеблется на пружине. Его скорость v меняется по закону v = v0 sin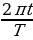 , где t — время с момента начала колебаний, T = 12 с — период колебаний,
, где t — время с момента начала колебаний, T = 12 с — период колебаний,  м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E =
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = 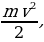 где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях.
где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях.
4. В телевизоре ёмкость высоковольтного конденсатора C = 3·10-6 Ф. Параллельно с конденсатором подключён резистор с сопротивлением R = 2·106 Ом. Во время работы телевизора напряжение на конденсаторе U0= 30 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением t = 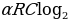
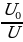 (с), где
(с), где 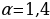 — постоянная. Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло 25,2 с. Ответ дайте в киловольтах.
— постоянная. Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло 25,2 с. Ответ дайте в киловольтах.
5. Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением 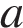 км/ч 2 . Скорость вычисляется по формуле v =
км/ч 2 . Скорость вычисляется по формуле v = 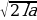 , где
, где 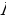 — пройденный автомобилем путь. Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 1,1 километра, приобрести скорость 110 км/ч. Ответ выразите в км/ч2 .
— пройденный автомобилем путь. Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 1,1 километра, приобрести скорость 110 км/ч. Ответ выразите в км/ч2 .
6. Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением
a = 4500км/ч2. Скорость 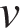 (в км/ч) вычисляется по формуле v =
(в км/ч) вычисляется по формуле v = 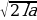 , где
, где 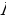 — пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 90 км/ч.
— пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 90 км/ч.
7. Высота над землёй подброшенного вверх мяча меняется по закону h(t) = 2t + 9t – 5t2, где 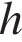 — высота в метрах,
— высота в метрах,  — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте более 6 метров?
— время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте более 6 метров?
8. Очень лёгкий заряженный металлический шарик зарядом q = 8 • 10-6 Кл скатывается по гладкой наклонной плоскости. В момент, когда его скорость составляет  м/с, на него начинает действовать постоянное магнитное поле, вектор индукции B которого лежит в той же плоскости и составляет угол
м/с, на него начинает действовать постоянное магнитное поле, вектор индукции B которого лежит в той же плоскости и составляет угол  с направлением движения шарика. Значение индукции поля B = 5·10-3 Тл. При этом на шарик действует сила Лоренца, равная Fл = q
с направлением движения шарика. Значение индукции поля B = 5·10-3 Тл. При этом на шарик действует сила Лоренца, равная Fл = q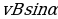 (Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла
(Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла 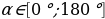 шарик отрывается от поверхности, если для этого нужно, чтобы сила FЛ была не менее чем 6 · 10-8 Н? Ответ дайте в градусах.
шарик отрывается от поверхности, если для этого нужно, чтобы сила FЛ была не менее чем 6 · 10-8 Н? Ответ дайте в градусах.
9. Расстояние от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле l = 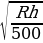 , где R = 6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 5,6 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 10,4 километров?
, где R = 6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 5,6 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 10,4 километров?
10. Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P(в паскалях), оказываемое навесом и колонной на опору, определяется по формуле Р = 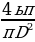 , где m = 2400 кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения g = 10 м/с2, а π = 3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 800 000 Па. Ответ выразите в метрах.
, где m = 2400 кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения g = 10 м/с2, а π = 3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 800 000 Па. Ответ выразите в метрах.
Вариант 5 10. Задачи с прикладным содержанием
1. Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону U = U0sin(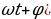 , где
, где  – время в секундах, амплитуда U0 = 2 В, частота
– время в секундах, амплитуда U0 = 2 В, частота 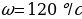 /с, фаза
/с, фаза 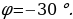 Датчик настроен так, что если напряжение в нем не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
Датчик настроен так, что если напряжение в нем не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
2. Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле P = 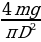 , где m = 1200 кг – общая масса навеса и колонны, D – диаметр колонны (в метрах). Считая ускорение свободного падения g = 10 м/с2, а π = 3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400 000 Па. Ответ выразите в метрах.
, где m = 1200 кг – общая масса навеса и колонны, D – диаметр колонны (в метрах). Считая ускорение свободного падения g = 10 м/с2, а π = 3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400 000 Па. Ответ выразите в метрах.
3. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной 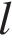 км с постоянным ускорением
км с постоянным ускорением 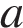 км/ч 2, вычисляется по формуле v =
км/ч 2, вычисляется по формуле v = 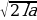 . Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч2.
. Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/ч2.
4. Рейтинг R интернет-магазина вычисляется по формуле R = rпок - 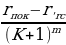 , где m =
, где m = 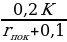 , rпок — средняя оценка магазина покупателями, rэкс — оценка магазина, данная экспертами, K — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 7, их средняя оценка равна 0,32, а оценка экспертов равна 0,22.
, rпок — средняя оценка магазина покупателями, rэкс — оценка магазина, данная экспертами, K — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 7, их средняя оценка равна 0,32, а оценка экспертов равна 0,22.
5. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: Fa = 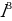 , где
, где 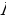 – длина ребра куба в метрах,
– длина ребра куба в метрах, 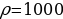 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах.
кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах.
6. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: : Fa = 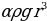 , где
, где 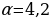 – постоянная,
– постоянная,  – радиус аппарата в метрах,
– радиус аппарата в метрах, 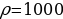 кг/м3 – плотность воды, а
кг/м3 – плотность воды, а 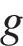 – ускорение свободного падения (считайте
– ускорение свободного падения (считайте 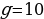 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах.
Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах.
7. После дождя уровень воды в колодце может повыситься. Мальчик измеряет время  падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h = 5t² , где h – расстояние в метрах, t – время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h = 5t² , где h – расстояние в метрах, t – время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
8. Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: T(t) = T0 + bt + at2 , где  – время в минутах, T0=1400 К, a = -10 К/мин2, b = 200 К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
– время в минутах, T0=1400 К, a = -10 К/мин2, b = 200 К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
9. Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой h(t) = -5t² + 18 t , где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров.
10. Рейтинг  интернет-магазина вычисляется по формуле
интернет-магазина вычисляется по формуле
R = rпок - 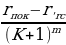 , где m =
, где m = 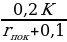 ,
,  — средняя оценка, данная экспертами,
— средняя оценка, данная экспертами,  — средняя оценка, данная покупателями, K — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 24, их средняя оценка равна 0,86, а оценка экспертов равна 0,11.
— средняя оценка, данная покупателями, K — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 24, их средняя оценка равна 0,86, а оценка экспертов равна 0,11.
Вариант 6 10. Задачи с прикладным содержанием
1. Груз массой 0,2 кг колеблется на пружине. Его скорость v меняется по закону v = v0cos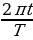 где
где  — время с момента начала колебаний, T = 2с — период колебаний, v0 = 1,8 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E =
— время с момента начала колебаний, T = 2с — период колебаний, v0 = 1,8 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = 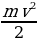 , где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 40 секунд после начала колебаний. Ответ дайте в джоулях.
, где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 40 секунд после начала колебаний. Ответ дайте в джоулях.
2. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: FA = 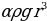 , где
, где 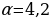 – постоянная,
– постоянная,  – радиус аппарата в метрах,
– радиус аппарата в метрах, 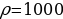 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах.
кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах.
3. Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому P = 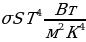 , где Р — мощность излучения звезды (в Ваттах),
, где Р — мощность излучения звезды (в Ваттах),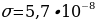 — постоянная, S м
— постоянная, S м — площадь поверхности звезды (в квадратных метрах), а
— площадь поверхности звезды (в квадратных метрах), а 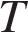 — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна
— температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна 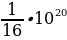 м2, а мощность её излучения равна 9,12 ·1025 Вт. Найдите температуру этой звезды в Кельвинах.
м2, а мощность её излучения равна 9,12 ·1025 Вт. Найдите температуру этой звезды в Кельвинах.
4. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 30 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d2 от линзы до экрана – в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение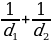 =
= 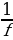 . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чётким. Ответ выразите в сантиметрах.
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чётким. Ответ выразите в сантиметрах.
5. Перед отправкой тепловоз издал гудок с частотой f0 = 440 Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону f(v) = 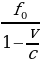 (Гц), где
(Гц), где  – скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.
– скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.
6. По закону Ома для полной цепи сила тока, измеряемая в амперах, равна I = 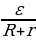 , где
, где 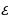 – ЭДС источника (в вольтах), r = 1 Ом – его внутреннее сопротивление, R – сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания Iкз =
– ЭДС источника (в вольтах), r = 1 Ом – его внутреннее сопротивление, R – сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания Iкз = 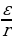 ? (Ответ выразите в омах.)
? (Ответ выразите в омах.)
7. Расстояние (в км) от наблюдателя, находящегося на небольшой высоте h километров над замлей, до наблюдаемой им линии горизонта вычисляется по формуле 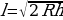 , где R = 6400 (км) — радиус Земли. С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах.
, где R = 6400 (км) — радиус Земли. С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах.
8. Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: I = 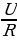 , где U – напряжение в вольтах, R – сопротивление электроприбора в омах. В электросеть включён предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.
, где U – напряжение в вольтах, R – сопротивление электроприбора в омах. В электросеть включён предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.
9. Трактор тащит сани с силой F = 80 кН, направленной под острым углом 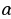 к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 50 м вычисляется по формуле A = FScos
к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 50 м вычисляется по формуле A = FScos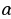 . При каком максимальном угле
. При каком максимальном угле 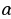 (в градусах) совершенная работа будет не менее 2000 кДж?
(в градусах) совершенная работа будет не менее 2000 кДж?
10. Трактор тащит сани с силой F = 40 кН, направленной под острым углом  к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 200 м вычисляется по формуле A = FScos
к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 200 м вычисляется по формуле A = FScos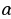 . При каком максимальном угле
. При каком максимальном угле  (в градусах) совершенная работа будет не менее 4000 кДж
(в градусах) совершенная работа будет не менее 4000 кДж
Вариант 7 10. Задачи с прикладным содержанием
1. Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полeта камня описывается формулой у = ах2 + bx , где a = - 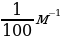 , b =
, b = 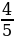 — постоянные параметры, x (м) — смещение камня по горизонтали, y (м) — высота камня над замлей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 14 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
— постоянные параметры, x (м) — смещение камня по горизонтали, y (м) — высота камня над замлей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 14 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
2. Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой h(t) = -5t2 + 18t , где h — высота в метрах,  — время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров.
— время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров.
3. Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой m = 8 кг и радиуса R = 10 см, и двух боковых с массами M = 1 кг и с радиусами R + h. При этом момент инерции катушки относительно оси вращения, выражаемый в кг•см2 , заедается формулой I = 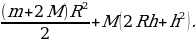 При каком максимальном значении
При каком максимальном значении 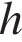 момент инерции катушки не превышает предельного значения 625 кг•см2? Ответ выразите в сантиметрах.
момент инерции катушки не превышает предельного значения 625 кг•см2? Ответ выразите в сантиметрах.
4. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: FА = 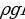 3, где l – длина ребра куба в метрах,
3, где l – длина ребра куба в метрах, 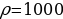 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах.
кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах.
5. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: FA = 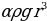 , где
, где 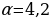 – постоянная,
– постоянная,  – радиус аппарата в метрах,
– радиус аппарата в метрах, 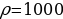 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах.
кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах.
6. Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому Р=σST4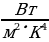 , где Р — мощность излучения звезды (в Ваттах),
, где Р — мощность излучения звезды (в Ваттах),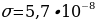 — постоянная, S м2 — площадь поверхности звезды (в квадратных метрах), а
— постоянная, S м2 — площадь поверхности звезды (в квадратных метрах), а 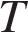 — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна
— температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна 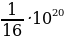 м2, а мощность её излучения равна 9,12 · 1025 Вт. Найдите температуру этой звезды в Кельвинах.
м2, а мощность её излучения равна 9,12 · 1025 Вт. Найдите температуру этой звезды в Кельвинах.
7. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 30 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d2 от линзы до экрана – в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение 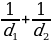 =
= 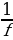 . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чётким. Ответ выразите в сантиметрах.
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чётким. Ответ выразите в сантиметрах.
8. Водолазный колокол, содержащий υ = 2 моля воздуха при давлении p1 = 1,75 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления p2. Работа, совершаемая водой при сжатии воздуха, определяется выражением А = 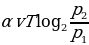 , где
, где 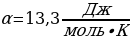 — постоянная, T = 300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15 960 Дж.
— постоянная, T = 300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15 960 Дж.
9. Перед отправкой тепловоз издал гудок с частотой f0 Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону f(v) = 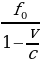 (Гц), где
(Гц), где  – скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.
– скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.
10. Расстояние (в км) от наблюдателя, находящегося на небольшой высоте 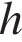 километров над замлей, до наблюдаемой им линии горизонта вычисляется по формуле
километров над замлей, до наблюдаемой им линии горизонта вычисляется по формуле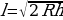 , где R = 6400 (км) — радиус Земли. С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах.
, где R = 6400 (км) — радиус Земли. С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах.
Вариант 8 10. Задачи с прикладным содержанием
1. Зависимость объёма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задается формулой q = 85 – 5p. Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле r(p) = q·p. Определите наибольшую цену p, при которой месячная выручка r(p) составит не менее 360 тыс. руб. Ответ приведите в тыс. руб.
2. Мотоциклист, движущийся по городу со скоростью v0 = 57 км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением 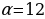 км/ч
км/ч Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением S = v0t -
Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением S = v0t - 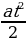 . Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
3. Автомобиль, движущийся в начальный момент времени со скоростью v0 = 20 м/с, начал торможение с постоянным ускорением 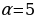 м/с2. За
м/с2. За  – секунд после начала торможения он прошёл путь S = v0t -
– секунд после начала торможения он прошёл путь S = v0t - 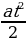 (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.
(м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.
4. Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой m = 8 кг и радиуса R = 10 см, и двух боковых с массами M = 1 кг и с радиусами R + h/ При этом момент инерции катушки относительно оси вращения, выражаемый в кг·см2, даeтся формулой I = 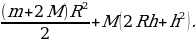 При каком максимальном значении h момент инерции катушки не превышает предельного значения 625 кг·см2? Ответ выразите в сантиметрах.
При каком максимальном значении h момент инерции катушки не превышает предельного значения 625 кг·см2? Ответ выразите в сантиметрах.
5. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: FА = 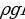 3, где
3, где 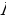 – длина ребра куба в метрах,
– длина ребра куба в метрах, 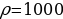 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах.
кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах.
6. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: FA = 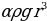 , где
, где 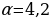 – постоянная,
– постоянная,  – радиус аппарата в метрах,
– радиус аппарата в метрах, 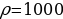 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах.
кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах.
7. Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому Р=σST4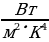 , где P — мощность излучения звезды (в Ваттах),
, где P — мощность излучения звезды (в Ваттах), 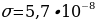 — постоянная, S м2 — площадь поверхности звезды (в квадратных метрах), а T — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна
— постоянная, S м2 — площадь поверхности звезды (в квадратных метрах), а T — температура (в кельвинах). Известно, что площадь поверхности не-которой звезды равна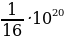 м2, а мощность её излучения равна 9,12 · 1025 Вт. Найдите температуру этой звезды в Кельвинах.
м2, а мощность её излучения равна 9,12 · 1025 Вт. Найдите температуру этой звезды в Кельвинах.
8. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 30 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d2 от линзы до экрана – в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение 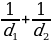 =
= 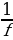 . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чётким. Ответ выразите в сантиметрах.
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чётким. Ответ выразите в сантиметрах.
9. Перед отправкой тепловоз издал гудок с частотой f0 = 440 Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону f(v) = 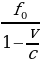 (Гц), где
(Гц), где  – скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.
– скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.
10. По закону Ома для полной цепи сила тока, измеряемая в амперах, равна I = 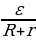 , где
, где 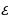 – ЭДС источника (в вольтах), r = 1 Ом – его внутреннее сопротивление, R – сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания Iкз =
– ЭДС источника (в вольтах), r = 1 Ом – его внутреннее сопротивление, R – сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания Iкз = 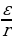 ? (Ответ выразите в омах.)
? (Ответ выразите в омах.)
Вариант 9 10. Задачи с прикладным содержанием
1. Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землeй, до наблюдаемой им линии горизонта вычисляется по формуле 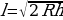 , где R = 6400 (км) — радиус Земли. С какой высоты горизонт виден на расстоянии 28 километров? Ответ выразите в километрах.
, где R = 6400 (км) — радиус Земли. С какой высоты горизонт виден на расстоянии 28 километров? Ответ выразите в километрах.
2. Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полeта камня описывается формулой y = ax2 + bx, где 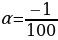 м-1, b = 1 – постоянные параметры, x(m) – смещение камня по горизонтали, y(m) – высота камня над замлей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
м-1, b = 1 – постоянные параметры, x(m) – смещение камня по горизонтали, y(m) – высота камня над замлей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
3. Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: T(t) = T0 + bt + at2 , где  – время в минутах, T0=1400 К, a = -10 К/мин2, b = 200 К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
– время в минутах, T0=1400 К, a = -10 К/мин2, b = 200 К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
4. Для сматывания кабеля на заводе используют лебёдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону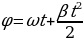 , где t — время в минутах,
, где t — время в минутах, 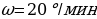 — начальная угловая скорость вращения катушки, а
— начальная угловая скорость вращения катушки, а 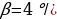 мин2 — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки
мин2 — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки 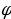 достигнет 12000. Определите время после начала работы лебёдки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.
достигнет 12000. Определите время после начала работы лебёдки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.
5. Мотоциклист, движущийся по городу со скоростью v0 = 57 км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением 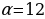 км/ч2. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением S = v0t -
км/ч2. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением S = v0t - 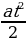 . Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
6. Перед отправкой тепловоз издал гудок с частотой f0 = 440 Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону f(v) = 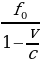 (Гц), где
(Гц), где  – скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.
– скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.
7. Водолазный колокол, содержащий υ = 2 моля воздуха при давлении p1 = 1,75 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления p2. Работа, совершаемая водой при сжатии воздуха, определяется выражением А = 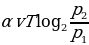 , где
, где 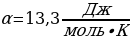 — постоянная, T = 300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15 960 Дж.
— постоянная, T = 300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15 960 Дж.
8. Автомобиль, движущийся в начальный момент времени со скоростью v0 = 20 м/с, начал торможение с постоянным ускорением 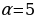 м/с2. За
м/с2. За  – секунд после начала торможения он прошёл путь S = v0t -
– секунд после начала торможения он прошёл путь S = v0t - 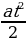 (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.
(м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.
9. Трактор тащит сани с силой F = 80 кН, направленной под острым углом  к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 50 м вычисляется по формуле A = FScos
к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 50 м вычисляется по формуле A = FScos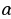 . При каком максимальном угле
. При каком максимальном угле  (в градусах) совершенная работа будет не менее 2000 кДж?
(в градусах) совершенная работа будет не менее 2000 кДж?
10. Трактор тащит сани с силой F = 40 кН, направленной под острым углом  к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 200 м вычисляется по формуле A = FScos
к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 200 м вычисляется по формуле A = FScos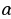 . При каком максимальном угле
. При каком максимальном угле  (в градусах) совершенная работа будет не менее 4000 кДж?
(в градусах) совершенная работа будет не менее 4000 кДж?
Вариант 10 10. Задачи с прикладным содержанием
1. Груз массой 0,8 кг колеблется на пружине. Его скорость v меняется по закону v = v0 cos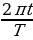 где
где  — время с момента начала колебаний, T = 2 с — период колебаний, v0 = 0,9 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E =
— время с момента начала колебаний, T = 2 с — период колебаний, v0 = 0,9 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = 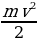 где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 37 секунд после начала колебаний. Ответ дайте в джоулях.
где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 37 секунд после начала колебаний. Ответ дайте в джоулях.
2. После дождя уровень воды в колодце может повыситься. Мальчик измеряет время  падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h = 5t2, где h – расстояние в метрах,
падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h = 5t2, где h – расстояние в метрах,  – время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
– время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
3. Зависимость объёма спроса q (единиц в месяц) на продукцию предприятия – монополиста от цены 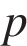 (тыс. руб.) задается формулой q = 100 – 10p. Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле r(p) = q · p. Определите наибольшую цену p, при которой месячная выручка r(p) составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.
(тыс. руб.) задается формулой q = 100 – 10p. Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле r(p) = q · p. Определите наибольшую цену p, при которой месячная выручка r(p) составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.
4. Высота над замлей подброшенного вверх мяча меняется по закону h(t) = 1,6 + 8t – 5t2, где h – высота в метрах,  – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трёх метров?
– время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трёх метров?
5. Если достаточно быстро вращать ведёрко с водой на верёвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведёрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна P = m(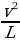 – g), где
– g), где  – масса воды в килограммах,
– масса воды в килограммах, 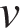 скорость движения ведёрка в м/с, L – длина верёвки в метрах, g – ускорение свободного падения (считайте g = 10 м/с2). С какой наименьшей скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина верёвки равна 40 см? Ответ выразите в м/с.
скорость движения ведёрка в м/с, L – длина верёвки в метрах, g – ускорение свободного падения (считайте g = 10 м/с2). С какой наименьшей скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина верёвки равна 40 см? Ответ выразите в м/с.
6. Трактор тащит сани с силой F = 80 кН, направленной под острым углом  к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 50 м вычисляется по формуле A = FScos
к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 50 м вычисляется по формуле A = FScos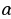 . При каком максимальном угле
. При каком максимальном угле  (в градусах) совершенная работа будет не менее 2000 кДж?
(в градусах) совершенная работа будет не менее 2000 кДж?
7. Трактор тащит сани с силой F = 40 кН, направленной под острым углом  к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 200 м вычисляется по формуле A = FScos
к горизонту. Работа трактора (в килоджоулях) на участке длиной S = 200 м вычисляется по формуле A = FScos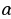 . При каком максимальном угле
. При каком максимальном угле  (в градусах) совершенная работа будет не менее 4000 кДж?
(в градусах) совершенная работа будет не менее 4000 кДж?
8. В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону H(t) = H0 - 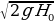 kt +
kt + 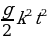 где
где  – время в секундах, прошедшее с момента открытия крана, H0 = 20 – начальная высота столба воды, k =
– время в секундах, прошедшее с момента открытия крана, H0 = 20 – начальная высота столба воды, k = 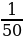 – отношение площадей поперечных сечений крана и бака, а g – ускорение свободного падения (считайте g = 10 м/с
– отношение площадей поперечных сечений крана и бака, а g – ускорение свободного падения (считайте g = 10 м/с ). Через сколько секунд после открытия крана в баке останется четверть первоначального объёма воды?
). Через сколько секунд после открытия крана в баке останется четверть первоначального объёма воды?
9. боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону H(t) = at2 + bt + H0 , где H0 = 4 – начальный уровень воды, 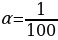 м/мин2, и b = -
м/мин2, и b = - 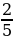 м/мин постоянные,
м/мин постоянные,  – время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.
– время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.
10. Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полeта камня описывается формулой y = ax2 + bx , где a = - 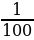 м-1, b = 1 – постоянные параметры, x(м) – смещение камня по горизонтали, y(м) – высота камня над замлей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
м-1, b = 1 – постоянные параметры, x(м) – смещение камня по горизонтали, y(м) – высота камня над замлей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
| 10. Задачи с прикладным содержанием |
| Вариант 1 -
30 -
88 -
0,76 -
28800 -
3,5 -
5500 -
60 -
50 -
2 -
1 | Вариант 2 -
88 -
0,125 -
27 -
20 -
18000 -
0,225 -
0,645 -
30 -
30 -
4 | Вариант 3 -
0,2 -
368 -
4 -
0,484 -
0,392 -
400 -
5000 -
30 -
7 -
0,18 | Вариант 4 -
7 -
28800 -
0,243 -
3,75 -
5500 -
0,9 -
0,2 -
30 -
6 -
0,2 | Вариант 5 -
50 -
0,2 -
5000 -
0,27 -
2 -
2 -
1 -
2 -
2,4 -
0,71 |
| Вариант 6 -
0,324 -
2 -
4000 -
36 -
7 -
4 -
0,00125 -
55 -
60 -
60 | Вариант 7 -
50 -
2.4 -
5 -
2 -
2 -
4000 -
36 -
7 -
7 -
0,00125 | Вариант 8 -
9 -
30 -
2 -
5 -
2 -
2 -
4000 -
36 -
7 -
4 | Вариант 9 -
0,06125 -
90 -
2 -
20 -
30 -
7 -
7 -
2 -
60 -
60 | Вариант 10 -
0,324 -
1 -
6 -
1,2 -
2 -
60 -
60 -
50 -
20 -
90 |







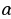 = 12 км/ч2 . Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением S = v0t +
= 12 км/ч2 . Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением S = v0t +  . Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.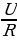 , где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 2,5 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.
, где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 2,5 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.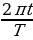 , где
, где 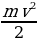 где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 57 секунд после начала колебаний. Ответ дайте в джоулях.
где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 57 секунд после начала колебаний. Ответ дайте в джоулях.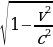 , где l0 = 75 м — длина покоящейся ракеты, c = 3 · 105 км/с — скорость света, а v — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 21 м? Ответ выразите в км/с.
, где l0 = 75 м — длина покоящейся ракеты, c = 3 · 105 км/с — скорость света, а v — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 21 м? Ответ выразите в км/с.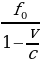 (Гц), где c — скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 3 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.
(Гц), где c — скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 3 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с. , где
, где 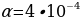 Тл/с – постоянная, S – площадь замкнутого контура, находящегося в магнитном поле (в м2). При каком минимальном угле
Тл/с – постоянная, S – площадь замкнутого контура, находящегося в магнитном поле (в м2). При каком минимальном угле 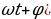 , где
, где 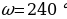 /с, фаза
/с, фаза 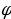 = - 1200. Датчик настроен так, что если напряжение в нем не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
= - 1200. Датчик настроен так, что если напряжение в нем не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть? , где m — масса экскаватора (в тоннах), l — длина балок в метрах,
, где m — масса экскаватора (в тоннах), l — длина балок в метрах, 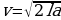 , где l — пройденный автомобилем путь. Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 100 км/ч.
, где l — пройденный автомобилем путь. Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 100 км/ч.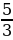 . Найдите, какой объём V (в куб. м) будет занимать газ при давлении p, равном 3,2 · 106 Па.
. Найдите, какой объём V (в куб. м) будет занимать газ при давлении p, равном 3,2 · 106 Па.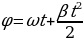 , где t — время в минутах,
, где t — время в минутах, 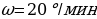 — начальная угловая скорость вращения катушки, а
— начальная угловая скорость вращения катушки, а 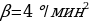 — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки
— угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки 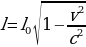 , где
, где 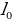 = 5 м – длина покоящейся ракеты, c = 3·105 км/с – скорость света, а
= 5 м – длина покоящейся ракеты, c = 3·105 км/с – скорость света, а 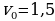 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E =
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = 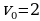 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E =
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E =  , где I = 8 Ам — сила тока в рамке, B = 7 · 10-3 Тл — значение индукции магнитного поля,
, где I = 8 Ам — сила тока в рамке, B = 7 · 10-3 Тл — значение индукции магнитного поля, 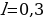 м — размер рамки, N = 250 — число витков провода в рамке,
м — размер рамки, N = 250 — число витков провода в рамке, 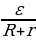 , где
, где 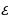 — ЭДС источника (в вольтах), r = 1 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания Iкз =
— ЭДС источника (в вольтах), r = 1 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания Iкз = 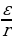 ? (Ответ выразите в омах.)
? (Ответ выразите в омах.)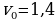 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E =
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле E = 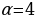 м/с2. За t секунд после начала торможения он прошел путь S = v0t -
м/с2. За t секунд после начала торможения он прошел путь S = v0t - 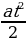 (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 112 метров. Ответ выразите в секундах.
(м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 112 метров. Ответ выразите в секундах.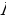 =
=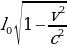 , где
, где 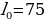 м — длина покоящейся ракеты, c = 3
м — длина покоящейся ракеты, c = 3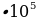 км/с — скорость света, а v — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 21 м? Ответ выразите в км/с.
км/с — скорость света, а v — скорость ракеты (в км/с). Какова должна быть минимальная скорость ракеты, чтобы еe наблюдаемая длина стала не более 21 м? Ответ выразите в км/с.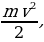 где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях.
где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 10 секунд после начала колебаний. Ответ дайте в джоулях.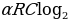
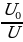 (с), где
(с), где 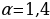 — постоянная. Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло 25,2 с. Ответ дайте в киловольтах.
— постоянная. Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло 25,2 с. Ответ дайте в киловольтах.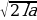 , где
, где 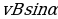 (Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла
(Н) и направленная вверх перпендикулярно плоскости. При каком наименьшем значении угла 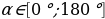 шарик отрывается от поверхности, если для этого нужно, чтобы сила FЛ была не менее чем 6 · 10-8 Н? Ответ дайте в градусах.
шарик отрывается от поверхности, если для этого нужно, чтобы сила FЛ была не менее чем 6 · 10-8 Н? Ответ дайте в градусах.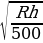 , где R = 6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 5,6 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 10,4 километров?
, где R = 6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 5,6 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 10,4 километров?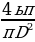 , где m = 2400 кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения g = 10 м/с2, а π = 3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 800 000 Па. Ответ выразите в метрах.
, где m = 2400 кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения g = 10 м/с2, а π = 3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 800 000 Па. Ответ выразите в метрах.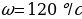 /с, фаза
/с, фаза 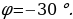 Датчик настроен так, что если напряжение в нем не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
Датчик настроен так, что если напряжение в нем не ниже чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?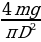 , где m = 1200 кг – общая масса навеса и колонны, D – диаметр колонны (в метрах). Считая ускорение свободного падения g = 10 м/с2, а π = 3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400 000 Па. Ответ выразите в метрах.
, где m = 1200 кг – общая масса навеса и колонны, D – диаметр колонны (в метрах). Считая ускорение свободного падения g = 10 м/с2, а π = 3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400 000 Па. Ответ выразите в метрах.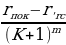 , где m =
, где m = 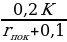 , rпок — средняя оценка магазина покупателями, rэкс — оценка магазина, данная экспертами, K — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 7, их средняя оценка равна 0,32, а оценка экспертов равна 0,22.
, rпок — средняя оценка магазина покупателями, rэкс — оценка магазина, данная экспертами, K — число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 7, их средняя оценка равна 0,32, а оценка экспертов равна 0,22.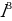 , где
, где 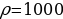 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах.
кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах.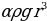 , где
, где 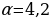 – постоянная,
– постоянная, 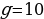 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах.
Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах.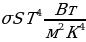 , где Р — мощность излучения звезды (в Ваттах),
, где Р — мощность излучения звезды (в Ваттах),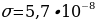 — постоянная, S м
— постоянная, S м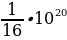 м2, а мощность её излучения равна 9,12 ·1025 Вт. Найдите температуру этой звезды в Кельвинах.
м2, а мощность её излучения равна 9,12 ·1025 Вт. Найдите температуру этой звезды в Кельвинах.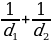 =
= 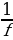 . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чётким. Ответ выразите в сантиметрах.
. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чётким. Ответ выразите в сантиметрах.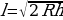 , где R = 6400 (км) — радиус Земли. С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах.
, где R = 6400 (км) — радиус Земли. С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах.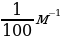 , b =
, b = 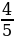 — постоянные параметры, x (м) — смещение камня по горизонтали, y (м) — высота камня над замлей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 14 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
— постоянные параметры, x (м) — смещение камня по горизонтали, y (м) — высота камня над замлей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 14 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?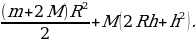 При каком максимальном значении
При каком максимальном значении 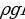 3, где l – длина ребра куба в метрах,
3, где l – длина ребра куба в метрах, 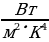 , где Р — мощность излучения звезды (в Ваттах),
, где Р — мощность излучения звезды (в Ваттах),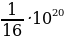 м2, а мощность её излучения равна 9,12 · 1025 Вт. Найдите температуру этой звезды в Кельвинах.
м2, а мощность её излучения равна 9,12 · 1025 Вт. Найдите температуру этой звезды в Кельвинах.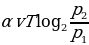 , где
, где 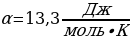 — постоянная, T = 300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15 960 Дж.
— постоянная, T = 300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15 960 Дж.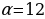 км/ч
км/ч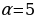 м/с2. За
м/с2. За 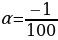 м-1, b = 1 – постоянные параметры, x(m) – смещение камня по горизонтали, y(m) – высота камня над замлей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
м-1, b = 1 – постоянные параметры, x(m) – смещение камня по горизонтали, y(m) – высота камня над замлей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?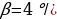 мин2 — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки
мин2 — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки 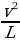 – g), где
– g), где 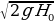 kt +
kt + 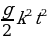 где
где 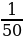 – отношение площадей поперечных сечений крана и бака, а g – ускорение свободного падения (считайте g = 10 м/с
– отношение площадей поперечных сечений крана и бака, а g – ускорение свободного падения (считайте g = 10 м/с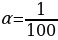 м/мин2, и b = -
м/мин2, и b = - 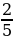 м/мин постоянные,
м/мин постоянные, 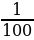 м-1, b = 1 – постоянные параметры, x(м) – смещение камня по горизонтали, y(м) – высота камня над замлей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
м-1, b = 1 – постоянные параметры, x(м) – смещение камня по горизонтали, y(м) – высота камня над замлей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?




















