Задания 15-19 Вариант 5 ОГЭ из 36 вариантов

Задания 15-19 Вариант 5 ОГЭ из 36 вариантов.

Задание 15. Точки М и N являются серединами сторон АВ и ВС треугольника ABC соответственно. Отрезки AN и СМ пересекаются в точке О, AN = 18, CM = 21. Найдите ОМ.

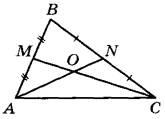
Решение.

Известно, что медианы любого треугольника в точке пересечения делятся в отношении 2:1, считая от вершины. Следовательно, длина отрезка OM, равна:

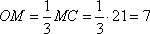
Ответ: 7

Задание 16. Угол А четырёхугольника ABCD, вписанного в окружность, равен 33°. Найдите угол С этого четырёхугольника. Ответ дайте в градусах.

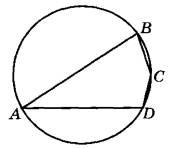
Решение.

Известно, что сумма противоположных углов четырехугольника, вписанного в окружность, равна 180°, то есть:

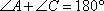
откуда

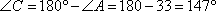
Ответ: 147

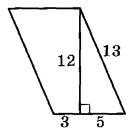
Задание 17. Найдите площадь параллелограмма, изображённого на рисунке.

Решение.

Площадь параллелограмма можно найти как произведение его высоты h=12 на основание a=3+5=8, к которой она проведена:

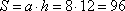
Ответ: 96

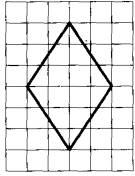
Задание 18. На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите длину его меньшей диагонали.

Решение.

Длина меньшей диагонали ромба показана синей линией на рисунке ниже:

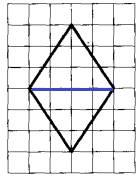
Ее длина составляет 4 клетки.

Ответ: 4

Задание 19. Какое из следующих утверждений не верно?

1) Через заданную точку плоскости можно провести только одну прямую.

2) Все равносторонние треугольники подобны.

3) Сумма острых углов прямоугольного треугольника равна 90 градусам.

Решение.

1) Нет, через точку на плоскости можно провести бессчетное количество прямых.

2) Да, все равносторонние треугольники подобны по трем углам.

3) Да, у прямоугольных треугольников сумма его острых углов всегда 90 градусов.

Ответ: 1