Задания 16-20. Вариант 23. ОГЭ 2020 из 36 вариантов.

Задания 16-20. Вариант 23. ОГЭ 2020 из 36 вариантов.

Задание 16. В остроугольном треугольнике ABC проведена высота ВН, угол ВАС = 63°. Найдите угол АВН. Ответ дайте в градусах.

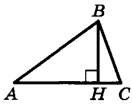
Решение.

Углы BAC и BAH равны, т.к. они образованы одними и теми же лучами. Рассмотрим прямоугольный треугольник ABH, в котором известны два угла: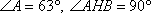 . Учитывая, что сумма углов в треугольнике 180°, получаем значение третьего угла ABH:

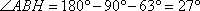
Ответ: 27.

Задание 17. Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.

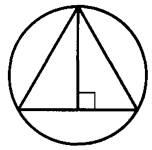
Решение.

Центр описанной около равностороннего треугольника окружности лежит на высоте BH и делит ее в отношении 2:1, считая от вершины B.

В задании нам дана величина радиуса BO=R=12, следовательно, OH=BO:2=6. И вся высота BH=12+6=18.

Ответ: 18.

Задание 18. Диагонали АС и BD трапеции ABCD с основаниями ВС и AD пересекаются в точке О, ВС = 6, AD = 9, АС = 20. Найдите СО.

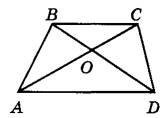
Решение.

Из рисунка видно, что треугольники BCO и AOD подобны друг другу. Следовательно, можно записать отношение

,

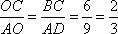то есть точка O делит отрезок AC в отношении 2:3, отсчитывая от вершины C. Это означает, что весь отрезок AC можно разделить на 2+3=5 равных частей, 2 из которых составляет OC, то есть:

.

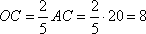Ответ: 8.

Задание 19. На клетчатой бумаге с размером клетки 1x1 изображён параллелограмм. Найдите длину его большей высоты.

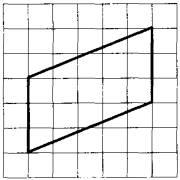
Решение.

Большая высота параллелограмма изображена синей линией на рисунке ниже.

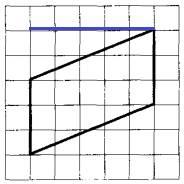
Ее длина составляет 5 клеток.

Ответ: 5.

Задание 20. Какое из следующих утверждений верно?

1) Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.

2) Все диаметры окружности равны между собой.

3) Площадь параллелограмма равна половине произведения его диагоналей.

Решение.

1) Нет, эти треугольники будут подобны (по трем углам), но не равны.

2) Да, все диаметры одной и той же окружности равны.

3) Нет, при вычислении площади нужно еще учесть угол между ними.

Ответ: 12.