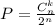Задания № 4 ЕГЭ с решением.

Задание 4. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.

Решение.

В этой задаче имеется фраза «остальные тарелки поступают в продажу», следовательно, не все 100% тарелок поступают в продажу. Вследствие этого, рассуждать будем так. Пусть фабрика выпускает n тарелок. Из них 90% без дефектов, то есть 0,9n, а дефектные составляют долю, равную 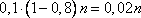. Здесь множитель 0,1 – это 10% дефектных тарелок, а (1-0,8)=0,2 – доля дефектных тарелок (среди 10% дефектных), поступивших в продажу. Таким образом, вероятность покупки не дефектной тарелки, равна:

.

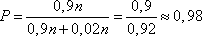Ответ: 0,98.

Задача: 4

На фабрике керамической посуды 20% произведенных тарелок имеют дефект. При контроле качества продукции выявляется 70% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.

Решение:

Из 20% дефектных тарелок отбраковывается 70%, т.е. доля отбракованных тарелок от общего числа составляет 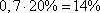. Соответственно в продажу поступает 100%-14% тарелок и среди них не бракованных 86%-6% тарелок. Следовательно, вероятность покупки тарелки без дефектов будет равна

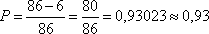
Ответ: 0,93.

Задание 4. На фабрике керамической посуды 30% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 60% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.

Решение.

Из условия задачи следует, что из 30% бракованных тарелок, выявляется только 60%, т.е. 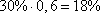 брака от всего объема произведенных тарелок. В продажу поступает  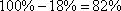тарелок и среди них бракованных 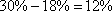. Таким образом, вероятность того, что случайно выбранная тарелка не будет иметь дефектов, равна

.

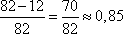Ответ: 0,85.

Задание 4

Монету бросают восемь раз. Во сколько раз событие «орел выпадает ровно 6 раз»
более вероятно, чем событие «орел выпадет ровно один раз»?

Решение

Пусть монету бросают ​n​ раз. Тогда вероятность того, что орел выпадет ровно ​k​ раз можно найти по формуле

​p=Ckn2n​

​Ckn=n!k!(n−k)!​

нам нужно найти ​P1P2​

​P1=8!6!(8−6)!∗28​

​P2=8!1∗7!∗28​

​P1P2=3,5​

Ответ: 3,5

Задание 4

Монету бросают 10 раз. Во сколько раз событие "орел выпадет ровно пять раз" более вероятно, чем "орел выпадет ровно семь раз"?

Решение

(10!)/(5!*5!)- число сочетаний из 10 по 5 число исходов по 5 попаданий

(10!)/(3!*7!)- число сочетаний из 10 по 7 число исходов по 7 попаданий

[(10!)/(5!*5!)]/[(10!)/(3!*7!)]=6*7/(5*4)=2,1

ответ : в 2,1 раза

Задание 4

Монету бросают 9 раз. Во сколько раз событие "орел выпадет ровно семь раз" более вероятно, чем событие "орел выпадет ровно один раз"?

Решение

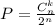
Где

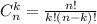
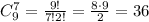
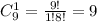
Отношение получается = 36/9 = 4(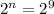сокращаются при делении)

Ответ: в 4 раза

Задание 4

Монету бросают 10 раз. Во сколько раз событие "орел выпадет 8 раз" более вероятно, чем орел выпадет 9 раз?

Решение

Эквивалентно расчету вероятности “решка выпадет 2 раза” больше чем “решка выпадет 1 раз”

10*9/2 и 10*1/1, т.е 45 и 10.

Ответ: в 4.5 раза

Задание 4

Монету бросают 9 раз. Во сколько раз событие орел выпадет ровно 5 раз более вероятно, чем событие орел выпадает ровно 2 раза?

Решение

поскольку при каждом броске возможны только 2 исхода (орел или решка), то при 9 бросках возможны 2⁹ исходов. Из них количество исходов  ровно с 5 выпадениями орла равно 9!/[5!(9-5)!], следовательно вероятность выпадения орла ровно 5 раз равна {9!/[5!(9-5)!]}/2⁹

Повторив аналогичные рассуждения, получим вероятность выпадения орла ровно 2 раза {9!/[2!(9-2)!]}/2⁹

найдем их отношение  [{9!/[5!(9-5)!]}/2⁹]/[{9!/[2!(9-2)!]}/2⁹]=[2!(9-2)!]/[5!(9-5)!]= (1*2*1*2*3*4*5*6*7)/(1*2*3*4*5*1*2*3*4)=(6*7)/(3*4)=3.5

Ответ: В 3,5 раза

Задача 4

Девять детей встают в хоровод в случайном порядке. Среди них Серёжа и его сестра Маша. Какова вероятность того, что Серёжа и Маша окажутся рядом?

Решение

Фиксируем Серёжу (он и так попадет в круг). Остается 8 детей и из них только два благоприятных места в кругу – слева или справа от Маши. Вероятность равна 2/8=0,25.

Ответ:0,25

Задание 4

Одиннадцать детей встают в хоровод в случайном порядке. Среди них Антон и его сестра Маша. Какова вероятность того, что Антон и Маша окажутся рядом?

Решение

Фиксируем Антона (он и так попадет в круг). Остается 10 детей и из них только два благоприятных места в кругу – слева или справа от Маши. Вероятность равна 2/10=0,2.

Ответ:0,2

Задание 4

Девять детей встают в хоровод в случайном порядке. Среди них Дима и его сестра Катя. Какова вероятность того, что Дима и Катя не окажутся рядом.?

Решение

Пусть Дима встал на какое-то место в хороводе. 
У его сестры Кати - шесть мест из оставшихся восьми чтобы не оказаться рядом. 
Р=6/8=0.75

Ответ:0,75

Задание 4

Одиннадцать детей встают в хоровод в случайном порядке. Среди них Максим и его сестра Вика. Какова вероятность того, что Дима и Катя не окажутся рядом.?

Решение

Пусть Максим встал на какое-то место в хороводе. 
У его сестры Вики - 8 мест из оставшихся десяти чтобы не оказаться рядом. 
Р=8/10=0.8

Ответ:0,8

Задача 4

Семнадцать детей встают в хоровод в случайном порядке. Среди них Серёжа и его сестра Таня. Какова вероятность того, что Серёжа и Таня окажутся рядом?

Решение

Фиксируем Серёжу (он и так попадет в круг). Остается 16 детей и из них только два благоприятных места в кругу – слева или справа от Маши. Вероятность равна 2/16=0,125.

Ответ:0,125

Задание 4

Абонент пытается отправить СМС-сообщение, находясь в лесу. Связь плохая, и поэтому сообщение при каждой попытке отправляется

с вероятностью 0,7, независимо от предыдущих попыток. Найдите вероятность того, что три первые попытки отправить сообщение окажутся неудачными.

Решение

Это одна из классических задач теории вероятности. Для её решения необходимо сначала узнать вероятность того, что сообщения не будет отправлено. Это просто. Нужно от 1 вычесть вероятность того что сообщения будет отправлено и получим:  

1 - 0.7 = 0.3;

Теперь мы знаем какая вероятность того что сообщения не будет доставлено с первой попытки. Нам нужно знать вероятность того что оно не будет отправлено за три попытки. Для этого перемножим 0.3 само на себя 3 раза и получим нашу вероятность: 

0.3 * 0.3 * 0.3 = 0.027;

Ответ: 0.027

Задача 4. В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, равна 0,4. Вероятность того, что чай закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.

Решение.

Для решения задачи введем два события

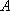 - чай закончится в первом автомате;
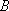 - чай закончится во втором автомате.

События 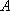 и 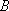 являются совместными, следовательно, вероятность того, что чай закончится хотя бы в одном автомате, будет соответствовать сумме этих вероятностей и равна

.

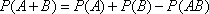Данные вероятности даны по условию задачи и равны

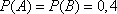 и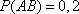 

После подстановки этих значений, получаем

.

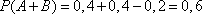Вероятность того, что чай останется в обоих автоматах равна противоположной вероятности 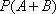, т.е. решением задачи будет

.

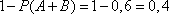Ответ: 0,4

Задача 4

Павел Иванович совершает прогулку из точки A по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадет в точку G.

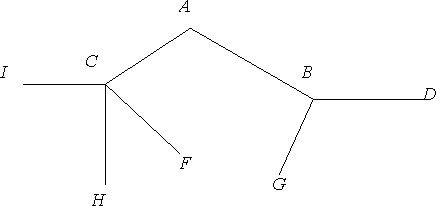
Решение:

Так как дорожки выбираются случайным образом, то вероятность выбора одной дорожки из двух равна 1/2. Чтобы Павлу Ивановичу попасть в точку G необходимо выбрать сначала дорожку, ведущую в точку B (вероятность выбора 1/2), а затем выбрать дорожку, ведущую в точку G (вероятность также 1/2). Таким образом результирующая вероятность того, что он сначала повернет в точку B, а затем в точку G, равна произведению вероятностей этих двух выборов, т.е.

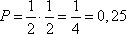
Ответ: 0,25.

Задание 4.

 По отзывам покупателей Игорь Игоревич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,94. Вероятность того, что этот товар доставят из магазина Б, равна 0,8. Игорь Игоревич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.

Решение.

Выделим два события: A – товар не доставлен из первого магазина; B – товар не доставлен из второго магазина. Вероятность события A равна

,

вероятность события B, равна

.

Так как магазины работают независимо друг от друга, то вероятность того, что товар не будет доставлен ни из первого, ни из второго магазина равна

.

Ответ: 0,012.

Задача 4

В сборнике билетов по истории всего 50 билетов, в 13 из них встречается вопрос о Великой Отечественной войне. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос о Великой Отечественной войне.

Решение:

Вероятность того, что школьнику достанется вопрос о Великой Отечественной войне, равна доли этих билетов в общем числе билетов по истории, т.е.

Ответ: .

Задание 4

Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,95. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,04. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.

Решение.

Ситуация, при которой батарейка будет забракована, может сложиться в результате событий: A = батарейка действительно неисправна и забракована справедливо или В = батарейка исправна, но по ошибке забракована. Это несовместные события, вероятность их суммы равна сумме вероятностей эти событий. Имеем:

P(A+B)=P(A)+P(B)=0.03*0.95+0.97*0.04=0.0285+0.0388=0.0673

 

Ответ: 0,0673.

Задание 4. 

Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.

Решение.

Выделим два несовместных исхода, при которых система контроля бракует батарейку:

- батарейка неисправна и она бракуется системой;

- батарейка исправна и она бракуется системой.

Вероятность первого исхода равна , вероятность второго исхода равна . В результате, искомая вероятность, равна:

Ответ: 0,0296.

Задание 4. 

Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,04. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,95. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.

Решение.

Выделим два несовместных исхода, при которых система контроля бракует батарейку:

- батарейка неисправна и она бракуется системой;

- батарейка исправна и она бракуется системой.

Вероятность первого исхода равна P(A)=0.04*0.95, вероятность второго исхода равна P(B)=(1-0.04)*0.01. В результате, искомая вероятность, равна:

P(A+B)=P(A)+P(B)=0.04*0.95+0.96*0.01=0.038+0.0096=0.0476

Ответ: 0,0476.

Задание 4. 

Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,98. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.

Решение.

Выделим два несовместных исхода, при которых система контроля бракует батарейку:

- батарейка неисправна и она бракуется системой;

- батарейка исправна и она бракуется системой.

Вероятность первого исхода равна P(A)=0.02*0.98, вероятность второго исхода равна P(B)=(1-0.02)*0.01. В результате, искомая вероятность, равна:

P(A+B)=P(A)+P(B)=0.02*0.98+0.98*0.01=0.0196+0.0098=0.0294

Ответ: 0,0294.

Задание 4. 

Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,03. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.

Решение.

Выделим два несовместных исхода, при которых система контроля бракует батарейку:

- батарейка неисправна и она бракуется системой;

- батарейка исправна и она бракуется системой.

Вероятность первого исхода равна P(A)=0.05*0.99, вероятность второго исхода равна P(B)=(1-0.05)*0.03. В результате, искомая вероятность, равна:

P(A+B)=P(A)+P(B)=0.05*0.99+0.95*0.03=0.0495+0.0285=0.078

Ответ: 0,059.

Задание 4. 

В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,4. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).

Решение.

Так как клиенты приходят независимо друг от друга, то вероятность занятости продавцов не зависит друг от друга. Следовательно, имеем вероятности занятости каждого из продавцов, не зависимые между собой. И вероятность занятости всех трех продавцов будет равна произведению вероятности занятости каждого из них, т.е. получим

.

Ответ: 0,064.

Задание 4. 

В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).

Решение.

Так как клиенты приходят независимо друг от друга, то вероятность занятости продавцов не зависит друг от друга. Следовательно, имеем вероятности занятости каждого из продавцов, не зависимые между собой. И вероятность занятости всех трех продавцов будет равна произведению вероятности занятости каждого из них, т.е. получим

0.3*0.3*0.3=0.027

Ответ: 0,027.

Задание 4. 

Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,4. На столе лежат 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Решение.

Ковбой Джон может наудачу схватить как пристрелляный, так и не пристрелянный револьвер. Так как на столе 10 револьверов и из них только 4 пристрелянные, то вероятность выбора пристрелянного револьвера равна

,

а непристрелянного

.

Известно, что если он выстреливает из пристрелянного револьвера, то попадает в цель с вероятностью 0,9, значит, вероятность такого события будет равна

,

а вероятность выбора непристрелянного револьвера и попадания из него в цель, равна

.

Если произойдет или первое или второе событие, то Ковбой Джон попадет в цель и вероятность этого события равна

,

тогда вероятность промаха

.

Ответ: 0,4.

Задача 4. 

В некотором городе из 2000 появившихся на свет младенцев 990 девочек. Найдите частоту рождения мальчиков в этом городе. Результат округлите до тысячных.

Решение.

Частота рождения мальчиков будет равна доли рождения мальчиков в этом городе. Всего рождается 2000 детей, девочек 990, значит мальчиков рождается

2000-990=1010

Частота их рождения

.

Ответ: .

Задание 4. 

В случайном эксперименте бросают две игральные кости (кубика). Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.

Решение.

Пусть событие А обозначает выпадение в сумме 7 очков при бросании двух игральных кубиков. Тогда число благоприятных исходов для события А будет равно: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1, т.е. 6 событий. Всего исходов . Таким образом, вероятность события А равна

.

Ответ: 0,17.

Задание 4.

 Марина и Дина бросают кубик по одному разу. Выигрывает та девочка, у которой выпадет больше очков. Первой кубик бросила Марина, у нее выпало 3 очка. Найдите вероятность того, что Дина выиграет.

Решение.

Кубик бросается один раз. Марина уже бросила кубик и у нее выпало 3 очка. Дина может выиграть у Марины, если при бросании игрального кубика выпадут числа 4, 5 или 6. Всего возможных исходов 6. Следовательно, вероятность того, что Дина выиграет, равна

.

Ответ: 0,5.

Задание 4.

 В группе туристов 8 человек. С помощью жребия они выбирают шестерых человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?

Решение.

Турист Д. – один из 8 человек, которые участвуют в жребии, значит, общее число исходов n=8. С помощью жребия выбирается 6 человек, значит, число благоприятных исходов для туриста Д., равно m=6. Получаем искомую вероятность:

Ответ: 0,75.

Задание 4

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что разница выпавших очков равна 1 или 2.

Решение

Выпишем все комбинации удовлетворяющие условию 

1,2 и 2,1
1,3 и 3,1
2,3 и 3,2
2,4 и 4,2
3,4 и 4,3
3,5 и 5,3
4,5 и 5,4
4,6 и 6,4
5,6 и 6,5

Всего их M = 18

Всевозможные комбинацию: N = 6·6

По классической формуле определения вероятности, имеем:

P = M/N = 18/36 = 0.5

Задание 4.

 В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что сумма выпавших очков равна 5. Результат округлите до тысячных.

Решение.

Каждая грань игральной кости пронумерована от 1 до 6. Следовательно, при бросании трех игральных костей, сумма в 5 очков может получиться при следующих комбинациях:

1+1+3

1+2+2

1+3+1

2+1+2

2+2+1

3+1+1

то есть имеем 6 благоприятных исходов. Всего возможных комбинаций равно . Таким образом, искомая вероятность, равна:

.

Ответ: 0,028.

Задание 4

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что одновременно хотя бы на одном кубике выпало число 1 и ни на одном кубике не выпало число 6.

Решение

Вероятность выпадения какого-либо заранее определенного значения кости с шестью гранями равна 1/6.
Бросаем первый кубик. Вероятность выпаднния 1 равна 1/6
Бросаем второй, вероятность того, что не выпадет 6 равна 1-1/6=5/6
Вероятность того, что эти события произойдут при одном броске равна (1/6)*(5/6)=5/36
Но все может произойти наоборот: единица выпадет на второй кости, а не 6 на первой. Такая вероятность тоже 5/36
поэтому общая вероятность равна 5/36 + 5/36=5/18

Задание 4

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что произведение выпавших очков делится на 5, но не делится на 30.

Решение

1, 5
2, 5
3, 5
4, 5
5, 5
6, 5 – не подходит, так как делится на 30
то есть 5 вариантов
5, 1
...
5, 4
еще 4 варианта (5, 6 и 5, 5 исключили по понятным причинам)
всего вариантов 6·6 = 36
P = (4+5)/36 = 9/36 = 0.25

Задание 4.

 В случайном эксперименте бросают две игральные кости (кубика). Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.

Решение.

Пусть событие А обозначает выпадение в сумме 7 очков при бросании двух игральных кубиков. Тогда число благоприятных исходов для события А будет равно: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1, т.е. 6 событий. Всего исходов . Таким образом, вероятность события А равна

.

Ответ: 0,17.

Задание 4. 

Стрелок в тире стреляет по мишени до тех пор, пока не попадёт в неё. Вероятность попадания при каждом отдельном выстреле равна р = 0,6. Найдите вероятность того, что стрелку потребуется ровно три попытки.

Решение.

Стрелку потребуется 3 попытки, если при первых двух он промахнется (вероятность этого события равна 1-0,6=0,4), а третий раз попадет. Все эти независимые события должны произойти друг за другом. Получаем произведение их вероятностей:

Ответ: 0,096.

Задание 4. 

Двое играют в кости — они по разу бросают игральный кубик. Выигрывает тот, у кого больше очков. Если выпадает поровну, то наступает ничья. Первый бросил кубик, и у него выпало 4 очка. Найдите вероятность того, что он выиграет.

Решение.

Чтобы первый игрок выиграл, у второго игрока должно выпасть или 1, или 2, или 3 – всего 3 варианта (благоприятных исходов для выигрыша). Всего исходов 6, следовательно, искомая вероятность равна

.

Ответ: 0,5.

Задание 4

В группе туристов 10 человек, в том числе турист А. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Какова вероятность того, что туристу А. выпадет по жребию идти в село?

Решение:

При однократом бросании жребия вероятность того, что туристу А. выпадет пойти в село равна 1/10. Так как жребий бросается дважды, то искомая вероятность удваивается, т.е ответ 2/10=1/5=0,2.

Ответ: 0,2.

Задание 4

Перед началом матча по футболу судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда «Белые» по очереди играет с командами «Красные», «Синие» и «Зеленые». Найдите вероятность того, что ровно в двух матчах из трех право владеть мячом получит команда «Белые».

Решение:

Для решения данной задачи выделим событие A – команда «Белые» имеет право владеть мячом. Нам важно найти вероятность возникновения события A ровно 2 раза в 3 экспериментах. Это можно вычислить по формуле Бернулли

где  - число сочетаний из n по m (т.е. сколько комбинаций в m появлений события A может быть в серии из n экспериментов);  - вероятность появления события A в одном эксперименте.

В нашем случае , , а вероятность появления события A в одном эксперименте, равна

,

так как при встрече играет по 2 команды и каждая случайным образом может владеть мячом. В итоге получаем решение задачи

Ответ: .

Задание 4. 

В каждой пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Галя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Галя не найдёт приз в своей банке.

Решение.

Приз находится, в среднем, в одной банке из 5 (значит 4 банки без приза), следовательно, вероятность покупки банки без приза, равна 4/5=0,8.

Ответ: 0,8.

Задание 4. 

В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно три раза.

Решение.

Обозначим через событие A выпадение орла ровно три раза при четырех бросаниях монеты. Общее число благоприятных исходов  для события A можно найти по формуле

,

где  - число выпадений орла;  - общее число подбрасываний монетки, имеем:

.

Всего возможных исходов равно . Таким образом, вероятность события A это

.

Ответ: 0,25.

Задание 4

При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,3, а при каждом последующем – 0,9. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,96?

Решение:

Для решения данной задачи проще вычислить вероятность обратного события, т.е. найти вероятность не попадания в цель ни при одном выстреле, ни при двух выстрелах, ни при трех выстрелах и т.д. Вероятность не поражения цели при одном выстреле будет равна

при двух

при трех

и т.д.

Зная вероятность не попадания в цель при заданном числе выстрелов , можно легко вычислить вероятность поражения цели как , где  - число выстрелов.

Найдем теперь число выстрелов, при котором вероятность попадания не менее 0,96, получим:

- при одном выстреле

- при двух выстрелах

- при трех выстрелах

Ответ: 3 выстрела.

Задание 4. 

Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 6, но не дойдя до отметки 9.

Решение.

Весь циферблат соответствует единичной вероятности того, что стрелки остановятся на какой-либо отметки. Сектор от 6 до 9 образует четверть этого циферблата, следовательно, вероятность попадания в него часовой стрелки равна

.

Ответ: 0,25.

Задание 4.

 В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Решение.

Общее число равновозможных комбинаций может быть четыре:

«орел-орел», «орел-решка», «решка-орел», «решка-решка».

Из них благоприятных исходов по условию задачи два – это «орел-решка» и «решка-орел». Следовательно, искомая вероятность, равна

.

Ответ: 0,5.