Подборка заданий для подготовки к ОГЭ по математике для учащихся 9 «Б» класса.
Май 2017
1. Действия с обыкновенными дробями
1. Найдите значение выражения  2.
2.  3.
3.  4.
4. 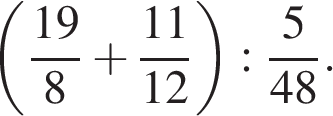
5.  6.
6.  7.
7.  8.
8.  9.
9. 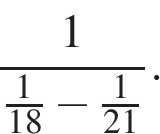
2. Арифметическая прогрессия
1. Дана арифметическая прогрессия:  Найдите сумму первых десяти её членов.
Найдите сумму первых десяти её членов.
2. Дана арифметическая прогрессия  Найдите
Найдите  .
.
3. Дана арифметическая прогрессия  Найдите сумму первых десяти её членов.
Найдите сумму первых десяти её членов.
4. Выписаны первые несколько членов арифметической прогрессии: 3; 6; 9; 12;… Какое из следующих чисел есть среди членов этой прогрессии? 1) 83 2) 95 3) 100 4) 102
5. Арифметические прогрессии 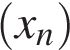 ,
,  и
и  заданы формулами n-го члена:
заданы формулами n-го члена:  ,
,  ,
,  Укажите те из них, у которых разность
Укажите те из них, у которых разность  равна 4.
равна 4.
1) 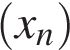 и
и  2)
2)  и
и  3)
3) 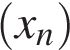 ,
,  и
и  4)
4) 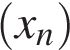
6. В первом ряду кинозала 30 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в ряду с номером n?
1) 2) 3) 4) 
7. Дана арифметическая прогрессия: 33; 25; 17; … Найдите первый отрицательный член этой прогрессии. 1)  2)
2)  3)
3)  4)
4) 
8. Арифметическая прогрессия задана условиями: , . Какое из данных чисел является членом этой прогрессии?
, . Какое из данных чисел является членом этой прогрессии?
1) 80 2) 56 3) 48 4) 32
9. Найдите сумму всех отрицательных членов арифметической прогрессии: −8,6; −8,4; ...
10. Арифметическая прогрессия  задана формулой n-го члена и известно, что
задана формулой n-го члена и известно, что  . Найдите пятый член этой прогрессии.
. Найдите пятый член этой прогрессии.
11. В арифметической прогрессии  известно, что . Найдите четвёртый член этой прогрессии.
известно, что . Найдите четвёртый член этой прогрессии.
12. Арифметическая прогрессия задана условиями: . Найдите сумму первых 19 её членов.
13. Какое наибольшее число последовательных натуральных чисел, начиная с 1, можно сложить, чтобы получившаяся сумма была меньше 528?
14. Найдите сумму всех положительных членов арифметической прогрессии 11,2; 10,8; …
15. Какое наименьшее число последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы получившаяся сумма была больше 465?
16. Найдите сумму всех отрицательных членов арифметической прогрессии –7,2; –6,9; …
17. Арифметическая прогрессия (an) задана условиями: a1 = 3, an + 1 = an + 4. Найдите a10.
18. Записаны первые три члена арифметической прогрессии: 20; 17; 14. Какое число стоит в этой арифметической прогрессии на 91-м месте?
19. Дана арифметическая прогрессия (аn): −6; −2; 2; … . Найдите a16.
20. Выписаны первые несколько членов арифметической прогрессии: −87 ; −76; −65; … Найдите первый положительный член этой прогрессии.
21. В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду?
22. Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 8 квадратов больше, чем в предыдущей. Сколько квадратов в 16-й строке?
23. Выписано несколько последовательных членов арифметической прогрессии: …; −9; x; −13; −15; … Найдите член прогрессии, обозначенный буквой x .
24. Дана арифметическая прогрессия (an), разность которой равна 2,5, a1 = 8,7. Найдите a9.
25. Даны пятнадцать чисел, первое из которых равно 6, а каждое следующее больше предыдущего на 4. Найти пятнадцатое из данных чисел.
26. Дана арифметическая прогрессия (an), разность которой равна −8,5, a1 = −6,8. Найдите a11.
27. Арифметическая прогрессия  задана условиями: Найдите
задана условиями: Найдите 
28. Дана арифметическая прогрессия (an), для которой a10 = 19, a15 = 44. Найдите разность прогрессии.
29. Арифметическая прогрессия задана условием an = −0,6 + 8,6n. Найдите сумму первых 10 её членов.
30. Дана арифметическая прогрессия (an), разность которой равна −2,5, a1 = −9,1. Найдите сумму первых 15 её членов.
31. Арифметическая прогрессия задана условием an = −11,9 + 7,8n . Найдите a11.
32. Первый член арифметической прогрессии равен −11,9, а разность прогрессии равна 7,8. Найдите двенадцатый член этой прогрессии.
33. Дан числовой набор. Его первое число равно 6,2, а каждое следующее число на 0,6 больше предыдущего. Найдите пятое число этого набора.
34. Выписаны первые несколько членов арифметической прогрессии: −26 ; −20; −14; … Найдите первый положительный член этой прогрессии.
35. Дана арифметическая прогрессия (an), разность которой равна 1,1, a1 = −7. Найдите сумму первых 8 её членов.
36. Арифметическая прогрессия задана условием an = 1,9 - 0,3n. Найдите сумму первых 15 её членов.
3. Геометрическая прогрессия
1. В геометрической прогрессии  известно, что . Найти пятый член этой прогрессии. - 64
известно, что . Найти пятый член этой прогрессии. - 64
2. Геометрическая прогрессия  задана формулой
задана формулой  - го члена . Укажите четвертый член этой прогрессии. -54
- го члена . Укажите четвертый член этой прогрессии. -54
3. Дана геометрическая прогрессия (bn), знаменатель которой равен 2, а . Найдите сумму первых шести её членов.
4. В геометрической прогрессии сумма первого и второго членов равна 75, а сумма второго и третьего членов равна 150. Найдите первые три члена этой прогрессии. В ответе перечислите через точку с запятой первый, второй и третий члены прогрессии.
5. Геометрическая прогрессия задана условием Найдите сумму первых её 4 членов.
6. Выписаны первые несколько членов геометрической прогрессии: 17, 68, 272, ... Найдите её четвёртый член.
7. Выписано несколько последовательных членов геометрической прогрессии: … ; 150 ; x ; 6 ; 1,2 ; … Найдите член прогрессии, обозначенный буквой x.
8. Выписаны первые несколько членов геометрической прогрессии: −1024; −256; −64; … Найдите сумму первых 5 её членов.
9. Геометрическая прогрессия задана условием Найдите сумму первых её 4 членов.
10. Выписано несколько последовательных членов геометрической прогрессии: … ; 1,75; x; 28 ; −112; … Найдите член прогрессии, обозначенный буквой x.
11. Дана геометрическая прогрессия (bn), для которой b5 = −14, b8 = 112. Найдите знаменатель прогрессии.
12. Геометрическая прогрессия задана условием b1 = −7, bn + 1 = 3bn. Найдите сумму первых 5 её членов.
13. Дана геометрическая прогрессия (bn), знаменатель которой равен 2, а b1 = 16. Найдите b4.
14. Дана геометрическая прогрессия (bn), знаменатель которой равен 5, а Найдите сумму первых 6 её членов.
15. Выписаны первые несколько членов геометрической прогрессии: − 256; 128; − 64; … Найдите сумму первых семи её членов.
16. Дана геометрическая прогрессия (bn), для которой b3 =  , b6 = -196. Найдите знаменатель прогрессии.
, b6 = -196. Найдите знаменатель прогрессии.
17. Геометрическая прогрессия задана условием b1 = −3, bn + 1 = 6bn. Найдите сумму первых 4 её членов.
18. Выписано несколько последовательных членов геометрической прогрессии: … ; -12 ; x ; -3 ; 1,5 ; … Найдите член прогрессии, обозначенный буквой x. Х=6
4. Разные задачи
2. На многопредметной олимпиаде  всех участников получили дипломы,
всех участников получили дипломы, остальных участников были награждены похвальными грамотами, а остальные 144 человека получили сертификаты об участии. Сколько человек участвовало в олимпиаде? х=231
остальных участников были награждены похвальными грамотами, а остальные 144 человека получили сертификаты об участии. Сколько человек участвовало в олимпиаде? х=231
3. На складе есть коробки с ручками двух цветов: чёрные и синие. Коробок с чёрными ручками 4, с синими — 11. Сколько всего ручек на складе, если чёрных ручек 640, коробки одинаковые и в каждой коробке находятся ручки только одного цвета? 640 + 11*160= 2400
4. На молочном заводе пакеты молока упаковываются по 12 штук в коробку, причём в каждой коробке все пакеты одинаковые. В партии молока, отправляемой в магазин «Уголок», коробок с полуторалитровыми пакетами молока втрое меньше, чем коробок с литровыми пакетами. Сколько литров молока в этой партии, если коробок с литровыми пакетами молока 45?(45*1+15*1,5)*12=810
5. За 20 минут велосипедист проехал 7 километров. Сколько километров он проедет за 35 минут, если будет ехать с той же скоростью? 12,25 км
6. Принтер печатает одну страницу за 12 секунд. Сколько страниц можно напечатать на этом принтере за 8 минут? 60*8=480 сек. 480:12= 40 стр
7. Расстояние от Солнца до Юпитера равно 779 000 000 км. Сколько времени идёт свет от Солнца до Юпитера? Скорость света равна 300 000 км/с. 43,3 мин Ответ дайте в минутах и округлите до десятых.
8. Масштаб карты 1:100 000. Чему равно расстояние между городами A и B (в км), если на карте оно составляет 2 см? 20 км
9. Расстояние от Солнца до Нептуна свет проходит примерно за 252,95 минуты. Найдите приблизительно расстояние от Солнца до Нептуна, ответ округлите до миллионов км. Скорость света равна 300 000 км/с. 4553,1 млн. км
10. Из объявления фирмы, проводящей обучающие семинары:
«Стоимость участия в семинаре — 3000 р. с человека. Группам от организаций предоставляются скидки: от 3 до 10 человек — 5%; более 10 человек — 8%». Сколько рублей должна заплатить организация, направившая на семинар группу из 4 человек? 11400 руб
11. Поезд, двигаясь равномерно со скоростью 150 км/ч, проезжает мимо столба за 6 секунд. Найдите длину поезда в метрах. 250 м
12. В начале года число абонентов телефонной компании «Восток» составляло 800 тыс. человек, а в конце года их стало 880 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании? На 10%
13. Поезд, двигаясь равномерно со скоростью 150 км/ч, проезжает мимо столба за 18 секунд. Найдите длину поезда в метрах. 750 м
5. Проценты
1. Стоимость проезда в пригородном электропоезде составляет 198 рублей. Школьникам предоставляется скидка 50%. Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников?
2. Чашка, которая стоила 90 рублей, продаётся с 10%-й скидкой. При покупке 10 таких чашек покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен получить?
3. Городской бюджет составляет 45 млн. р., а расходы на одну из его статей составили 12,5%. Сколько рублей потрачено на эту статью бюджета?
4. Сберегательный банк начисляет на срочный вклад 20% годовых. Вкладчик положил на счет 800 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет?
5. Товар на распродаже уценили на 20%, при этом он стал стоить 680 р. Сколько стоил товар до распродажи?
6. Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 40 млн. р. Какая сумма в рублях из этой прибыли должна пойти на выплату частным акционерам?
7. Акции предприятия распределены между государством и частными лицами в отношении 3:5. Общая прибыль предприятия после уплаты налогов за год составила 32 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?
Ответ укажите в рублях.
8. Средний вес мальчиков того же возраста, что и Сергей, равен 48 кг. Вес Сергея составляет 120% среднего веса. Сколько весит Сергей?
9. В начале года число абонентов телефонной компании «Север» составляло 200 тыс. чел., а в конце года их стало 210 тыс. чел. На сколько процентов увеличилось за год число абонентов этой компании?
10. Тест по математике содержит 30 заданий, из которых 18 заданий по алгебре, остальные –– по геометрии. В каком отношении содержатся в тесте алгебраические и геометрические задания?
1) 3:2 2) 2:3 3) 3:5 4) 5:3
11. На счет в банке, доход по которому составляет 15% годовых, внесли 24 тыс. р. Сколько тысяч рублей будет на этом счете через год, если никаких операций со счетом проводиться не будет? 27600 руб
12. Какая сумма (в рублях) будет проставлена в кассовом чеке, если стоимость товара 520 р., и покупатель оплачивает его по дисконтной карте с 5%-ной скидкой? 494 руб
13. В понедельник некоторый товар поступил в продажу по цене 1000 р. В соответствии с принятыми в магазине правилами цена товара в течение недели остается неизменной, а в первый день каждой следующей недели снижается на 20% от предыдущей цены. Сколько рублей будет стоить товар на двенадцатый день после поступления в продажу?
14. Брюки дороже рубашки на 20%, а пиджак дороже рубашки на 44%. На сколько процентов пиджак дороже брюк? Брюки – 1,2х, пиджак – 1,44х Ответ: на 24%
15. Виноград стоит 160 рублей за килограмм, а малина — 200 рублей за килограмм. На сколько процентов виноград дешевле малины? На 25%
16. Кисть, которая стоила 240 рублей, продаётся с 25%-й скидкой. При покупке двух таких кистей покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить? 140 руб
17. Спортивный магазин проводит акцию: «Любая футболка по цене 300 рублей. При покупке двух футболок — скидка на вторую 60%». Сколько рублей придётся заплатить за покупку двух футболок?
18. В течение августа помидоры подешевели на 50%, а затем в течение сентября подорожали на 70%. Какая цена меньше: в начале августа или в конце сентября — и на сколько процентов?
В ответе укажите количество процентов.
19. Поступивший в продажу в апреле мобильный телефон стоил 4000 рублей. В сентябре он стал стоить 2560 рублей. На сколько процентов снизилась цена на мобильный телефон в период с апреля по сентябрь?
20. Туристическая фирма организует трехдневные автобусные экскурсии. Стоимость экскурсии для одного человека составляет 3500 р. Группам предоставляются скидки: группе от 3 до 10 человек — 5%, группе более 10 человек — 10%. Сколько заплатит за экскурсию группа из 8 человек?
21. Расходы на одну из статей городского бюджета составляют 12,5%. Выразите эту часть бюджета десятичной дробью.
22. Содержание некоторого вещества в таблетке витамина составляет 2,5%. Выразите эту часть десятичной дробью.
23. Плата за телефон составляет 340 рублей в месяц. В следующем году она увеличится на 2%. Сколько придётся платить ежемесячно за телефон в следующем году?
24. В период распродажи магазин снижал цены дважды: в первый раз на 30%, во второй — на 45%. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 1400 р.?
25. На предприятии работало 240 сотрудников. После модернизации производства их число сократилось до 192. На сколько процентов сократилось число сотрудников предприятия?
26.
В начале 2010 г. в поселке было 730 жителей, а в начале 2011 г. их стало 803. На сколько процентов увеличилось число жителей поселка за год?
27. После уценки телевизора его новая цена составила 0,52 старой. На сколько процентов уменьшилась цена телевизора в результате уценки?
28. Число дорожно-транспортных происшествий в летний период составило 0,71 их числа в зимний период. На сколько процентов уменьшилось число дорожно-транспортных происшествий летом по сравнению с зимой?
29.
В начале учебного года в школе было 1250 учащихся, а к концу года их стало 950. На сколько процентов уменьшилось за год число учащихся?
30. Клубника стоит 180 рублей за килограмм, а виноград – 160 рублей за килограмм. На сколько процентов клубника дороже винограда?
31. Магазин делает пенсионерам скидку на определённое количество процентов от стоимости покупки. Десяток яиц стоит в магазине 35 рублей, а пенсионер заплатил за них 33 рубля 25 копеек. Сколько процентов составляет скидка для пенсионера?
32. Магазин детских товаров закупает погремушку по оптовой цене 260 рублей за одну штуку и продаёт с 40-процентной наценкой. Сколько будут стоить 3 такие погремушки, купленные в этом магазине?
33. Суточная норма потребления витамина С для взрослого человека составляет 60 мг. Один помидор в среднем содержит 17 мг витамина С. Сколько процентов суточной нормы витамина С получил человек, съевший один помидор? Ответ округлите до целых.
34. В городе 190 000 жителей, причем 29% – это пенсионеры. Сколько примерно человек составляет эта категория жителей? Ответ округлите до тысяч.
6. Статистика, теоремы о вероятностных событиях
1. Записан рост (в сантиметрах) пяти учащихся: 158, 166, 134, 130, 132. На сколько отличается среднее арифметическое этого набора чисел от его медианы? На 10
2. Фирма «Вспышка» изготавливает фонарики. Вероятность того, что случайно выбранный фонарик из партии бракованный, равна 0,02. Какова вероятность того, что два случайно выбранных из одной партии фонарика окажутся небракованными?
3. Средний рост жителя города, в котором живет Даша, равен 170 см. Рост Даши 173 см. Какое из следующих утверждений верно?
1) Даша — самая высокая девушка в городе.
2) Обязательно найдется девушка ниже 170 см.
3) Обязательно найдется человек ростом менее 171 см.
4) Обязательно найдется человек ростом 167 см.
4. Известно, что в некотором регионе вероятность того, что родившийся младенец окажется мальчиком, равна 0,512. В 2010 г. в этом регионе на 1000 родившихся младенцев в среднем пришлось 477 девочек. Насколько частота рождения девочек в 2010 г. в этом регионе отличается от вероятности этого события?
5. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
6. На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Углы», равна 0,1. Вероятность того, что это окажется задача по теме «Параллелограмм», равна 0,6. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
7. Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 4 или 7.
7. Вычисление по формуле
1. В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле , где  — длительность поездки, выраженная в минутах . Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.
— длительность поездки, выраженная в минутах . Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.
2. Площадь параллелограмма можно вычислить по формуле , где  — стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и .
— стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и .
3. В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле , где  — число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 11 колец.
— число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 11 колец.
4. Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошёл человек, если l = 80 см, n = 1600? Ответ выразите в километрах.
5. Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.
6. Из формулы центростремительного ускорения a = ω2R найдите R (в метрах), если ω = 4 с−1 и a = 64 м/с2.
Часть 2
Алгебраические выражения
1. Сократите дробь . 2. Разложите на множители: .
3. Сократите дробь 4. Упростите выражение
5. Один из корней уравнения равен 1. Найдите второй корень.
6. Упростите выражение: . 7. Упростите выражение: .
8. Упростите выражение: .
9. Упростите выражение: 14. Упростите выражение
10. Найдите значение выражения: при 
11. Сократите дробь: 17. Сократите дробь
12. Какое из чисел больше: или ?
13. Сократите дробь , если .
15. Сократите дробь 16. Сократите дробь
18. Найдите значение выражения при 

19. Найдите значение выражения если
20. Найдите значение выражения если
21. Найдите значение выражения если
22. Найдите значение выражения при 
23. Сократите дробь 24. Сократите дробь
25. Найдите значение выражения если
Задачи на проценты, сплавы и смеси
1. Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?
Решение. Пусть х кг и у кг — массы первого и второго растворов, взятые при смешивании. Тогда х+у +5 кг — масса полученного раствора, содержащего 0,6х + 0,3у кг кислоты. Концентрация кислоты в полученном растворе 20 %, откуда 0,6х + 0,3у = 0,2 (х+у+5)
0,6х +0,3у +5*0,9 = 0,7 (х+у+5)
Решим систему двух полученных уравнений:
Ответ: 2 кг.
2. Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?
Пусть первый сплав взят в количестве x кг, тогда он будет содержать 0,6x кг меди, а второй сплав взят в количестве y кг, тогда он будет содержать 0,45y кг меди. Соединив два этих сплава, получим сплав меди массой x + y, по условию задачи он должен содержать 0,55(x + y) меди. Следовательно, можно составить уравнение: 0,6х + 0,45 у = 0,55(х+у)
Выразим x через y: х = 2у. Следовательно, отношение, в котором нужно взять сплавы: 2 : 1
3. При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?
Пусть первый раствор взят в количестве х грамм, тогда он содержит 0,2х грамм чистой кислоты, а второй раствор взят в количестве у грамм, тогда он содержит 0,5у грамм чистой кислоты. При смешивании двух этих растворов получится раствор массой 0,2х + 0,5у грамм, по условию задачи, он содержит 0,3(х + у) чистой кислоты. Следовательно, можно составить уравнение: 0,2х + 0,5у = 0,3(х + у)
Выразим x через y: 0,1х = 0,2у. х = 2у Следовательно, отношение, в котором нужно взять сплавы: 2 : 1
4. На пост главы администрации города претендовало три кандидата: Журавлёв, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлёва, а за Зайцева — в 3 раза больше, чем за Журавлёва и Иванова вместе. Сколько процентов голосов было отдано за победителя?
5. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.
6. Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?
7. Смешали некоторое количество 10-процентного раствора некоторого вещества с таким же количеством 12-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
8. Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
9. Имеются два сосуда, содержащие 4 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 57% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится в первом растворе?
10. Имеются два сосуда, содержащие 40 кг и 30 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 73% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 72% кислоты. Сколько килограммов кислоты содержится во втором растворе?
11. Имеются два сосуда, содержащие 40 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 33% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 47% кислоты. Сколько килограммов кислоты содержится в первом растворе?
12. Имеются два сосуда, содержащие 24 кг и 26 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 39% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится в первом растворе?
13. Имеются два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 83% кислоты. Сколько килограммов кислоты содержится во втором растворе?
14. Имеются два сосуда, содержащие 22 кг и 18 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 32% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 30% кислоты. Сколько килограммов кислоты содержится в первом растворе?
15. Имеются два сосуда, содержащие 30 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 40% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 37% кислоты. Сколько килограммов кислоты содержится во втором растворе?
16. Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится во втором растворе?
17. Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
18. Свежие фрукты содержат 93% воды, а высушенные — 16%. Сколько сухих фруктов получится из 252 кг свежих фруктов?