Задания олимпиады по математике для студентов 1 курса СПО
2017 – 2018 учебный год
Докажите, что  при любом натуральном п делится на 3.
при любом натуральном п делится на 3.
В трапеции ABCD длина основания AD равна  , а длина основания BC равна
, а длина основания BC равна . Угол A = 15°, D = 30°. Найдите длину боковой стороны AB.
. Угол A = 15°, D = 30°. Найдите длину боковой стороны AB.
Какое наибольшее число натуральных слагаемых можно разложить число 96 так, чтобы все слагаемые были больше 1 и попарно взаимно просты?
Три подруги были в белом, красном и голубом платьях. Их туфли были так же трех цветов. Только у Тамары цвета платья и туфель совпадали. Валя была в белых туфлях. Ни платье, ни туфли Лиды не были красными. Определите цвет платья и туфель каждой из подруг.
Решить в целых числах систему уравнений
 ху + z = 94,
ху + z = 94,
х + уz = 95.
По дороге едут велосипедисты: на запад – Вася и Петя с равными между собой скоростями, а на восток – Коля и Миша с равными между собой скоростями. Вася встретился с Мишей в 12.00, Петя с Мишей – в 15.00, Вася с Колей – в 14.00. Когда встретились, Петя с Колей?
В мешке лежат 26 синих и красных шаров. Среди любых 18 шаров есть хотя бы один синий, а среди любых 10 шаров есть хотя бы один красный. Сколько красных шаров в мешке?
Морская вода содержит 5 процентов соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составила 1,5 процентов.
Решите уравнение 
В правильной треугольной пирамиде SABC с вершиной S SA/AB = 2. Проведены высота AD треугольника SAB и медиана BM треугольника ABC. Найдите отношение MD/BD.
Решения
Решение.
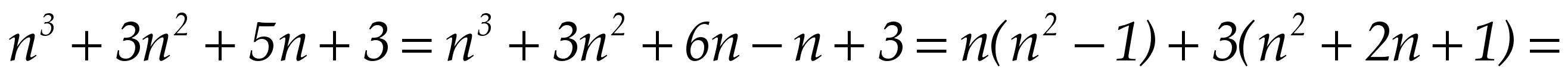
 , т.к. первое слагаемое – это произведение трех последовательных натуральных чисел, т.е. оно кратно 3, а второе слагаемое содержит множитель 3, значит и вся сумма кратна 3.
, т.к. первое слагаемое – это произведение трех последовательных натуральных чисел, т.е. оно кратно 3, а второе слагаемое содержит множитель 3, значит и вся сумма кратна 3.
Решение.
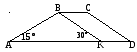
Проведем BK параллельно CD. Заметим KD || BC, KB || DC, следовательно, KBCD параллелограмм и KD = BC = . AD – секущая параллельных прямых BK и CD, следовательно AKB =ADC = 30°.
. AD – секущая параллельных прямых BK и CD, следовательно AKB =ADC = 30°.
Далее найдем длину отрезка AK = AD – KD =  . Боковую сторону AB теперь можно найти по теореме синусов для треугольника ABK:
. Боковую сторону AB теперь можно найти по теореме синусов для треугольника ABK:  . При этом ABK = 180° – AKB – BKA = 180° – 30°– 15° = 135°.
. При этом ABK = 180° – AKB – BKA = 180° – 30°– 15° = 135°.
И sin 135° =  . Теперь можно найти AB, она получается равной 1.
. Теперь можно найти AB, она получается равной 1.
Ответ: 1.
Ответ: на семь слагаемых.
Решение. Приведём пример разбиения числа 96 на семь слагаемых:
9 6 = 2 + 5 + 7 + 11 + 13 + 17 + 41.
Если слагаемых больше, то среди них не менее восьми нечётных (если их семь, то сумма нечётна). Заменим каждое из них на наименьший простой сомножитель. При этом сумма не увеличится, и все слагаемые будут различны. Но сумма восьми наименьших нечётных простых чисел равна 98.
Решение.
| Имя | Белое платье | Красное платье | Голубое платье | Туфли |
| Тамара | - | + | - | Красные |
| Лида | + | - |
| Голубые |
| Валя |
|
| + | Белые |
Ответ: у Тамары были красные туфли и платье, у Вали – белые туфли и голубое платье, у Лиды – белое платье и голубые туфли.
Ответ: х = 95, у = 0, z = 94 или х = 31, у = 2, z = 32.
Решение. Вычтя из второго уравнения первое, получим (х - z)(1 - у) = 1.
По условию, х, у, z целые, тогда возможны два случая:
1) х– z = 1, 1 – у = 1, т. е. у = 0. Подставив значение у в систему, получим: z =94, x=95.
2) х –z = -1, 1 – у = - 1, т. е. z = х +1, у = 2. Подставим найденные значения у и z в первое уравнение, получим 2х + х +1 = 94, х = 31. Отсюда z = 32 .
Ответ. в 17.00.
Решение. Расстояние между Мишей и Колей и их скорости не меняются, а скорости Васи и Пети равны. Вася встретил Колю через 2 часа после Миши, значит, Петя встретят Колю тоже через 2 часа после Миши, т. е. в 17.00.
Ответ. 17.
Решение. Так как из 18 шаров найдется хотя бы один синий, то красных не более 17, а из любых 10 шаров найдется хотя бы один красный, то есть синих не более 9. Так как всех шаров 26, то синих – 9, а красных – 17.
Ответ. 70 кг
Решение. 5 процентов от 30 кг -  = 1,5 кг соли в 30кг морской воды,
= 1,5 кг соли в 30кг морской воды,
Х л добавили, стало (х+30)л. Х+30-100 процентов, 1,5 -1,5 процентов, тогда х=70
Ответ:  , k꞊1+5t, t
, k꞊1+5t, t
 .
.
Решение. tgx ctgx ꞊ sin5x
 ,
, 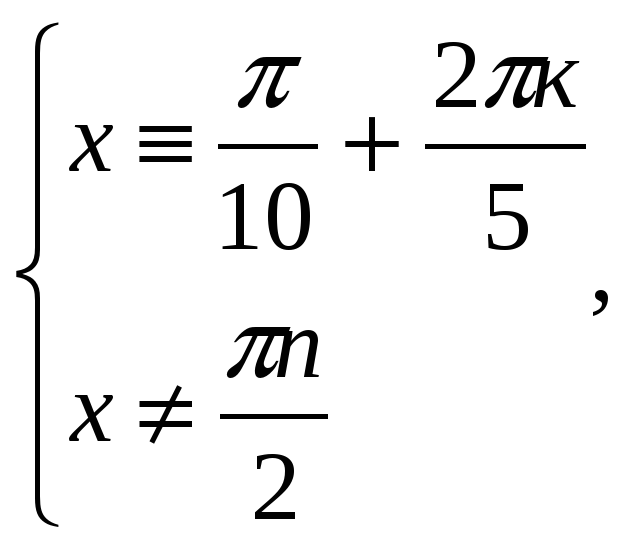 k
k
 , n
, n

Найдем теперь такие k, при которых  ꞊
꞊ . Это уравнение перепишем в виде 5n-4k꞊1.Частное решение последнего уравнения
. Это уравнение перепишем в виде 5n-4k꞊1.Частное решение последнего уравнения
n0꞊1, k0꞊1,тогда k꞊1+5t, t
 . Итак,
. Итак, 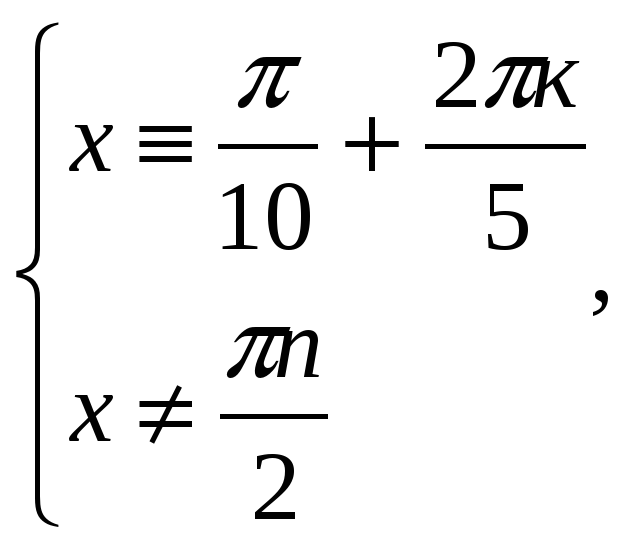 k
k
 , t
, t

Ответ:
Решение. Обозначим длину отрезка AB за 1, тогда SA=2. Найдём прежде всего длины отрезков BD и SD. Пусть BD=x. Тогда, применяя теорему Пифагора к треугольникам ABD и ASD, получаем AD²=1–x² = 4 – (2–x)², BD=x=1/2. Далее в треугольнике BMD BM꞊и, для того чтобы воспользоваться теоремой косинусов, достаточно найти косинус угла MBD. Но из прямоугольного треугольника SBM получаем: cos SBM ꞊
DM ² ꞊꞊, DM ꞊







 ху + z = 94,
ху + z = 94,
 ,
, 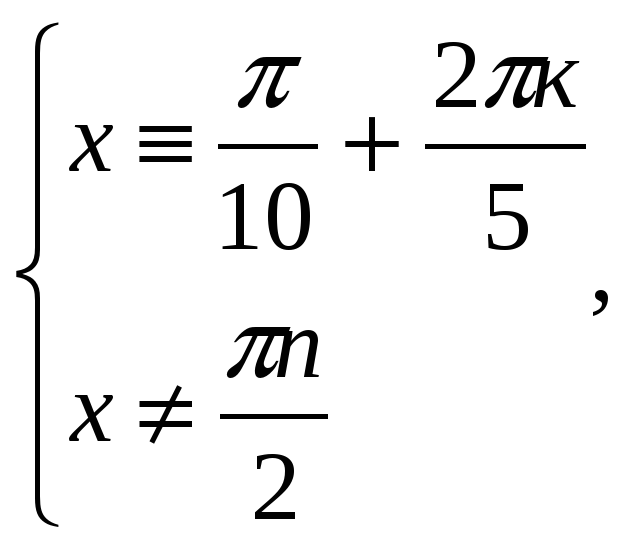 k
k









