Материальная точка движется прямолинейно по закону  (где
(где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени
— время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени  .
.
Материальная точка движется прямолинейно по закону  (где
(где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени
— время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени  .
.
Материальная точка движется прямолинейно по закону  , где
, где  — расстояние от точки отсчёта в метрах,
— расстояние от точки отсчёта в метрах,  — время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени
— время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени  .
.
Материальная точка движется прямолинейно по закону  , где
, где  — расстояние от точки отсчёта в метрах,
— расстояние от точки отсчёта в метрах,  — время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени
— время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени  .
.
Материальная точка движется прямолинейно по закону  (где
(где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени
— время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени  .
.
Материальная точка движется прямолинейно по закону  (где
(где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 6 м/с?
— время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 6 м/с?
Материальная точка движется прямолинейно по закону  (где
(где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 11 м/с?
— время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 11 м/с?







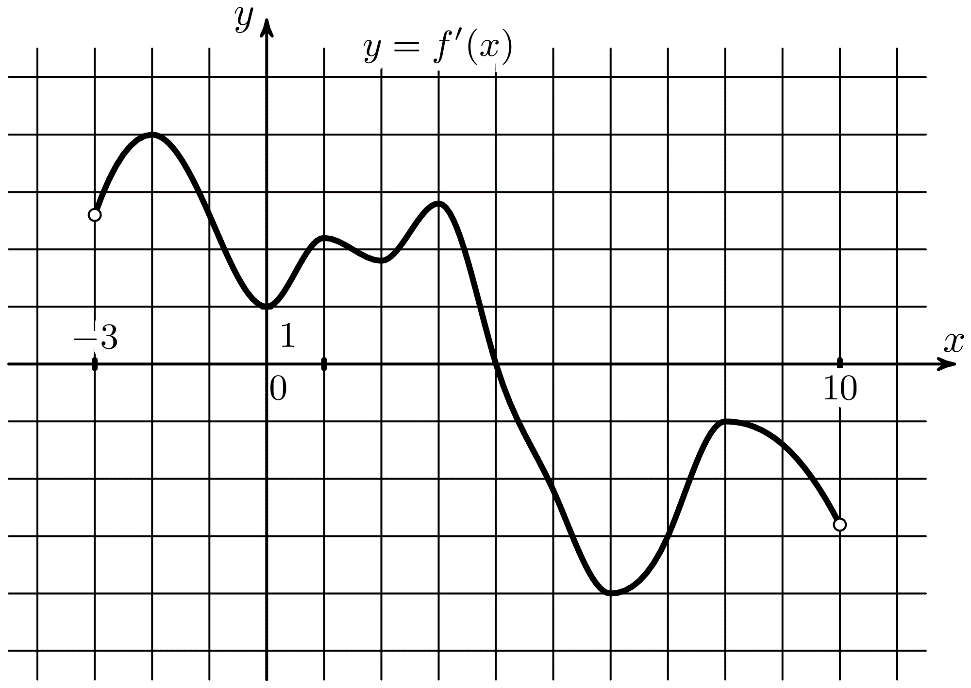
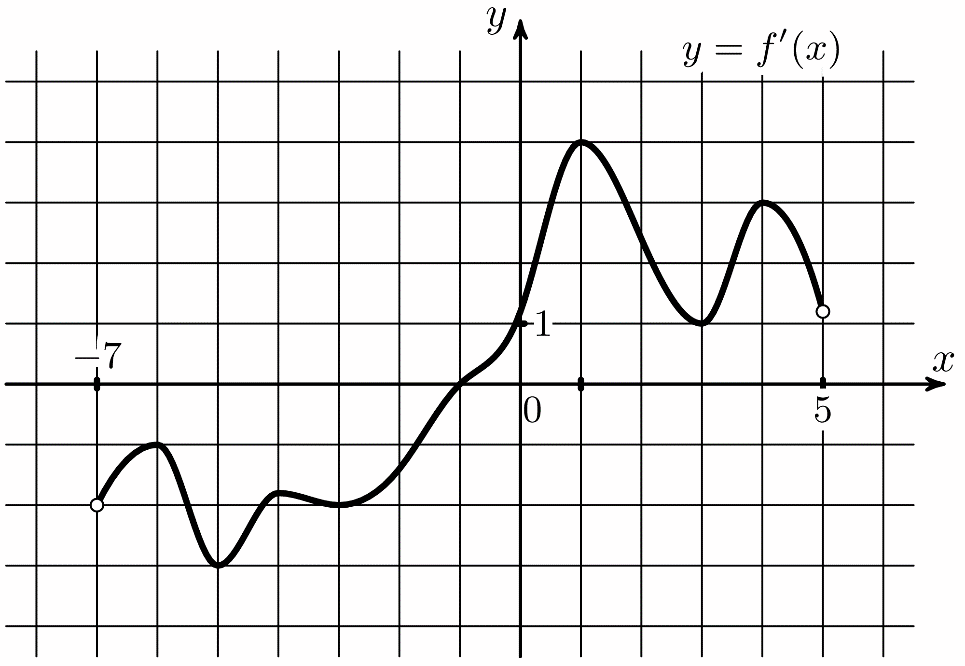
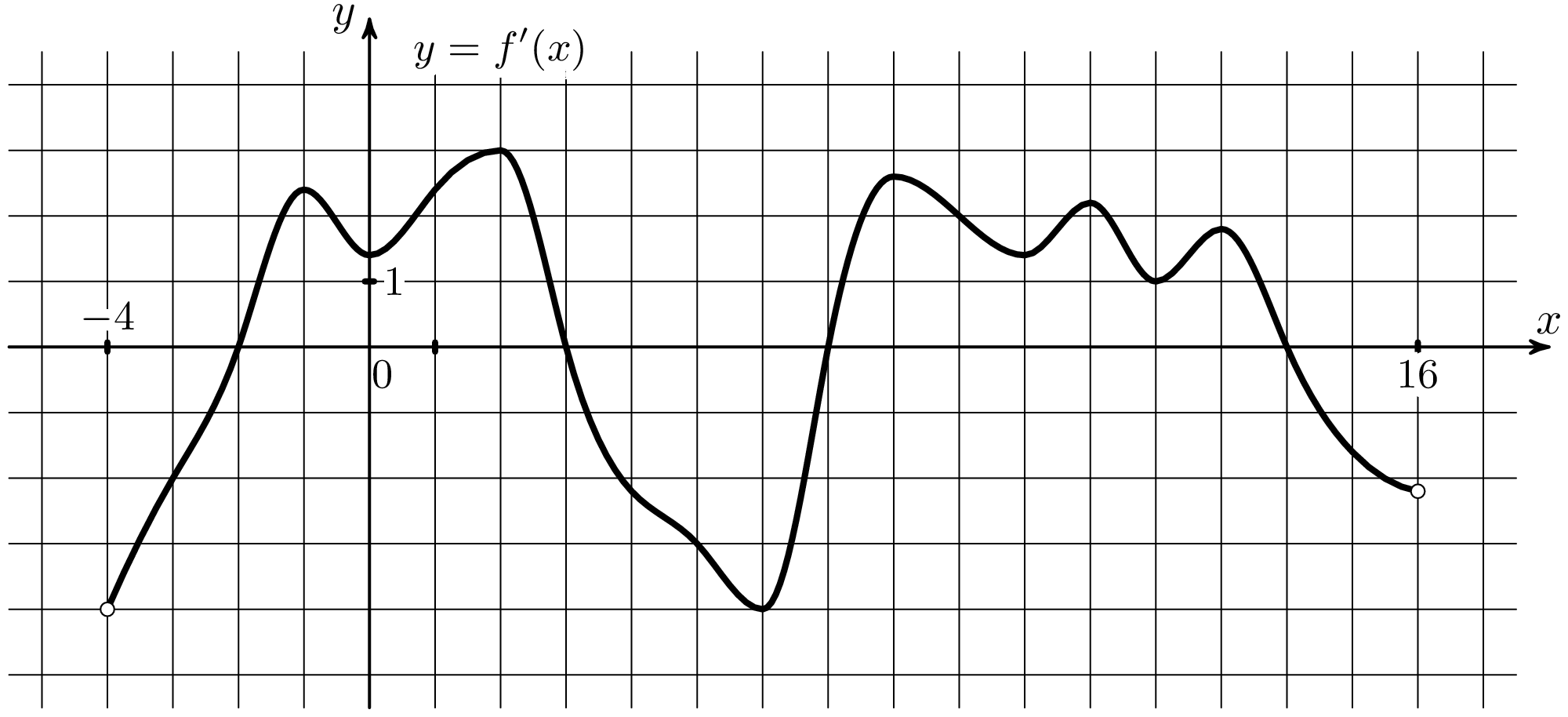
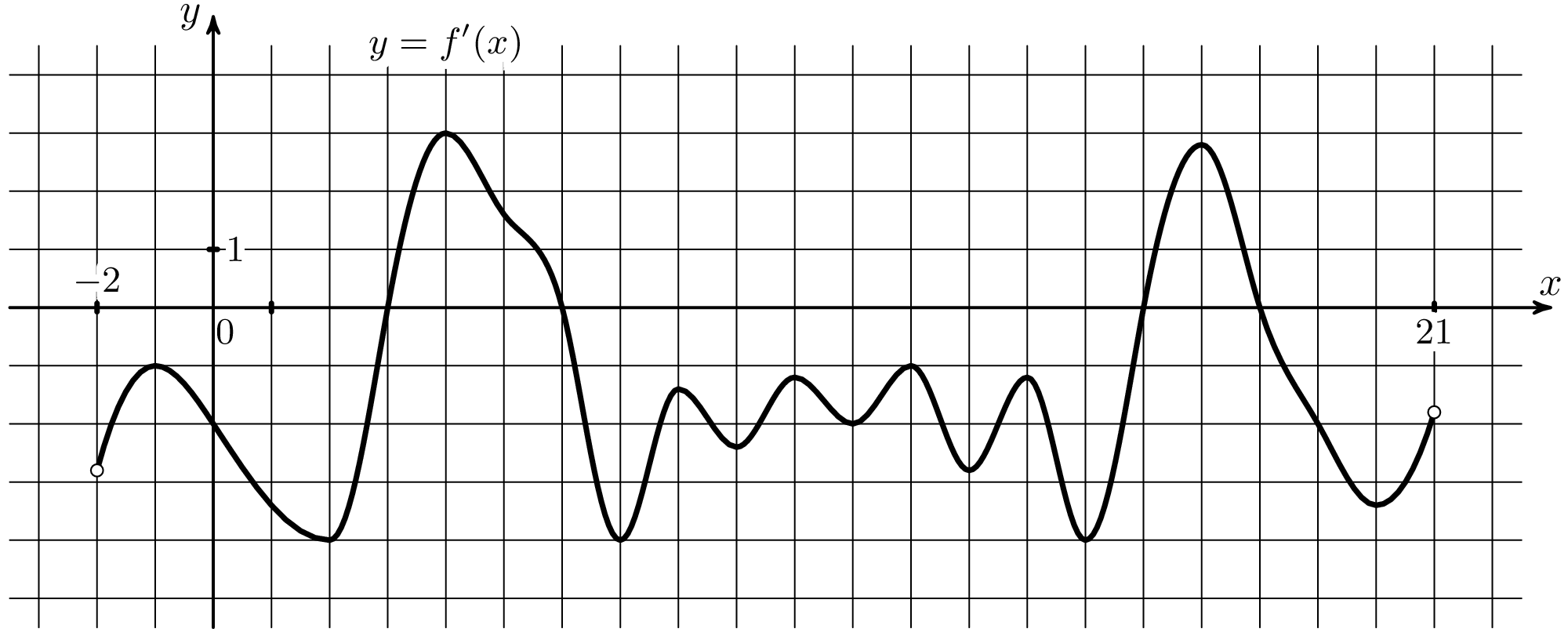
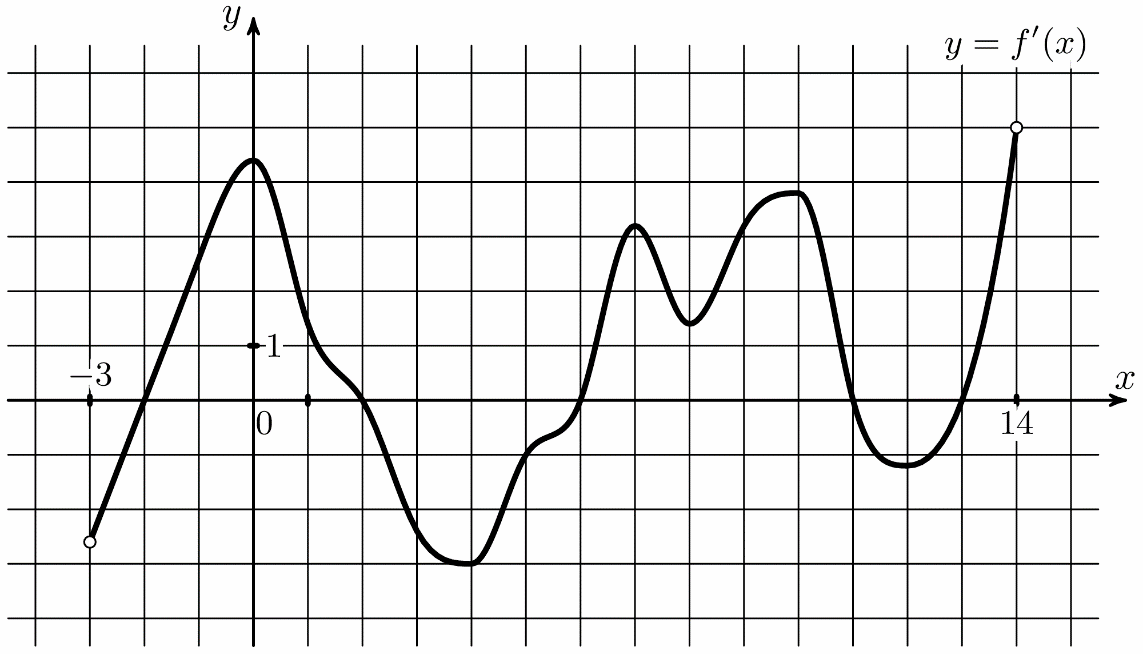


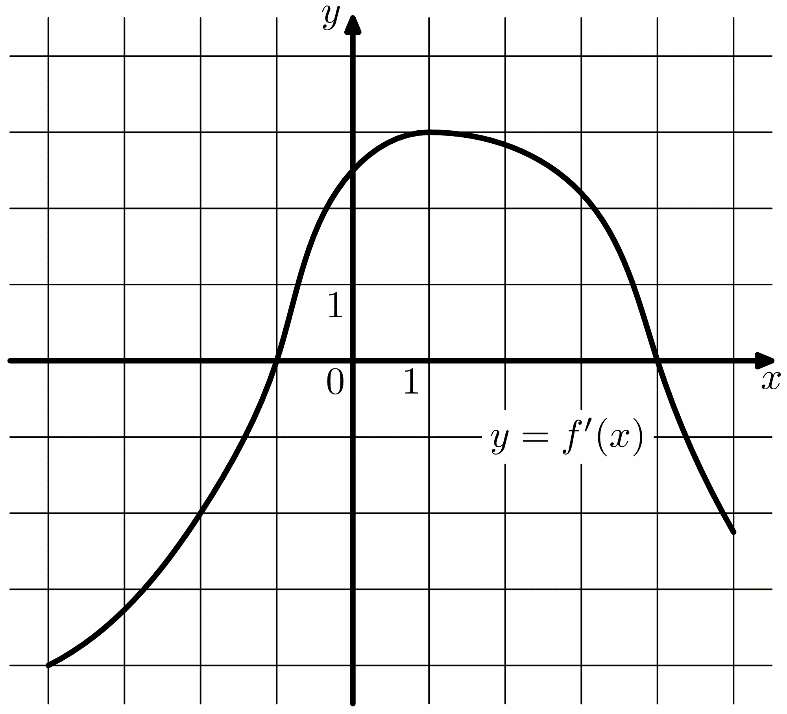

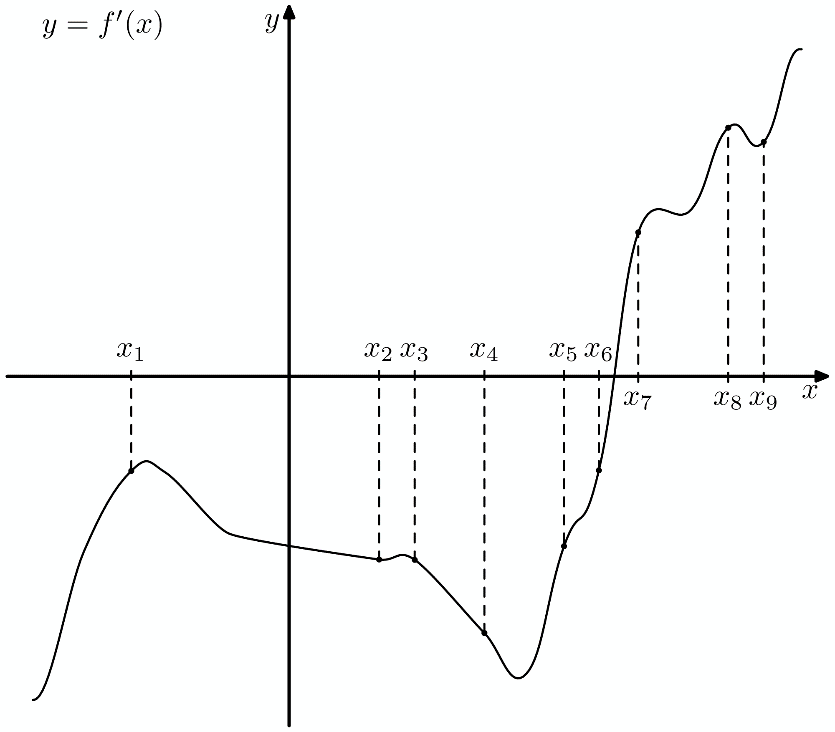

 (где
(где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени
— время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени  .
.
 .
. , где
, где  .
. , где
, где  .
. (где
(где 

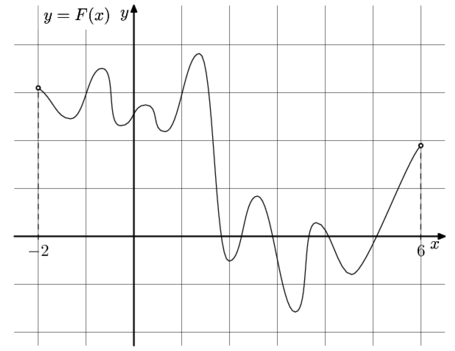
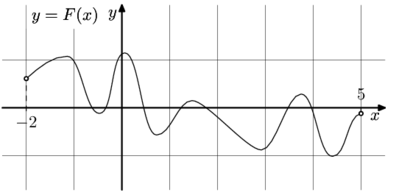
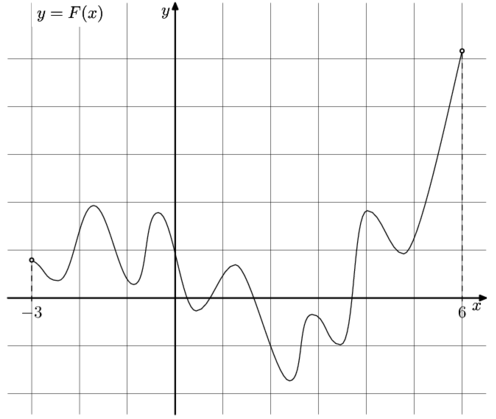
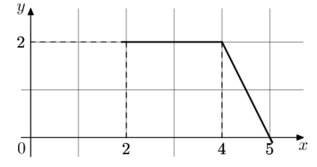


 – одна из первообразных функции
– одна из первообразных функции
 – одна из первообразных функции
– одна из первообразных функции 


 – одна из первообразных функции
– одна из первообразных функции
 – одна из первообразных функции
– одна из первообразных функции 
 – одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
– одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
 – одна из первообразных функции
– одна из первообразных функции












