Задание № 12 на ЕГЭ.
Найдите точку минимума функции
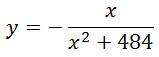
Решение:
Точка минимума функции – это точка экстремума функции, в которой производная меняет свой знак с отрицательного на положительный. Для вычисления точек экстремума необходимо найти производную функции и приравнять ее к нулю.
Область определения функции: все числа.
Найдем производную функции:
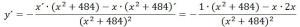

y´ = 0
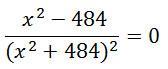
x2 — 484= 0
x1 = — 22
x2 = 22
Отметим точки – 22 и 22 на числовой прямой и найдем знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок)
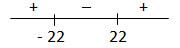
В точке x = 22 производная функции меняет знак с отрицательного на положительный, значит, это искомая точка минимума.
Ответ: 22
Задание.
Найдите наибольшее значение функции y = ln(x + 3)2 – 2x на отрезке [-2,5; 0]
Решение:
Найдем точку экстремума функции, для вычисления точек экстремума необходимо найти производную функции и приравнять ее к нулю.
Функция определена при x + 3 0, x — 3.
Упростим данную функцию:
y = 2ln(x + 3) – 2x
Найдем производную функции:
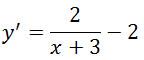
Найдем нули производной:
y′ = 0
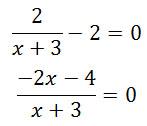
-2x – 4 = 0
x = — 2 принадлежит отрезу [-2,5; 0]
Отметим точки — 2,5; — 2 и 0 на числовой прямой и расставим знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок)
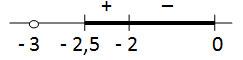
В точке х = — 2 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума на отрезке [-2,5; 0]. Найдем значение функции при x = — 2.
y(-2) = ln(-2 + 3)2 — 2·(-2) = ln1 + 4 = 4
Ответ: 4
Задание.
Найдите наибольшее значение функции
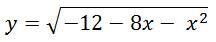
Решение:
Найдем точки экстремума, для этого найдем производную функции и приравняем ее к нулю.
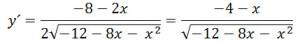
y´ = 0
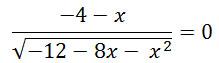
- 4 – x = 0
x = — 4
Получили единственную точку экстремума x = — 4, значение функции в данной точке будет наибольшим, найдем это значение:
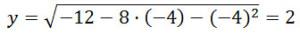
Наибольшее значение функции равно 2.
Ответ: 2
Задание.
Найдите точку минимума функции y = (6 – 4x)cosx + 4sinx + 6, принадлежащую промежутку (0; π/2).
Решение:
Точка минимума функции – это точка экстремума функции, в которой производная меняет свой знак с отрицательного на положительный. Для вычисления точек экстремума необходимо найти производную функции и приравнять ее к нулю.
Область определения функции: все числа, кроме 0.
Найдем производную функции:
y´ = (6 – 4x)´·cosx + (6 – 4x)·(cosx)´ + (4sinx)´
y´ = — 4cosx – (6 – 4x)sinx + 4cosx = – (6 – 4x)sinx
y´ = – (6 – 4x)sinx
y´ = 0
– (6 – 4x)sinx = 0
(6 – 4x)sinx
Произведение равно нулю тогда и только тогда, когда равен нулю хотя бы один из множителей, а другой при этом не теряет смысла, т.е.
6 – 4x = 0 и sinx = 0
Решим 1 уравнение:
6 – 4x = 0
x = 3/2
x = 1,5
Решим 2 уравнение:
sinx = 0
x = 0 не принадлежит промежутку (0; π/2)
Отметим точку x = 1,5 на числовой прямой, учитывая промежуток (0; π/2) и найдем знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок)
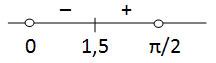
В точке x = 1,5 производная функции меняет знак с отрицательного на положительный, значит, это искомая точка минимума.
Ответ: 1,5
Задание.
Найдите наибольшее значение функции y = x3 — 6x2 + 9x + 5 на отрезке [0,5; 2].
Решение:
Функция определена на всей числовой прямой.
Найдем точки экстремума, для этого найдем производную функции и приравняем ее к нулю.
y´ = 3x2 — 12x + 9
y´ = 0
3x2 — 12x + 9 = 0
x2 — 4x + 3 = 0
D = 4
x1 = 3 не принадлежит отрезку [0,5; 2]
x2 = 1
Найдем значение функции в точке x = 1 и на границах отрезка [0,5; 2]:
y(0,5) = (0,5)3 — 6·(0,5)2 + 9·(0,5) + 5 = 8,125
y(1) = 13 — 6·12 + 9·1 + 5 = 9
y(2) = 23 — 6·22 + 9·2 + 5 = 7
Значит, набольшее значение функции равно 7
Ответ: 7
Задание.
Найдите наибольшее значение функции y = 13tgx – 13x + 5 на отрезке [-π/4; 0].
Решение:
Функция определена на промежутке (-π/2 + πn; π/2 + πn)
Найдем точки экстремума, для этого найдем производную функции и приравняем ее к нулю.
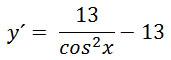
y´ = 0
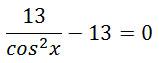
cos2x = 1
cosx = — 1 и cosx = 1
Решим 1 уравнение:
cosx = — 1
x = π не принадлежит отрезку [-π/4; 0].
Решим 2 уравнение:
cosx = 1
x = 0
Найдем значение функции в точке x = 0 и на границах отрезка [-π/4; 0]:
y(-π/4) = 13tg(-π/4) – 13·(-π/4) + 5 = 13π/4 — 8
y(0) = 13tg0 – 13·0 + 5 = 5
Значит, наибольшее значение функции равно 5
Ответ: 5
Задание.
Найдите наибольшее значение функции y = 11 + 24x – 2x√x на отрезке [63; 65].
Решение:
Функция определена на всей числовой прямой.
Найдем точки экстремума, для этого найдем производную функции и приравняем ее к нулю.
y´ = 24 — 3√x
y´ = 0
24 — 3√x = 0
√x = 8
x = 64
Найдем значение функции в точке x = 64 и на границах отрезка [63; 65]:
y(63) = 11 + 24·63 — 2·63·√63 ≈ 522,9
y(64) = 11 + 24·64 — 2·64·√64 = 523
y(65) = 11 + 24·65 — 2·65·√65 ≈ 522,9
Значит, наибольшее значение функции равно 523
Ответ: 523
Задание.
Найдите точку минимума функции
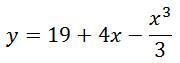
Решение:
Точка минимума функции – это точка экстремума функции, в которой производная меняет свой знак с отрицательного на положительный. Для вычисления точек экстремума необходимо найти производную функции и приравнять ее к нулю.
Функция определена на всей числовой прямой.
Найдем производную функции:
y´ = 4 – x2
y´ = 0
4 – x2 = 0
x1 = — 2, x2 = 2
Отметим точки – 2 и 2 на числовой прямой и найдем знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок)
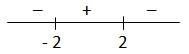
В точке x = — 2 производная функции меняет знак с отрицательного на положительный, значит, это искомая точка минимума.
Ответ: — 2
Задание.
Найдите наименьшее значение функции f(x) = e2x – 4ex + 7 на отрезке [-1; 1].
Решение:
Область определения функции: все числа
Найдем точки экстремума, для этого найдем производную функции и приравняем ее к нулю.
f´(x) = 2e2x – 4ex
f´(x) = 0
2e2x – 4ex = 0
2ex(ex – 2) = 0
Произведение равно нулю тогда и только тогда, когда равен нулю хотя бы один из множителей, а другой при этом не теряет смысла, т.е.
ex 0, ex – 2 = 0
ex – 2 = 0
ex = 2
x = ln2
Найдем значение функции в точке x = ln2 и на границах отрезка [-1; 1].
f(-1) = e-2 – 4e-1 + 7
f(ln2) = e2ln2 – 4eln2 + 7 = 4 – 8 + 7 = 3
f(1) = e2 – 4e + 7
Значит, наименьшее значение функции равно 3
Ответ: 3
Задание.
Найдите наименьшее значение функции y = (x – 10)2(x + 1) + 3 на отрезке [5; 14].
Решение:
Область определения функции: все числа
Найдем точки экстремума, для этого найдем производную функции и приравняем ее к нулю.
y´ = ((x – 10)2)´· (x + 1) + (x – 10)2·(x + 1)´ = 2(x – 10)· (x + 1) + (x – 10)2·1
y´ =(x – 10)·(2x + 2 + x – 10) = (x – 10)·(3x – 8)
y´ = 0
(x – 10)·(3x – 8) = 0
Произведение равно нулю тогда и только тогда, когда равен нулю хотя бы один из множителей, а другой при этом не теряет смысла, т.е.
x – 10 = 0 и 3x – 8 = 0
Решим 1 уравнение:
x – 10 = 0
x = 10
Решим 2 уравнение:
3x – 8 = 0
3x = 8
x = 8/3 не принадлежит отрезку [5; 14].
Найдем значение функции в точке x = 10 и на границах отрезка [5; 14].
y(5) = (5 – 10)2·(5 + 1) + 3 = 153
y(10) = (10 – 10)2·(10 + 1) + 3 = 3
y(14) = (14 – 10)2·(14 + 1) + 3 = 243
Значит, наименьшее значение функции равно 3
Ответ: 3
Задание.
Найдите наибольшее значение функции
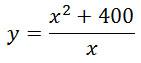 на отрезке [-28; -2].
на отрезке [-28; -2].
Решение:
Область определения функции: все числа, кроме 0.
Найдем точки экстремума, для этого найдем производную функции и приравняем ее к нулю.
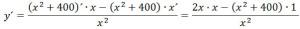
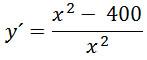
y´ = 0
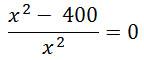
x2 – 400 = 0
x1 = — 20
x2 = 20 не принадлежит отрезку [-28; -2].
Найдем значение функции в точке x = — 20 и на границах отрезка [-28; -2].
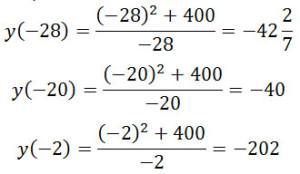
Значит, наибольшее значение функции равно: – 40
Ответ: - 40
Задание.
Найдите наименьшее значение функции y = (x – 22)ex-21 на отрезке [20; 22].
Решение:
Область определения функции: все числа
Найдем точки экстремума, для этого найдем производную функции и приравняем ее к нулю.
y´ = ex-21 + (x – 22)ex-21 = ex-21(1 + x – 22) = ex-21(x – 21)
y´ = 0
ex-21(x – 21) = 0
Произведение равно нулю тогда и только тогда, когда равен нулю хотя бы один из множителей, а другой при этом не теряет смысла, т.е.
ex-21 0,
x – 21 = 0
x = 21 ϵ [20; 22].
Найдем значение функции в точке x = 21 и на границах отрезка [20; 22]:
y(20) =(20 – 22)·e20-21 = — 2·e-2
y(21) =(21 – 22)·e21-21 = — 1
y(22) =(22 – 22)·e22-21 = 0
Значит, наименьшее значение функции равно: — 1.
Ответ: - 1
Задание.
Найдите наименьшее значение функции
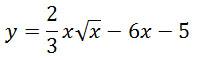 на отрезке [9; 36].
на отрезке [9; 36].
Решение:
Область определения функции [0; ∞)
Найдем точки экстремума, для этого найдем производную функции и приравняем ее к нулю.
y´ = √x – 6
Найдем нули производной:
y′ = 0
√x – 6 = 0
x = 36 ϵ [9; 36]
Найдем значение функции в точке x = 36 и на границах отрезка [9; 36]:
y(x) = 2/3·9·√9 — 6·9 – 5 = — 41
y(x) = 2/3·36·√36 — 6·36 – 5 = — 77
Значит, наименьшее значение функции равно – 77
Ответ: - 77
Задание.
Найдите наибольшее значение функции y = ln(x + 5)4 – 4x на отрезке [-4,5; 0]
Решение:
Найдем точку экстремума функции, для вычисления точек экстремума необходимо найти производную функции и приравнять ее к нулю.
Функция определена при x + 5 0, x — 5.
Упростим данную функцию:
y = 4ln(x + 5) – 4x
Найдем производную функции:
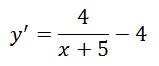
Найдем нули производной:
y′ = 0
- 4x – 16 = 0
- 4x = 16
x = — 4 принадлежит отрезу [-4,5; 0]
Отметим точки — 4,5; — 4 и 0 на числовой прямой и расставим знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок)
В точке х = — 4 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума на отрезке [-4,5; 0]. Найдем значение функции при x = — 4.
y(-4) = ln(-4 + 5)4 — 4·(-4) = ln1 + 16 = 16
Наибольшее значение функции можно находить другим способом, для этого нужно вычислить значения функции в точке х = — 4 и в граничных точках отрезка, имеем:
y(-4,5) = ln(-4,5 + 5)4 — 4·(-4,5) = 4ln(0,5) + 18 ≈ 14
y(0) = ln(0 + 5)4 — 4·0 = 4ln5 ≈ 8
y(-4) = ln(-4 + 5)4 — 4·(-4) = ln1 + 16 = 16
Ответ: 16
Задание.
Найдите точку максимума функции
y = (x – 5)2·ex – 7
Решение:
Точка максимума функции — это точка экстремума функции, в которой производная меняет свой знак с положительного на отрицательный. Для вычисления точек экстремума необходимо найти производную функции и приравнять ее к нулю.
Функция определена при x 0.
Найдем производную заданной функции:
y′ = 2(x – 5)·ex – 7 + (x – 5)2·ex– 7
Найдем нули производной:
y′ = 0
2(x – 5)·ex – 7 + (x – 5)2·ex– 7 = 0
ex – 7·(2x – 10 + x2 – 10x + 25) = 0
x2 – 8x + 15 = 0
x1 = 3 и x2 = 5
Отметим точки 3 и 5 на числовой прямой и расставим знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок)
В точке х = 3 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума.
Ответ: 3
Задание.
Найдите точку максимума функции
y = 1,5x2 – 39x + 120·lnx – 2.
Решение:
Точка максимума функции — это точка экстремума функции, в которой производная меняет свой знак с положительного на отрицательный. Для вычисления точек экстремума необходимо найти производную функции и приравнять ее к нулю.
Функция определена при x 0.
Найдем производную заданной функции:
Найдем нули производной:
y′ = 0
3x2 – 39x + 120 = 0
x2 – 13x + 40 = 0
x1 = 5 и x2 = 8
Отметим точки 5 и 8 на числовой прямой и расставим знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок)
В точке х = 5 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума.
Ответ: 5
Задание.
Найдите точку максимума функции y = — x/(x2 + 484)
Решение:
Точка максимума функции — это точка экстремума функции, в которой производная меняет свой знак с положительного на отрицательный. Для вычисления точек экстремума необходимо найти производную функции и приравнять ее к нулю.
Функция определена на всей числовой прямой.
Найдем производную заданной функции:
Найдем нули производной:
y′ = 0
x2 – 484 = 0
x1 = — 22; x2 = 22
Отметим точки — 22 и 22 на числовой прямой и расставим знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок)

В точке х = — 22 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума.
Ответ: — 22
Задание.
Найдите точку максимума функции y = -x/(x2 + 361)
Решение:
Точка максимума функции — это точка экстремума функции, в которой производная меняет свой знак с положительного на отрицательный. Для вычисления точек экстремума необходимо найти производную функции и приравнять ее к нулю.
Функция определена на всей числовой прямой.
Найдем производную заданной функции:
Найдем нули производной:
y′ = 0
x2 – 361 = 0
x1 = — 19; x2 = 19
Отметим точки — 19 и 19 на числовой прямой и расставим знаки производной функции на получившихся промежутках, подставляя любые значения из промежутков в найденную производную (см. рисунок)
В точке х = — 19 производная функции меняет знак с положительного на отрицательный, значит это искомая точка максимума.
Ответ: — 19







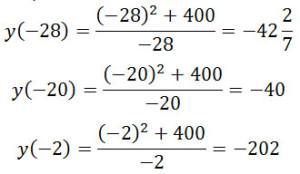








Электронная тетрадь по алгебре 10 класс...
Математика 6 класс
Алгебра 11 класс ФГОС
Алгебра 9 класс ФГОС
Электронная тетрадь по математике 5...
Наглядная геометрия 5-6 классы ФГОС
Геометрия 7 класс
Алгебра 11 класc
© 2017, Туля Татьяна Михайловна 3313 21
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы