
Исследовательская
работа на тему
Выполнил
Учени к 8 « Б » класса
МБОУ «Многопрофильный лицей»
Загоруйко Илья
Руководитель: Терентьева О.А.,
учитель математики
Математика в искусстве и живописи

Математика в искусстве
- В ХХI веке распространено заблуждение, что математика и искусство – не сочетаемые понятия.
- На самом же деле эти понятия неразделимо связаны друг с другом

Введение
Исторически, математика играла очень важную роль в музыке и изобразительном искусстве , в частности при изображении перспективы на плоском холсте или листе бумаги. Математика не играет очевидной роли в большинстве работ современного искусства. Однако было много художников, у которых математика находиться в центре внимания. Одним из них являлся Леонардо да Винчи. На искусство он смотрел не только глазами художника-творца, но и инженера, математика,провозглашая, что достоверности нет в науках там, где нельзя приложить, ни одной из математических наук . На уроках алгебры или геометрии нам не хватает времени, чтобы больше узнать о роли математических наук.. В результате мы часто задаёмся вопросом: «Зачем мы изучаем математику? Какое место в нашей жизни она занимает?»

Цель!
Целью работы является изучение связи между искусством и математическими науками.
В соответствии с поставленной целью решались следующие задачи :
Определить математических и музыкальных наук;
Рассмотреть несколько геометрических законов, содержащихся в живописи;
Понять важность математических законов и расчетов при построении архитектуры .

Математика в музыке
- Длины трех струн, дающих ноты до, ми, соль, которые составляют мажорный аккорд удовлетворяют арифметической пропорции

- В музыке немало математики . Мы используем западноевропейскую нотную систему, основа которой- две строгие шкалы частоты и времени .

Труды Пифагора
Первым ученым-математиком, отличившийся в музыкальной сфере, стал, несомненно, Пифагор. Он занимался поисками музыкальной гармонии, поскольку верил в то, что такая музыка необходима для очищения души и способна помочь разгадать любую тайну.
С помощью чаши с водой и однострунной арфы он изучил соотношения между высотой тона и числами. Он обнаружил, что половина длинны струны поднимает ноту на одну октаву вверх. Восемь звуков – до,ре,ми,фа,соль,ля,cи,до - древнейшая музыкальная гамма. Пифагорова теория музыки достигла даже небес. По мнению Пифагора каждая планета двигаясь с постоянной скоростью, проходит определённое расстояние, создавая звук. Именно благодаря трудам Пифагора математики обратили внимание на формальную сторону организации музыки- временную и частотную шкалы. С этого момента музыкальная и математическая науки пошли бок обок друг с другом. Более того музыка начала развиваться именно благодаря математике.

Геометрия на службе у живописи
- Линейная перспектива
- Симметрия и асимметрия
- Золотое сечение

Линейная перспектива
- Линейная прямая перспектива - вид перспективы, рассчитанный на фиксированную точку зрения и предполагающий единую точку схода на линии горизонта

Перспектива как наука возникла в глубокой древности в связи с необходимостью изображать на плоскости предметы в трехмерном пространстве и развивалась в двух направлениях: в области науки (строительстве, технике) и в живописи. История свидетельствует, что египетские пирамиды и храмы, величайшие сооружения Древней Греции и Рима были построены по изображениям - прототипам современных чертежей. Начала геометрии, и в частности перспективы, можно встретить в трудах древнегреческих и римских ученых.

Вывод
Закономерностями построения изображений окружающей действительности, близкой к зрительному восприятию, занимались и художники. Живопись древних времен не сохранилась, и неизвестно, какой она была в те далекие времена. Но высокое развитие архитектуры, скульптуры, дошедшей до наших дней, и труды древних ученых-математиков, писателей и философов дают основания предположить, что перспектива в творчестве художников занимала важное место.
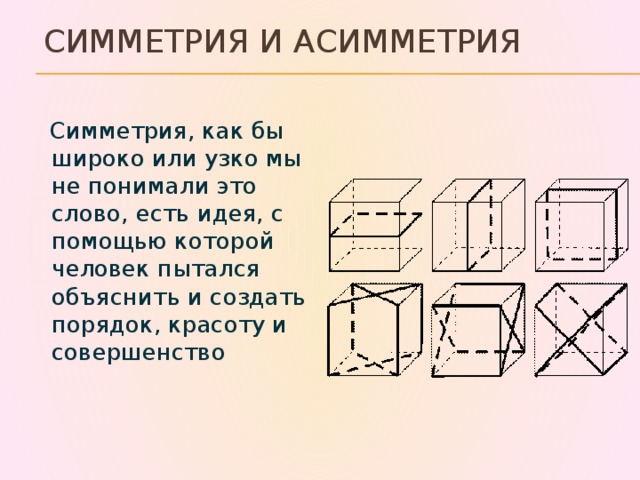
Симметрия и асимметрия
Симметрия, как бы широко или узко мы не понимали это слово, есть идея, с помощью которой человек пытался объяснить и создать порядок, красоту и совершенство

Симметрия
Еще одним фундаментальным понятием науки, которое наряду с понятием "гармонии" имеет отношение практически ко всем структурам природы, науки и искусства, является "симметрия". К фундаментальным понятиям симметрии относятся плоскость симметрии, ось симметрии, центр симметрии .
Плоскостью симметрии называется такая плоскость, которая делит фигуру на две зеркально равные части, расположенные друг относительно друга так, как предмет и его зеркальное отражение.
Осью симметрии называется такая прямая линия, вокруг которой симметричная фигура может быть повернута несколько раз таким образом, что каждый раз фигура "самосовмещается " сама с собой в пространстве. Число таких поворотов вокруг оси симметрии называется порядком оси.

Симметрия в кристаллах.
- Рассматривая различные кристаллы, мы видим, что все они разные по форме, но любой из них представляет симметричное тело. И действительно симметричность это одно из основных свойств кристаллов.

Определение
Асимметрия - это нарушение симметрии , соразмерности или ее отсутствие.
Асимметрия у камбалы возникла в результате эволюции при изменении условий жизни. Эта рыба ведет придонный образ жизни, поэтому глаза ее располагаются на одной стороне тела.

Асимметрия всегда придает пластической форме динамику и выявляет ее потенциальную способность к движению. Поэтому принципы асимметрии лежат в основе изображения предметов движущихся или имеющих какое-то отношение к движению, либо предметов, в которых надо выразить внутреннюю энергию, жизнь .
Благодаря асимметрии мышц, тело приобретает большее изящество

Асимметрия головного мозга
Правое полушарие отвечает за образное мышление , интуитивное, эмоциональное и обращено в прошлое. Функции правого - врожденные.
Л евое полушарие отвечает за абстрактное, интеллектуальное мышление . Функции левого полушария обращены в будущее. Однако мозг функционирует как единое целое

«Мир является бедным и бесплодным, без свободного и богатого разнообразия асимметрии» Аттирэ.

Ассиметричные здания

Золотое сечение
- Принято считать, что понятие о золотом сечении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.)

Определение
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b= b : c или с : b= b : а. Иоганн Кеплер говорил, что геометрия владеет двумя сокровищами: теоремой Пифагора и "Золотым сечением". О теореме Пифагора слышал каждый школьник, а о "Золотом сечении" - далеко не все.

Немного истории
В эпоху Возрождения золотое сечение было очень популярно среди художников, скульпторов и архитекторов. В большинстве живописных пейзажей линия горизонта делит полотно по высоте в отношении золотой пропорции, а при выборе размеров картин старались, чтобы отношение ширины к высоте тоже равнялось золотой пропорции.

Математика в архитектуре
- «Золотое сечение» многократно встречается при анализе геометрических соразмерностей Парфенона и Тадж-Махала

Храм Василия Блаженного
Известно, что принципы симметрии являются руководящими принципами для любого архитектора. В одних случаях архитектор ограничивается примитивной симметрией прямоугольного параллелепипеда, в других – использует более утонченную симметрию Асимметричное в целом сооружение может являть собой гармоничную композицию из симметричных элементов. Примером может служить собор Василия Блаженного на Красной площади в Москве. Нельзя не восхищаться этой причудливой композицией из десяти различных храмов.

Невозможные фигуры
- Невозможные фигуры - эти фигура, изображенная в перспективе таким способом, чтобы выглядеть на первый взгляд обычной фигурой. Однако при более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве.
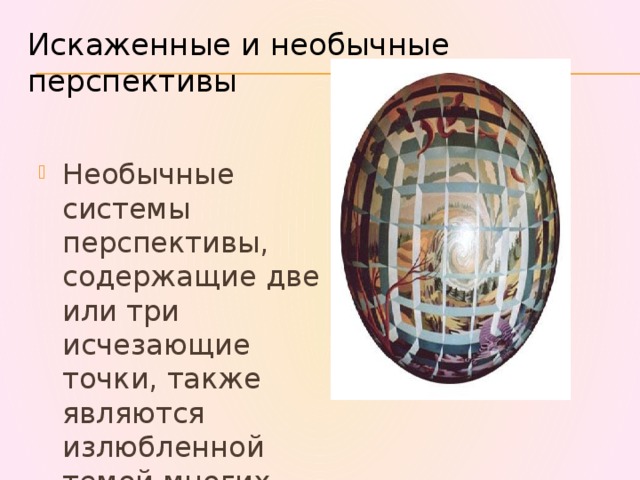
Искаженные и необычные перспективы
- Необычные системы перспективы, содержащие две или три исчезающие точки, также являются излюбленной темой многих художников.
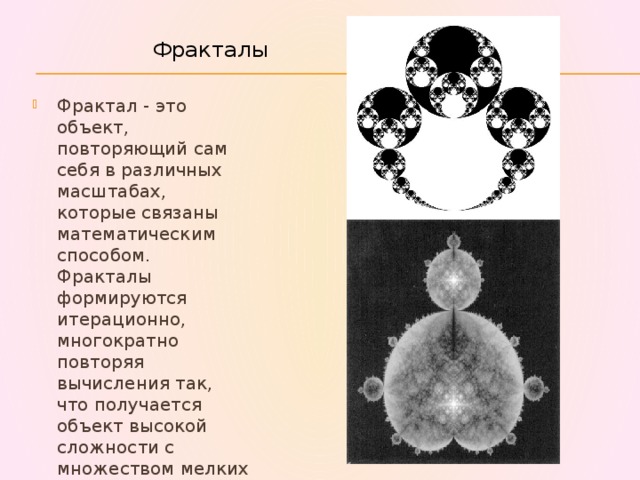
Фракталы
- Фрактал - это объект, повторяющий сам себя в различных масштабах, которые связаны математическим способом. Фракталы формируются итерационно, многократно повторяя вычисления так, что получается объект высокой сложности с множеством мелких деталей.

Заключение
- Настоящее искусство имеет свою теорию. Иногда эту теорию можно выразить в терминах математики, так как она тесно связана практически со всеми разновидностями современно искусства и искусства древних времен.
- Мы не осознаем, насколько наша жизнь связана с математикой. Даже такие творческие направления деятельности человека, как музыка, живопись, архитектура без математических законов не могут существовать и развиваться. В своей работе я постарался это показать и считаю, что моя работа дает более широкие представления о математике и ее использовании в разных областях деятельности человека и отвечает на вопрос: «Зачем изучать математику?»












































