Занятие кружка Квант от 30.09.19

Занятие кружка Квант от 30.09.19

1. Решите неравенство

2. Решите неравенство

3. Решите неравенство

4. Решите неравенство

5. Задание 19. а) Приведите пример числа-палиндрома, который делится на 15.

б) Сколько существует пятизначных чисел-палиндромов, делящихся на 15?

в) Найдите 37-е по величине число-палиндром, которое делится на 15.

4. Задание 16. Основание и боковая сторона равнобедренного треугольника равны 26 и 38 соответственно.

а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник.

б) Найдите длину отрезка этой средней линии, заключённого внутри окружности.

Задание 16. Основание и боковая сторона равнобедренного треугольника равны 34 и 49 соответственно.

а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник.

б) Найдите длину отрезка этой средней линии, заключённого внутри окружности.

5. Задание 19. Назовём натуральное число палиндромом, если в его десятичной записи все цифры расположены симметрично (совпадают первая и последняя цифры, вторая и предпоследняя, и т.д.). Например, числа 121 и 953359 являются палиндромами, а числа 10 и 953953 не являются палиндромами.

а) Приведите пример числа-палиндрома, которое делится на 45.

б) Сколько существует пятизначных чисел-палиндромов, делящихся на 45?

в) Найдите десятое по величине число-палиндром, которое делится на 45.

Задание 19. Назовём натуральное число палиндромом, если в его десятичной записи все цифры расположены симметрично (совпадают первая и последняя цифры, вторая и предпоследняя, и т.д.). Например, числа 121 и 953359 являются палиндромами, а числа 10 и 953953 не являются палиндромами.

а) Приведите пример числа-палиндрома, которое делится на 45.

б) Сколько существует пятизначных чисел-палиндромов, делящихся на 45?

в) Найдите десятое по величине число-палиндром, которое делится на 45.

Решение.

а) Самым простым вариантом будет число-палиндром 5445, которое делится на 45.

Ответ: 5445.

б) Разложим число 45 на простые множители, получим

,

то есть число должно делиться и на 5 и на 9. Признаком кратности числа на 5 является наличие цифры 5 в конце числа (цифру 0 не учитываем, т.к. она не подходит). Получаем число-палиндром в виде 5aba5, где a,b – цифры числа. Признаком делимости числа на 9 является то, что сумма цифр

должна делиться на 9. Из этого условия имеем:

- для b=0:  ;

- для b=1:  ;

- для b=2:  ;

- для b=3:  ;

- для b=4:  ;

- для b=5:  ;

- для b=6:  ;

- для b=7:  ;

- для b=8:  ;

- для b=9:  .

Таким образом, получаем 11 вариантов.

Ответ: 11 чисел.

в) Десятое по величине число-палиндром, делящийся на 45, равен 56565 - на самостоятельное решение.

Ответ: 56565.

Задание 19. а) Приведите пример числа-палиндрома, который делится на 15.

б) Сколько существует пятизначных чисел-палиндромов, делящихся на 15?

в) Найдите 37-е по величине число-палиндром, которое делится на 15.

Решение.

а) Число-палиндром – это число, которое остается неизменным, если его читать наоборот. Возьмем четырехзначное число-палиндром и составим его из цифр a и b, получим: abba. Нужно подобрать цифры a и b так, чтобы число abba делилось на 15, т.е. оно должно быть кратно 15. Чтобы число было кратно 15, цифра a должна быть равна 5. Остается подобрать цифру b так, чтобы число было кратно 15, получим:

- число 5115 – кратно 15;

- число 5225 – не кратно 15;

- число 5335 – не кратно 15;

- число 5445 – кратно 15;

и т.д.

Ответ: 5115; 5445.

б) Чтобы число делилось на 15, последняя цифра должна быть 5 (0 на конце недопустим), получим числа по форме 5aba5. Также это число должно делиться еще и на 3, т.к.  , где 3 и 5 – простые числа. Признаком делимости числа на 3 является то, что сумма цифр числа делится на 3, таким образом, получаем условие:

должно быть кратно 3. Очевидно, цифра b может быть от 0 до 9, имеем:

- для b=0:  ;

- для b=1:  ;

- для b=2:  ;

- для b=3:  .

Дальше все повторяется, т.к. сумма увеличилась на 3. Таким образом, в первой тройке значений имеем 10 вариантов чисел-палиндромов. Аналогично для второй и третьей тройки. В последнем варианте при b=9 имеем 3 варианта и того 30+3=33 варианта.

Ответ: 33.

в) Найдем 37-е по счету число-палиндром, начиная с самого младшего, т.е. с трехзначного числа типа 5a5, затем переберем четырехзначные 5aa5, получим:

- для трехзначных:

525, 555, 585;

- для четырехзначных:

5115, 5445, 5775;

Итак, имеем 6 первых чисел-палиндромов. В соответствии со схемой, представленной в пункте б), найдем 37-е число-палиндром. По сути, нужно найти 37-6=31-е пятизначное число-палиндром, которое будет соответствовать b=2 и a=9, т.е. получим число  

59295

Ответ: 59295.

Задание 16. Основание и боковая сторона равнобедренного треугольника равны 26 и 38 соответственно.

а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник.

б) Найдите длину отрезка этой средней линии, заключённого внутри окружности.

Решение.

а) В равнобедренном треугольнике ABC стороны AB=AC=38, а основание BC=26. Вписанная окружность с центром в точке O пересекает среднюю линию MN в точке P и Q и высоту AH в точке K. Сторон треугольника окружность касается в точках D, E и H, то есть, отрезки OD=OE=OH=r.

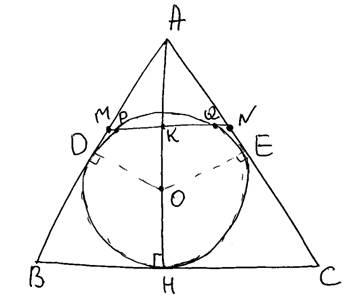
Так как MN – средняя линия, то  ,  . Рассмотрим прямоугольный треугольник AHB (так как AH – высота). В соответствии с теоремой Пифагора, имеем:

Сторона   (так как MN – средняя линия). Выразим радиус r окружности через площадь треугольника ABC:

,

где p – полупериметр треугольника, откуда

.

Также, площадь треугольника ABC равна

Таким образом,

,

а  . Заметим, что длина отрезка   и это значит, что

,

то есть окружность пересекает среднюю линию MN.

б) Требуется найти длину отрезка PQ (см. рисунок). Точки M и N средней линии MN лежат в центрах отрезков AB и AC соответственно. То есть,  . По теореме о касательных к окружности AD=AE, BD=BH, CE=CH и периметр треугольника ABC:

Отсюда

(MD – касательная к окружности, MN – секущая). По теореме о касательной и секущей, имеем:

Подставим в (*) значения MP и MQ, получим:

Ответ: 5.

Задание 16. Основание и боковая сторона равнобедренного треугольника равны 34 и 49 соответственно.

а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник.

б) Найдите длину отрезка этой средней линии, заключённого внутри окружности.

Решение.

а) Пусть О — центр окружности, вписанной в треугольник ABC со сторонами АВ = АС = 49, ВС = 34, АН — высота треугольника, точки М и N — середины сторон АВ и АС соответственно, K — точка пересечения АН и MN, p — полупериметр треугольника ABC. Поскольку MN — средняя линия равнобедренного треугольника, точка K — общая середина MN и АН.

Из прямоугольного треугольника АВН находим, что

,

значит,  .

Пусть r — радиус вписанной окружности треугольника ABC. Тогда

,

а диаметр вписанной окружности равен  . Очевидно,  , значит  .

Следовательно, вписанная окружность пересекает среднюю линию MN треугольника.

б) Пусть вписанная окружность касается сторон АВ и АС в точках D и Е соответственно, а средняя линия MN пересекает эту окружность в точках Р и Q (Р между М и Q). Тогда

По теореме о касательной и секущей  , а так как

то  . Отсюда находим, что PQ = 8.

Ответ: 8.