Занятие математического кружка
«Теорема Вариньона, ее применение при решении геометрических задач»
В школьном курсе геометрии рассматривается достаточное количество теории и решается множество задач по четырехугольникам. Возможно, этого объема теоретического материала вполне достаточно для решения школьных задач и без знания теоремы Вариньона, но, используя эту теорему, наше решение может быть более компактным и интересным. Но, к сожалению, в школьном курсе не рассматривается такой простой и интересный факт, что фигура, полученная последовательным соединением середин сторон произвольного четырехугольника, является параллелограммом , но я считаю изучение этой теоремы необходимым.
Теорема Вариньона поразила меня своей простотой, очевидностью, помогла разглядеть те удивительные факты, которые были для меня раньше незаметны.

Пьер Вариньон родился во Франции в 1654 году. Обучался в иезуитском коллеже и университете в Кане, где стал магистром в 1682 году. Он готовился к религиозной деятельности, но, изучая сочинения Эвклида и Декарта, увлекся математикой и механикой. Труды Вариньона посвящены теоретической механике, анализу бесконечно малых, геометрии, гидромеханике. Наибольшее значение имеют работы Вариньона по геометрической статике. В 1687 г. в работе «Проект новой механики...» Вариньон дал чёткую формулировку закона параллелограмма сил, развил понятие момента сил. С 1688 г. член Парижской Академии наук, работал профессором математики в коллеже Мазарини. Пьер Вариньон, руководил «Журналом учёных» в Париже и написавший учебник по элементарной геометрии, первым заострил внимание на, казалось бы, довольно очевидном факте: середины сторон выпуклого четырёхугольника являются вершинами параллелограмма.
Теорема Вариньона и выпуклые четырехугольники.
Следствия из теоремы.
Т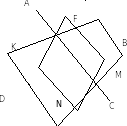 еорема. Середины сторон произвольного четырёхугольника являются вершинами параллелограмма, площадь равна половине площади данного четырехугольника.
еорема. Середины сторон произвольного четырёхугольника являются вершинами параллелограмма, площадь равна половине площади данного четырехугольника.
Дано: АВСD- выпуклый четырехугольник,
F,M,N,K-середины сторон AB, BC,CD, AD
Доказать: FMNK параллелограмм
Доказательство: FM и KN – средние линии соответственно треугольника ABC и треугольника ACD. Следовательно
KN || AC, KN = 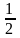 AC; FM|| AC, FM=
AC; FM|| AC, FM= 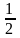 AC, значит KN || FM, KN=FM. Тогда делаем вывод, что FMNK – параллелограмм.
AC, значит KN || FM, KN=FM. Тогда делаем вывод, что FMNK – параллелограмм.
Площадь параллелограмма равна половине площади исходного четырёхугольника.
Доказать: 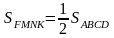
Доказательство: Обозначим площадь четырехугольника ABCD через S.
Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника,
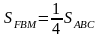 ,
, 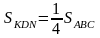

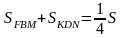 Аналогично рассуждая, получаем:
Аналогично рассуждая, получаем: 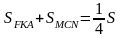 Следовательно:
Следовательно: 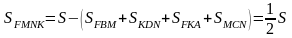
Параллелограмм, образованный серединами сторон, иногда называется параллелограмма Вариньона.
Периметр параллелограмма Вариньона равен сумме диагоналей исходного четырёхугольника.
Бимедианы четырехугольника– это отрезки, соединяющие середины противоположных сторон (диагонали параллелограмма Вариньона)
Справедливость теоремы Вариньона не зависит от выпуклости четырёхугольника. Теорема Вариньона и следствие из неё остаются верными и для невыпуклого четырехугольника
Следствия из теоремы.
1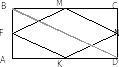 . Середины сторон прямоугольника являются вершинами ромба.
. Середины сторон прямоугольника являются вершинами ромба.
Доказательство: Диагонали прямоугольника равны, то есть AC=BD значит FM=KN=MN=FK, тогда FMNK – ромб.

2. Середины сторон равнобедренной трапеции являются вершинами ромба.
Доказательство: Диагонали равнобедренной трапеции равны, то есть BD=AC , тогда FM=KN=MN=FK, следовательно, FMNK – ромб.
3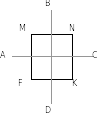 . Середины сторон ромба являются вершинами прямоугольника.
. Середины сторон ромба являются вершинами прямоугольника.
Доказательство: Диагонали ромба взаимно перпендикулярны, то есть ACBD , а так как MN||AC, FK||AC , FM||DB , NK||DB ,то FMNK – прямоугольник.
Подводя итоги кратко можно сказать:
1) Если ABCD – прямоугольник, то KLMN – ромб;
2) Если ABCD - ромб, то KLMN – прямоугольник;
3) Если ABCD – равнобедренная трапеция, то KLMN - ромб.
Применение теоремы Вариньона к доказательству некоторых утверждений
В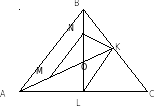 учебнике геометрии Атанасяна Л.С рассматривается доказательство теоремы об основном свойстве медиан треугольника, продемонстрируем применение теоремы Вариньона к доказательству этой теоремы
учебнике геометрии Атанасяна Л.С рассматривается доказательство теоремы об основном свойстве медиан треугольника, продемонстрируем применение теоремы Вариньона к доказательству этой теоремы
B
![]()
Теорема. Медианы в треугольнике пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.
Доказательство: проведём две медианы AK и BL треугольника ABC. Пусть О – точка их пересечения. Середины сторон невыпуклого четырехугольника АCBО – точки K, L, M и N– вершины параллелограмма, причем точкой пересечения его диагоналей KM и LN для этой конфигурации будет точка пересечения медиан О. Итак, AM = MO = OK и BN = NO = OL, т.е. точка О делит каждую из медиан AK и BL в отношении 2:1.Аналогично доказывается для медианы, проведённой из вершины С.
Утверждение 1. В выпуклом четырехугольнике сумма квадратов диагоналей в 2 раза больше суммы квадратов отрезков соединяющих середины противоположных сторон.
Д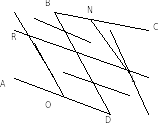 оказательство: Так как ORNL– параллелограмм, а сумма квадратов его сторон равна сумме квадратов его диагоналей, то
оказательство: Так как ORNL– параллелограмм, а сумма квадратов его сторон равна сумме квадратов его диагоналей, то 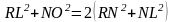
Так как 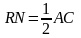 ,
,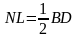 , то получаем:
, то получаем:
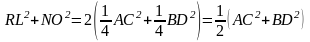
У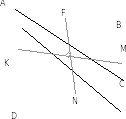 тверждение 2. Если отрезки соединяющие середины противоположных сторон выпуклого четырехугольника равны, то диагонали четырехугольника перпендикулярны.
тверждение 2. Если отрезки соединяющие середины противоположных сторон выпуклого четырехугольника равны, то диагонали четырехугольника перпендикулярны.
Доказательство: Так как 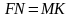 , но FN и MK являются диагоналями параллелограмма FMNK, тогда FMNK – прямоугольник, стороны которого параллельны диагоналям четырехугольника ABCD значит BDAC.
, но FN и MK являются диагоналями параллелограмма FMNK, тогда FMNK – прямоугольник, стороны которого параллельны диагоналям четырехугольника ABCD значит BDAC.
У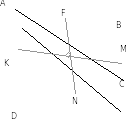 тверждение 3. Если отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, перпендикулярны, то диагонали четырехугольника равны.
тверждение 3. Если отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, перпендикулярны, то диагонали четырехугольника равны.
Доказательство: Так как FNMK и FMNK – параллелограмм, то FMNK –ромб, то есть FM=MN=NK=FK значит AC=BD
Применение теоремы Вариньона к решению задач
Рассмотрим задачи, которые встречаются в школьном курсе геометрии.
Учебник для 7 – 11 классов средней школы. Погорелов А. В.
Задача 55, стр100. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма
Доказательство: Полученный четырехугольник является параллелограммом по теореме Вариньона
Задача 57, стр100. У четырехугольника диагонали равны a и b. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Решение: Полученный четырехугольник является параллелограммом по теореме Вариньона. Периметр параллелограмма Вариньона равен сумме диагоналей исходного четырёхугольника т.е. a+b.
Задача 58, стр100 .Докажите, что середины сторон прямоугольника являются вершинами ромба. И наоборот, середины сторон ромба являются вершинами прямоугольника
Доказательство: Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба (следствие 1);
Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба ( следствие 3).
Учебник для 7 – 9 классов общеобразовательных учреждений В.Н.Руденко, Г.А.Бахурин
Задача 374. Докажите, что середины сторон параллелограмма являются вершинами нового параллелограмма
Доказательство: Новый четырехугольник является параллелограммом по теореме Вариньона
Задача 413. Диагональ квадрата равна 7см. найдите периметр четырехугольника, вершинами которого являются середины сторон квадрата
Решение: Полученный четырехугольник является квадратом. Периметр по следствиям из теоремы Вариньона равен a+b, где a и b являются диагоналями исходного четырехугольника у квадрата диагонали равны, значит периметр равен 14см.
Учебник для 7 – 11 классов средней школы. Г.П.Бевз, В.Г.Бевз, Н.Г.Владимирова
Задача 369. Какую форму имеет четырехугольник, вершинами которого являются середины сторон прямоугольника?
Решение: Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба (следствие 1);
Задача 371. Докажите, что средние линии четырехугольника делятся точкой пересечения пополам.
Доказательство: Т.к. средние линии четырехугольника являются диагоналями параллелограмма Вариньона, то точка пересечения делит их пополам.
Р ассмотрим задачи на бимедианы четырехугольника и теорему Вариньона, которые взяты с различных математических конкурсов и олимпиад.
ассмотрим задачи на бимедианы четырехугольника и теорему Вариньона, которые взяты с различных математических конкурсов и олимпиад.
З адача 1. Докажите, что если диагонали четырехугольника равны, то его площадь равна произведению средних линий
Дано: ABCD – четырехугольник; AC = BD
Доказать: SABCD = KM*LN
Доказательство:
Доказательство: KLMN – параллелограмм Вариньона. Так как AC= BD, параллелограмм Вариньона является ромбом. SKMNL =KM*LN /2 (площадь ромба равна половине произведения его диагоналей ).
SABCD = 2 SKMNL = KM * LN
Задача 2. Докажите, что площадь параллелограмма, образованного прямыми, проходящими через вершины выпуклого четырехугольника и параллельными его диагоналям, в два раза больше площади исходного четырехугольника
Доказательство:
SABCD=SLMNK+SLKD+SALM+SBMN+SKCN
Так как AMOL, MONB, CKON, DKOL - параллелограммы,
То SALM=SMOL , SMBN=SMON, SNCK=SKON . SLKD=SLOK
Отсюда получаем, что SABCD=2SKLMN
З адача 3.Доказать, что периметр параллелограмма Вариньона равен сумме длин диагоналей четырехугольника ABCD.
Доказательство:
Так как KL=MN=1/2 AC
LM=KN=1/2 BD
(как средние линии треугольниковABC и BCD),
то: PKLMN=2*(KL+LM)=2*(1/2AC+1/2BD)
=AC+BD.
PKLMN=AC+BD.
З адача 4. Отрезки, соединяющие середины противоположных сторон четырехугольника, называются средними линиями. Доказать, что средние линии четырехугольника точкой пересечения делятся пополам.
Доказательство:
Поскольку средние линии
KM и LN четырехугольника
ABCD являются диагоналями
параллелограмма Вариньона,
то точка пересечения делит их пополам (по свойству диагоналей параллелограмма) KM и LN - средние линии четырехугольника ABCD.
Задача 5 .
П равильно ли, что можно составить треугольник из любой средней линии четырехугольника и отрезков, вдвое меньших от его диагоналей?
Решение:
Правильно, так как параллелограмм
Вариньона существует
для произвольного
выпуклого четырехугольника.
Например, условие задачи
удовлетворяют треугольники KLM и LMN.
B  : KL-средняя линия ABCD, KL=1/2AC, LM=1/2BD.
: KL-средняя линия ABCD, KL=1/2AC, LM=1/2BD.
З адача6 . Построить ромб с вершинами на сторонах прямоугольника ABCD
Доказательство: Поскольку диагонали AB и CD прямоугольника равны,
то параллелограмм Вариньона KLMN и
будет искомым ромбом для прямоугольника
ABCD. KL =1/2AC, LM=1/2BD;При этом AC=BD.
Отсюда, KL=LM=MN=NK. Итак, KLMN-ромб.
KLMN- ромб с вершинами в серединах сторон четырехугольника ABCD.
З адача7. Пусть L и N – середины противоположных сторон BC и AD четырехугольника ABCD. Доказать, что площадь четырехугольника LPNQ равна сумме площадей треугольников ABP и CQD.
Доказательство:
SALCN = SNBLD = .
.
В треугольнике
ACD медиана CN делит его на два треугольника равной площади, а в треугольнике ABC медиана AL делит его на два равновеликих треугольника. Так как SABC+SACD=SABCD ,то SALCN=SNBLD= . аналогично устанавливается нужное равенство и для четырехугольника NBLD. Теперь утверждение задачи следует из того, что четырехугольники ALCN и NBLD покрывают внутри четырехугольника ABCD два раза четырехугольник LPNQ и не покрывают треугольники ABP и CQD, а их сумма их площадей равна площади четырехугольника ABCD. Площадь четырехугольника, с другой стороны, равна сумме площадей шести треугольников (в том числе и треугольников ABP и CQD) и интересующего нас четырехугольника LPNQ.
. аналогично устанавливается нужное равенство и для четырехугольника NBLD. Теперь утверждение задачи следует из того, что четырехугольники ALCN и NBLD покрывают внутри четырехугольника ABCD два раза четырехугольник LPNQ и не покрывают треугольники ABP и CQD, а их сумма их площадей равна площади четырехугольника ABCD. Площадь четырехугольника, с другой стороны, равна сумме площадей шести треугольников (в том числе и треугольников ABP и CQD) и интересующего нас четырехугольника LPNQ.
.Литература
1.Адмар Ж. Элементарная геометрия, М., Учпедгиз, 1948.
2.Кокстер Г., Грейтцер С. Новые встречи с геометрией. М., 1978.
3. Геометрия. Учебник для 7 – 9 классов общеобразовательных учреждений
Л. С. Атанасян, В.Ф. Бутузов, С. Б. Кадомцев и др, – М.: Просвещение,2012.
4. Геометрия. Учебник для 7 – 11 классов средней школы. Погорелов А. В - М.: Просвещение.2012
5. Геометрия. Учебник для 7 – 11 классов средней школы. Г.П.Бевз, В.Г.Бевз, Н.Г.Владимирова- М.: Просвещение.2011
6. Геометрия. Учебник для 7 – 9 классов общеобразовательных учреждений В.Н.Руденко, Г.А.Бахурин - М.: Просвещение.2001
7.Сборник тестовых заданий по геометрии 9 класс, «Интеллект-Центр» Москва 2001
8.Задачи по геометрии 7-11кл., авторы: Б. Г. Зив, В. М. Мейлер, А. Г. Баханский.
Интернет источники
1.https://ru.wikipedia.org/wiki/Теорема_Вариньона_(геометрия)
2. https://yadi.sk/i/Q3GSNIImfTxf5
11








 еорема. Середины сторон произвольного четырёхугольника являются вершинами параллелограмма, площадь равна половине площади данного четырехугольника.
еорема. Середины сторон произвольного четырёхугольника являются вершинами параллелограмма, площадь равна половине площади данного четырехугольника.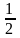 AC; FM|| AC, FM=
AC; FM|| AC, FM= 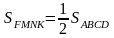
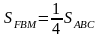 ,
, 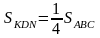

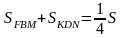 Аналогично рассуждая, получаем:
Аналогично рассуждая, получаем: 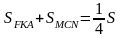 Следовательно:
Следовательно: 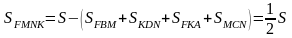
 . Середины сторон прямоугольника являются вершинами ромба.
. Середины сторон прямоугольника являются вершинами ромба.
 . Середины сторон ромба являются вершинами прямоугольника.
. Середины сторон ромба являются вершинами прямоугольника. учебнике геометрии Атанасяна Л.С рассматривается доказательство теоремы об основном свойстве медиан треугольника, продемонстрируем применение теоремы Вариньона к доказательству этой теоремы
учебнике геометрии Атанасяна Л.С рассматривается доказательство теоремы об основном свойстве медиан треугольника, продемонстрируем применение теоремы Вариньона к доказательству этой теоремы  оказательство: Так как ORNL– параллелограмм, а сумма квадратов его сторон равна сумме квадратов его диагоналей, то
оказательство: Так как ORNL– параллелограмм, а сумма квадратов его сторон равна сумме квадратов его диагоналей, то 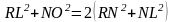
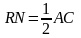 ,
,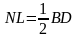 , то получаем:
, то получаем: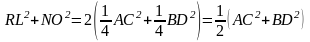
 тверждение 2. Если отрезки соединяющие середины противоположных сторон выпуклого четырехугольника равны, то диагонали четырехугольника перпендикулярны.
тверждение 2. Если отрезки соединяющие середины противоположных сторон выпуклого четырехугольника равны, то диагонали четырехугольника перпендикулярны.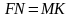 , но FN и MK являются диагоналями параллелограмма FMNK, тогда FMNK – прямоугольник, стороны которого параллельны диагоналям четырехугольника ABCD значит BDAC.
, но FN и MK являются диагоналями параллелограмма FMNK, тогда FMNK – прямоугольник, стороны которого параллельны диагоналям четырехугольника ABCD значит BDAC. тверждение 3. Если отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, перпендикулярны, то диагонали четырехугольника равны.
тверждение 3. Если отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, перпендикулярны, то диагонали четырехугольника равны.









