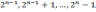Внеурочное занятие.
Тема: Парадоксы теории множеств.
Учащиеся 7- 8 классов.
Учителя: Аннухина О. В., Киселева Т.А.
Цель:
-знакомство учащихся с понятием парадокса теории множеств.
Задачи:
- развивать умение ориентироваться на разнообразие способов решения задач;
- учитывать правило в планировании и контроле способа решения;
-формировать умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.
-формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Технологическая карта занятия.
| № | Этап занятия | Деятельность учителя
| Деятельность ученика | Формируемые УУД |
| Познавательные | Регулятивные | Коммуникативные | Личностные |
| 1 | 2 | 5 | 6 | 8 | 9 | 10 | 11 |
| 1 | Организационно-мотивационный | Приветствие учащихся; проверка учителем готовности детей к занятию, организация внимания; Интрига. | Слушают учителя, настраиваются на работу | Осознанное и произвольное построение речевого высказывания | Прогнозирование своей деятельности | Умение слушать и вступать в диалог | Умение выделять нравственный аспект поведения |
| 2 | Актуализация опорных знаний. | Организация игры – «Составь слово»
| Отвечают на вопросы, которые помогут сформулировать тему и цель занятия. | Поиск способа решения задачи. | Формулирование темы. Постановка цели, учебной задачи. | Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог | Смыслообразование |
| 3 | Работа в группе. | Вместе с учениками определяет цель работы. Выступает в роли консультанта. | Знакомятся с парадоксом брадобрея. Решают задачу. Оформляют решение задачи как мини – проект. | Структурирование знаний. Анализ объектов. | Целеполагание Умение распределять обязанности в группе. Планирование своей деятельности для решения поставленной задачи и контроль полученного результата. | Умение слушать и вступать в диалог. Продуктивно общаться и взаимодействовать с одноклассниками в совместной деятельности. | Ориентация в межличностных отношениях |
| 4 | Защита мини - проекта | Комментирует, направляет работу учащихся. | Представители группы защищают проект. | Выражать смысл ситуации различными средствами. | Регулировать весь процесс выполнения учебной задачи. | С достаточной полнотой и точностью выражать свои мысли в соответствии с задачами. | Формирование навыков сопоставления, сравнения. |
| 5 | Самооценка | Слушает, комментирует учащихся. | Оценивают себя, свою работу в группе, работу других ребят в группе. Записывают результаты самооценки в лист самооценки. |
| Адекватно оценивать свои достижения, осознавать возникающие трудности, искать их причины и пути преодоления. | Развивать умение использовать языковые средства. |
|
Ход занятия.
| Этап занятия | Деятельность учителя | Деятельность учащихся |
| 1.Организационно – мотивационный | Прочитайте высказывание Б. Шоу "Если у двух человек есть по одному яблоку, и они обмениваются ими, у каждого из них окажется по одному яблоку. Но если у двух человек есть по одной идее и они обмениваются ими, у каждого будет по две идеи" (Б. Шоу). Я надеюсь, что сегодня вы проявите активность и последуете совету Б.Шоу - делиться идеями. | Слушают, настраиваются на работу. |
| 2. Актуализация опорных знаний. | Ученикам предлагается ответить на вопросы: 1. Что такое множество? - На самом деле никто толком не знает что такое множество. В математике нет точного определения этого понятия. Рассмотрим слово МНОЖЕСТВО. 3. Как записать множество букв, из которых состоит это слово? 4. Из скольких элементов состоит это множество? 5. Составьте слова из элементов данного множества и запишите полученные слова. (Ученикам выдаются карточки с буквами – 8шт) 6. Почему вы не составили слово «множество»? - Возникла первая проблема: в русском алфавите одна буква О, а в слове МНОЖЕСТВО две. Почему вторую букву О писать не надо, можно объяснить, произнеся такое заклинание: множество определяется своими элементами, т. е. каждый элемент в множестве встречается только один раз. 7. Но что делать, если нам всё-таки нужны две буквы О?( надо как-то различать эти две буквы О, например, назвать их О1 и О2) 8. Как теперь будет выглядеть множество? Запишите его. - Теперь с точки зрения русского языка всё в порядке: букв О две, и мы можем спокойно составлять слова с двумя буквами О. С точки зрения теории множеств тоже всё хорошо: двух одинаковых элементов в одном множестве нет. Итак, эту проблему мы решили. 9. Каким словом можно назвать похожую ситуацию (противоречие, которое возникает в процессе логического мышления)? Задание с опережением: «Найти определение понятия парадокса, парадокса в теории множеств». Сформулируем тему занятия. | Учащиеся отвечают на вопросы учителя. Составляют слова из букв. Выступает ученик с сообщением. Формулируют тему занятия, ставят цели и задачи.
|
| 3. Работа в группе | Каждой группе учащихся предлагается парадокс брадобрея. В одном полку жил-был полковой парикмахер, которого по историческим причинам называют брадобреем. Однажды командир приказал ему брить тех и только тех, кто не бреется сам. Брадобрей, получив приказ, сначала обрадовался, потому что многие солдаты умели бриться сами, побрил тех, кто бриться сам не умел. -А что ему с собой-то делать? (Ведь если он будет брить себя, то нарушит приказ командира не брить тех, кто бреется сам. Брадобрей уже решил было, что брить себя не будет. Но тут его осенила мысль, что если он сам себя брить не будет, то окажется, что он сам не бреется, и по приказу командира он должен всё-таки себя побрить…) Что с ним стало, история умалчивает. Причём же здесь теория множеств? А вот причём: командир пытался определить множество людей, которых брадобрею нужно брить, таким образом: {те и только те, кто не бреется сам}. Казалось бы, обычное множество, описывается несколькими русскими словами, чем оно хуже, например, множества {все ученики школы}? Но с этим множеством тут же возникает проблема: непонятно, принадлежит ли этому множеству брадобрей. Столкнувшись с этими парадоксами, создатели теории множеств осознали, что нельзя задавать множества произвольными словосочетаниями. После этого они стали бороться с парадоксами двумя способами. Первый способ— способ Кантора, придумавшего «наивную теорию множеств», в которой запрещаются все действия и операции, ведущие к парадоксам. Другой способ— аксиоматический. Идея способа Кантора заключается в следующем: разрешается работать со множествами, которые «встречаются в природе». -Приведите примеры таких множеств. Также разрешается работать со множествами, которые получаются из них разумными теоретико-множественными операциями. Какие операции над множествами вы знаете? -Найдите пересечение и объединение предложенных вами множеств.
- Как это можно изобразить графически? Предлагает задачу, которую нужно решить в группах разными способами(7 класс – круги Эйлера, 8 класс формула включения- исключения) Учитель предлагает выбрать руководителя группы, распределить обязанности для успешной работы. Учитель выступает в роли консультанта. | Отвечают на вопросы учителя. Обсуждают проблему: «Бриться или не бриться?» Составляют план работы по решению задачи, решают задачу, оформляют мини-проект. |
| 4. Защита мини-проектов | Слушаем ответы учащихся, исправляем ошибки. | Учащиеся защищают мини-проекты. 7 класс рассказывает решение задачи с помощью кругов Эйлера 8 класс – с помощью формулы. Показывают 7-ми классникам как обозначается количество элементов множества, знакомят с формулой включения – исключения. |
| 5. Самооценка |
| Учащиеся оценивают свою работу в группе, работу группы. Записывают результат оценивания в лист самооценки. От каждой группы выступает по одному учащемуся со своей самооценкой. |
| 6. Рефлексия | Вернёмся к эпиграфу нашего занятия. - Как вы считаете, произошёл у вас сегодня обмен идеями? - Что нового вы узнали на занятии? При развитии теории множеств, на которой базируется вся современная математика, возникали парадоксы. Например, парадокс брадобрея, но существуют другие парадоксы, с которыми мы вам предлагаем познакомиться самостоятельно и оформить в виде проекта по окончанию курса. | Дети отвечают на вопросы учителя.
|
| 7. Домашнее задание | 1) Задача «Дед Мороз и конфеты» 2) Создать проект по теме «Парадоксы теории множеств», работая в группе. |
|
Приложение 1
В одном полку жил-был полковой парикмахер, которого по историческим причинам называют брадобреем. Однажды командир приказал ему брить тех и только тех, кто не бреется сам. Брадобрей, получив приказ, сначала обрадовался, потому что многие солдаты умели бриться сами, побрил тех, кто бриться сам не умел.
-А что ему с собой-то делать?
В одном полку жил-был полковой парикмахер, которого по историческим причинам называют брадобреем. Однажды командир приказал ему брить тех и только тех, кто не бреется сам. Брадобрей, получив приказ, сначала обрадовался, потому что многие солдаты умели бриться сами, побрил тех, кто бриться сам не умел.
-А что ему с собой-то делать?
В одном полку жил-был полковой парикмахер, которого по историческим причинам называют брадобреем. Однажды командир приказал ему брить тех и только тех, кто не бреется сам. Брадобрей, получив приказ, сначала обрадовался, потому что многие солдаты умели бриться сами, побрил тех, кто бриться сам не умел.
-А что ему с собой-то делать?
В одном полку жил-был полковой парикмахер, которого по историческим причинам называют брадобреем. Однажды командир приказал ему брить тех и только тех, кто не бреется сам. Брадобрей, получив приказ, сначала обрадовался, потому что многие солдаты умели бриться сами, побрил тех, кто бриться сам не умел.
-А что ему с собой-то делать?
В одном полку жил-был полковой парикмахер, которого по историческим причинам называют брадобреем. Однажды командир приказал ему брить тех и только тех, кто не бреется сам. Брадобрей, получив приказ, сначала обрадовался, потому что многие солдаты умели бриться сами, побрил тех, кто бриться сам не умел.
-А что ему с собой-то делать?
В одном полку жил-был полковой парикмахер, которого по историческим причинам называют брадобреем. Однажды командир приказал ему брить тех и только тех, кто не бреется сам. Брадобрей, получив приказ, сначала обрадовался, потому что многие солдаты умели бриться сами, побрил тех, кто бриться сам не умел.
-А что ему с собой-то делать?
В одном полку жил-был полковой парикмахер, которого по историческим причинам называют брадобреем. Однажды командир приказал ему брить тех и только тех, кто не бреется сам. Брадобрей, получив приказ, сначала обрадовался, потому что многие солдаты умели бриться сами, побрил тех, кто бриться сам не умел.
-А что ему с собой-то делать?
В одном полку жил-был полковой парикмахер, которого по историческим причинам называют брадобреем. Однажды командир приказал ему брить тех и только тех, кто не бреется сам. Брадобрей, получив приказ, сначала обрадовался, потому что многие солдаты умели бриться сами, побрил тех, кто бриться сам не умел.
-А что ему с собой-то делать?
В одном полку жил-был полковой парикмахер, которого по историческим причинам называют брадобреем. Однажды командир приказал ему брить тех и только тех, кто не бреется сам. Брадобрей, получив приказ, сначала обрадовался, потому что многие солдаты умели бриться сами, побрил тех, кто бриться сам не умел.
-А что ему с собой-то делать?
Приложение 2
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
В классе 25 учащихся, и все они любят математику. Известно, что 23 ученика любят алгебру, а 21 – геометрию. Сколько учащихся этого класса любят и алгебру и геометрию?
Приложение3
ЛИСТ САМООЦЕНКИ
| Вид работы | Самооценка |
| Разминка Игра «Составь слово». | Какие вопросы вызвали затруднения? Твоё эмоциональное состояние. |
|
| Работа в группе по созданию мини-проекта | Твоя роль в группе. Задание выполнено полностью самостоятельно или была оказана помощь? Какие затруднения испытывал? Твоё эмоциональное состояние. Оцени работу всей группы. |
|
| Итоги | Оцени свою работу на протяжении всего занятия. |
|
ЛИСТ САМООЦЕНКИ
| Вид работы | Самооценка |
| Разминка Игра «Составь слово». | Какие вопросы вызвали затруднения? Твоё эмоциональное состояние. |
|
| Работа в группе по созданию мини-проекта | Твоя роль в группе. Задание выполнено полностью самостоятельно или была оказана помощь? Какие затруднения испытывал? Твоё эмоциональное состояние. Оцени работу всей группы. |
|
| Итоги | Оцени свою работу на протяжении всего занятия. |
|
ЛИСТ САМООЦЕНКИ
| Вид работы | Самооценка |
| Разминка Игра «Составь слово». | Какие вопросы вызвали затруднения? Твоё эмоциональное состояние. |
|
| Работа в группе по созданию мини-проекта | Твоя роль в группе. Задание выполнено полностью самостоятельно или была оказана помощь? Какие затруднения испытывал? Твоё эмоциональное состояние. Оцени работу всей группы. |
|
| Итоги | Оцени свою работу на протяжении всего занятия. |
|
Приложение 4
Приложение 5
Дед Мороз и конфеты
На Новый год к детишкам пришёл Дед Мороз с мешком конфет. Конфет в мешке бесконечно много, и они занумерованы натуральными числами. На каждой конфете написан её номер, и для каждого натурального числа есть ровно одна конфета с этим номером. За одну минуту до полночи Дед Мороз подарил конфету №1 детям. Через полминуты он дал детям конфеты №2 и №3, но при этом конфету №1 забрал. Ещё через четверть минуты он дал детям конфеты №4, №5, №6 и №7, но забрал конфеты №2 и №3. И так далее: щедрый Дед Мороз каждый раз даёт вдвое больше конфет, чем на предыдущем шаге, и за 
 мин. до полночи даёт конфеты с номерами
мин. до полночи даёт конфеты с номерами 
 , а забирает конфеты с номерами
, а забирает конфеты с номерами 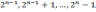
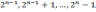 , которые сам же дал на предыдущем шаге. При этом количество конфет у детей стремительно возрастает.
, которые сам же дал на предыдущем шаге. При этом количество конфет у детей стремительно возрастает.
Сколько конфет будет у детей в полночь?
Дед Мороз и конфеты
На Новый год к детишкам пришёл Дед Мороз с мешком конфет. Конфет в мешке бесконечно много, и они занумерованы натуральными числами. На каждой конфете написан её номер, и для каждого натурального числа есть ровно одна конфета с этим номером. За одну минуту до полночи Дед Мороз подарил конфету №1 детям. Через полминуты он дал детям конфеты №2 и №3, но при этом конфету №1 забрал. Ещё через четверть минуты он дал детям конфеты №4, №5, №6 и №7, но забрал конфеты №2 и №3. И так далее: щедрый Дед Мороз каждый раз даёт вдвое больше конфет, чем на предыдущем шаге, и за 
 мин. до полночи даёт конфеты с номерами
мин. до полночи даёт конфеты с номерами 
 , а забирает конфеты с номерами
, а забирает конфеты с номерами 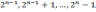
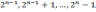 , которые сам же дал на предыдущем шаге. При этом количество конфет у детей стремительно возрастает.
, которые сам же дал на предыдущем шаге. При этом количество конфет у детей стремительно возрастает.
Сколько конфет будет у детей в полночь?
Дед Мороз и конфеты
На Новый год к детишкам пришёл Дед Мороз с мешком конфет. Конфет в мешке бесконечно много, и они занумерованы натуральными числами. На каждой конфете написан её номер, и для каждого натурального числа есть ровно одна конфета с этим номером. За одну минуту до полночи Дед Мороз подарил конфету №1 детям. Через полминуты он дал детям конфеты №2 и №3, но при этом конфету №1 забрал. Ещё через четверть минуты он дал детям конфеты №4, №5, №6 и №7, но забрал конфеты №2 и №3. И так далее: щедрый Дед Мороз каждый раз даёт вдвое больше конфет, чем на предыдущем шаге, и за 
 мин. до полночи даёт конфеты с номерами
мин. до полночи даёт конфеты с номерами 
 , а забирает конфеты с номерами
, а забирает конфеты с номерами 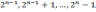
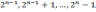 , которые сам же дал на предыдущем шаге. При этом количество конфет у детей стремительно возрастает.
, которые сам же дал на предыдущем шаге. При этом количество конфет у детей стремительно возрастает.
Сколько конфет будет у детей в полночь?