Жизнь и творчество Л. Эйлера. Основные труды и открытия Л. Эйлера.

Жизнь и творчество Л. Эйлера. Основные труды и открытия Л. Эйлера.

Подготовила:

Пихотина Татьяна Викторовна

Леонард Эйлер

День рождения: 15.04.1707 года Возраст: 76 лет Место рождения: Базель, Швейцария. Дата смерти: 18.09.1783 года Место смерти: Санкт-Петербург Гражданство: Швейцария

Выдающийся математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.

Эйлер — автор более чем 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др. Многие его работы оказали значительное влияние на развитие науки.

Леонард Эйлер родился в 1707 году в семье базельского пастора, друга семьи Бернулли. Рано обнаружил математические способности. Начальное обучение получил дома под руководством отца, учившегося некогда математике у Якоба Бернулли. Пастор готовил старшего сына к духовной карьере, однако занимался с ним и математикой — как в качестве развлечения, так и для развития логического мышления. Одновременно с обучением в гимназии мальчик увлечённо занимался математикой под руководством Якоба Бернулли, а в последние гимназические годы посещал университетские лекции младшего брата Якоба, Иоганна Бернулли.

Швейцария (1707—1727)

20 октября 1720 года 13-летний Леонард Эйлер стал студентом факультета искусств Базельского университета. Но любовь к математике направила Леонарда по иному пути. Вскоре способный мальчик обратил на себя внимание профессора Иоганна Бернулли. Он передал одарённому студенту математические статьи для изучения, а по субботам пригласил приходить к нему домой, чтобы совместно разбирать непонятное. В доме своего учителя Эйлер познакомился и подружился с сыновьями Бернулли — Даниилом и Николаем, также увлечённо занимавшимися математикой.

Учёная степень магистр

8 июня 1724 года 17-летний  Леонард Эйлер  произнёс на латыни речь о сравнении философских воззрений Декарта и Ньютона и был удостоен учёной степени магистра.

В последующие два года юный Эйлер написал несколько научных работ. Одна из них, «Диссертация по физике о звуке», получившая благоприятный отзыв, была представлена на конкурс для замещения неожиданно освободившейся в Базельском университете должности профессора физики (1725). Но, несмотря на положительный отзыв, 19-летнего Эйлера сочли слишком юным, чтобы включить в число кандидатов на профессорскую кафедру.

В начале зимы 1726 года Эйлеру сообщили из Санкт-Петербурга: по рекомендации братьев Бернулли он приглашён на должность адъюнкта по физиологии с окладом 200 рублей. Получение аванса для компенсации проездных расходов растянулось почти на год, и лишь 5 апреля 1727 года Эйлер навсегда покинул родную Швейцарию.

А. С. Пушкин приводит романтический рассказ: якобы Эйлер составил гороскоп для новорождённого Иоанна Антоновича (1740), но результат его настолько испугал, что он никому не стал его показывать, и лишь после смерти несчастного царевича рассказал о нём графу К. Г. Разумовскому. Достоверность этого исторического анекдота крайне сомнительна.

Интересные факты

Маркиз Кондорсе сообщает, что вскоре после переезда в Берлин Эйлера пригласили на придворный бал. На вопрос королевы-матери, отчего он так немногословен, Эйлер ответил: «Прошу меня простить, но я только что из страны, где за лишнее слово могут повесить».

Интересные факты

Другой рассказ Кондорсе: однажды два студента, выполняя независимо сложные астрономические вычисления, получили немного различающиеся результаты в 50-м знаке, и обратились к Эйлеру за помощью. Эйлер проделал те же вычисления в уме и указал правильный результат.

Интересные факты

Рассказывают, что Эйлер не любил театра, и если попадал туда, поддавшись уговорам жены, то чтобы не скучать, выполнял в уме сложные вычисления, подобрав их объём так, чтобы хватило как раз до конца представления.

В 1739 году вышла работа Эйлера «Tentamen novae theoriae musicae» по математической теории музыки. По поводу этой работы ходила шутка, что в ней слишком много музыки для математиков и слишком много математики для музыкантов.

Если до него достижения в области математики были разрозненны и не всегда согласованны, то Эйлер впервые увязал анализ, алгебру, тригонометрию, теорию чисел и др. дисциплины в единую систему, и добавил немало собственных открытий. Значительная часть математики преподаётся с тех пор «по Эйлеру».

Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплексную экспоненту с тригонометрическими функциями.

Формула Эйлера утверждает, что для любого вещественного числа x выполнено следующее равенство:

Где e — основание натурального логарифма,

i — мнимая единица.

Формула Эйлера

Сравнение по модулю натурального числа n — в теории чисел отношение эквивалентности на кольце целых чисел, связанное с делимостью на n. Факторкольцо по этому отношению называется кольцом вычетов. Совокупность соответствующих тождеств и алгоритмов образует модульную (или модулярную) арифметику.

Сравнение по модулю

Цепная дробь (или непрерывная дробь) — это математическое выражение вида

где a0 есть целое число и все остальные an натуральные числа (положительные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или бесконечной). Число представляется конечной цепной дробью тогда и только тогда, когда оно рационально. Число представляется периодической цепной дробью тогда и только тогда, когда оно является квадратичной иррациональностью.

Непрерывная дробь

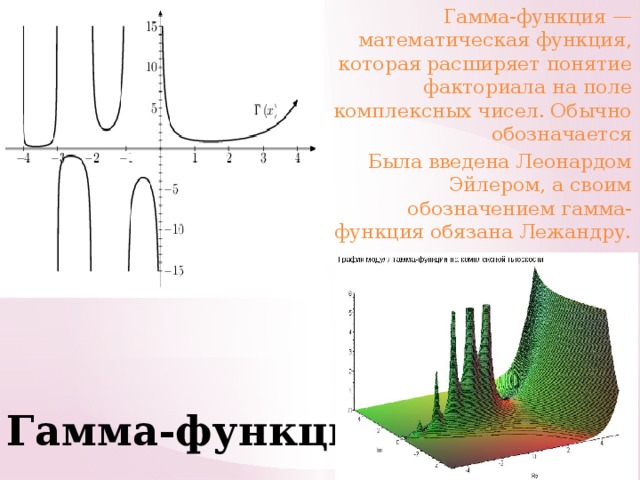
Гамма-функция — математическая функция, которая расширяет понятие факториала на поле комплексных чисел. Обычно обозначается

Была введена Леонардом Эйлером, а своим обозначением гамма-функция обязана Лежандру.

Гамма-функция

Эйлер создал несколько новых математических дисциплин — теорию чисел, вариационное исчисление, теорию комплексных функций, дифференциальную геометрию поверхностей, специальные функции.

Теория чисел, или высшая арифметика — раздел математики, изучающий целые числа и сходные объекты. В теории чисел в широком смысле рассматриваются как алгебраические, так и трансцендентные числа, а также функции различного происхождения, которые связаны с арифметикой целых чисел и их обобщений.

Вариацио́нное исчисле́ние — это раздел функционального анализа, в котором изучаются вариации функционалов. Самая типичная задача вариационного исчисления состоит в том, чтобы найти функцию, на которой заданный функционал достигает экстремального значения.

Специальные функции — встречающиеся в различных приложениях математики (чаще всего — в различных задачах математической физики) функции, которые не выражаются через элементарные функции. Специальные функции представляются в виде рядов или интегралов.

Математические дисциплины

Эйлер много внимания уделял представлению натуральных чисел в виде сумм специального вида и сформулировал ряд теорем для вычисления числа разбиений.

Он исследовал алгоритмы построения магических квадратов методом обхода шахматным конём.

При решении комбинаторных задач он глубоко изучил свойства сочетаний и перестановок, ввёл в рассмотрение числа Эйлера .

Комбинаторика

Магический квадрат Эйлера

Углы Эйлера

Геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.  

Круги Эйлера

Список источников