В основі вивчення будь-якої теми є не лише навчити, сформування вміння у розв’язуванні задач, але і показати використання вивченого. Учням важко працювати з прикладними задачами, тому що вони звикли бачити математичну модель – абстрактну і „зацифровану”. Здебільшого ми вчимо математику задля самої ж математики. Давайте подивимось ширше. Я пропоную переглянути урок з теми „Знаходження найбільшого та найменшого значення функції на проміжку”.
Мета: узагальнити поняття найбільшого і найменшого значення функції, ввести поняття найбільшого і найменшого значення функції на проміжку, скласти алгоритм розв’язування типових задач, показати застосування на конкретних прикладних задачах.
Чи не задумувались ви, чому людину цікавлять крайнощі, чому розумна істота не може задовольнитись золотою серединою. На мою думку, до цього спонукає інтерес, жадоба пізнання. Саме вивчення екстремальних, критичних ситуацій призводить спочатку до гіпотези, а пізніше – до наукового факту.
Всьому свій час, всьому жорстока міра.
Спіраль життя до дивного проста.
У всякій вірі є своя зневіра,
А із невіри – віра пророста.
У математиці, фізиці, техніці, а також у повсякденному житті часто виникає питання про знаходження найбільшого та найменшого значення деякої величини при невизначених умовах, які ця величина повинна задовольняти.
Задача 1. Знайти найбільше і найменше значення функції.
Y = A sin X + Вcos X
Задачі такого типу розглядаються у програмі 10 класу.
Тому повторимо.
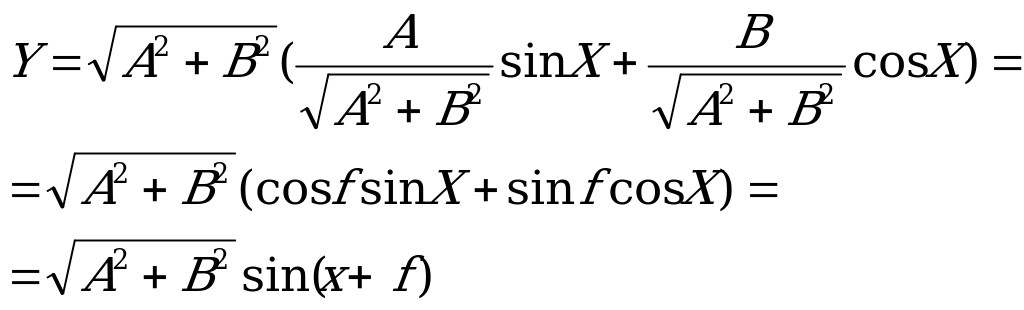
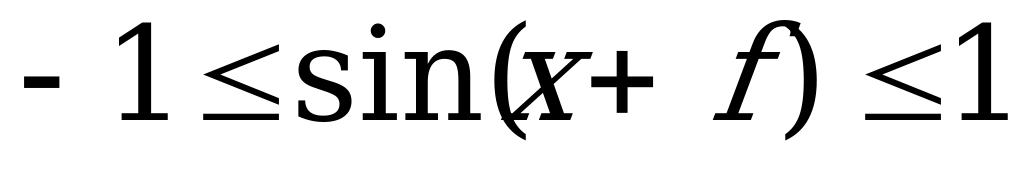
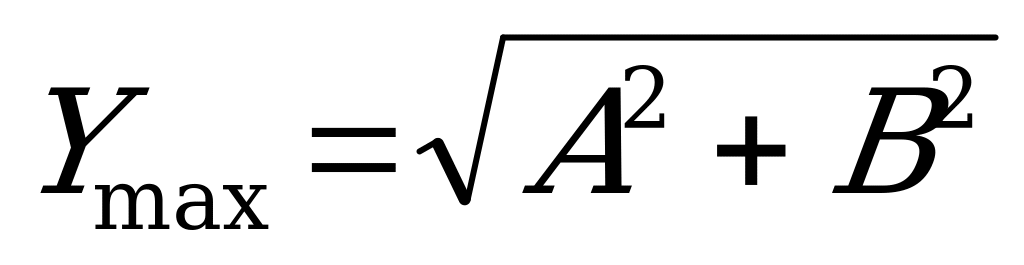
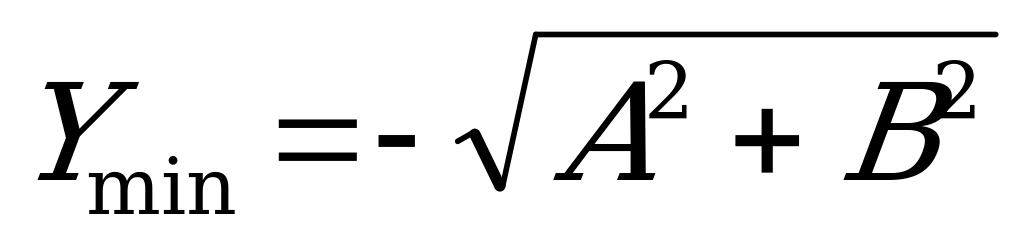
Задача 2. Потрібно сконструювати вікно заданої форми так, щоб воно пропускало найбільше світла. Периметр вікна 2 м.

Наше завдання, сконструювати вікно найбільшої площі. Дослідимо спочатку елементарними засобами:

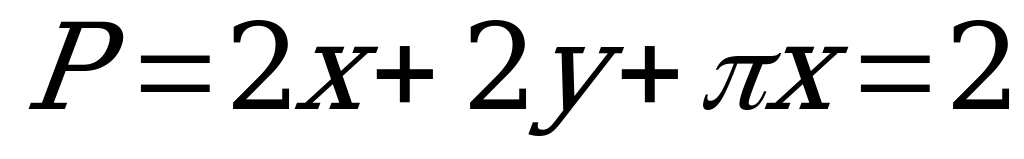
2y 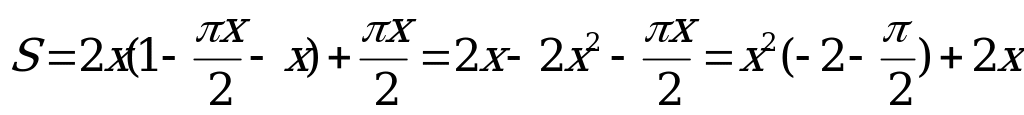
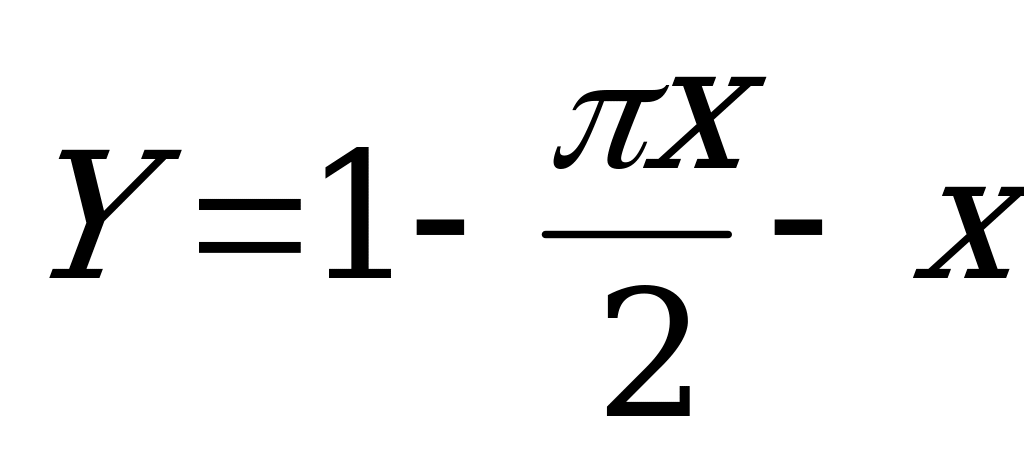
2x
Геометричний зміст: графік – парабола з вітками направленими вниз, тому
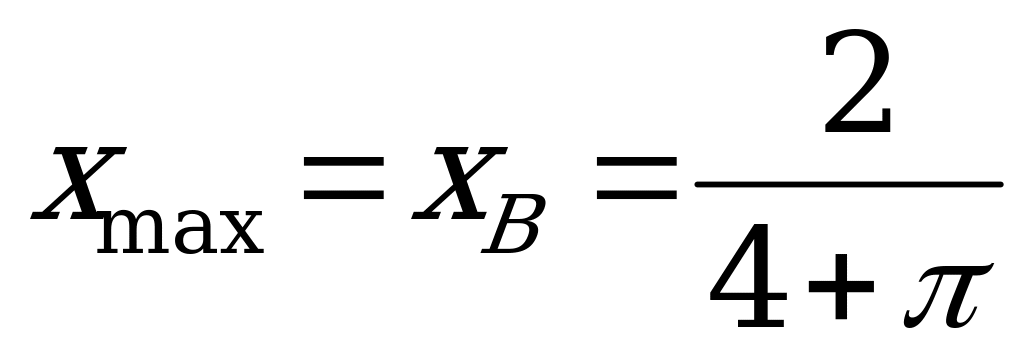
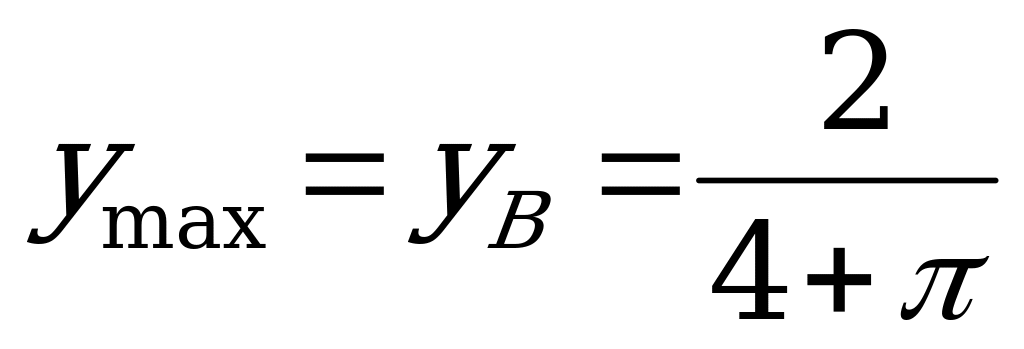
Алгебраїчний зміст: виділити квадрат двочлена.
У курсі математичного аналізу доводиться теорема Вейєрштрасса, яка стверджує, що неперервна на проміжку (а, в) функція приймає на цьому проміжку найбільше і найменше значення. Теорема дає лише впевненість в існуванні найбільших та найменших значень, але не вказує, як знаходити ці значення. Для випадку, коли функція не лише неперервна, але й має обмежене число критичних точок, вкажемо правило знаходження найбільшого та найменшого значень. Нехай спершу, функція на проміжку не має критичних точок. Тоді на цьому проміжку вона є монотонною, тобто зростає або спадає, а, отже, найбільше і найменше значення приймає на кінцях. Якщо функція має обмежене число критичних точок, то найбільше і найменше значення вона приймає у цих точках.
Висновок: щоб знайти найбільше і найменше значення потрібно знайти значення функції на кінцях проміжка і у критичних точках. З отриманих чисел вибрати найбільше і найменше. Але використати це правило можна лише за наявності наступних умов:
Функція повинна бути неперервною.
Число критичних точок на проміжку повинно бути обмеженим.
Повернімось до задачі 2.
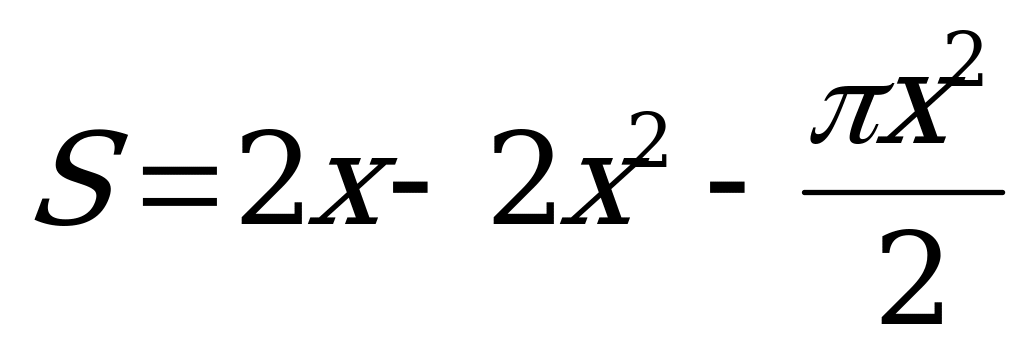
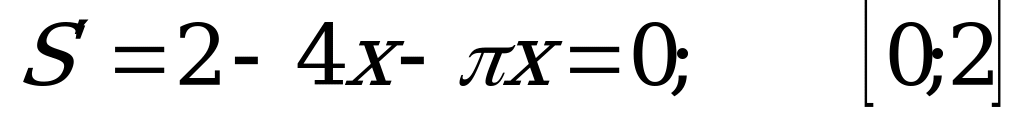
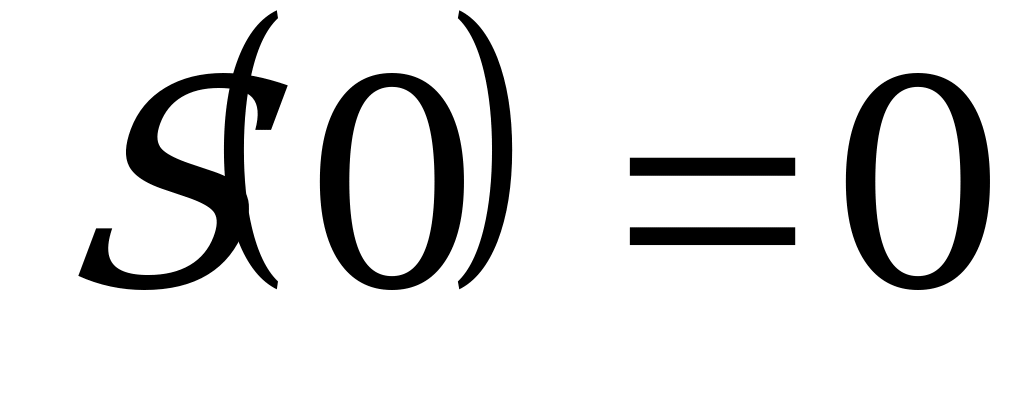
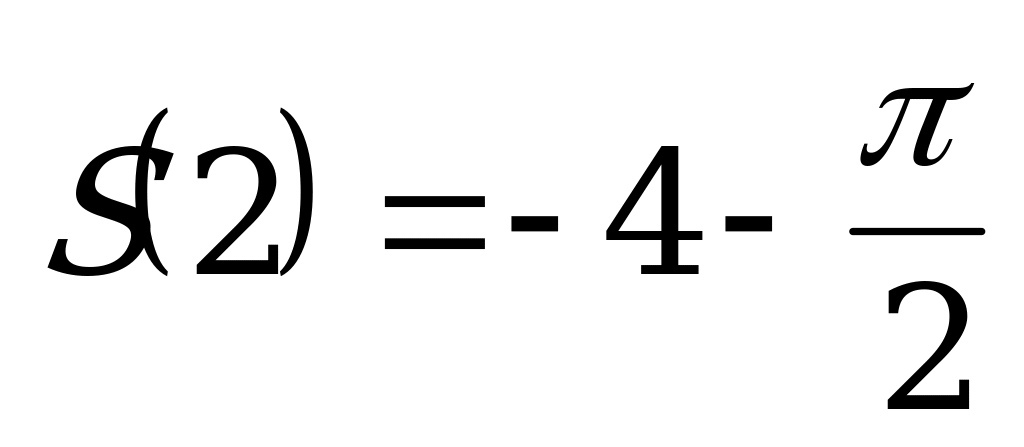
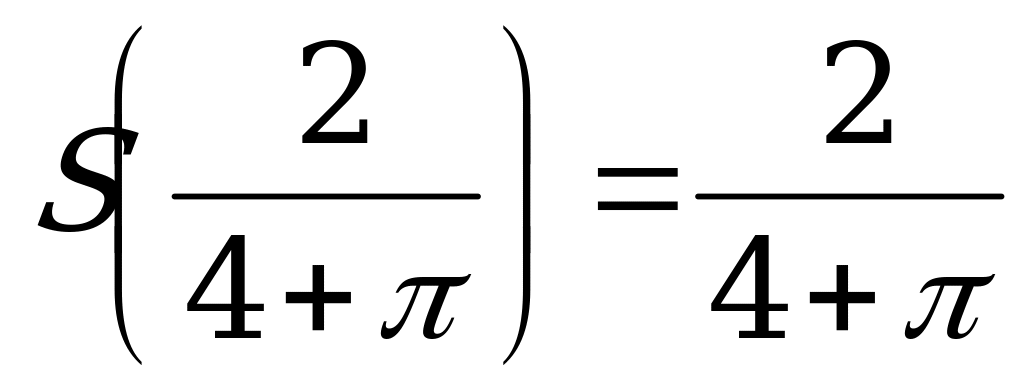
Спробуйте зробити висновок щодо розмірів вікна самостійно.
Складемо алгоритм розв’язування задач.
Довільно обирають незалежну змінну і через неї виражають іншу, для якої будемо шукати найбільше і найменше значення.
Знаходять проміжок зміни незалежної змінної.
Знаходять похідну та шукають її нулі.
Обчислюють значення функції на кінцях проміжка та в критичних точках.
В основі лежить утворення залежності, тобто функції. Вперше цей термін прозвучав у роботах Лейбниця, Ейлер дещо вдосконалив це поняття і вже у 1822 році французький математик Фур’є у своїх працях використовував саме широке поняття функції з тими елементами, які ми використовуємо зараз.
Задачі 3 і 4 учні розв’язують з коментуванням біля дошки.
Задача 3. Знайти число, яке у сумі зі своїм квадратом, дає цій сумі найменше значення.
Задача 4. Як зігнути кусок дроту довжиною L, щоб площа обмеженого ним прямокутника, була найбільшою?
Задача 5. Знайти найбільше і найменше значення функції на проміжку.
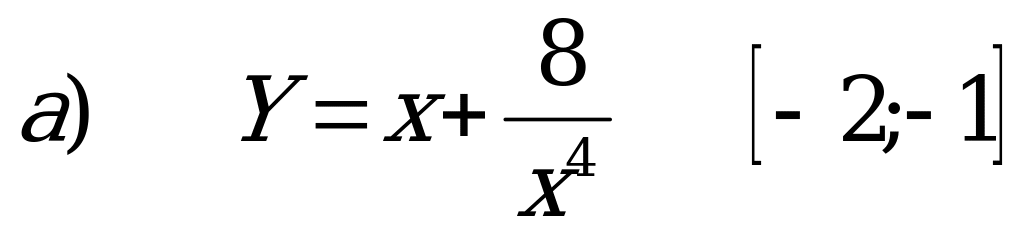
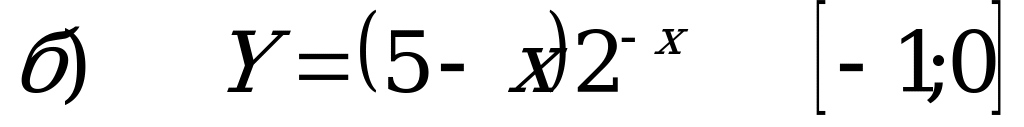
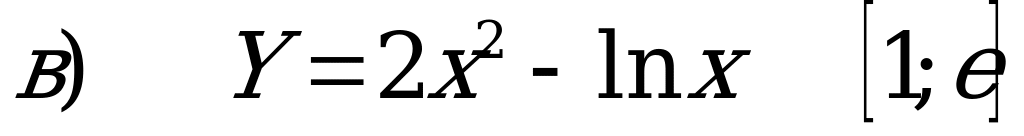
Дане завдання можна розв'язати по варіантах.
Хочу звернути особливу увагу на наступні задачі, оскільки вони виходять за межі самої лише математики.
Задача 6. Вартість плавання судна за 1 год. визначається за формулою a+bv3, a і в – константи, v – швидкість човна (перший доданок пов’язаний з витратами на амортизацію та утримання команди, а другий – з витратами пального). При якій швидкості судно пройде шлях L з найменшими витратами?
Розв’язання:
S = (a+bv3)t – вартість плавання судна в t годин.
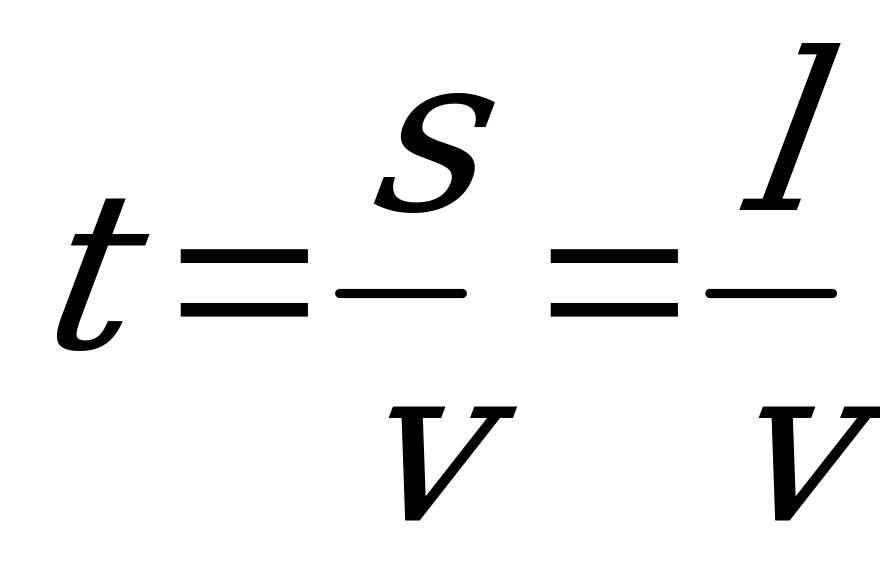
витрати: 
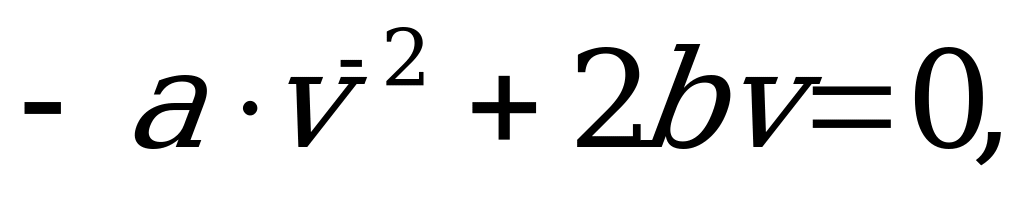
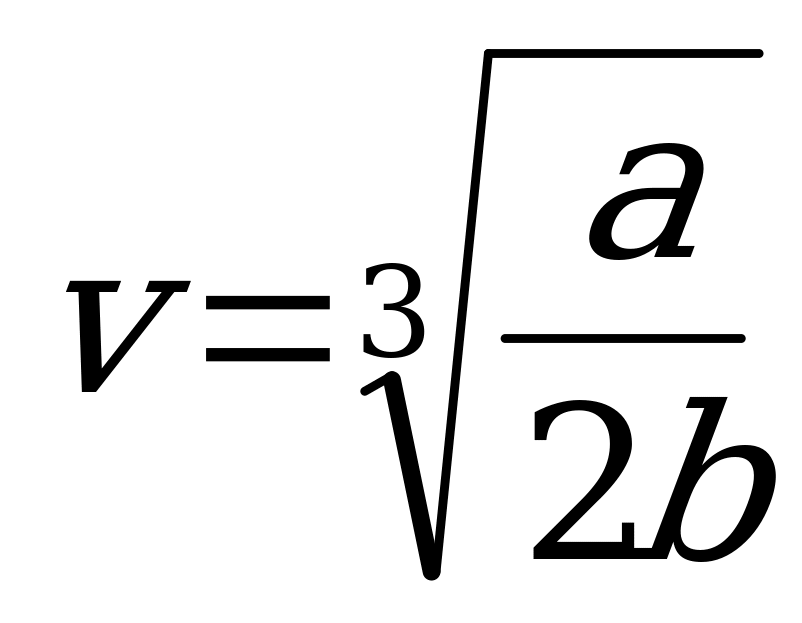
Задача 7. Границя міцності для мостів стальних конструкцій є величина змінна. При 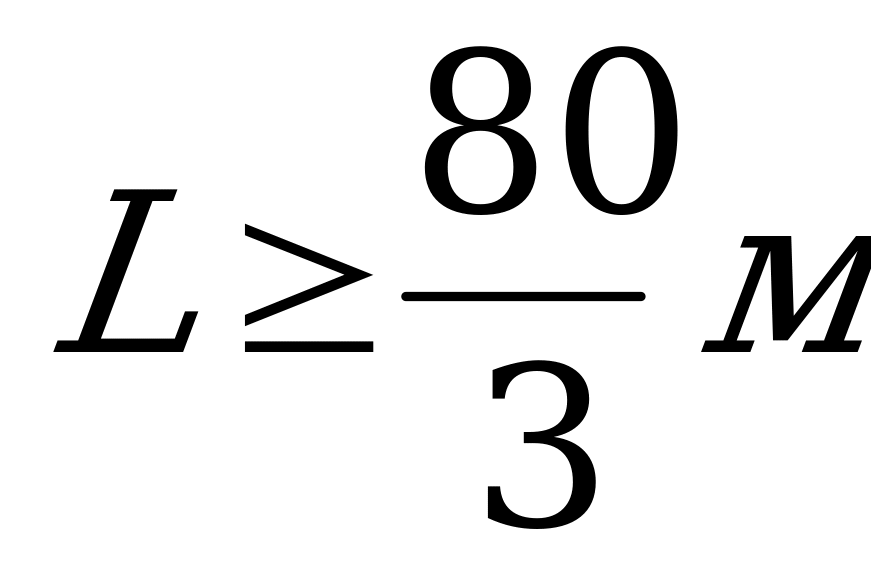 рівняння прогину має вигляд:
рівняння прогину має вигляд:
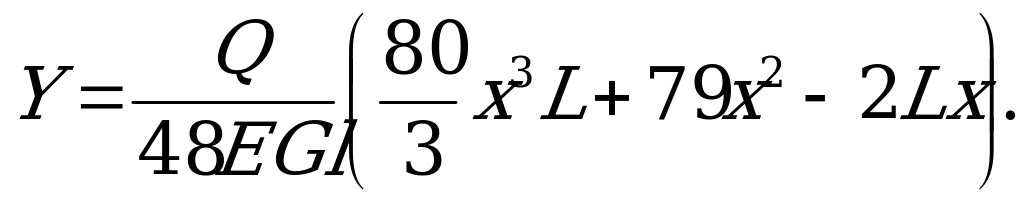
Знайти найбільший (максимально допустимий) прогин конструкції, після якого настає руйнація.
Розв’язання:
нехай Х- прогин конструкції.
Знайдемо похідну
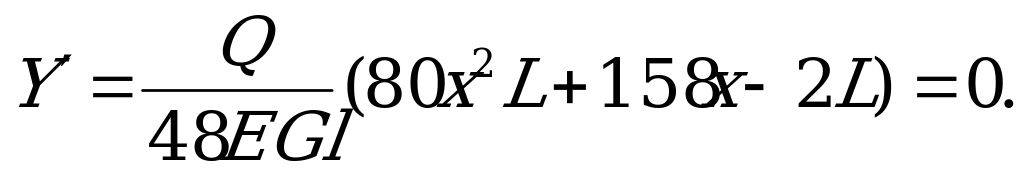
Розв’язуючи квадратне рівняння 80х2L+158x-2L=0
отримаємо D=b2-4ac=24964+640L2
x=-158+(24964+640L2)0,5
-------------------------- = 0,128
2*80*30
x=-158-(24964+640L2)0,5
---------------------------,
2*80*30
не має змісту, оскільки
Відповідь: найбільший прогин конструкції є величина змінна, що залежить від L: x=-158+(24964+640L2)0,5
Задача 8. Водний канал повинен мати задану глибину і площу поперечного перерізу. Якщо поперечний переріз є рівнобічна трапеція, то яким повинен бути кут нахилу бічних сторін, щоб при русі води по каналу затрати на опір тертя були мінімальними (тобто, щоб сума нижньої основи і бічних сторін була найменшою).
Розв’язання:
K
B
 C
C
H
A D
Позначимо гострий кут трапеції  .
.
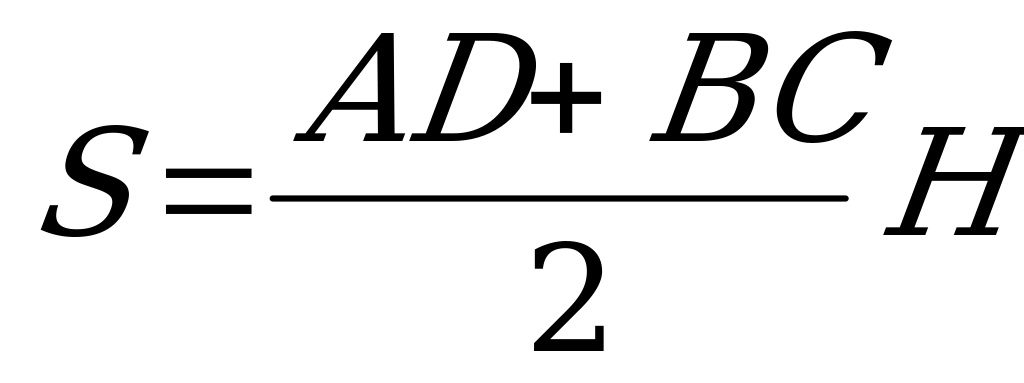
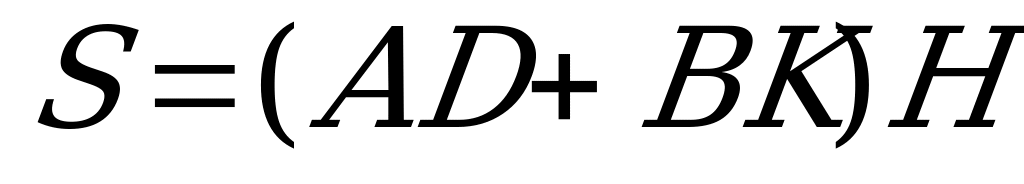

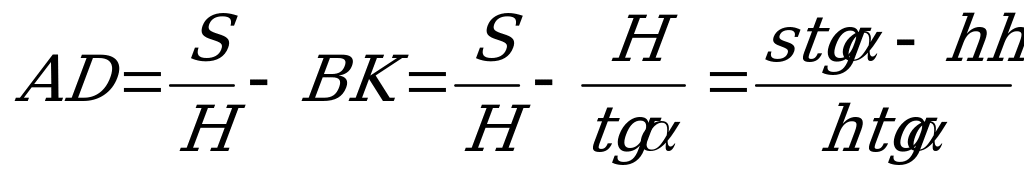
Складемо функцію: F=AB+AD+DC,
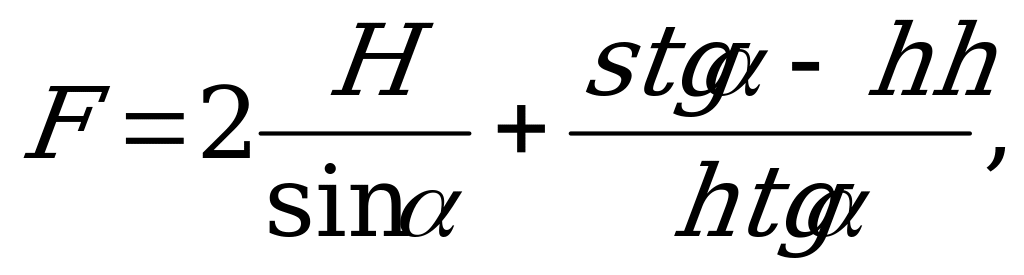
Щоб знайти мінімум функції, візьмемо похідну та прирівняємо до нуля:
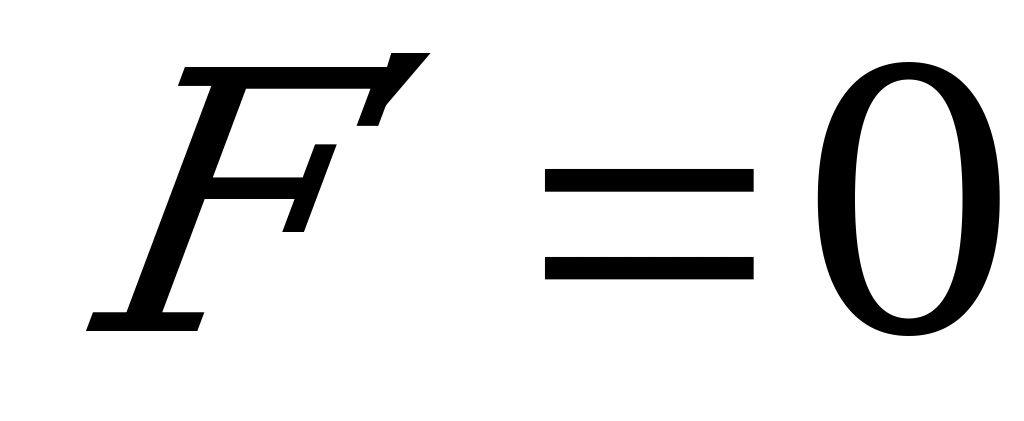
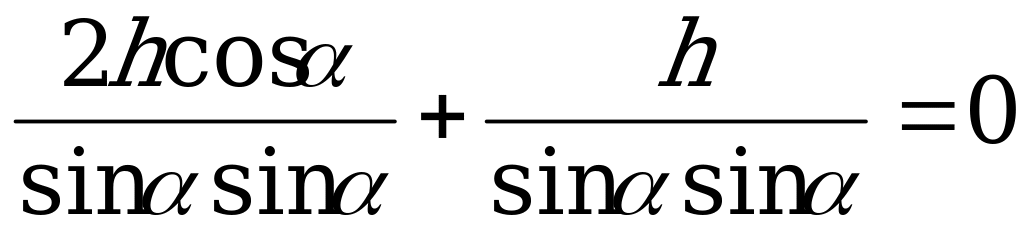
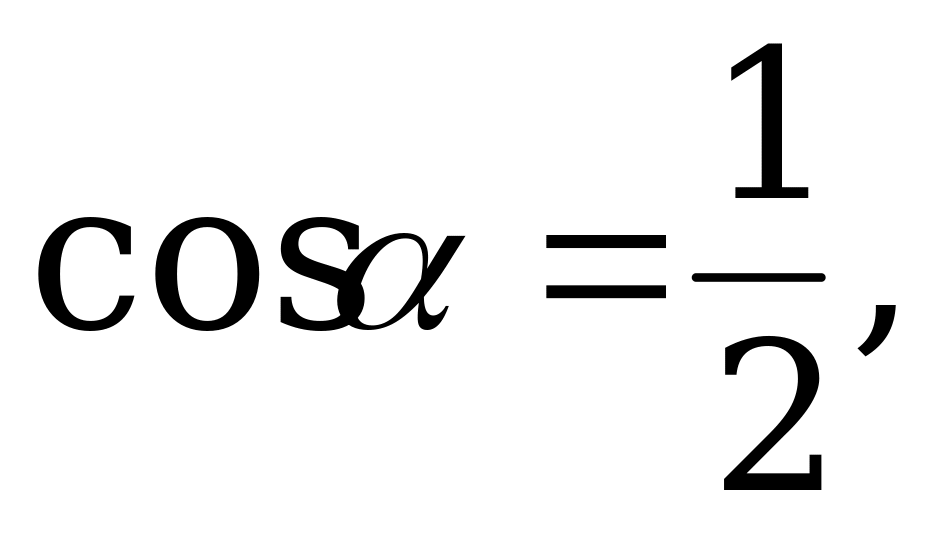
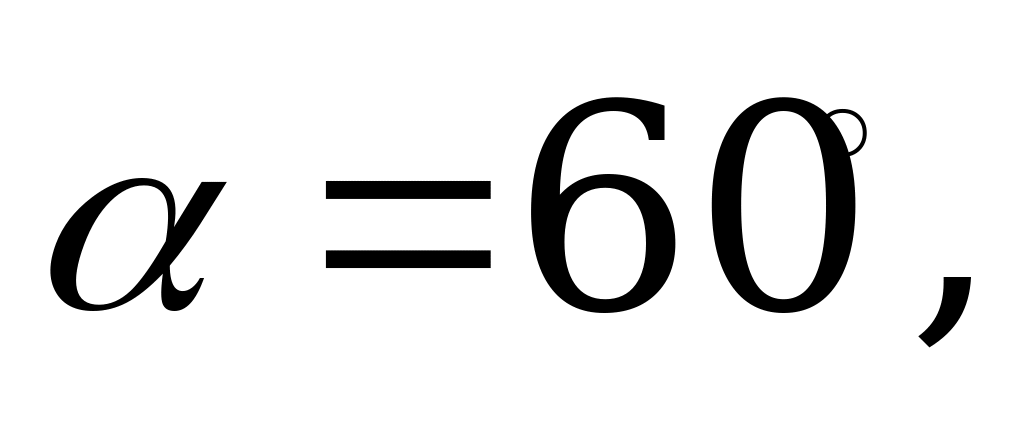
Висновок до задачі учні можуть зробити самостійно.
Домашнє завдання:
У прямокутний трикутник з гіпотенузою 24см і кутом 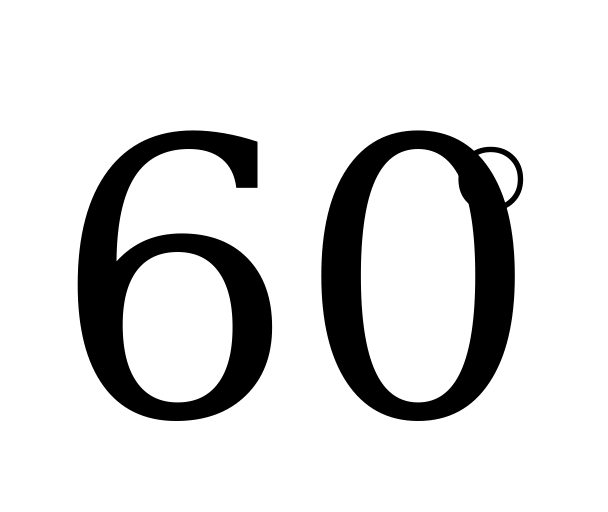 вписати прямокутник, основа якого міститься на гіпотенузі. Якими мають бути сторони прямокутника, щоб його площа була найбільшою.
вписати прямокутник, основа якого міститься на гіпотенузі. Якими мають бути сторони прямокутника, щоб його площа була найбільшою.
В яке коло можна вписати прямокутник найбільшої площі з периметром 56 см.
І ще раз переконуємось в тому, що математика – це млин, який переробляє кількісні співвідношення, які містяться в моделях. І їй все одно де ці співвідношення виникли: в архітектурі, будівництві.
Мука в результаті різна, але це вже справа замовника: що він збирається з неї випікати. Математика свою справу виконала –створила модель, провела розрахунки та інтегрувала до реального життя.
Задача 1. Знайти найбільше і найменше значення функції.
Y = A sin X + Вcos X
Задача 2. Потрібно сконструювати вікно заданої форми так, щоб воно пропускало найбільше світла. Периметр вікна 2 м.

Задача 3. Інд. робота Знайти число, яке у сумі зі своїм квадратом, дає цій сумі найменше значення.
Задача 4. Інд. робота. Як зігнути кусок дроту довжиною L, щоб площа обмеженого ним прямокутника, була найбільшою?
Задача 5. Знайти найбільше і найменше значення функції на проміжку.
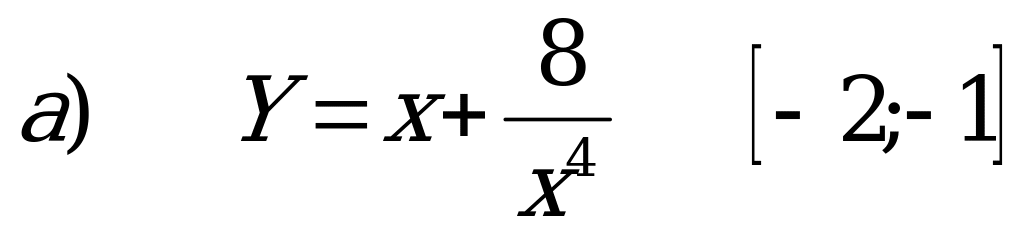 Інд. робота
Інд. робота
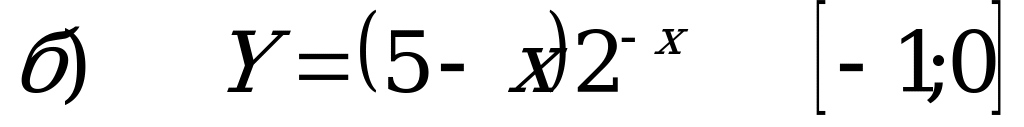 Домашнє завдання
Домашнє завдання
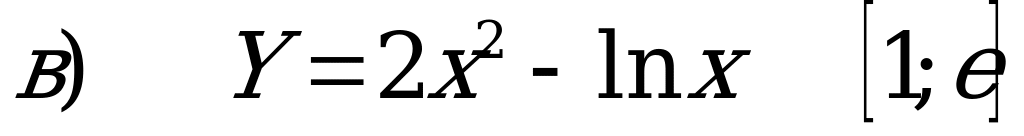 Домашнє завдання
Домашнє завдання
Задача 6. Вартість плавання судна за 1 год. визначається за формулою a+bv3, a і в – константи, v – швидкість човна (перший доданок пов’язаний з витратами на амортизацію та утримання команди, а другий – з витратами пального). При якій швидкості судно пройде шлях L з найменшими витратами?
Задача 7. Границя міцності для мостів стальних конструкцій є величина змінна. При 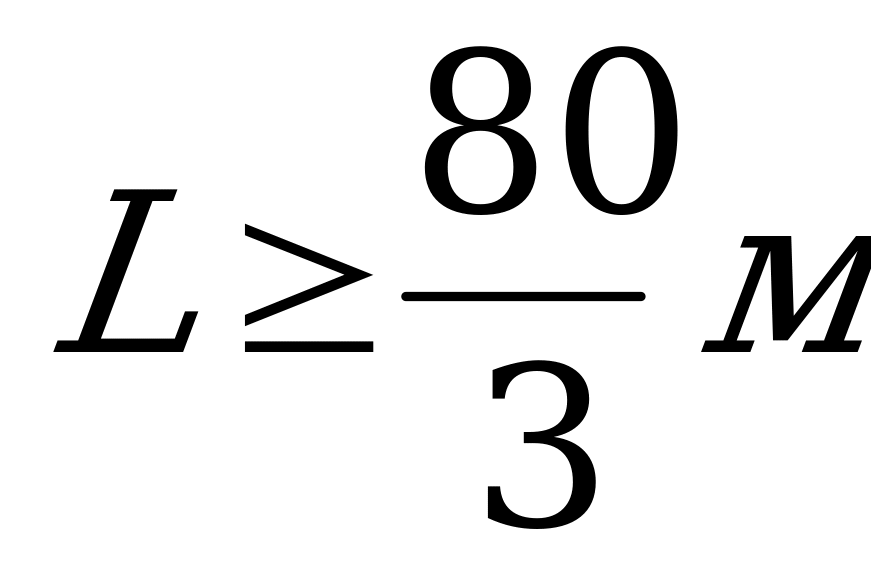 рівняння прогину має вигляд:
рівняння прогину має вигляд:
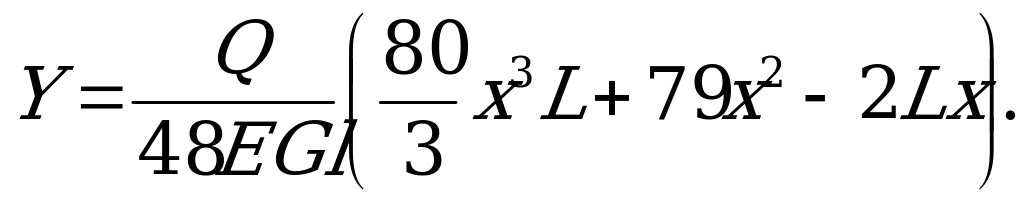
Знайти найбільший (максимально допустимий) прогин конструкції, після якого настає руйнація.
Задача 8. Водний канал повинен мати задану глибину і площу поперечного перерізу. Якщо поперечний переріз є рівнобічна трапеція, то яким повинен бути кут нахилу бічних сторін, щоб при русі води по каналу затрати на опір тертя були мінімальними (тобто, щоб сума нижньої основи і бічних сторін була найменшою).
Щоб знайти найбільше і найменше значення потрібно знайти значення функції на кінцях проміжка і у критичних точках. З отриманих чисел вибрати найбільше і найменше. Але використати це правило можна лише за наявності наступних умов:
Функція повинна бути неперервною.
Число критичних точок на проміжку повинно бути обмеженим.
Алгоритм розв’язування задач.
Довільно обирають незалежну змінну і через неї виражають іншу, для якої шукають найбільше і найменше значення.
Знаходять проміжок зміни незалежної змінної.
Знаходять похідну та шукають її нулі.
Обчислюють значення функції на кінцях проміжка та в критичних точках.
Задача 5. Знайти найбільше і найменше значення функції на проміжку.
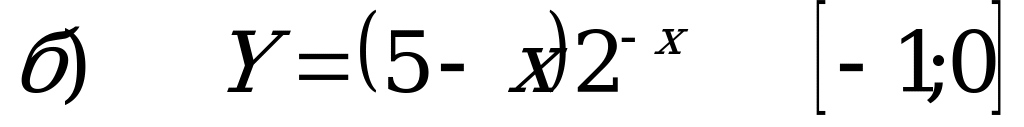 Домашнє завдання
Домашнє завдання
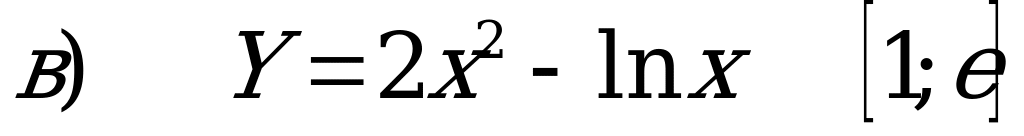 Домашнє завдання
Домашнє завдання
-------------------------------------------------------------------------------------------------------------------------------------------------------
Щоб знайти найбільше і найменше значення потрібно знайти значення функції на кінцях проміжка і у критичних точках. З отриманих чисел вибрати найбільше і найменше. Але використати це правило можна лише за наявності наступних умов:
Функція повинна бути неперервною.
Число критичних точок на проміжку повинно бути обмеженим.
Алгоритм розв’язування задач.
Довільно обирають незалежну змінну і через неї виражають іншу, для якої шукають найбільше і найменше значення.
Знаходять проміжок зміни незалежної змінної.
Знаходять похідну та шукають її нулі.
Обчислюють значення функції на кінцях проміжка та в критичних точках.
Задача 5. Знайти найбільше і найменше значення функції на проміжку.
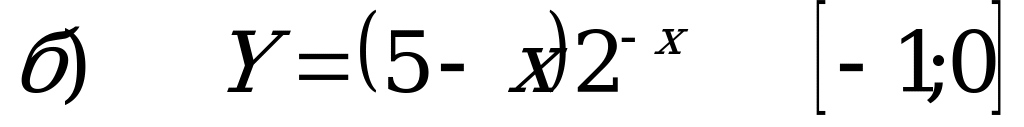 Домашнє завдання
Домашнє завдання
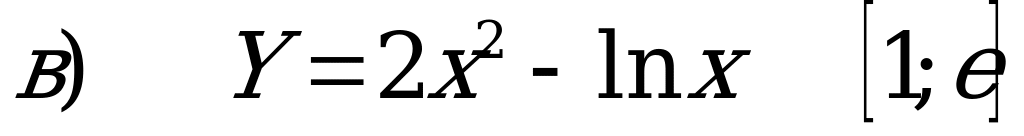 Домашнє завдання.
Домашнє завдання.





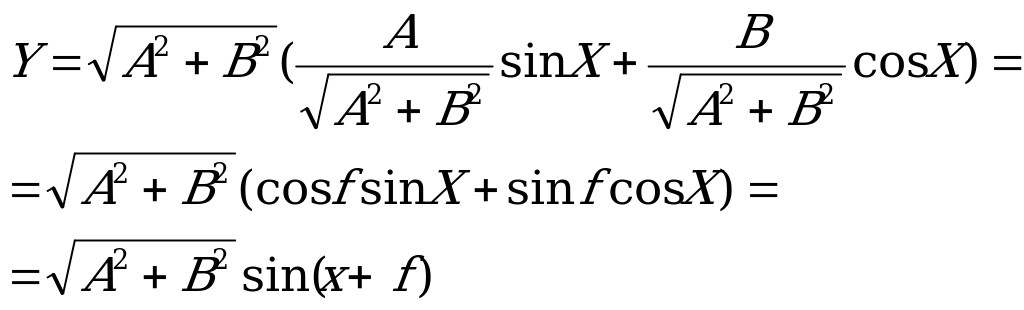


 C
C









