Звездный час четырехугольников

Звездный час

четырехугольников

1 тур

Ребусы

100

Верно- неверно

100

200

Переводчик

Угадай меня

300

200

100

300

100

Обожаю задачи

200

400

300

400

200

100

300

400

200

400

300

400

ДАЛЕЕ

100

100

Ответ: площадь

НАЗАД

200

НАЗАД

200

Ответ: Середина

НАЗАД

Переход хода

300

300

Ответ: диагонали

НАЗАД

400

400

Ответ: трапеция

НАЗАД

100

Периметр параллелограмма равен 28 см,

одна из сторон равна 9 см.

Определите стороны параллелограмма

100

Периметр параллелограмма равен 28 см,

одна из сторон равна 9 см.

Определите стороны параллелограмма

Ответ: 5 см и 9 см

НАЗАД

200

В прямоугольной трапеции разность углов

при одной из боко­ вых сторон равна 48°.

Найдите углы трапеции .

200

В прямоугольной трапеции разность углов

при одной из боко­ вых сторон равна 48°.

Найдите углы трапеции .

Ответ: 90, 90,114,66

НАЗАД

Переход хода

300

В параллелограмме АВСD проведена

биссектриса угла D , которая пересекает

сторону ВС в т Е. ВЕ=2см , СD=8 см.

Найдите периметр параллелограмма АВСD

300

В параллелограмме АВСD проведена

биссектриса угла D , которая пересекает

сторону ВС в т Е. ВЕ=2см , СD=8 см.

Найдите периметр параллелограмма АВСD

Ответ: 36 см

НАЗАД

400

Углы, образуемые диагоналями ромба

с одной из его сторон относятся как 4:5.

Найдите углы ромба

400

Углы, образуемые диагоналями ромба

с одной из его сторон относятся как 4:5.

Найдите углы ромба

Ответ: 80 0 и100 0

НАЗАД

100

• Противоположные стороны и углы

равны.

2) Диагонали пересекаются и точкой пересечения

делятся пополам.

100

• Противоположные стороны и углы

равны.

2) Диагонали пересекаются и точкой пересечения

делятся пополам.

Ответ: параллелограмм

НАЗАД

200

• Сумма углов, прилегающих к одной стороне равна 180º.

2) Диагонали пересекаются и точкой

пересечения делятся пополам

3) Диагонали равны.

4) Диагонали не являются биссектрисами углов.

5) Все углы равны.

200

1) Сумма углов, прилегающих к одной стороне равна 180º.

2) Диагонали пересекаются и точкой пересечения делятся пополам

3) Диагонали равны.

4) Диагонали не являются биссектрисами углов.

5) Все углы равны.

Ответ: прямоугольник

НАЗАД

300

• Сумма углов равна 360º.

2) Все стороны равны.

3)Диагонали точкой пересечения делятся

пополам.

4)Диагонали взаимно перпендикулярны.

5) Диагонали равны.

300

1) Сумма углов равна 360º.

2) Все стороны равны.

3)Диагонали точкой пересечения делятся

пополам.

4)Диагонали взаимно перпендикулярны

5) Диагонали равны

Ответ: квадрат

НАЗАД

400

1)Не всегда сумма углов, прилегающих

к одной стороне равна 180º 2)Только две противоположные стороны

параллельны.

3) Диагонали равны.

400

• Только две противоположные стороны

параллельны

2) Диагонали равны

3) Не всегда сумма углов, прилегающих к одной стороне равна 180º.

Ответ: равнобедренная трапеция

НАЗАД

100

1)Диа­го­наль тра­пе­ции делит её на два рав­ных тре­уголь­ни­ка.

2) Если в ромбе один из углов равен 90° ,

то такой ромб — квад­рат.

100

1)Диа­го­наль тра­пе­ции делит её на два рав­ных тре­уголь­ни­ка.

2) Если в ромбе один из углов равен 90° ,

то такой ромб — квад­рат.

Ответ: 2

НАЗАД

Переход хода

200

• Если один из углов параллелограмма равен 60°,то противоположный ему угол равен 120°.

2) Диагонали квадрата делят его углы пополам.

3) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.

200

• Если один из углов параллелограмма равен 60°,то противоположный ему угол равен 120°.

2) Диагонали квадрата делят его углы пополам.

3) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.

Ответ: 2

НАЗАД

300

• Диа­го­наль па­рал­ле­ло­грам­ма делит его углы

пополам.

2) Если в па­рал­ле­ло­грам­ме диагонали равны, то этот параллелограмм — прямоугольник.

3) Если диа­го­на­ли параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

4) Если один из углов, при­ле­жа­щих к сто­ро­не параллелограмма, равен 50°, то дру­гой угол, при­ле­жа­щий к той же стороне, равен 50°.

300

• Диа­го­наль па­рал­ле­ло­грам­ма делит его углы

пополам.

2) Если в па­рал­ле­ло­грам­ме диагонали равны, то этот параллелограмм — прямоугольник.

3) Если диа­го­на­ли параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

4) Если один из углов, при­ле­жа­щих к сто­ро­не параллелограмма, равен 50°, то дру­гой угол, при­ле­жа­щий к той же стороне, равен 50°.

Ответ: 2,3

НАЗАД

Переход хода

400

• У любой тра­пе­ции бо­ко­вые сто­ро­ны равны.

• Су­ще­ству­ет квадрат, ко­то­рый не яв­ля­ет­ся прямоугольником

• Все углы ромба равны

• В любом пря­мо­уголь­ни­ке диагонали вза­им­но перпендикулярны

• Диагонали равнобедренной трапеции равны

400

• У любой тра­пе­ции бо­ко­вые сто­ро­ны равны.
• Су­ще­ству­ет квадрат, ко­то­рый не яв­ля­ет­ся прямоугольником
• Все углы ромба равны
• В любом пря­мо­уголь­ни­ке диагонали вза­им­но перпендикулярны
• Диагонали равнобедренной трапеции равны

Ответ: 5

НАЗАД

100

Переведите с древнегреческого

« тетрагон»

100

Переведите с древнегреческого

« тетрагон»

Ответ : четырехугольник

НАЗАД

Переход хода

200

В переводе с древнегреческого название этой геометрической фигуры означает «столик».

200

В переводе с древнегреческого название этой геометрической фигуры означает «столик».

Ответ : трапеция

НАЗАД

300

В переводе с древнегреческого

название этой геометрической фигуры означает « бубен ».

300

В переводе с древнегреческого

название этой геометрической фигуры означает « бубен ».

Ответ: ромб

НАЗАД

400

Слово, которым обозначается это понятие, в переводе с греческого означает «натянутая тетива»

400

Слово, которым обозначается это понятие, в переводе с греческого означает «натянутая тетива»

Ответ: гипотенуза .

НАЗАД

2 тур

Без них никуда

Модная штучка

100

100

Всякая всячина

200

Впереди экзамен

100

300

200

300

100

200

400

Площадь, но не

400

100

300

200

Красная

300

400

200

300

400

400

ДАЛЕЕ

100

Сторона квад­ра­та равна 10.

Най­ди­те его площадь.

100

Сторона квад­ра­та равна 10.

Най­ди­те его площадь.

Ответ: 100

НАЗАД

Переход хода

200

Периметр квад­ра­та равен 40 см.

Най­ди­те площадь квадрата.

200

Периметр квад­ра­та равен 40 см.

Най­ди­те площадь квадрата.

Ответ: 100см 2

НАЗАД

300

Найдите сторону квадрата,

площадь которого равна площади прямоугольника со смежными

сторонами 8 м и 18 м

300

Найдите сторону квадрата,

площадь которого равна площади прямоугольника со смежными

сторонами 8 м и 18 м

Ответ: 12 м

НАЗАД

Переход хода

400

Най­ди­те пло­щадь квад­ра­та,

если его диа­го­наль равна 1см .

400

Най­ди­те пло­щадь квад­ра­та,

если его диа­го­наль равна 1см .

Ответ: 0,5 см 2

НАЗАД

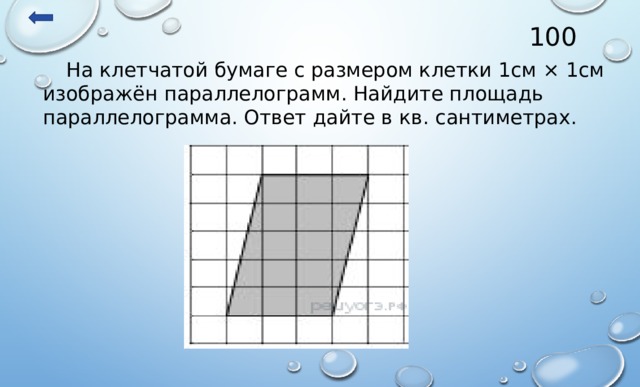
100

На клетчатой бумаге с размером клетки 1см × 1см изображён параллелограмм. Найдите площадь параллелограмма. Ответ дайте в кв. сантиметрах.

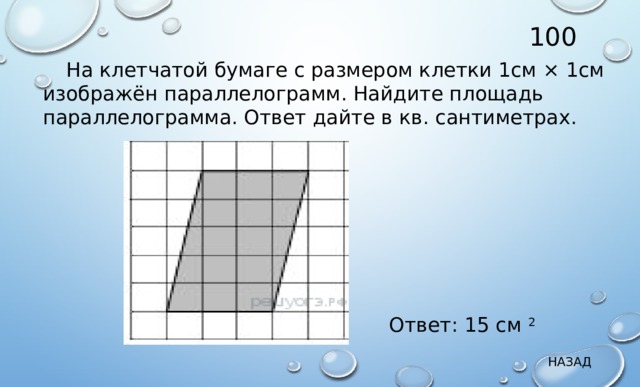
100

На клетчатой бумаге с размером клетки 1см × 1см изображён параллелограмм. Найдите площадь параллелограмма. Ответ дайте в кв. сантиметрах.

Ответ: 15 см 2

НАЗАД

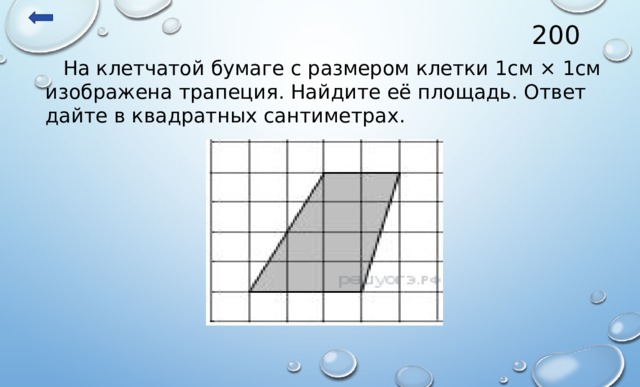
200

На клетчатой бумаге с размером клетки 1см × 1см изображена трапеция. Найдите её площадь. Ответ дайте в квадратных сантиметрах.

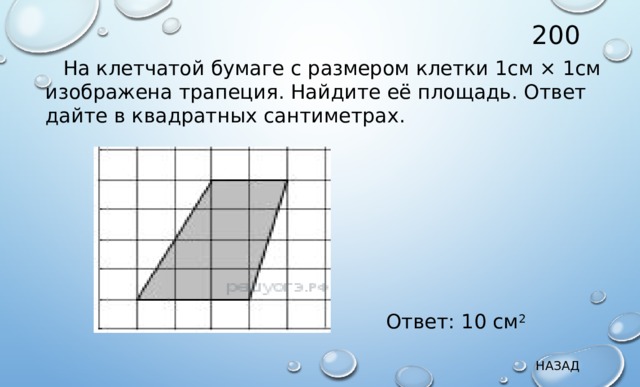
200

На клетчатой бумаге с размером клетки 1см × 1см изображена трапеция. Найдите её площадь. Ответ дайте в квадратных сантиметрах.

Ответ: 10 см 2

НАЗАД

Переход хода

300

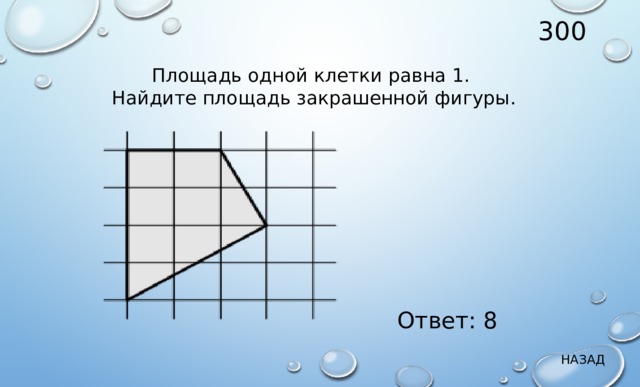
Пло­щадь одной клет­ки равна 1.

Най­ди­те пло­щадь за­кра­шен­ной фи­гу­ры.

300

Пло­щадь одной клет­ки равна 1.

Най­ди­те пло­щадь за­кра­шен­ной фи­гу­ры.

Ответ: 8

НАЗАД

400

На клетчатой бумаге с размером клетки 1см × 1см изображен ромб. Найдите площадь ромба.

Ответ дайте в квадратных сантиметрах

400

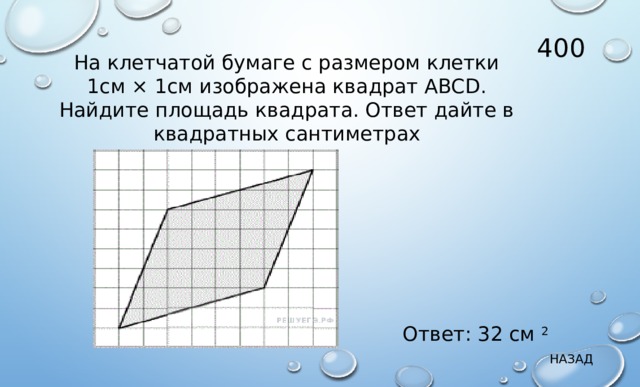
На клетчатой бумаге с размером клетки 1см × 1см изображена квадрат ABCD. Найдите площадь квадрата. Ответ дайте в квадратных сантиметрах

Ответ: 32 см 2

НАЗАД

Переход хода

100

Напишите формулу

нахождения площади прямоугольника

100

Напишите формулу

нахождения площади прямоугольника

Ответ: S=a

НАЗАД

200

Напишите формулу

нахождения площади параллелограмма

200

Напишите формулу

нахождения площади параллелограмма

Ответ: S=a

НАЗАД

300

Напишите формулу

нахождения площади трапеции

300

Напишите формулу

нахождения площади трапеции

Ответ: S=

НАЗАД

Переход хода

400

Площадь какой фигуры можно найти по данной формуле:

400

Площадь какой фигуры можно найти по данной формуле:

Ответ: треугольник

НАЗАД

100

Что называют диагональю многоугольника?

100

Что называют диагональю многоугольника?

Ответ: Отрезок, соединяющий любые две несоседние вершины, называют диагональю многоугольника

НАЗАД

200

В па­рал­ле­ло­грам­ме  ABCD  про­ве­де­на

диа­го­наль  AC . Угол  DAC  равен 47°,

а угол  CAB  равен 11°.

Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма  ABCD .

Ответ дайте в градусах.

200

В па­рал­ле­ло­грам­ме  ABCD  про­ве­де­на

диа­го­наль  AC . Угол  DAC  равен 47°,

а угол  CAB  равен 11°.

Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма  ABCD .

Ответ дайте в градусах.

Ответ: 122 0

НАЗАД

Переход хода

300

Площадь квадрата 24 см 2

Выразите площадь этого квадрата

в квадратных дециметрах

300

Площадь квадрата 24 см 2

Выразите площадь этого квадрата

в квадратных дециметрах

Ответ: 0,24 дм 2

НАЗАД

400

Что такое

«Египетский треугольник»?

400

Что такое

«Египетский треугольник»?

Ответ:

НАЗАД

100

Определите, сколь­ко необходимо за­ку­пить пленки 

  для гид­ро­изо­ля­ции садовой дорожки,

изоб­ра­жен­ной на рисунке,

если её ши­ри­на везде одинакова.

100

Определите, сколь­ко необходимо за­ку­пить пленки 

  для гид­ро­изо­ля­ции садовой дорожки,

изоб­ра­жен­ной на рисунке,

если её ши­ри­на везде одинакова.

Ответ: 13 м 2

НАЗАД

200

Площадь пря­мо­уголь­но­го

земельного участ­ка равна 9 га,

ши­ри­на участка равна 150 м.

Най­ди­те длину этого участ­ка в метрах.

200

Площадь пря­мо­уголь­но­го

земельного участ­ка равна 9 га,

ши­ри­на участка равна 150 м.

Най­ди­те длину этого участ­ка в метрах.

Ответ: 600м

НАЗАД

300

Глубина бас­сей­на со­став­ля­ет 2 метра,

ши­ри­на — 10 метров, а длина — 25 метров.

Най­ди­те сум­мар­ную пло­щадь

бо­ко­вых стен и дна бас­сей­на

(в квад­рат­ных метрах).

300

Глубина бас­сей­на со­став­ля­ет 2 метра,

ши­ри­на — 10 метров, а длина — 25 метров.

Най­ди­те сум­мар­ную пло­щадь

бо­ко­вых стен и дна бас­сей­на

(в квад­рат­ных метрах).

Ответ: 390 м 2

НАЗАД

400

Сколь­ко по­тре­бу­ет­ся ка­фель­ных

пли­ток квад­рат­ной формы

со сто­ро­ной 20 см,

чтобы об­ли­це­вать ими стену,

име­ю­щую форму пря­мо­уголь­ни­ка

со сто­ро­на­ми 3 м и 4,4 м?

400

Сколь­ко по­тре­бу­ет­ся ка­фель­ных

пли­ток квад­рат­ной формы

со сто­ро­ной 20 см,

чтобы об­ли­це­вать ими стену,

име­ю­щую форму пря­мо­уголь­ни­ка

со сто­ро­на­ми 3 м и 4,4 м?

Ответ: 330

НАЗАД

Финал

Обожаю задачи

Теорема

Художественная галерея

Высказывание

Шифровка

Конструирование

Грамотей

Шифровка

Расшифруйте слова

и назовите лишнее:

аачдза

веслуои

еирнеше

ктадрва

еттов

Шифровка

Расшифруйте слова

и назовите лишнее:

аачдза - задача

веслуои -условие

еирнеше - решение

ктадрва - квадрат

еттов -ответ

назад

Теорема

Доказательство этой теоремы учащиеся средних веков считали очень трудным и называли его Dons asinorum- ослиный мост, или elefuga- бегство "убогих", так как некоторые "убогие" ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому "ослами", были не в состоянии преодолеть теорему, служившую для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теорему , учащиеся называли ее также "ветряной мельницей", составляли различные стихи , рисовали карикатуры. Ходили легенды, что в честь этого открытия этой теоремы автор принес в жертву 100 быков.

Сформулируйте теорему, о которой идет речь.

Теорема

Ответ: теорема Пифагора – квадрат гипотенузы равен сумме квадратов катетов.

назад

Высказывание

«Математику уже затем учить надо, что она ум  в порядок приводит»

Высказывание

«Математику уже затем учить надо, что она ум  в порядок приводит»

М.В. Ломоносов

назад

Конструирование

Из двух равных прямоугольных треугольников составьте параллелограмм, не являющийся прямоугольником

назад

Художественная галерея

Назовите самую известную

в мире картину,

где изображен четырехугольник

(не забудьте упомянуть автора)

Художественная галерея

Черный квадрат

Автор К. Малевич,

1915 год

назад

Обожаю задачи

Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см

Обожаю задачи

Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см

Ответ: сторона 13 см, площадь 120 см 2

назад

Грамотей

назад