20.05 2020 р. 7 клас. Геометрія. Повторення. Елементарні геометричні фігури та їх властивості

Назва нового предмету — «геометрія» — бере початок від давньогрецьких слів «земля» та «вимірюю» і в перекладі з грецької означає «землемірство». Геометрія є однією з найдавніших наук. Вона виникла у зв'язку з практичною необхідністю у вимірах, завдяки відновленню меж земельних ділянок, будівництву доріг та споруд. Нині ми знаємо геометрію як науку, що вивчає властивості геометричних фігур. Основними геометричними фігурами є точка і пряма, які можна уявити: точку — як найпростішу нескінченно малу фігуру, уявлення про яку можна отримати, якщо на аркуш паперу натиснути добре загостреним олівцем або на шкільну дошку — добре загостреним шматком крейди, а пряму — як нескінченну тонку натягнуту нитку, яка тягнеться безмежно в обидві сторони. За допомогою цих основних геометричних фігур можна визначити всі інші фігури. 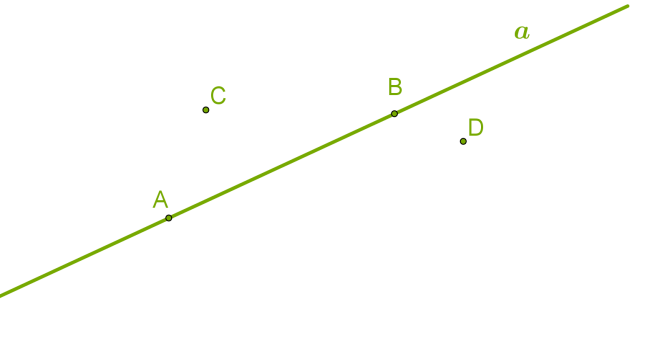Точки позначаються великими латинськими буквами, а прямі — маленькими. Словесно описати взаємне розташування точок і прямої можна по-різному: 1. Точка розташована (лежить) на прямій, або пряма проходить (проведена) через точку. 2. Точка не розташована (не лежить) на прямій, або пряма не проходить (не проведена) через точку. У геометрії ці факти записуються символічно: 1. Точки A і B розташовані (лежать) на прямій a, або пряма a проходить (проведена) через точки A і B: A∈a і B∈a. 2. Точки C і D не розташовані (не лежать) на прямій a, або пряма a не проходить (не проведена) через точки C і D: C∉a і D∉a. Одна з найважливіших аксіом у геометрії. Через будь-які дві точки можна провести пряму, і до того ж тільки одну. Отже, іноді позначити пряму можна і двома великими латинськими буквами, наприклад пряма AB, оскільки жодна інша пряма через ці дві точки не може бути проведена. 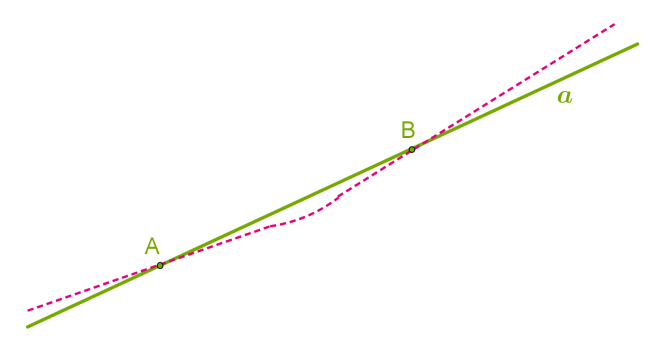Отже, дві різні прямі можуть мати лише одну спільну точку й перетинатися або не мати жодної спільної точки і ніколи не перетинатися. 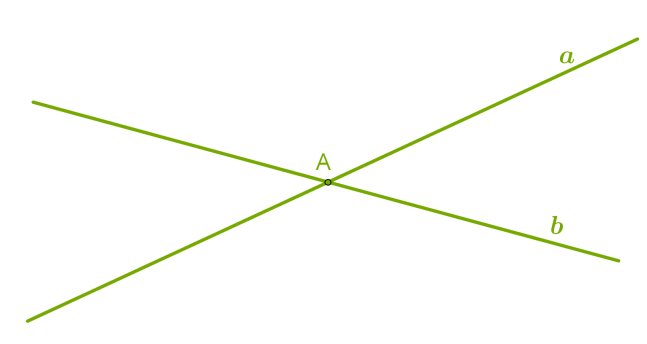Символічно записуємо: a∩b = A. 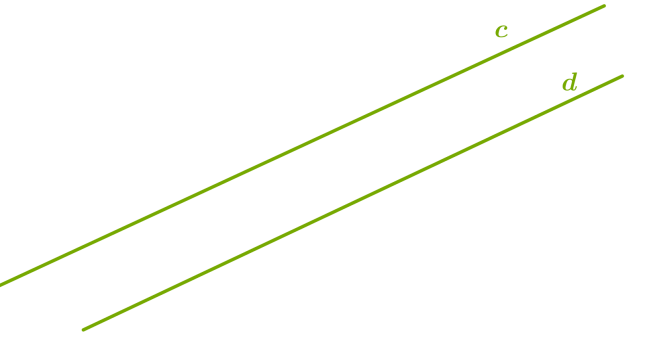Символічно записуємо a∥b. Частина прямої, що складається з двох даних точок цієї прямої й усіх точок, що лежать між ними, називається відрізком. 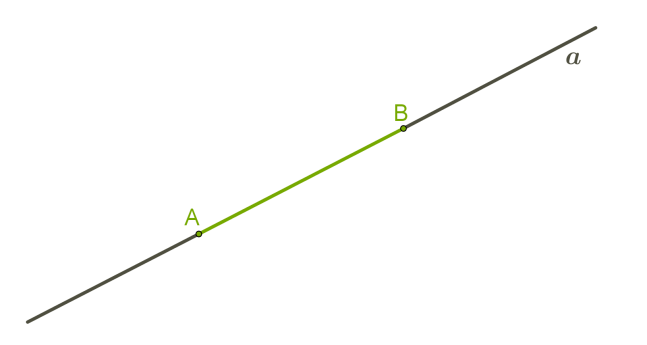Символічно записуємо: відрізок AB Уважно подивися на рисунок! 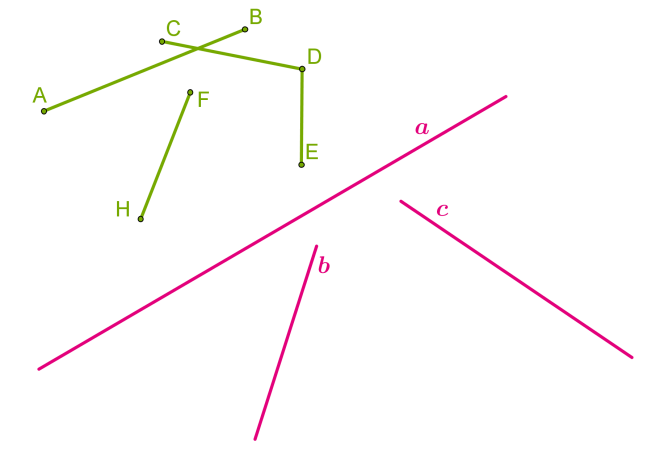Зверни увагу! 1. Відрізки AB і CD перетинаються, відрізки CD і DE мають спільну точку, відрізки AB і HF, AB і DE, CD і HF, HF і DE не перетинаються. 2. Прямі a, b і c перетинаються. Оскільки ми уявляємо пряму як нескінченну, що простягається в обидві сторони, рано чи пізно ці прямі перетнуться (попри те, що на малюнку цього не видно). Ми бачимо лише частини нескінченних прямих.

Точка, що лежить на прямій, ділить пряму на дві частини, кожна з яких називається променем, що виходить із цієї точки. Цю точку називають початком кожного з променів.

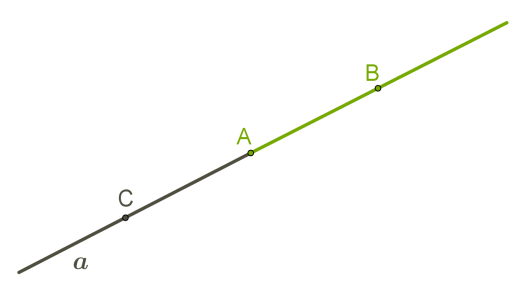
Точка A ділить пряму a на два промені. Оскільки важливо розуміти, який із променів розглядаємо, поставимо на прямій іще дві точки: B і C. Назвемо промені: промінь AB і промінь AC.

Зверни увагу! Першою завжди називають початкову точку променя.

На цьому рисунку кожна з точок може бути початковою точкою певного зображеного променя. З кожної точки виходять два промені в протилежні напрямки і, подібно до прямої, продовжуються нескінченно.

Зверни увагу! Промінь BC — той самий промінь AC, але промінь BC відрізняється від променя AC. Ці промені мають певну спільну частину.

Два різні промені однієї прямої зі спільною початковою точкою називаються доповняльними променями.

ВА та ВС — доповняльні промені з початком у точці В.

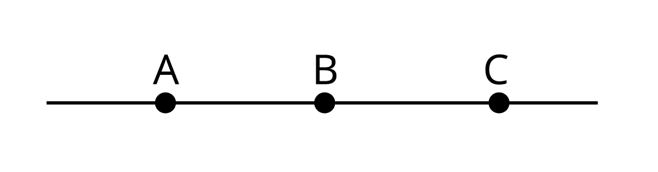
Зверни увагу! Об'єднавши промені СА та АС, ми також отримаємо пряму АС. Проте ці промені не є доповняльними: у них немає спільного початку.

Кут — геометрична фігура, яка складається з точки і двох променів, що виходять із цієї точки. Ці промені називають сторонами кута, а їхній спільний початок — вершиною кута.

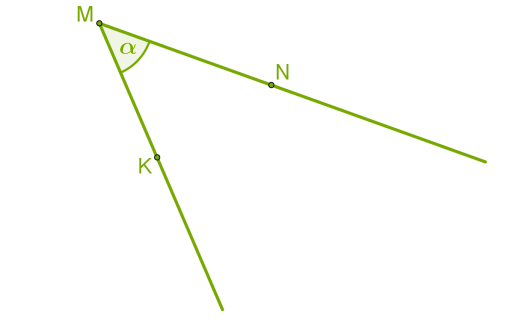
Кут позначають великими латинськими буквами, наприклад, ∠KMN, або малими грецькими буквами, наприклад, α.

Зверни увагу! Кут ∠KMN можна назвати також ∠NMK, але буква, що позначає вершину, завжди пишеться посередині.

Іноді кут можна позначити тільки однією великою латинською буквою вершини, цифрою або назвами променів — малими латинськими буквами, наприклад, ∠M, ∠1 або ∠mn.

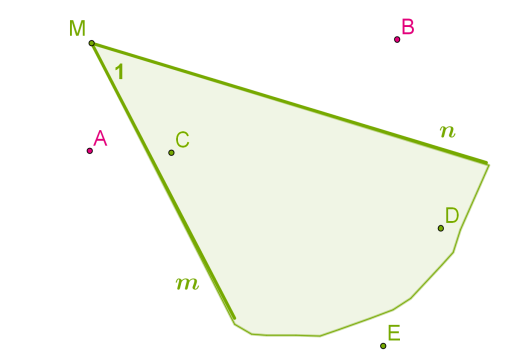
Промені n і m зі спільним початком у точці M ділять площину на дві частини: внутрішню і зовнішню область кута.

Кутом також можна називати промені зі спільним початком разом із внутрішньою областю. Тоді точки A і B не належать куту ∠M, а точки C, D і E належать куту ∠M.

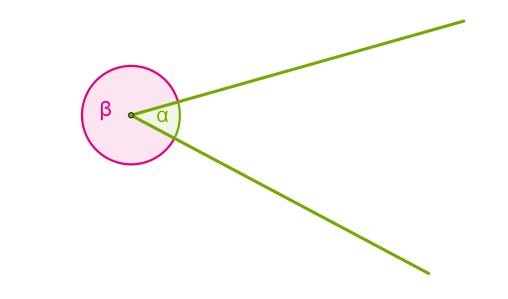
Якщо провести два промені, що виходять із однієї точки, то внутрішня область утворює один кут, а зовнішня область — інший.

Якщо обидві сторони кута лежать на одній прямій, кут називається розгорнутим.

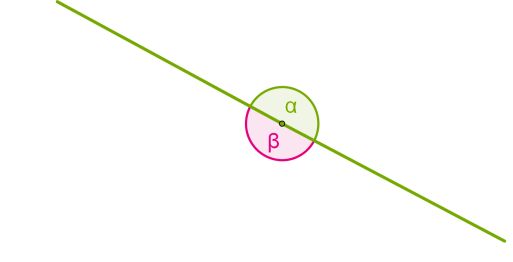
Внутрішньою областю розгорнутого кута можна вважати будь-яку з двох частин, на які він ділить площину.

Якщо у внутрішній області кута провести промінь із початком у вершині цього кута, то промінь поділить кут на два кути.

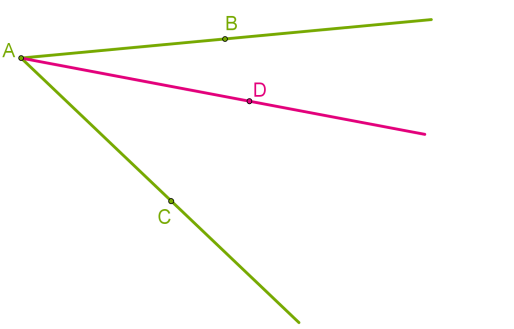
У такому випадку важливо правильно називати кути, оскільки ми маємо даний кут і дві його частини.

Наприклад, не зовсім зрозуміло, про який кут ідеться, якщо записано ∠A. Краще використовувати три великі букви, тоді назви кутів будуть зрозумілі: ∠CAB, ∠CAD, ∠DAB.

20.05.2020 р. Скласти конспект матеріалу. Повторити § 1 - 3. Виконати вправу № 809.