5 Система произвольных сил

• ГПОУ «Читинский техникум отраслевых технологий и бизнеса»

Презентация по технической механике

на тему « Плоская система произвольных сил »

• Разработал: преподаватель Батуев Б. Н.

• Чита - 2015

ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНЫХ СИЛ

• Лемма о параллельном переносе силы
•   Механическое состояние твердого тела не нару­шится, если данную силу перенести параллельно самой себе в произвольную точку тела, добавив при этом пару, момент которой равен моменту данной силы относительно новой точки приложении.
• Возьмем тело, находящееся под действием некоторой систе­мы сил, в числе которых есть сила Р, приложенная в точке А (рис.). Выберем произвольную точку О, которую назовем центром приведения, и на основании аксиомы IV при­ложим в этой точке две равные силы Б" и Р", параллельные данной силе К, причем
• Систему сил (Р, Р', Б 1 "), эквивалентную силе Р, представим как силу Р, перенесенную параллельно самой себе в произвольно выбранный центр приведения О, и пару (Р, Р"), момент которой равен моменту данной силы относительно центра приведения О, являющегося новой точкой приложения силы:
• М(Р, Я") = Ра = М 0 (Я).
• Лемма доказана.
• Описанный выше перенос силы можно показать на примере. Рассмотрим колесо А радиуса г, вращающееся на оси в подшип­никах (рис.). Пусть к ободу колеса по касательной при­ложена сила Р (такую силу называют окружной).
• Для определения действия силы Р на колесо и подшипники применим доказанную лемму и перенесем эту силу параллельно самой себе на ось колеса. В результате получим силу Р' = Р. вызывающую давление на подшипники, и пару сил (Р, Р") с моментом, равным Рг, которая будет вращать колесо.

• Приведение плоской системы произвольно расположенных сил к данному центру
• Приведением системы сил называется замена ее другой системой, эквивалентной первой, но более простой.
• Теорема. Плоская система произвольно расположенных сил в общем случае эквивалентна одной силе, приложенной в центре приведения, и одной паре.
• Пусть дана плоская система п произвольно расположенных сил (Р 1? Р 2 , Р 3 , ...,?„_!, Р„). Перенесем параллельно все силы в произвольно выбранный в плоскости действия сил центр приведения О, добавив при этом п пар (рис.).
•  
• Моменты этих пар /?/!, т 2 , т 3 , ..., т„ равны моментам данных сил относительно центра приведения О.
• Вместо заданной систе­мы п произвольно рас­положенных сил мы полу­чили систему п сил, при­ложенных в центре приве­дения, равных данным си­лам по модулю и оди­наковых с ними по на­правлению, и систему п присоединенных пар:
• Эта новая система эквивалентна данной.
• Плоская система сил, приложенных в одной точке, экви­валентна одной силе, которая равна векторной сумме этих сил и приложена в той же точке, следовательно,
• или
• Г = ЕР.
• ж гл ж г
• Эту силу назовем главным вектором данной системы. Главный вектор плоской системы произвольно расположенных сил равен векторной сумме всех сил системы и приложен в центре приведения.
• Графически главный вектор выражается замыкающей сторо­ной силового многоугольника, построенного на данных силах. Аналитически модуль главного вектора можно вычислить по формуле
• а направляющий косинус — по формуле
• Плоская система пар эквивалентна одной паре, момент которой равен алгебраической сумме моментов данных пар, следовательно,
• или
• Эту пару с моментом М гл назовем главным моментом заданной системы сил.
• Главный момент плоской системы произвольно расположен­ных сил равен алгебраической сумме моментов всех сил системы относительно центра приведения.
• Таким образом, всякая плоская система сил в общем случае эквивалентна системе, состоящей из силы и пары сил, следовательно, теорема доказана.
• Не следует считать, что главный вектор и главный момент имеют чисто формальное значение, введенное для удобства доказательства, и что их можно найти только с помощью вычислений. Нередко отдельно действующие на тело силы определить трудно или невозможно, а главный вектор или главный момент этих сил найти сравнительно легко. Так, например, число точек контакта и модули сил трения между вращающимся валом и подшипником скольжения, как правило, неизвестны, но главный момент этих сил можно определить простым измерением; второй пример: в характеристику электро­двигателя входит не сила, с которой статор действует на ротор, а вращающий момент.

• Свойства главного вектора и главного момента
•   Свойства главного вектора и главного момента заключа­ются в следующем: модуль и направление главного вектора данной системы не зависят от выбора центра приведения, так как при любом центре приведения силовой многоугольник, построенный на данных силах, будет один и тот же; величина и знак главного момента в общем случае зависят от выбора центра приведения (кроме одного случая, о котором будет сказано в § 5.4), так как при перемене центра приведения меняются плечи сил, а модули их остаются неизменными;
• главный вектор и равнодействующая системы сил векторно равны, но в общем случае не эквивалентны. Пусть известны главный вектор Р гл и главный момент М гл какой-то плоской системы сил (рис. 5.4). Опре­делим равнодействующую этой системы.
• Пользуясь известным свой­ством пары сил, преобразуем главный момент М гл так, что­бы силы пары Р и Р Е были параллельны и по модулю равны главному вектору Р гл :
• '",, Р), Рис. 5.4
• причем сила Р приложена к точке О противоположно Р гл .
• Далее систему (Р гл , Г), как взаимно уравновешенную, от­бросим:
• (Р гл , Л/ ГЛ НР ГЛ , Р, Р^Р,.
• В результате получили одну силу Р Е , эквивалентную главному вектору и главному моменту, т. е. равнодействующую системы, причем
• Р Г = Р
• * Е * гл'
• Модуль равнодействующей
• а положение линии действия равнодействующей определяется плечом (1 по формуле
• В результате можно считать установленным, что главный вектор и равнодействующая векторно равны, но не эквива­лентны;
• 4) главный вектор и равнодействующая эквивалентны лишь в частном случае, когда главный момент системы равен нулю', последнее возможно в случае, когда центр приведения нахо­дится на линии действия равнодействующей.
• Из 5.4 видно, что момент равнодействующей Р Е
• относительно центра приведения О равен моменту М гл пары (Р Е , Р), т. е. главному моменту данной системы:
• Так как М ГЛ = ЕМ 0 (Р,-), а за центр приведения можно взять любую точку плоскости действия сил данной системы, то всегда имеем
• Полученная формула является математическим выражением теоремы о моменте равнодействующей.
• Теорема. Момент равнодействующей силы относительно какой-либо точки, расположенной в плоскости действия сил, равен алгебраической сумме моментов составляющих сил отно­сительно той же точки.
• Теорему о моменте равнодействующей впервые доказал французский ученый Вариньон (1654 — 1722), поэтому ее назы­вают теоремой Вариньон а.
• Применим доказанную теорему для определения положения линии действия равнодействующей Р Е плоской системы п парал­лельных сил:
• (Б\, Р 2 , Р 3 , ..., Р^^Р,. 38
• Выберем какую-либо точку О плоскости действия сил за центр моментов и согласно теореме Вариньона запишем
• где А — плечо равнодействующей ре относительно точки О. Из последнего равенства определяем плечо А\
• так как, согласно § 3.2, ^ = Х^-
• Чтобы установить, в какую сторону от точки О следует на перпендикуляре к линиям действия сил отложить плечо А, следует учесть, во-первых, направление вектора Р Е и, во-вторых, знак ^

Различные случаи приведения плоской системы произвольно расположенных сил

• Изучив свойства главного вектора и главного момента, укажем четыре возможных случая приведения плоской системы произвольно расположенных сил:
• Р гл ^0, М гл ^0, т. е. главный вектор и главный момент не равны нулю. В этом случае система сил эквивалентна равнодействующей, которая равна по модулю главному век­ тору, параллельна ему, направлена в ту же сторону, но по другой линии действия (см. § 5.3, п. 3).
• Р гл ^0, М гл = 0. В этом случае система сил эквивалентна равнодействующей, линия действия которой проходит через центр приведения и совпадает с главным вектором.
• 3. Р гл = 0, М гл ^0. В этом случае система эквивалентна паре. Так как модуль и направление главного вектора во всех случаях не зависят от выбора центра приведения, то в рассматриваемом случае величина и знак главного момента тоже не зависят от центра приведения, ибо одна и та же система сил не может быть эквивалентна различным парам.
• 4. Р гл = 0, М гл = 0. В этом случае система сил эквивалентна нулю, т. е. находится в равновесии.

Аналитические условия равновесия плоской системы произвольно расположенных сил

Для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси координат х и у равнялись нулю и чтобы алгебраическая сумма моментов этих сил относительно любой точки плоскости также равнялась нулю.

Т. е. Σ Х = 0, Σ Y = 0, Σ M = 0.

Для равновесия плоской системы произвольных сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси координат х, у и алгебраическая сумма моментов этих сил относительно любой точки равнялись нулю.

Т. е. Σ Х = 0 (1), Σ Y = 0 (2), Σ M = 0 (3).

Для равновесия плоской системы произвольных сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси координат х, у и алгебраическая сумма моментов этих сил относительно любой точки равнялись нулю.

Т. е. Σ Х = 0 (1), Σ Y = 0 (2), Σ M(О) = 0 (3).

• Отметим, что выведенные ранее условия равновесия системы сходящихся сил, системы параллельных сил и системы пар являются частными случаями условий равновесия, полученных в этом параграфе.
• При решении некоторых задач бывает целесообразно вместо одного или двух уравнений проекций составлять уравнения моментов.
• Если заменить одно уравнение проекций, то условия равновесия плоской системы произвольно расположенных сил будут выглядеть так:
• Х*=о, ]Гм л =о, ^м в =о.
• Однако следует помнить, что эти условия становятся недостаточными для равновесия, когда центры моментов А и В лежат на одном перпендикуляре к оси х; в этом случае даже при выполнении указанных условий система сил может иметь равнодействующую, проходящую через эти точки, и, следовательно, не быть в равновесии.
• Если заменить два уравнения проекций, то условия равно­весия плоской системы произвольно расположенных сил будут выглядеть так:
• Однако эти условия становятся недостаточными для равно­весия, когда центры моментов А, В и С лежат на одной прямой; в этом случае даже при выполнении указанных условий система сил может иметь равнодействующую, про­ходящую через эти точки, и, следовательно, не быть в рав­новесии.
• Условия равновесия плоской системы параллельных сил являются частным случаем условий равновесия, выведенных в этом параграфе. Если ось у расположить параллельно линиям действия системы параллельных сил, то уравнение равновесия ^Х=0 обратится в тождество, а Х^ = Х^' т - е -алгебраическая сумма проекций сил системы на ось у будет равна алгебраической сумме этих сил. Тогда условия равновесия плоской системы параллельных сил запишутся следующим образом:
• и сформулируются так: для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы алгебраи­ческая сумма всех сил равнялась нулю и чтобы алгебраическая сумма моментов всех сил относительно любой точки плоскости также равнялась нулю.
• Так как все виды аналитических условий равновесия действи­тельны для любых прямоугольных осей координат, то в процес­се решения одной задачи или при проверке решения оси координат можно изменить, т. е. одни уравнения проекций сил составить для одной системы координат, а другие — для новой системы координат. Этот прием в некоторых случаях упрощает решение или проверку решения задач. При этом следует помнить, что число уравнений равновесия, составля­емых для решения (но не для проверки решения), не должно быть больше числа условий равновесия, соответствующих системе сил, рассматриваемых в задаче.
• При решении задач статики аналитическим способом целе­сообразно составлять уравнения равновесия так, чтобы в каж­дом из них была только одна неизвестная величина. Во многих случаях этого можно достигнуть, если рационально выбрать оси координат и центры моментов.

Задача № 2. Вариант 40, схема IV

Балка шарнирно закреплена в точке А и удерживается в горизонтальном положении стержнем ВС, нагружена силами F 1 и F 2 =0,6F 1 . Определить реакцию стержня ВС и шарнира А. Числовые значения своего варианта взять из таблиц. Геометрические размеры балки изобразить в масштабе.

Дано: F 1 = 5кН; F 2 =0,6F 1 = 3кН;

а= 2,8м, в = 0,4м α = 42⁰.

Х А = ? У А = ? R С = ?

Задача № 2. Вариант 40, схема IV

Дано: F 1 = 5кН; F 2 =0,6F 1 = 3кН;

а= 2,8м, в = 0,4м α = 42⁰.

ХА = ? УА = ? RС = ?

Решение: 1) Балку освобождаем от связей и заменяем силами их реакций (реактивными силами) согласно опорных реакций шарниров и невесомых стержней. Эти силы реакции нам необходимо определить.

2) Составляем уравнения равновесия для плоской произвольно расположенной системы сил и решаем их. …

3) Производим проверку правильности решения задачи. …

Домашнее задание. Решить аналогичную задачу №2 в соответствии со своим вариантом. № варианта = № по списку в классном журнале, стр 1. Срок решения = 1 неделя.

Вариант

№ схемы

a

1

I

b

2

м

F 1

I

3

2,3

α⁰

0,5

3,2

I

4

1,2

I

3,8

5

3,3

2,6

65

I

6

2,8

1,2

7

60

I

1,8

1,8

0,8

I

1,8

62

0,2

2,8

8

9

1,4

I

64

1,6

3,3

10

58

2,1

I

1,6

3,6

2,5

55

I

2,5

1,5

52

2,6

1,8

1,2

3,2

0,8

50

48

2,8

45

11

12

II

II

3

13

14

1,5

3

II

2

II

4

3,5

15

II

1,4

16

30

5

2,8

32

II

0,8

17

2,4

6

II

5

18

3,1

0,6

35

1,1

II

40

4

2,7

19

45

II

2,6

3

0,5

20

50

II

1,2

2

2,5

1,5

3

52

3,4

55

1,3

6

2

60

64

21

22

III

23

3,8

III

1,2

24

2,6

III

25

3

2,5

0,5

III

1,2

2,5

70

26

III

2,4

3

27

3,5

0,8

65

III

28

4

1,6

60

III

3,6

4,5

29

55

1,6

III

3,2

3,5

1,2

30

50

III

4,8

1,5

5

2,8

45

III

6

0,5

2,6

40

5,5

1,2

35

2

30

48

31

32

IV

33

2,5

IV

34

0,5

2,4

IV

35

4

IV

3,1

1,4

IV

50

36

3,2

6

1,2

8

1,5

37

3,1

IV

40

5

0,5

38

30

2,5

IV

39

4,5

IV

0,5

2,5

35

1,2

5,5

40

45

3,3

IV

3

1,5

0,8

48

IV

3,5

0,5

55

2,8

2,5

60

0,4

5

65

42

Задача № 1. Вариант 40, схема IV

Определить реакции опор А и В балки, нагруженной, как показано на рис. Данные для своего варианта выбрать из таблиц. Геометрические размеры балки изобразить в масштабе.

Дано: F 1 = 20кН; F 2 =20кН; М=15кН∙м; q=3кН/м

а= 2м, в = 1,5м с = 1,2м.

RА = ? ХВ = ? УВ = ?

Решение: Последовательность решения аналогична предыдущей задаче.

1) Балку освобождаем от связей и заменяем силами их реакций (реактивными силами) согласно опорных реакций шарниров и невесомых стержней. Эти силы реакции нам необходимо определить.

2) Составляем уравнения равновесия для плоской произвольно расположенной системы сил и решаем их.

…

3) Производим проверку правильности решения задачи.

…

Домашнее задание. Решить аналогичную задачу №1 в соответствии со своим вариантом. № варианта = № по списку в классном журнале, стр 1. Срок решения = 1 неделя.

Вариант

№ схемы

1

a

I

м

2

b

1,5

3

I

c

1,2

4

I

1,5

F 1

1,5

2,3

2

5

I

кН

F 2

0,8

1,8

12

1,5

I

6

M

1,4

2,4

20

2,2

кН*м

10

I

7

q

16

2,5

40

1

кН/м

6

8

1,2

I

8

8

2,3

2,6

2

9

8

20

I

10

25

10

6

10

1,8

2,5

I

0,5

15

0,5

0,8

12

10

12

I

2,5

1,2

10

14

2,1

40

1,1

18

5

20

3,5

3,2

8

8

6

12

20

0,5

5

15

8

5

24

10

10

12

12

10

10

11

12

II

II

13

2,4

14

II

2,5

2,6

2,4

II

0,5

15

2,4

2,3

0,8

20

16

2,2

II

1,8

18

II

2,3

1,2

17

1,8

II

6

1,8

18

1,8

1,2

16

2,2

II

2

8

15

1,8

19

12

6

1

1,6

II

20

8

14

1,5

1,6

5

12

2,1

6

10

II

2

15

1,2

5

14

8

1,5

2,2

1,4

8

2

1,2

6

18

13

1,4

10

12

5

1,5

12

0,8

15

4

15

1,4

12

7

1,4

12

4

3

21

22

III

23

1,4

III

1,5

24

1,8

III

25

2,5

III

1,8

1,4

10

26

2,5

2,5

2

III

12

2

1,5

27

1,4

12

III

12

1,1

28

1,2

20

10

III

1,2

4

1,5

29

14

13

14

2,1

III

2,5

30

11

1,5

20

III

2

1,5

18

0,8

3

10

0,8

1,5

22

1,3

22

III

3,5

12

5

1,3

18

1,3

8

1,2

4

12

6

1,2

13

1,2

14

10

3

14

10

2

15

12

5

16

12

4

10

4

31

IV

32

0,8

33

IV

1,5

34

IV

1,8

0,8

35

0,5

1,8

IV

8

0,6

IV

36

0,9

0,9

0,8

10

37

1,5

0,5

IV

10

14

0,5

38

0,5

0,5

18

IV

12

1,5

39

2

15

1,2

20

0,9

12

IV

18

1,5

1,5

40

1,6

10

IV

16

3

4

18

1

16

2,5

1

IV

8

2,5

2,5

10

5

16

10

2

1,1

2

1,5

14

8

12

12

3

1,2

12

12

18

4

16

20

5

10

20

2

15

3

• Пример 1. Горизонтальная балка, поддерживающая балкон, подвергается действию равномерно распределенной нагрузки интенсивностью q =2 кН/м. На балку у свободного конца С передается нагрузка от колонны Р=2 кН. Расстояние от оси колонны до стены l =1,5м. Определить реакции заделки А .

Дано: q =2 кН/м

Р=2 кН

l =1,5м

R = ?

т = ?

Решение:

Отбросим заделку, заменим ее реакциями и рассмотрим равновесие балки. Реакции стены представляют собой реактивную силу R и реактивный момент т. Реактивная сила вертикальна, так как активные силы, действующие на балку, горизонтальных составляющих не имеют. Распределенную нагрузку заменим ее равнодействующей ql .

• Решение. Отбросим заделку, заменим ее реакциями и рассмотрим равновесие балки. Реакции стены представляют собой реактивную силу R и реактивный момент т. Реактивная сила вертикальна, так как активные силы, действующие на балку, горизонтальных составляющих не имеют. Распределенную нагрузку заменим ее равнодействующей ql .

Применим условия равновесия плоской системы параллельных сил и составим два уравнения равновесия:

Σ Fi = 0; R – q l – P = 0, откуда R = ql + P = 2 ∙10 3 ∙1,5 + 2∙10 3 = 5∙10 3 Н;

Σ M(A) = 0; m- q ll /2 - Р l =0, откуда т = Р l+ql 2 /2 = 2 ∙ 10 3 • 1,5 + 2 • 10 3 • 2,25/2 = 5,25 • 10 3 Н ∙ м.

Проверка решения, составив контрольное уравнение моментов относительно точки С:

ΣM(C) = 0; m - Rl + ql 2 /2 =0. Подставив значения, получим

5,25•10 3 – 5•10 3 •1,5 + 2•10 3 - 2,25/2 = 0. Полученное тождество 0 = 0 свидетельствует, что решение верное.

• Пример 2. Предохранительный клапан А парового котла соединен стержнем АВ с однородным рычагом СО длиной 50 см и силой тяжести 10 Н, который может вращаться вокруг неподвижной оси С; диаметр клапана d=6 см, плечо СВ = 1 см. Какой груз G нужно подвесить к концу D рычага для того, чтобы клапан сам открывался при давлении в котле p=110Н/см 2 ?

• Дано: СD = 50 см
• F = 10 Н
• d=6 см
• СВ = 7 см
• p=110Н/см 2
• G - ?

• Решение. Рассмотрим равновесие рычага СD. Реакция R в клапана будет направлена вверх и равна
• R в = pπd²/4 = 110 ∙ 10⁴ π36 ∙ 10⁻⁴/4 = 3109 Н
• Так как реакцию R с шарнира С определять не нужно, то составим уравнение моментов относительно точки С:
• ΣMc = 0; -G ∙ CD – F ∙ CD/2 + R в ∙ CB = 0.
• Подставим значения и определим G:
• G = (3109 ∙ 7 ∙ 10⁻ 2 - 10 ∙ 25 ∙ 10⁻ 2 )/(50 ∙ 10⁻ 2 ) = 430Н.

• Пример 3. На рис. схематически изображен подъемный кран. В точке D на расстоянии 5 м от оси АВ крана подвешен груз P=50кН. Сила тяжести крана G = 30 кН. Определить реакции подпятника А и подшипника В.

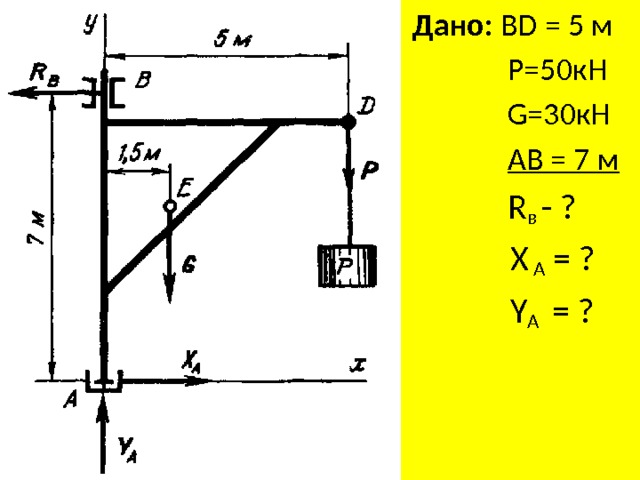
• Дано: ВD = 5 м
• P=50кН
• G=30кН
• АВ = 7 м
• R в - ?
• X A = ?
• Y A = ?

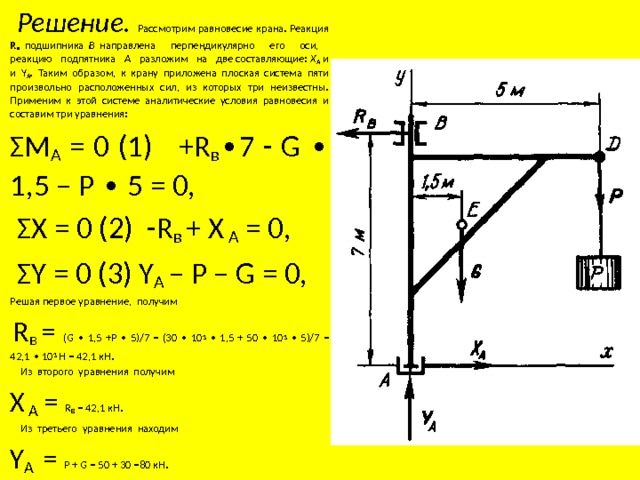
• Решение. Рассмотрим равновесие крана. Реакция R в подшипника В направлена перпендикулярно его оси, реакцию подпятника А разложим на две составляющие: Х А и и Y А . Таким образом, к крану приложена плоская система пяти произвольно расположенных сил, из которых три неизвестны. Применим к этой системе аналитические условия равновесия и составим три уравнения:
• ΣМ A = 0 (1) +R в ∙7 - G ∙ 1,5 – Р ∙ 5 = 0,
• ΣX = 0 (2) -R в + X A = 0,
• ΣY = 0 (3) Y A – P – G = 0,
• Решая первое уравнение, получим
• R в = (G ∙ 1,5 +P ∙ 5)/7 = (30 ∙ 10 3 ∙ 1,5 + 50 ∙ 10 3 ∙ 5)/7 = 42,1 ∙ 10 3 Н = 42,1 кН.
• Из второго уравнения получим
• X A = R В = 42,1 кН.
• Из третьего уравнения находим
• Y A = P + G = 50 + 30 =80 кН.

• Задача. Определить реакции опор нагруженной балки.

Дано: а = 2 м, b = 3 м, c = 1,5 м, F1 = 20 кН, F2 = 10 кН, М = 12 кН∙м, q = 4кН/м.

R А - ? (Х А - ? Y A - ?)

R В - ?

Решение:

1) На расчетной схеме расставляем направления опорных реакций.

2) Записываем общее условие равновесия:

Σ Х = 0 (1), Σ Y = 0 (2), Σ M = 0 (3).

3) Применительно к схеме записываем уравнения равновесия:

(1)… (2)… (3) …

Последовательно решаем уравнения с одним неизвестным

4) Проверяем правильность решения:

Σ M = 0 (3).

Задача. Определить реакции опор нагруженной балки.

а = 2 м, b = 3 м, c = 1,5 м,

F1 = 20 кН, F2 = 10 кН, М = 12 кН∙м, q = 4кН/м.

R А - ? (Х А - ? Y A - ?) R В - ?

Домашнее задание. Решить 3 задачи.

См методичку, стр. 28. Задачи 11 – 20. Свой вариант (№ в кл. журнале, +20, +40) выбрать из табл. 5 на стр. 30-32, столбца 2.

Свою схему выбрать на стр. 29, рис. 11.

Приятного решения !

Срок сдачи и защиты 1й задачи – на след. занятии, 2й, 3й задач– через неделю

Методичка,

стр. 29,

рис. 11

• Список использованных источников

• 1. Эрдеди А.А. Техническая механика: Теоретическая механика. Сопротивление материалов. М.: 2005.
• 2. Автор и источник заимствования неизвестен.

Конец