Информатика 10 кл. Мацегора О.П.
10 класс. Интегрированный урок по информатике и алгебре
Тема: «Полярные координаты. Построение графиков кривых в программе Microsoft Office Еxcel »
Цели урока:
1) обучающая: знакомство с полярными координатами и построением графиков в них, ознакомить учащихся с возможностью построения графиков функций в среде электронных таблиц;
2) развивающая: развитие познавательного интереса, логического мышления, внимания учащихся
3) воспитательная: воспитание усидчивости, внимательности; привитие учащимся навыка самостоятельности в работе.
Тип урока: урок повторения, обобщения и проверки знаний.
Вид урока: урок – практикум
Оборудование: проектор, компьютеры, доска
Ход урока
1) Организационная часть.
Тема нашего занятия «Полярные координаты. Построение графиков кривых в программе Microsoft Office Еxcel».Сегодня мы проводим интегрированный урок «Построение графиков функций с использованием MS Excel». Понятие функции в математическом анализе является одним из основных потому, что нас окружает множество изменяющихся величин. Многие из этих величин очень тесно связаны между собой, т.е. одни зависят от других. Функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами.
2) Мотивация.
Для исследования функций и построения графиков требуется много времени, приходится выполнять много громоздких вычислений, это не всегда удобно, но на помощь приходят компьютерные технологии. А где на практике вы, учащиеся 10 класса, можете применить это своё умение (на уроках физики, химии, математике). Вам может понадобиться умение строить графики функции с помощью компьютера при решении задач из школьного курса математики: при непосредственной задаче «построить график функции» для самопроверки, для графического решения уравнений и неравенств, для графического решения системы уравнений.
В полярной системе координат основными постоянными элементами, по отношению к которым определяется положение точки на плоскости, является точка O - полюс и ось OP, которая называется полярной осью.
Если M - произвольная точка плоскости, не совпадающая с полюсом O, то ее положение на плоскости вполне определено заданием двух чисел: r - ее расстояния от полюса, выраженного в единицах масштаба, и - угла φ, на который следует повернуть полярную ось против часовой стрелки, чтобы она совпала с лучом OM. Числа r и φ называются полярными координатами точки M.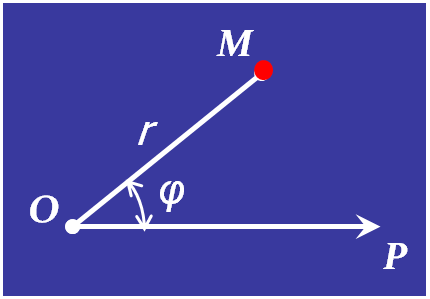
Если уравнение задано в декартовых координатах, то следует перевести его в полярные, используя формулы: X=R*COS(F), Y=R*SIN(F). Следовательно, математическая модель у нас уже есть. Рассмотрим пример построения кривой.
Задача. Построить кривую, заданную уравнением 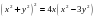
Решение. Найдем уравнение данной линии в полярных координатах.
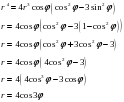
Для программы Microsoft Excel: R=4*COS(3*F)
Предположим, что угол F изменяется в интервалах от 0 до 2 . Для того, чтобы построить эту кривую наиболее точно, с малым шагом изменения угла F, как мы это делали при построении тригонометрических функций, мы выберем шаг изменения 0,1.
. Для того, чтобы построить эту кривую наиболее точно, с малым шагом изменения угла F, как мы это делали при построении тригонометрических функций, мы выберем шаг изменения 0,1.
Построим компьютерную модель исследования.
Формулы будут записаны в терминах электронных таблиц следующим образом:
А2 0,1
А3 =А2+0,1
B2 =4*COS(3*А2)
C2 =SIN(А2)
D2 =COS(А2)
E2 =B2*D2
F2 =В2*C2
Тогда получаем следующее распределение по столбцам электронной таблицы:
|
| A | B | C | D | E | F |
| 1 | F | R | SIN(F) | COS(F) | X | Y |
| 2 | 0,1 | 3,821346 | 0,099833 | 0,995004 | 3,802255 | 0,381498 |
| 3 | 0,2 | 3,301342 | 0,198669 | 0,980067 | 3,235535 | 0,655875 |
| 4 | 0,3 | 2,48644 | 0,29552 | 0,955336 | 2,375387 | 0,734793 |
| 5 | 0,4 | 1,449431 | 0,389418 | 0,921061 | 1,335014 | 0,564435 |
| 6 | 0,5 | 0,282949 | 0,479426 | 0,877583 | 0,248311 | 0,135653 |
Для построения графика выделим информационный блок E2..F63, так как аргумент F, будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 9,42, 12,56, и т. д. Получим следующий график.
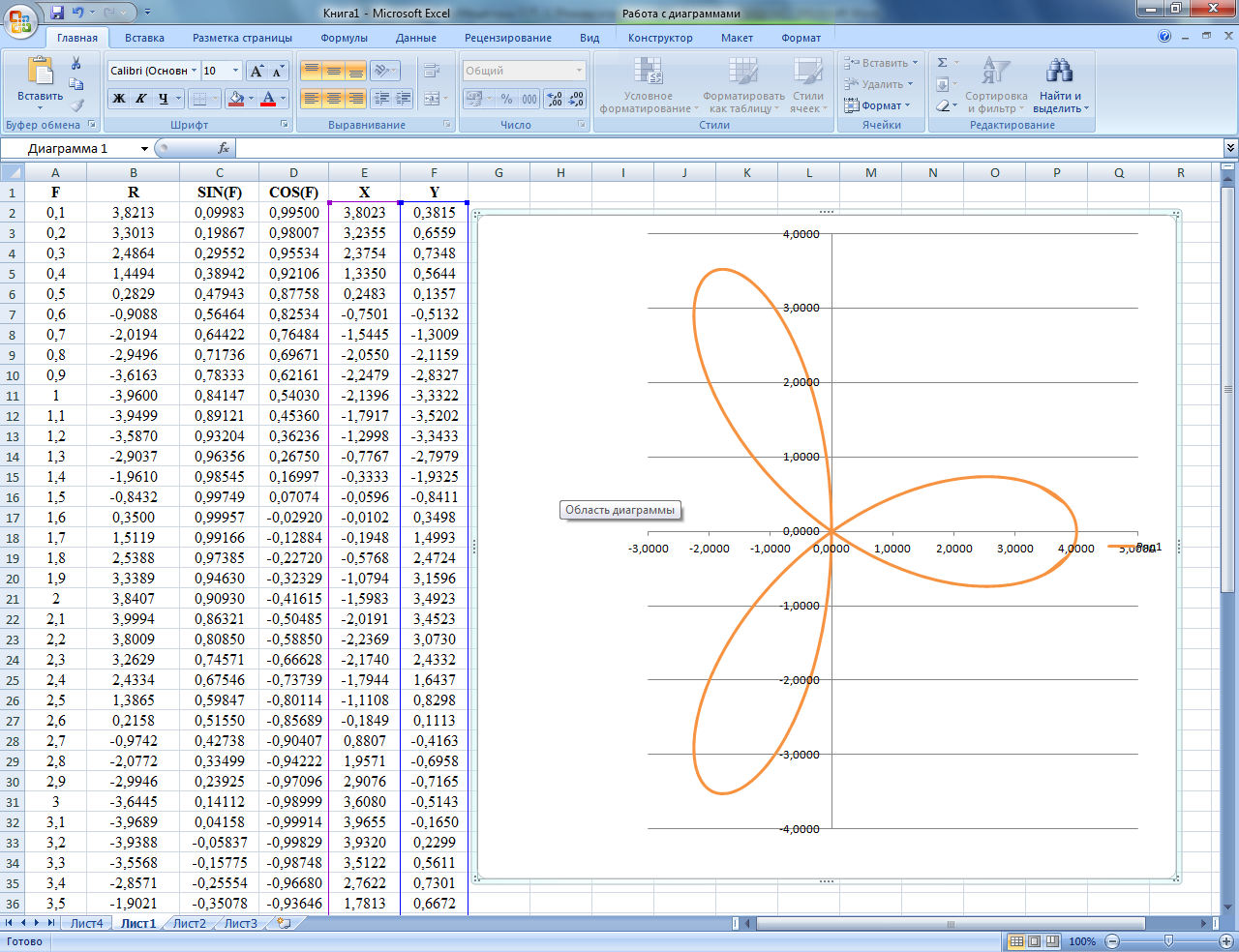
Исследование формы кривой, в зависимости от изменения значений входящих в её уравнение. Внося изменения в ячейку В2 , не меняя более ничего, мы можем получать различные виды уравнения  .
. 
Построение:
На Листы 2-4 скопировать блок А1..F63
Внести изменения в ячейки В2..В63
Для построения графика выделить информационный блок E2..F6.
Материалы для самостоятельной работы. Построение спиралей
В математике спираль — это кривая, которая огибает некоторую центральную точку или ось, постепенно приближаясь или удаляясь от неё, в зависимости от направления обхода кривой.
Спираль Архимеда может быть определена как траектория точки, участвующей одновременно в двух равномерных движениях, одно из которых совершается вдоль прямой, а другое – по окружности. Изобретение этой спирали приписывается, по некоторым источникам, Кокону Самосскому, однако свойства ее были изучены Архимедом. 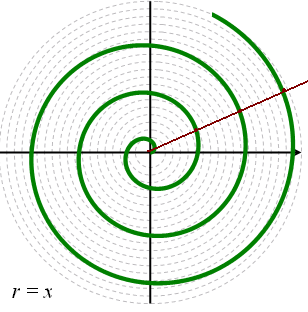
Уравнение кривой в декартовом представлении: 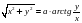 , в полярных координатах:
, в полярных координатах: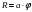 , где а - коэффициент пропорциональности (получили прямо-пропорциональную зависимость). Расстояния между соседними витками спирали есть величина постоянная и равна - а. Различают правую и левую спираль, закрученную по- или против- часовой стрелки.
, где а - коэффициент пропорциональности (получили прямо-пропорциональную зависимость). Расстояния между соседними витками спирали есть величина постоянная и равна - а. Различают правую и левую спираль, закрученную по- или против- часовой стрелки.
Применение. По спирали Архимеда идет звуковая дорожка на грампластинке. Туго свернутый рулон бумаги в профиль также представляет собой спираль Архимеда. Одна из деталей швейной машины – механизм для равномерного наматывания ниток на шпульку – имеет форму спирали Архимеда.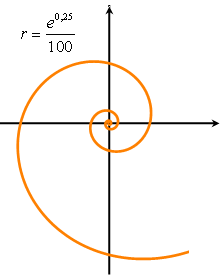
Логарифмическая спираль. В истории математики логарифмическая спираль упоминается впервые в письме Декарта к Мерсену в 1638 г., в котором Декарт определяет новую спираль как линию, отношение длины дуги которой к радиус-вектору является постоянным. Независимо от Декарта логарифмическая спираль была открыта Торичелли. Особенно много внимания логарифмической спирали уделил Я. Бернулли, назвавший ее - дивная спираль. Само же название логарифмической спирали было предложено Вариньоном. Уравнение кривой в полярных координатах: 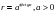 .
.
Логарифмическая спираль имеет многочисленные применения в технике, основанные на свойстве этой кривой пересекать все свои радиус-векторы под одним и тем же углом. Это свойство применяют в режущих машинах. Вращающиеся ножи в режущих машинах имеют профиль, очерченный по дуге спирали, благодаря чему угол резания остается постоянным.
Золотая спираль: 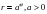 (частный случай логарифмической спирали). Эту кривую можно заметить в созданиях природы. Например, раковины многих моллюсков, улиток, рога архаров закручиваются по золотой спирали. Один из наиболее распространенных пауков, эпейра, сплетает свою паутину по золотой спирали. Cемечки в подсолнухе располагаются по золотой спирали, точно так же, как и многие галактики, в том числе и галактика Солнечной системы. В гидротехнике по золотой спирали изгибают трубу, подводящую поток воды к лопастям турбины. Благодаря этому напор воды используется с наибольшей производительностью.
(частный случай логарифмической спирали). Эту кривую можно заметить в созданиях природы. Например, раковины многих моллюсков, улиток, рога архаров закручиваются по золотой спирали. Один из наиболее распространенных пауков, эпейра, сплетает свою паутину по золотой спирали. Cемечки в подсолнухе располагаются по золотой спирали, точно так же, как и многие галактики, в том числе и галактика Солнечной системы. В гидротехнике по золотой спирали изгибают трубу, подводящую поток воды к лопастям турбины. Благодаря этому напор воды используется с наибольшей производительностью.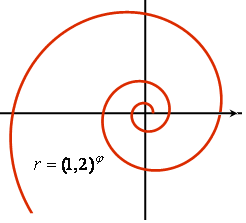
Можно сказать, что золотая спираль является математическим символом идеального соотношения формы и роста. Великий немецкий поэт Гёте считал ее даже математическим символом жизни и духовного развития.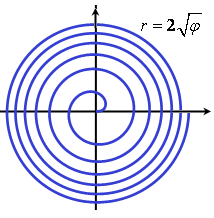
Спираль Ферма: 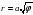 . Любопытное отличие спирали Ферма от других спиралей заключается в том, что расстояние между ее витками неограниченно убывает по мере удаления от полюса.
. Любопытное отличие спирали Ферма от других спиралей заключается в том, что расстояние между ее витками неограниченно убывает по мере удаления от полюса.
Гиперболическая спираль: 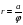 . По мере роста
. По мере роста 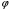 спираль устремляется к полюсу, делая вокруг него бесконечное множество витков, расстояние между которыми убывает.
спираль устремляется к полюсу, делая вокруг него бесконечное множество витков, расстояние между которыми убывает.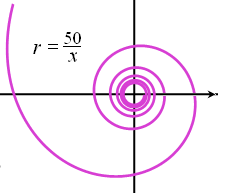
Спираль Галилея: 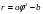 ,
, 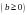 . Спираль Галилея вошла в историю математики в 17 столетии в связи с постановкой проблемы определения формы линии, по которой должна двигаться свободно падающая в области экватора точка, если бы она не обладала начальной скоростью, сообщаемой ей вращением земного шара.
. Спираль Галилея вошла в историю математики в 17 столетии в связи с постановкой проблемы определения формы линии, по которой должна двигаться свободно падающая в области экватора точка, если бы она не обладала начальной скоростью, сообщаемой ей вращением земного шара.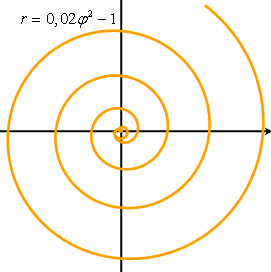
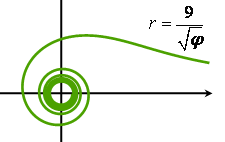
Спираль «жезл»: 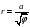 . Еще одна спираль. По форме напоминает жезл египетских фараонов.
. Еще одна спираль. По форме напоминает жезл египетских фараонов.
3






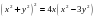
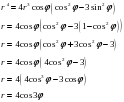
 . Для того, чтобы построить эту кривую наиболее точно, с малым шагом изменения угла F, как мы это делали при построении тригонометрических функций, мы выберем шаг изменения 0,1.
. Для того, чтобы построить эту кривую наиболее точно, с малым шагом изменения угла F, как мы это делали при построении тригонометрических функций, мы выберем шаг изменения 0,1. 
 .
. 

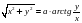 , в полярных координатах:
, в полярных координатах: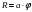 , где а - коэффициент пропорциональности (получили прямо-пропорциональную зависимость). Расстояния между соседними витками спирали есть величина постоянная и равна - а. Различают правую и левую спираль, закрученную по- или против- часовой стрелки.
, где а - коэффициент пропорциональности (получили прямо-пропорциональную зависимость). Расстояния между соседними витками спирали есть величина постоянная и равна - а. Различают правую и левую спираль, закрученную по- или против- часовой стрелки.
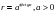 .
. 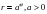 (частный случай логарифмической спирали). Эту кривую можно заметить в созданиях природы. Например, раковины многих моллюсков, улиток, рога архаров закручиваются по золотой спирали. Один из наиболее распространенных пауков, эпейра, сплетает свою паутину по золотой спирали. Cемечки в подсолнухе располагаются по золотой спирали, точно так же, как и многие галактики, в том числе и галактика Солнечной системы. В гидротехнике по золотой спирали изгибают трубу, подводящую поток воды к лопастям турбины. Благодаря этому напор воды используется с наибольшей производительностью.
(частный случай логарифмической спирали). Эту кривую можно заметить в созданиях природы. Например, раковины многих моллюсков, улиток, рога архаров закручиваются по золотой спирали. Один из наиболее распространенных пауков, эпейра, сплетает свою паутину по золотой спирали. Cемечки в подсолнухе располагаются по золотой спирали, точно так же, как и многие галактики, в том числе и галактика Солнечной системы. В гидротехнике по золотой спирали изгибают трубу, подводящую поток воды к лопастям турбины. Благодаря этому напор воды используется с наибольшей производительностью.

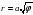 . Любопытное отличие спирали Ферма от других спиралей заключается в том, что расстояние между ее витками неограниченно убывает по мере удаления от полюса.
. Любопытное отличие спирали Ферма от других спиралей заключается в том, что расстояние между ее витками неограниченно убывает по мере удаления от полюса.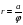 . По мере роста
. По мере роста 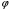 спираль устремляется к полюсу, делая вокруг него бесконечное множество витков, расстояние между которыми убывает.
спираль устремляется к полюсу, делая вокруг него бесконечное множество витков, расстояние между которыми убывает.
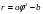 ,
, 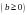 . Спираль Галилея вошла в историю математики в 17 столетии в связи с постановкой проблемы определения формы линии, по которой должна двигаться свободно падающая в области экватора точка, если бы она не обладала начальной скоростью, сообщаемой ей вращением земного шара.
. Спираль Галилея вошла в историю математики в 17 столетии в связи с постановкой проблемы определения формы линии, по которой должна двигаться свободно падающая в области экватора точка, если бы она не обладала начальной скоростью, сообщаемой ей вращением земного шара.

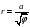 . Еще одна спираль. По форме напоминает жезл египетских фараонов.
. Еще одна спираль. По форме напоминает жезл египетских фараонов.









