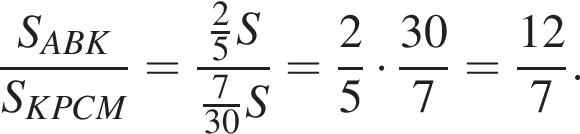Вариант № 10
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырех цифр без пробелов, запятых и других дополнительных символов.
| Объекты | коридор | кладовая | спальня | кухня |
| Цифры |
|
|
|
|

На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка.
Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора — дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пройти на одну из застеклённых лоджий. Самое большое по площади помещение — гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию.
Решение. Вход в квартиру находится в коридоре, следовательно, он отмечен на плане цифрой 2, слева от входа в гостиную комнату отмечен санузел под цифрой 1, в противоположном конце под цифрой 3 отмечена кладовая. Из кладовой можно пройти в спальню, отмеченную цифрой 4, а из нее в лоджию, которая отмечена на плане цифрой 5. Гостиная, как самое большое помещение, отмечена цифрой 6, кухня — цифрой 7 и еще одна лоджия под цифрой 8.
Ответ: 2347.
2. Плитка для пола размером 40 см на 40 см продаётся в упаковках по 12 штук. Сколько упаковок плитки понадобится, чтобы выложить пол санузла?
Решение. Пол санузла является прямоугольником со сторонами 2 м и 2,4 м. Укладывая плитки в шесть рядов по 5 штук в ряду, пол можно замостить полностью. Таким образом, понадобится 30 плиток, то есть 3 упаковки.
Ответ: 3.
3. Найдите площадь меньшей лоджии. Ответ дайте в квадратных метрах.
Решение. Меньшая лоджия является прямоугольником со сторонами 3 и 10 клеток, если длина клетки равна 0,4 м, то площадь лоджии составляет 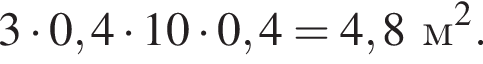
Ответ: 4,8.
4. На сколько процентов площадь кухни больше площади кладовой?
Решение. Кухня обозначена на плане цифрой 7. Её площадь 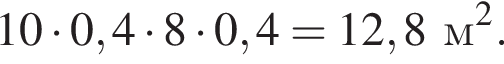 Кладовая обозначена на плане цифрой 3. Её площадь
Кладовая обозначена на плане цифрой 3. Её площадь 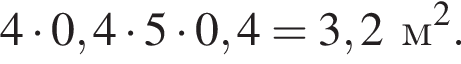 Таким образом, площадь кухни больше площади кладовой на
Таким образом, площадь кухни больше площади кладовой на 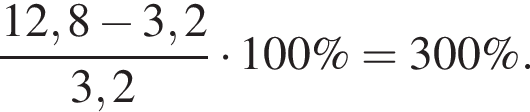
Ответ: 300.
5. В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с фронтальной загрузкой вместимостью не менее 6 кг.
| Модель | Вместимость барабана (кг) | Тип загрузки | Стоимость (руб.) | Стоимость подключения (руб.) | Стоимость доставки (% от стоимости машины) | Габариты (высота × ширина × глубина, см) |
| А | 7 | верт. | 28 000 | 1700 | бесплатно | 85 × 60 × 45 |
| Б | 5 | фронт. | 24 000 | 4500 | 10 | 85 × 60 × 40 |
| В | 5 | фронт. | 25 000 | 5000 | 10 | 85 × 60 × 40 |
| Г | 6,5 | фронт. | 24 000 | 4500 | 10 | 85 × 60 × 44 |
| Д | 6 | фронт. | 28 000 | 1700 | бесплатно | 85 × 60 × 45 |
| Е | 6 | верт. | 27 600 | 2300 | бесплатно | 89 × 60 × 40 |
| Ж | 6 | верт. | 27 585 | 1900 | 10 | 89 × 60 × 40 |
| З | 6 | фронт. | 20 000 | 6300 | 15 | 85 × 60 × 42 |
| И | 5 | фронт. | 27 000 | 1800 | бесплатно | 85 × 60 × 40 |
| К | 5 | верт. | 27 000 | 1800 | бесплатно | 85 × 60 × 40 |
Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?
Решение. Наиболее дешевый подходящий вариант — модель З, ее стоимость вместе с подключением и доставкой составит 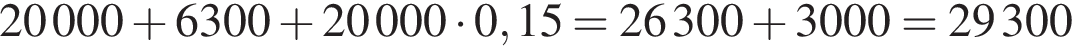 руб.
руб.
Ответ: 29 300.
6. Найдите значение выражения 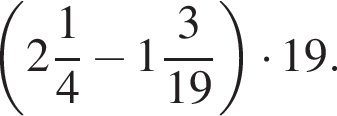
Решение. Раскроем скобки:
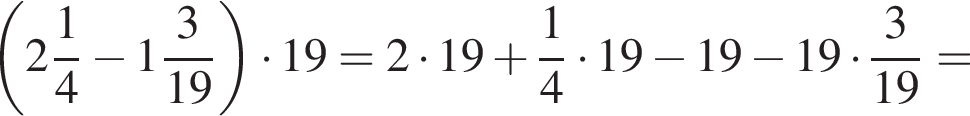
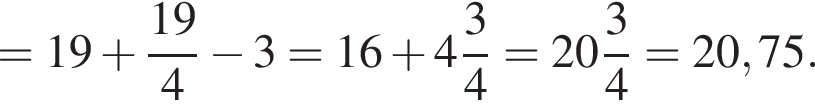
Ответ: 20,75.
7. Значение какого из данных выражений положительно, если известно, что 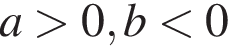
1)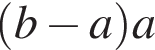
2)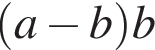
3)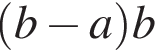
4)ab
Решение. Заметим, что 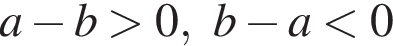 . Имеем:
. Имеем:
1)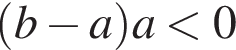
2)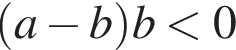
3)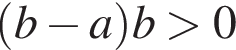
4)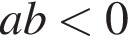
Ответ: 3
8. Найдите значение выражения 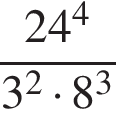 .
.
Решение. Вычислим:
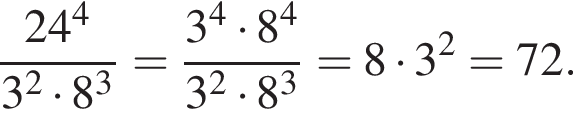
Ответ: 72.
9. Найдите корни уравнения 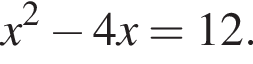
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение. Перенесём всё в уравнении в одну сторону:
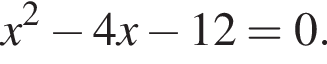
По теореме, обратной теореме Виета, сумма корней равна 4, а их произведение равно −12. Тем самым, это числа −2 и 6.
Ответ: −26.
10. Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.
Решение. Всего трехзначных чисел 900. На пять делится каждое пятое из них, то есть таких чисел 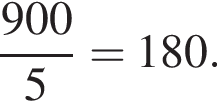 Вероятность того, что Коля выбрал трехзначное число, делящееся на 5, определяется отношением количества трехзначных чисел, делящихся на 5, ко всему количеству трехзначных чисел:
Вероятность того, что Коля выбрал трехзначное число, делящееся на 5, определяется отношением количества трехзначных чисел, делящихся на 5, ко всему количеству трехзначных чисел: 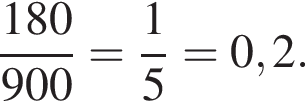
Ответ: 0,2.
Примечание.
Количества чисел можно было не находить: искомая вероятность равна одной пятой потому, что пятая часть чисел делится на 5.
Приведем решение с нахождением количества чисел, делящихся на 5.
Трехзначные числа - это числа от 100 до 999, всего их 900.
Найдем первое число в заданном диапазоне, делящееся на 5 — это 100 = 5 · 20.
Найдем первое число, большее правой границы диапазона, делящееся на 5 — это 1000 = 5 · 200.
Тогда количество чисел, делящихся на 5, в заданном диапазоне равно 200 − 20 = 180.
Вероятность выбрать трехзначное число, делящееся на 5, равна 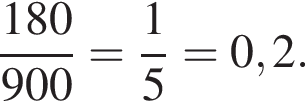
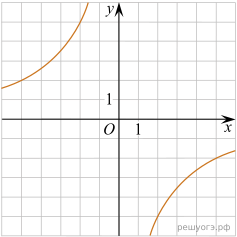
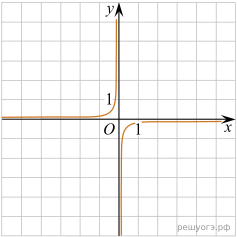
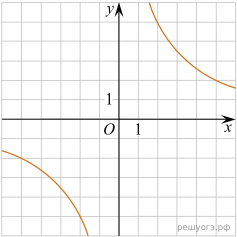
11. Установите соответствие между графиками функций и формулами, которые их задают.
Графики
Коэффициенты
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Решение. Все представленные здесь функции — гиперболы. Общая формула для уравнения гиперболы: 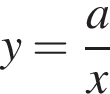 , если
, если  , то ветви гиперболы располагаются в первой и третьей четвертях, в противном случае — во второй и четвёртой четвертях.
, то ветви гиперболы располагаются в первой и третьей четвертях, в противном случае — во второй и четвёртой четвертях.
Для того, чтобы отличить гиперболы лежащие в одинаковых четвертях нужно подставить какое-нибудь значение x в формулу и проверить, какому графику будет соответствовать полученное значение.
Таким образом, установим соответсвие: А — 2, Б — 3, В — 4.
Ответ: 234.
12. Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 180 ватт, а сила тока равна 6 амперам.
Решение. Выразим сопротивление из формулы для мощности: 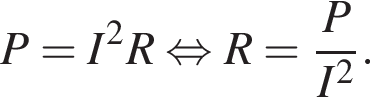
Подставляя, получаем:
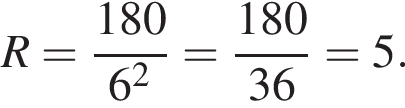
Ответ: 5.
13. Укажите решение неравенства 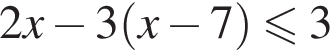
1)
2)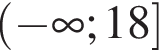
3)
4)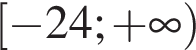
Решение. Последовательно получаем:

Правильный ответ указан под номером: 3.
Ответ: 3
14. Ире надо подписать 880 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Ира подписала 10 открыток. Определите, сколько открыток было подписано за восьмой день, если вся работа была выполнена за 16 дней.
Решение. В первый день Ира подписала  открыток, во второй —
открыток, во второй — 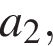 …, в последний —
…, в последний — 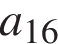 открыток. Всего было подписано
открыток. Всего было подписано 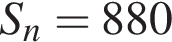 открыток. Если количество подписываемых открыток увеличивалось на d каждый день, то
открыток. Если количество подписываемых открыток увеличивалось на d каждый день, то
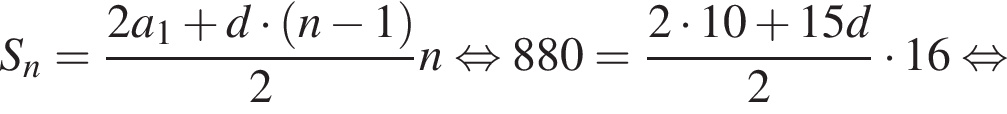

Тогда
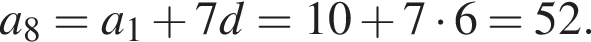
Следовательно, за восьмой день было подписано 52 открытки.
Ответ: 52.
15.
В треугольнике ABC известно, что  , AD - биссектриса. Найдите угол BAD. Ответ дайте в градусах.
, AD - биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Решение. Поскольку AD - биссектриса, то 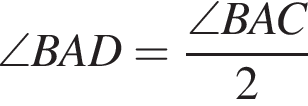 . Таким образом,
. Таким образом, 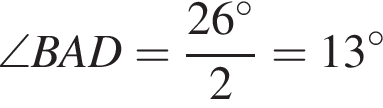
Ответ: 13
16.
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 75°. Найдите величину угла OMK. Ответ дайте в градусах.
Решение. Угол, образованный хордой и касательной равен половине дуги, которую он заключает, поэтому величина дуги MK равна 2 · 75° = 150°. Угол MOK — центральный, поэтому он равен величине дуги, на которую опирается. Значит, угол MOK равен 150°. В треугольнике OMK стороны OK и OM равны как радиусы окружности, поэтому треугольник OMK — равнобедренный, следовательно, углы при основании равны. Сумма углов треугольника равна 180°, поэтому ∠OKM = ∠OMK = (180° − ∠KOM)/2 = (180° − 150°)/2 = 15°.
Ответ: 15.
17.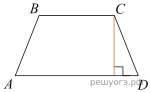
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
Решение. 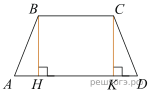 Проведём вторую высоту и введём обозначения, как показано на рисунке. Рассмотрим треугольники ABH и CKD, они прямоугольные, AB равно CD, BH равно CK, следовательно, эти треугольники равны, откуда
Проведём вторую высоту и введём обозначения, как показано на рисунке. Рассмотрим треугольники ABH и CKD, они прямоугольные, AB равно CD, BH равно CK, следовательно, эти треугольники равны, откуда  Найдём отрезок
Найдём отрезок 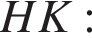
 Высоты BH и CK перпендикулярны AD, значит, они параллельны, BH равно CK, следовательно, HBCK — прямоугольник, поэтому
Высоты BH и CK перпендикулярны AD, значит, они параллельны, BH равно CK, следовательно, HBCK — прямоугольник, поэтому 
Ответ: 4.
18.
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.
Решение. 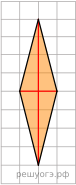 Площадь ромба равна половине произведения диагоналей, следовательно, равна 8.
Площадь ромба равна половине произведения диагоналей, следовательно, равна 8.
Ответ: 8.
19. Укажите номера верных утверждений.
1) Если один из углов треугольника прямой, то треугольник прямоугольный.
2) Диагонали квадрата точкой пересечения делятся пополам.
3) Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Решение. Проверим каждое из утверждений.
1) «Если один из углов треугольника прямой, то треугольник прямоугольный» — верно, по определению прямоугольного треугольника.
2) « Диагонали квадрата точкой пересечения делятся пополам» — верно, т. к. квадрат — частный случай параллелограмма.
3) «Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку» — верно по свойству серединного перпендикуляра.
Ответ: 123.
20. Решите уравнение 
Решение. Преобразуем уравнение:
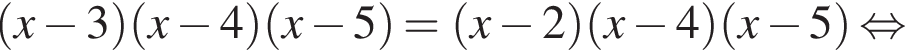
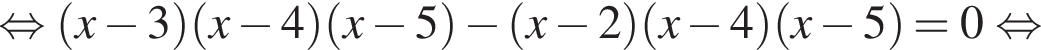
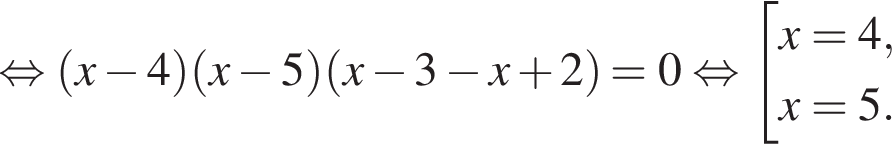
Ответ: 4; 5.
21. Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12 вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?
Решение. Пусть натуральное число x — количество вопросов теста. Тогда время, затраченное на выполнение теста Димой, составляет 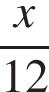 часа, а время, затраченное Сашей, составляет
часа, а время, затраченное Сашей, составляет 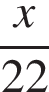 часа. Для решения теста Диме требуется на 75 минут или
часа. Для решения теста Диме требуется на 75 минут или  часа больше. Можно составить уравнение:
часа больше. Можно составить уравнение:
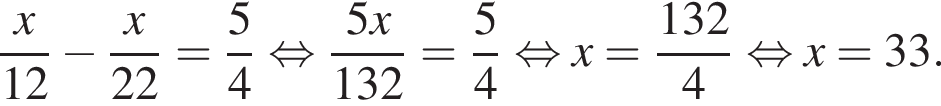
Следовательно, тест содержит 33 вопроса.
Ответ: 33.
22. Постройте график функции 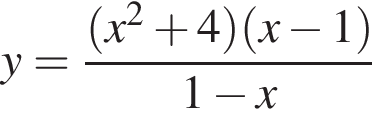 и определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.
Решение. Преобразуем выражение: 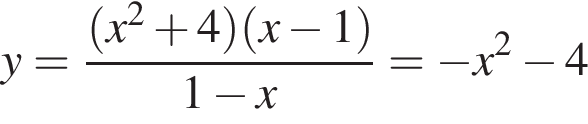 при условии, что
при условии, что 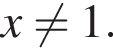
Построим график:
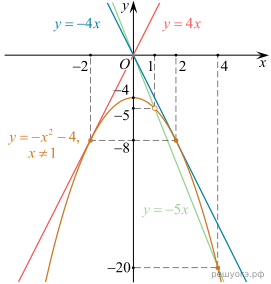
Прямая y = kx имеет с графиком ровно одну общую точку, если она проходит через точку (1; −5) или если уравнение 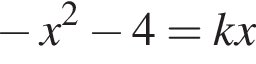 имеет один корень. Дискриминант уравнения
имеет один корень. Дискриминант уравнения 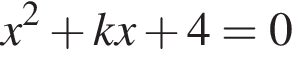 равен
равен  , и он должен быть равен нулю. Получаем, что k = −5, k = −4 и k = 4.
, и он должен быть равен нулю. Получаем, что k = −5, k = −4 и k = 4.
Ответ: -5; -4; 4.
23. Высота AH ромба ABCD делит сторону CD на отрезки DH = 15 и CH = 2. Найдите высоту ромба.
Решение. 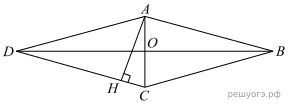 Введём обозначения, как показано на рисунке. Угол ODC и CAH равны как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники COD и ACH, они прямоугольные, углы ODC и CAH равны, следовательно, эти треугольники подобны, откуда
Введём обозначения, как показано на рисунке. Угол ODC и CAH равны как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники COD и ACH, они прямоугольные, углы ODC и CAH равны, следовательно, эти треугольники подобны, откуда 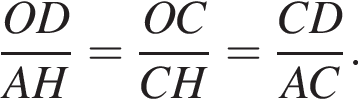 Диагонали ромба делятся точкой пересечения пополам:
Диагонали ромба делятся точкой пересечения пополам: 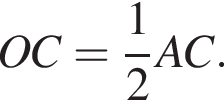 Получаем:
Получаем:

Из прямоугольного треугольника ACH, используя теорему Пифагора найдём 
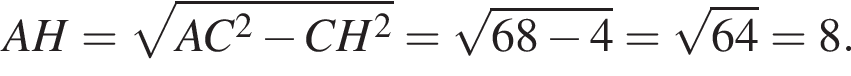
Ответ: 8.
-----------
Приведем другое решение:
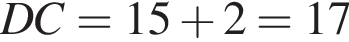
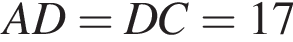
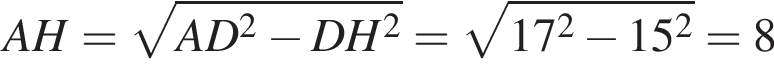
24. 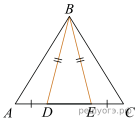 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рис.). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рис.). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
Решение. Так как по условию  то треугольник BDE является равнобедренным. Пусть угол при основании этого треугольника равен x, тогда
то треугольник BDE является равнобедренным. Пусть угол при основании этого треугольника равен x, тогда  Треугольники BEC и BDA равны по двум сторонам и углу между ними, поэтому
Треугольники BEC и BDA равны по двум сторонам и углу между ними, поэтому  и треугольник ABC —равнобедренный.
и треугольник ABC —равнобедренный.
25. В треугольнике ABC на его медиане BM отмечена точка K так, что BK : KM = 4 : 1. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Решение.  Пусть площадь треугольника ABC равна
Пусть площадь треугольника ABC равна 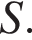 Медиана делит треугольник на два равновеликих треугольника, значит,
Медиана делит треугольник на два равновеликих треугольника, значит, 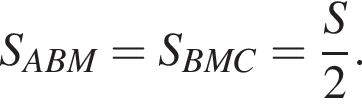 У треугольников ABK и ABM высота, проведенная к стороне BM, общая, поэтому площади этих треугольников относятся как их основания BK и BM, откуда:
У треугольников ABK и ABM высота, проведенная к стороне BM, общая, поэтому площади этих треугольников относятся как их основания BK и BM, откуда:
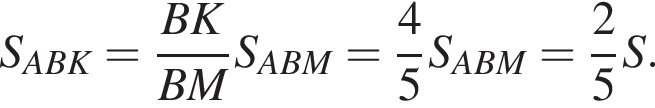
Проведём прямую MN, параллельную  Точка M — середина AC, следовательно, MN — средняя линия треугольникаAPC, значит,
Точка M — середина AC, следовательно, MN — средняя линия треугольникаAPC, значит,  По теореме Фалеса для угла MBC находим:
По теореме Фалеса для угла MBC находим: 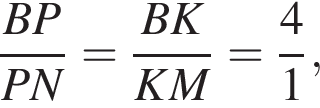 а так как
а так как 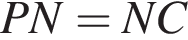 получаем, что
получаем, что 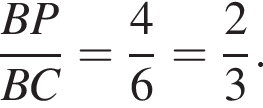
Стороны треугольников BKP и BMC сонаправлены, их площади относятся как произведение отношений сонаправленных сторон, поэтому
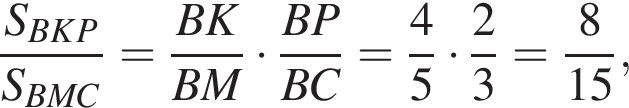
то есть 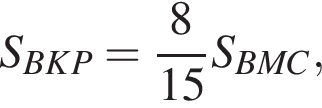 откуда
откуда 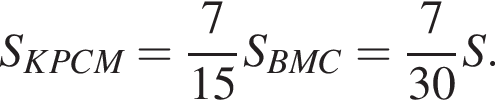
Тем самым, для искомого отношения площадей имеем:
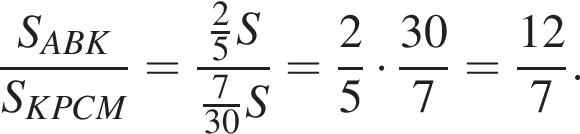
Ответ: 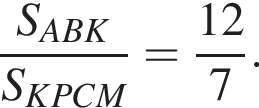
| № задания | ответ |
| 1 | 2347 |
| 2 | 3 |
| 3 | 4,8 |
| 4 | 300 |
| 5 | 29 300 |
| 6 | 20,75 |
| 7 | 3 |
| 8 | 72 |
| 9 | -26 |
| 10 | 0,2 |
| 11 | 234 |
| 12 | 5 |
| 13 | 3 |
| 14 | 52 |
| 15 | 13 |
| 16 | 15 |
| 17 | 4 |
| 18 | 8 |
| 19 | 123 |
| 20 | 4; 5 |
| 21 | 33 |
| 22 | -5; -4; 4 |
| 23 | 8 |
| 24 | - |
| 25 | 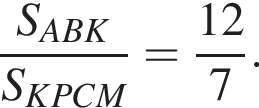
|











 Проведём вторую высоту и введём обозначения, как показано на рисунке. Рассмотрим треугольники ABH и CKD, они прямоугольные, AB равно CD, BH равно CK, следовательно, эти треугольники равны, откуда
Проведём вторую высоту и введём обозначения, как показано на рисунке. Рассмотрим треугольники ABH и CKD, они прямоугольные, AB равно CD, BH равно CK, следовательно, эти треугольники равны, откуда 
 Площадь ромба равна половине произведения диагоналей, следовательно, равна 8.
Площадь ромба равна половине произведения диагоналей, следовательно, равна 8.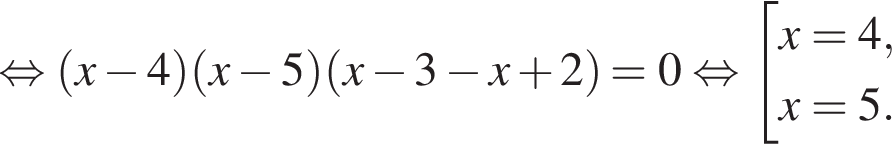

 Введём обозначения, как показано на рисунке. Угол ODC и CAH равны как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники COD и ACH, они прямоугольные, углы ODC и CAH равны, следовательно, эти треугольники подобны, откуда
Введём обозначения, как показано на рисунке. Угол ODC и CAH равны как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники COD и ACH, они прямоугольные, углы ODC и CAH равны, следовательно, эти треугольники подобны, откуда 
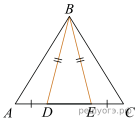 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рис.). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рис.). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный. Пусть площадь треугольника ABC равна
Пусть площадь треугольника ABC равна