20_1 задание. Программы для робота.

20_1 Робот. Общие сведения.

Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может. У Робота есть девять команд. Четыре команды – это команды-приказы:вверх вниз влево вправо

При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится.Также у Робота есть команда закрасить, при которой закрашивается клетка, где находится Робот в настоящий момент. Ещё четыре команды – это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:

сверху свободно снизу свободно слева свободно справа свободно

Эти команды можно использовать вместе с условием «eсли», имеющим следующий вид:

если условие то

последовательность команд

все

Здесь условие – одна из команд проверки условия.

Последовательность команд – это одна или несколько любых команд-приказов. Например, для передвижения на одну клетку вправо, если справа нет стенки, и закрашивания клетки, можно использовать такой алгоритм:

если справа свободно то

вправо

закрасить

все

В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не, например:

если (справа свободно) и (не снизу свободно) то

вправо

все

Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:

нц пока условие

последовательность команд

кц

Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:

нц пока справа свободно

вправо

кц

1. На бесконечном поле имеются две одинаковые вертикальные стены и одна горизонтальная, соединяющая верхние концы стен. Длины стен неизвестны. Робот находится в одной из клеток, расположенных между нижними краями вертикальных стен. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).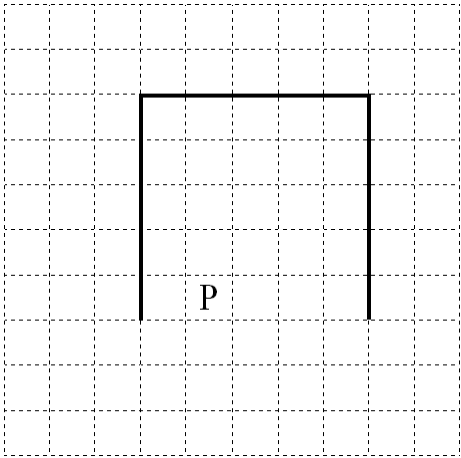

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные выше горизонтальной стены непосредственно над ней. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля.

При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.

1. На бесконечном поле имеются две одинаковые вертикальные стены и одна горизонтальная, соединяющая нижние концы стен. Длины стен неизвестны. Робот находится в одной из клеток, расположенных между верхними краями вертикальных стен. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные ниже горизонтальной стены непосредственно под ней. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).Конечное расположение Робота может быть произвольным.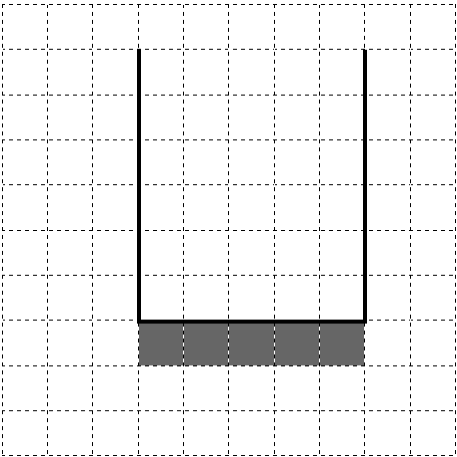

Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.

1. На бесконечном поле имеется лестница. Сначала лестница слева направо спускается вниз, затем поднимается вверх. Высота каждой ступени – одна клетка, ширина – две клетки. Робот находится на первой ступеньке лестницы, в левой клетке. Количество ступеней, ведущих вниз, и количество ступеней, ведущих вверх, неизвестно.

На рисунке указан один из возможных способов расположения лестницы и Робота (Робот обозначен буквой «Р»).

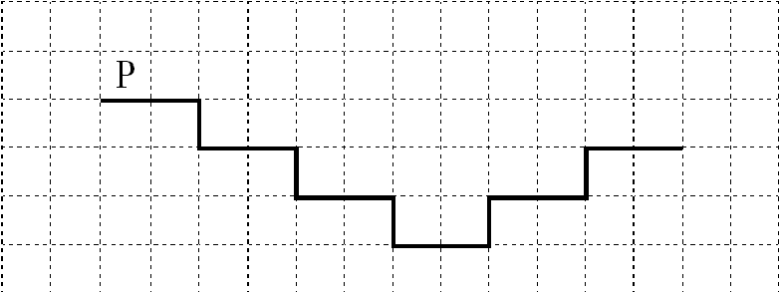
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно над ступенями лестницы. Требуется закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).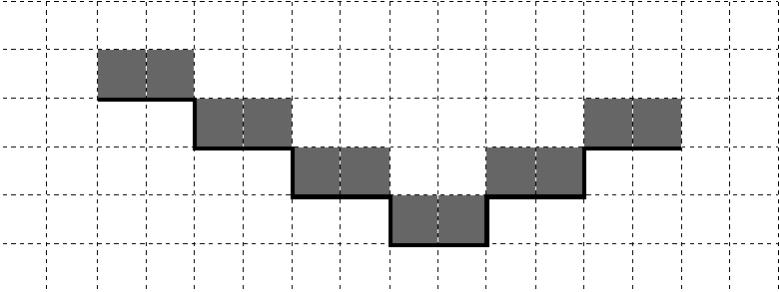

Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения ступеней внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.

1. На бесконечном поле имеется лестница. Сначала лестница спускается вниз (справа налево), затем поднимается вверх. Высота каждой ступени – одна клетка, ширина – две клетки. Робот находится под верхней ступенькой правой части лестницы, в правой клетке. Количество ступенек, ведущих вниз, и количество ступенек, ведущих вверх, неизвестно. На рисунке указан один из возможных способов расположения лестницы и Робота (Робот обозначен буквой «Р»).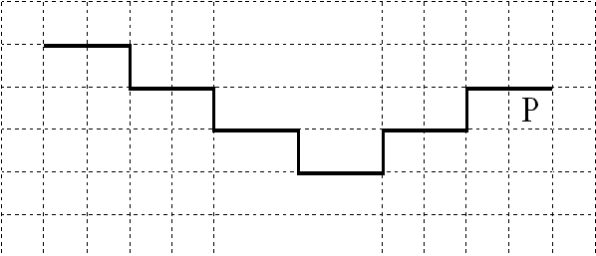

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно под ступенями лестницы. Требуется закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).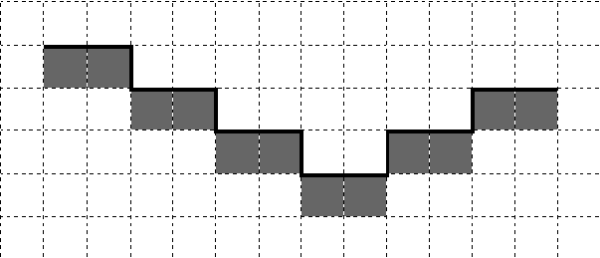

Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения ступеней внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.

1. На бесконечном поле имеется стена, длины отрезков стены неизвестны. Стена состоит из одного горизонтального и трёх равных вертикальных отрезков (отрезки стены расположены буквой «Ш»). Все отрезки неизвестной длины. Робот находится в клетке, расположенной непосредственно справа от верхнего конца левого вертикального отрезка. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р») .

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно справа от второго вертикального отрезка. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).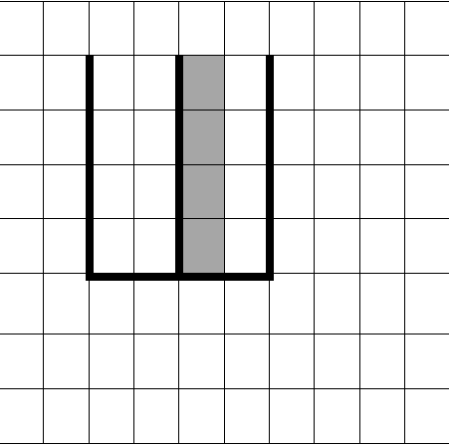

Конечное расположение Робота может быть произвольным. При исполнении алгоритма Робот не должен разрушиться. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен.

1. На бесконечном поле имеется длинная горизонтальная стена. Длина стены неизвестна. Робот находится в одной из клеток непосредственно сверху от стены. Начальное положение Робота также неизвестно. Одно из возможных положений Робота приведено на рисунке (Робот обозначен буквой «Р»):

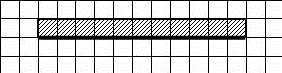
Напишите алгоритм для Робота, закрашивающий все клетки, расположенные выше стены и прилегающие к ней, независимо от размера стены и начального расположения Робота. Робот должен закрасить только клетки, удовлетворяющие заданному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки:

Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться.

1. На бесконечном поле имеется вертикальная стена. Длина стены неизвестна. От верхнего конца стены вправо отходит горизонтальная стена также неизвестной длины. От правого конца этой стены отходит вниз вторая вертикальная стена неизвестной длины. Робот находится в клетке, расположенной справа от нижнего края первой вертикальной стены. На рисунке указан один из возможных способов расположения стен и Робота(Робот обозначен буквой «Р»).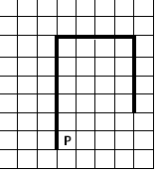

Напишите для Робота алгоритм, закрашивающий клетку, на которой находится Робот первоначально, и клетки, расположенные слева от второй вертикальной стены. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).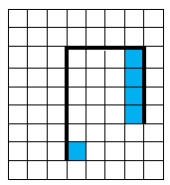

Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться.