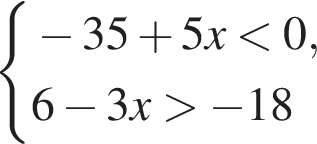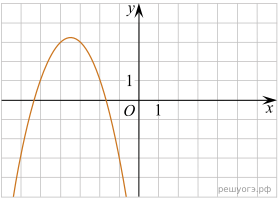© 2024, Максимов Олег Анатольевич 722 7


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока


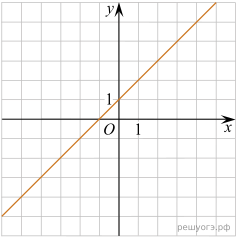
28 тренировочных вариантов ОГЭ 2024
28 тренировочных вариантов ОГЭ 2024. КИМ размещены для удобной печати на листах формата А4
Просмотр содержимого документа
«28 тренировочных вариантов ОГЭ 2024»
©2024 Составил учитель математики Максимов О.А. Подготовка к ОГЭ, ЕГЭ: maksoleg@mail.ru

ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 01, задачи 1-25
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырех цифр.
| Объекты | гостиная | кухня | ванная комната | кладовая комната |
| Цифры |
|
|
|
|

На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Квартира имеет прямоугольную форму. Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположен коридор, отмеченный цифрой 1, а справа находится кладовая комната, которая занимает площадь в 20 кв. м.
Гостиная занимает наибольшую площадь в квартире, а слева от нее находится кухня. Прямо перед гостиной находится детская.
В верхнем правом углу схемы находится санузел, отмеченный цифрой 6. Прямо напротив него располагается ванная комната.
В санузле и ванной комнате пол выложен плиткой, которая имеет размер 0,5 м × 0,5 м.
В квартире стоит однотарифный счетчик электроэнергии. Имеется возможность установить двухтарифный счетчик.
2. Плитка продается в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол в ванной комнате и санузле?
3. Найдите площадь, которую занимает гостиная. Ответ дайте в квадратных метрах.
4. Найдите расстояние от верхнего левого угла квартиры до нижнего правого угла квартиры (расстояние между двумя ближайшими точками по прямой) в метрах.
5. Хозяин квартиры планирует заменить в квартире счетчик. Он рассматривает два варианта: однотарифный или двухтарифный счетчики. Цены на оборудование и стоимость его установки, данные о тарифах оплаты, и их стоимости даны в таблице.
|
| Оборудованиеи монтаж | Сред. потребл.мощность в час | Стоимость оплаты |
| Однотарифный | 5100 руб. | 3,5 кВт · ч | 2 руб./(кВт · ч ) |
| Двухтарифный | 10 000 руб. | 3,5 кВт · ч | 2 руб./(кВт · ч) днем |
| 1 руб./(кВт · ч ) ночью(с 23:00 до 6:00) |
Обдумав оба варианта, хозяин решил установить двухтарифный электросчетчик. Через сколько дней непрерывного использования электричества экономия от использования двухтарифного счетчика вместо однотарифного компенсирует разность в стоимости установки двухтарифного счетчика и однотарифного?
6. Вычислите: ![]()
7. На координатной прямой точками отмечены числа ![]()
![]()
Какому числу соответствует точка А?
1)![]() ; 2)
; 2)![]() ; 3)
; 3)![]() ; 4)
; 4)![]()
8. Найдите значение выражения
![]() при
при ![]() и
и ![]()
9. Решите уравнение ![]()
10. У бабушки 20 чашек: 9 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
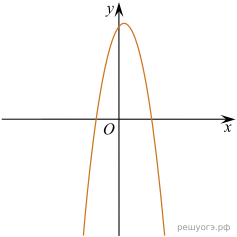
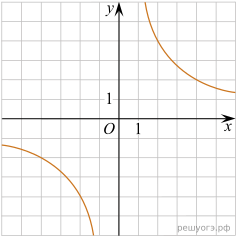
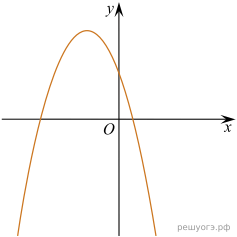
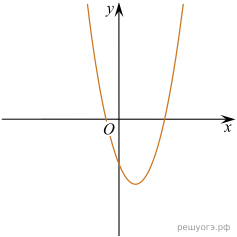
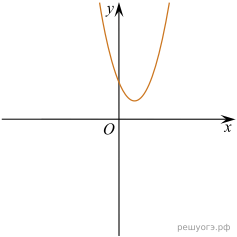
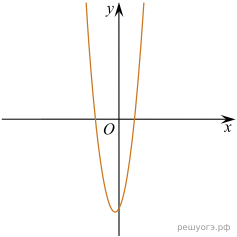
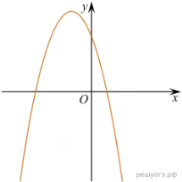
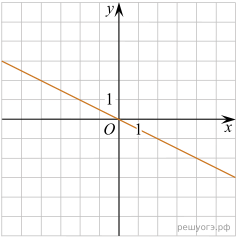
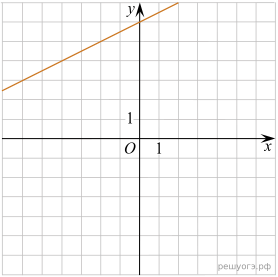
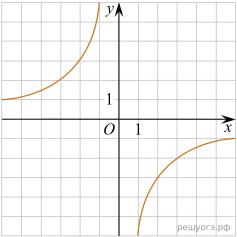
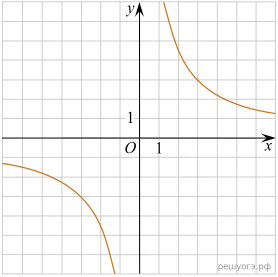
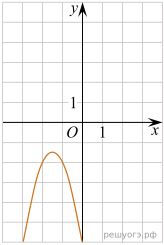
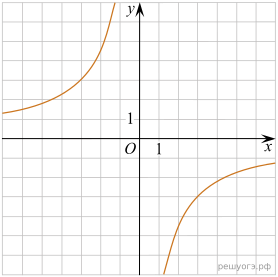
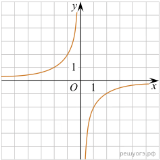
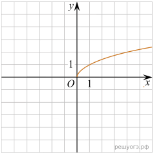
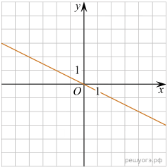
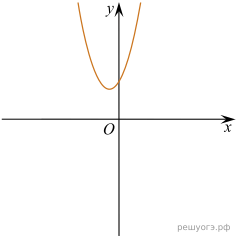
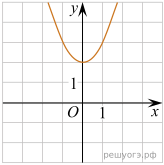
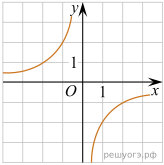
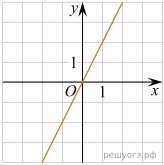
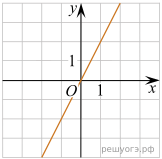
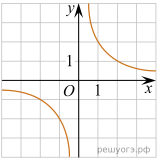
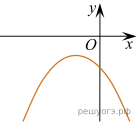
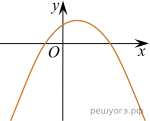
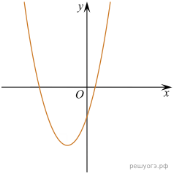
11. На рисунках изображены графики функций вида ![]() Установите соответствие между знаками коэффициентов k и b и графиками функций.
Установите соответствие между знаками коэффициентов k и b и графиками функций.
А) ![]() Б)
Б) ![]() В)
В) ![]()
| А | Б | В |
|
|
|
|
12. В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле ![]() где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 9 колец. Ответ дайте в рублях.
где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 9 колец. Ответ дайте в рублях.
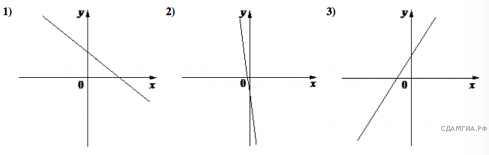
13. Укажите решение системы неравенств
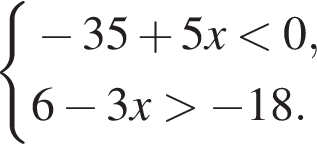
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
14. В амфитеатре 12 рядов. В первом ряду 18 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
15. В прямоугольном треугольнике ABC катет AC = 50, а высота CH, опущенная на гипотенузу, равна 48. Найдите ![]()
![]()

16. На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

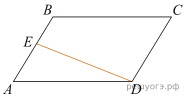
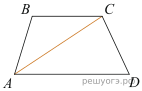
17. Площадь параллелограмма ABCD равна 7. Точка E — середина стороны AB. Найдите площадь трапеции EBCD.
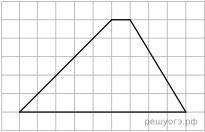
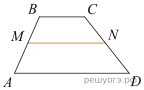
18. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину ее средней линии.
19. Какое из следующих утверждений верно?
1) Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти окружности касаются.
2) Вписанные углы окружности равны.
3) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.
4) Через любые четыре точки, не принадлежащие одной прямой, проходит единственная окружность.
20. Найдите значение выражения
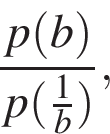 если
если ![]()
21. Свежие фрукты содержат 86 % воды, а высушенные — 23 %. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов?
22. Известно, что графики функций
![]() и
и ![]() имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
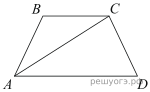
23. Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD = 40.
24. В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKB.
25. Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 36, тангенс угла BAC равен ![]() Найдите радиус окружности, вписанной в треугольник ABC.
Найдите радиус окружности, вписанной в треугольник ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 01, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 02, задачи 1-25
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырех цифр.
| Объекты | Гостиная | Баня | Гараж | Кухня |
| Цифры |
|
|
|
|
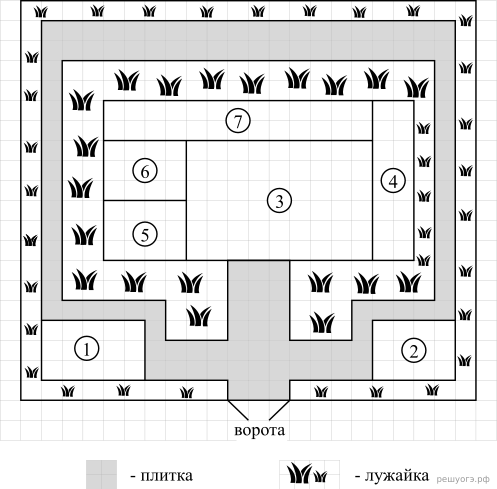
Инна Сергеевна имеет дом с участком. На рисунке приведен план этого участка.
При входе на участок слева находится гараж площадью 15 м2, справа расположена баня. Дом находится внутри участка, имеет форму прямоугольника. Сторона каждой клетки на плане равна 1 метру.
Вход в дом осуществляется через стеклянную дверь. Внутри дома расположены: кухня, гостиная, спальня, детская комната, подсобные помещения.
В центре дома находится гостиная, справа — кухня. Спальня и детская имеют равные площади, подсобные помещения обозначены на плане цифрой 7.
Площадка около входа и дорожки вокруг дома выложены плитками размером 1 м × 1 м, на остальной территории посеяна трава.
2. Тротуарная плитка продается в упаковках по 4 штуки. Сколько упаковок понадобилось купить, чтобы выложить все дорожки участка и площадку около входа?
3. Найдите площадь (в м2), которую занимает жилой дом.
4. Найдите расстояние от гаража до бани (расстояние между двумя ближайшими точками по прямой) в метрах.
5. Инна Сергеевна планирует произвести оклейку стен помещений: детской комнаты и спальни — обоями. Она рассмотрела два варианта: флизелиновые и текстильные обои. Данные о стоимости рулона, площади комнат, расходе обоев на комнаты представлены в таблице. Обдумав оба варианта, Инна Сергеевна решила наклеить текстильные обои. На сколько рублей выгоднее наклеить текстильные обои, чем флизелиновые?
| Тип обоев | Стоимость 1рулона (руб.) | Площадь стенкомнат (м2) | Расход обоевна 2 комнаты(рулоны) | Стоимость работпо поклейке обоев(руб.) |
| Флизелиновые | 1800 | 70 | 7 | 12 000 |
| Текстильные | 2100 | 70 | 5 | 12 500 |
6. Найдите значение выражения ![]()
7. На координатной прямой отмечены числа x и y:
![]()
Какое из следующих утверждений неверно?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
8. Найдите значение выражения ![]() при
при ![]()
9. Уравнение ![]() имеет корни −6; 4. Найдите
имеет корни −6; 4. Найдите ![]()
10. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
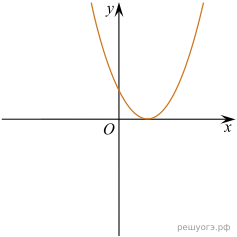
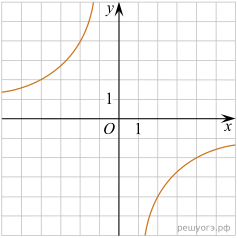
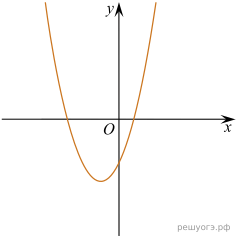
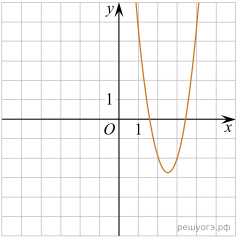
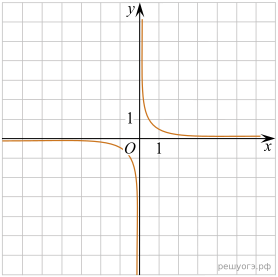
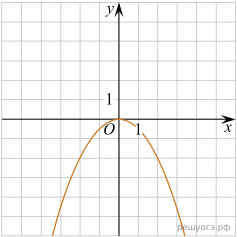
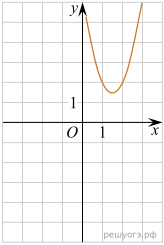
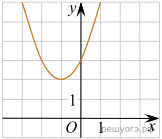
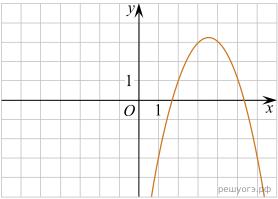
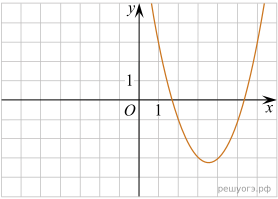
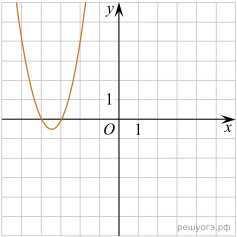
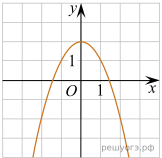
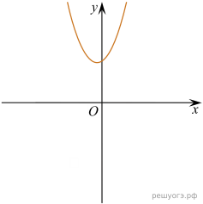
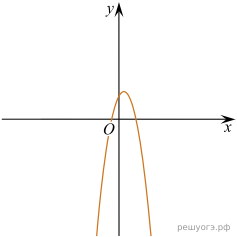
11. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) ![]() Б)
Б) ![]() В)
В) ![]()
| 1)
| 2)
| 3)
|
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В |
|
|
|
|
12. Площадь треугольника можно вычислить по формуле ![]() где
где ![]() — длины сторон треугольника, r — радиус вписанной окружности. Вычислите длину стороны c, если
— длины сторон треугольника, r — радиус вписанной окружности. Вычислите длину стороны c, если ![]()
13. Решите неравенство ![]()
1) ![]() 2)
2) ![]()
3) ![]() 4) нет решений
4) нет решений
14. Хозяин договорился с рабочими, что они копают колодец на следующих условиях: за первый метр он заплатит им 3500 рублей, а за каждый следующий метр — на 1600 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 9 метров?
15. Сторона ромба равна 24, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Перечислите эти длины в ответе без пробелов в порядке неубывания

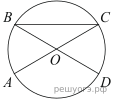
16. На окружности с центром O отмечены точки A и B так, что ![]() Длина меньшей дуги AB равна 58. Найдите длину большей дуги.
Длина меньшей дуги AB равна 58. Найдите длину большей дуги. 
17. Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB. 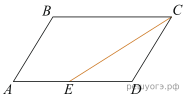
18. На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите длину его большей диагонали.

19. Какие из следующих утверждений верны?
1. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
2. Любой прямоугольник можно вписать в окружность.
3. Через заданную точку плоскости можно провести только одну прямую.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
20. Решите уравнение
![]()
21. Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобилиста на 11 км/ч, а вторую половину пути проехал со скоростью 66 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 40 км/ч.
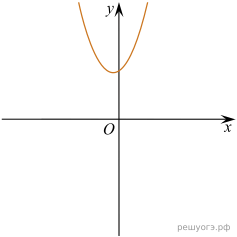
22. Постройте график функции ![]()
и определите, при каких значениях m прямая ![]() не имеет с графиком ни одной общей точки.
не имеет с графиком ни одной общей точки.
23. В прямоугольном треугольнике ABC с прямым углом C известны катеты:
![]()
![]() Найдите медиану CK этого треугольника.
Найдите медиану CK этого треугольника.
24. В треугольнике ABC с тупым углом BAC проведены высоты BB1 и CC1. Докажите, что треугольники AB1C1 и ABC подобны.
25. Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 96, тангенс угла BAC равен ![]() Найдите радиус окружности, вписанной в треугольник ABC.
Найдите радиус окружности, вписанной в треугольник ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 02, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 03, задачи 1-25
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырех цифр.
| Объекты | Пруд | Гараж | Будка | Теплица |
| Цифры |
|
|
|
|
На плане изображено домохозяйство по адресу: с. Малые Вершки, 1-й Советский пер., д. 6 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится гараж, а слева — баня, отмеченная на плане цифрой 6. Площадь, занятая баней, равна 9 кв. м.
Жилой дом находится в глубине территории. Помимо бани, жилого дома и гаража, на участке имеется будка, расположенная в углу участка, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Также в центре участка перед домом расположен пруд.
Все дорожки внутри участка вымощены тротуарной плиткой размером 0,5 м × 0,5 м. Между баней и гаражом имеется площадка, вымощенная такой же плиткой.
На участке планируется провести электричество.
2. Тротуарная плитка продается в упаковках по 7 штук. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед баней и гаражом?
3. Найдите площадь жилого дома (в м2).
4. Найдите длину окружности l пруда, если известно, что площадь пруда равна 2,25π м2. Ответ дайте в виде ![]()
5. Хозяин участка планирует провести на участок электричество. Он рассматривает два варианта: купить генератор или продлить до своего дома линию электропередач. Данные о расходе топлива (электроэнергии) и стоимости ценах указаны в таблице.
|
| Стоимость покупки(проведения) | Сред. расходтоплива /сред. расходэлектроэнергии | Стоимость топлива /электро-энергии |
| Генератор | 80 000 руб. | 2 л/ч | 45 руб./л |
| Линия электропередач | 60 000 руб. | 5 кВт | 20 руб./(кВт · ч ) |
Обдумав оба варианта, хозяин решил купить генератор. Через сколько часов непрерывного использования электроэнергии экономия от использования генератора вместо линии электропередач компенсирует разность в стоимости организации электричества на участке?
6. Найдите значение выражения ![]()
7. На координатной прямой точками отмечены числа
![]()

Какому числу соответствует точка B?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
8. Найдите значение выражения
![]() при
при ![]()
9. Найдите корни уравнения
![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. В магазине канцтоваров продается 264 ручки: 38 красных, 30 зеленых, 8 фиолетовых, остальные синие и черные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или черной.
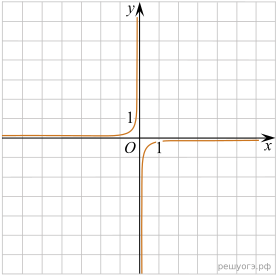
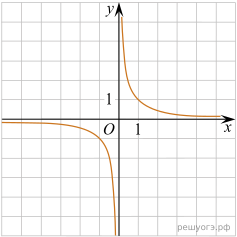
11. Установите соответствие между функциями и их графиками.
А)![]() Б)
Б)![]() В)
В)![]()
| 1)
| 2)
| 3)
|
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В |
|
|
|
|
12. Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле ![]() где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
13. Укажите решение неравенства
![]()
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
14. Бригада маляров красит забор длиной 810 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 180 метров забора. Определите, сколько дней бригада маляров красила весь забор.
15. Сторона квадрата равна ![]() Найдите диагональ этого квадрата.
Найдите диагональ этого квадрата.
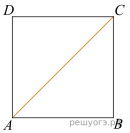
16. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 124°. Найдите величину угла BOC. Ответ дайте в градусах. 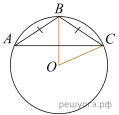
17. Высота BH ромба ABCD делит его сторону AD на отрезки ![]() и
и ![]() Найдите площадь ромба.
Найдите площадь ромба. 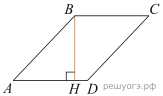
18. На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите длину его большей диагонали.

19. Какое из следующих утверждений верно?
1. Все квадраты имеют равные площади.
2. Основания равнобедренной трапеции равны.
3. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
В ответ запишите номер выбранного утверждения.
20. Решите уравнение ![]()
21. Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Через полчаса навстречу ему из В в А выехал велосипедист, который ехал со скоростью, на 11 км/ч большей скорости пешехода. Найдите скорость велосипедиста, если известно, что они встретились в 5 км от пункта А.
22. Постройте график функции
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
23. В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60° , сторона AB равна 4. Найдите площадь трапеции.
24. В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK = EN. Докажите, что данный параллелограмм — прямоугольник.
25. В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 03, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 04, задачи 1-25
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населенные пункты. В ответ запишите полученную последовательность четырех цифр.
| Насел. пункты | д. Лесная | п. Ковылкино | д. Николаевка | ст. Путянино |
| Цифры |
|
|
|
|
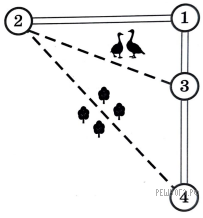
Аня летом отдыхает у дедушки и бабушки в деревне Николаевка. Аня с дедушкой собираются съездить на машине на железнодорожную станцию Путятино. Из Николаевки в Путятино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через поселок Ковылкино до деревни Лесная, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Путятино. Есть и третий маршрут: в Ковылкино можно свернуть на прямую грунтовую дорогу, которая идет мимо птицефабрики прямо в Путятино. По шоссе Аня с дедушкой едут со скоростью 72 км/ч, а по грунтовым дорогам — 50 км/ч. Расстояние по шоссе от Николаевки до Ковылкино равно 36 км, от Николаевки до Лесной — 60 км, а от Лесной до Путятино — 45 км.
2. На сколько процентов скорость, с которой едут Аня с дедушкой по шоссе, больше их скорости по грунтовой дороге?
3. Найдите расстояние от деревни Николаевка до Станции Путятино по прямой. Ответ дайте в километрах.
4. Сколько минут затратят на дорогу Аня с дедушкой, если поедут на станцию по прямой грунтовой дороге от Николаевки до Путятино?
5. На грунтовых дорогах машина дедушки расходует 9,2 литра бензина на 100 км. Известно, что на путь из Николаевки до Путятино через Ковылкино мимо птицефабрики и на путь через деревню Лесная ей необходим один и тот же объем бензина. Сколько литров бензина на 100 км машина дедушки расходует на шоссе?
6. Найдите значение выражения
![]()
7. Какое из данных ниже чисел принадлежит отрезку [8; 9]?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
8. Упростите выражение
![]() и найдите его значение при
и найдите его значение при ![]()
В ответ запишите полученное число.
9. Решите уравнение ![]()
10. У бабушки 10 чашек: 7 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
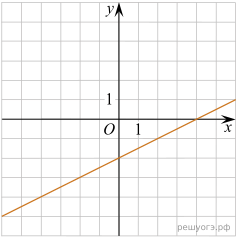
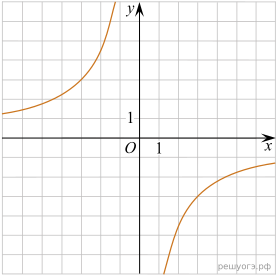
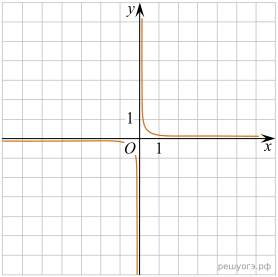
11. На рисунках изображены графики функций вида ![]() Установите соответствие между знаками коэффициентов k и b и графиками функций.
Установите соответствие между знаками коэффициентов k и b и графиками функций.
А) ![]() Б)
Б) ![]()
В) ![]()
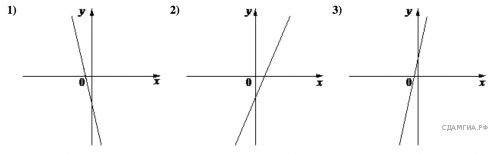
12. Центростремительное ускорение (в м/c2) вычисляется по формуле α = ω2R, где ω — угловая скорость (в с–1), R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 10 с–1, а центростремительное ускорение равно 54 м/c2.
13. Укажите решение системы неравенств:
|
|
|
14. Хозяин договорился с рабочими, что они копают колодец на следующих условиях: за первый метр он заплатит им 3500 рублей, а за каждый следующий метр — на 1600 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 9 метров?
15. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
16. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 24°. Ответ дайте в градусах.

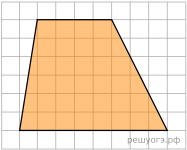
17. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите ее площадь. 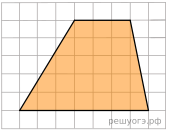
18. Площадь одной клетки равна 1. Найдите площадь закрашенной фигуры.

19. Какие из следующих утверждений верны?
1) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
2) Все диаметры окружности равны между собой.
3) Один из углов треугольника всегда не превышает 60 градусов.
Если вариантов ответов несколько, укажите их в порядке возрастания без пробелов и знаков препинания
20. Решите уравнение ![]()
21. Имеется два сплава с разным содержанием золота: в первом содержится 50%, а во втором — 80% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% золота?
22. Постройте график функции ![]()
Определите, при каких значениях m прямая ![]() имеет с графиком ровно три общие точки.
имеет с графиком ровно три общие точки.
23. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключенная внутри этого угла, равна 100°

24. Середины сторон параллелограмма являются вершинами ромба. Докажите, что данный параллелограмм — прямоугольник.
25. Диагонали четырехугольника ABCD, вершины которого расположены на окружности, пересекаются в точке M. Известно, что ![]() = 72°,
= 72°, ![]() = 102°,
= 102°, ![]() = 110°. Найдите
= 110°. Найдите ![]()
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 04, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 05, задачи 1-25
1. Для станций, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырех цифр.
| Станции | Пушкинская | Ладожская | Островская | Левобережная |
| Цифры |
|
|
|
|

На рисунке изображена схема метро города N. Станция Пушкинская расположена между станциями Беговая и Горная. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Горная, Ленинская, Красная, Островская, Новочеркасская. Синяя ветка включает в себя станции Беговая, Пушкинская, Горная, Красная и Ладожская. Петр живет недалеко от станции Левобережной, расположенной между станциями Новочеркасская и Петровская.
2. Бригада меняет рельсы на участке между станциями Левобережная и Петровская протяженностью 11,2 км. Работы начались в понедельник. Каждый рабочий день бригада меняла по 700 метров рельсов. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?
3. Территория, находящаяся внутри кольцевой линии, называется Приморским городским районом. Найдите его площадь S (в км2), если длина кольцевой ветки равна 60 км. В ответе укажите значение выражения S · π.
4. Найдите расстояние (в км) между станциями Горная и Красная, если длина Синей ветки равна 36 км, расстояние от Беговой до Красной равно 29 км, а от Ладожской до Горной — 23 км. Все расстояния даны по железной дороге.
5. Школьник Петр в среднем в месяц совершает 45 поездок в метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Петр уедет из города и неиспользованные карточки обнуляются. Во сколько рублей обойдется самый дешевый вариант?
| Количество поездок | Стоимость карточки(руб.) | Дополнительные условия |
| 1 | 20 | школьникам скидка 15% |
| 10 | 185 | школьникам скидка 10% |
| 30 | 525 | школьникам скидка 10% |
| 50 | 800 | нет |
| Не ограничено | 1000 | нет |
6. Найдите значение выражения
![]()
7. Известно, что число m отрицательное. На каком из рисунков точки с координатами ![]() расположены на координатной прямой в правильном порядке?
расположены на координатной прямой в правильном порядке?
| 1)
| 2)
|
| ||
|
| 3)
| 4)
| ||
В ответе укажите номер правильного варианта.
8. Найдите значение выражения
![]() при
при ![]()
9. Найдите корень уравнения
![]()
10. На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача по теме «Углы», равна 0,35. Вероятность того, что это окажется задача по теме «Окружность», равна 0,45. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
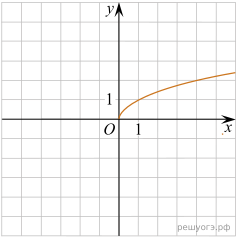
11. Найдите значение a по графику функции ![]() изображенному на рисунке.
изображенному на рисунке.
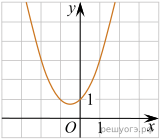
12. Расстояние s (в метрах) до места удара молнии можно приближенно вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 14 с. Ответ дайте в километрах, округлив его до целых.
13. Решите неравенство ![]() и определите, на каком рисунке изображено множество его решений.
и определите, на каком рисунке изображено множество его решений.
В ответе укажите номер правильного варианта.
|
|
|
|
|
|
14. Бригада маляров красит забор длиной 270 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 90 метров забора. Определите, сколько дней бригада маляров красила весь забор.
15. Катеты прямоугольного треугольника равны 4 и 3. Найдите синус наименьшего угла этого треугольника.

16. Касательные в точках A и B к окружности с центром O пересекаются под углом 88°. Найдите угол ABO. Ответ дайте в градусах.

17. Площадь прямоугольного треугольника равна ![]() Один из острых углов равен 30°. Найдите длину катета, прилежащего к этому углу.
Один из острых углов равен 30°. Найдите длину катета, прилежащего к этому углу.

18. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.

19. Какое из следующих утверждений верно?
1. Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2. Все углы ромба равны.
3. Если диагонали выпуклого четырехугольника равны и перпендикулярны, то этот четырехугольник является квадратом.
В ответ запишите номер выбранного утверждения.
20. Упростите выражение:
![]()
21. Имеются два сосуда, содержащие 24 кг и 26 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 39% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится в первом растворе?
22. Известно, что парабола проходит через точку ![]() и ее вершина находится в начале координат. Найдите уравнение этой параболы и вычислите, в каких точках она пересекает прямую
и ее вершина находится в начале координат. Найдите уравнение этой параболы и вычислите, в каких точках она пересекает прямую ![]()
23. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 16, DC = 24, AC = 25 .
24. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке E стороны BC. Докажите, что E — середина BC.
25. В треугольнике ABC известны длины сторон AB = 14, AC = 98, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 05, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 06, задачи 1-25
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырех цифр без пробелов, запятых и других дополнительных символов.
| Объекты | коридор | кладовая | кухня | гостиная |
| Цифры |
|
|
|
|
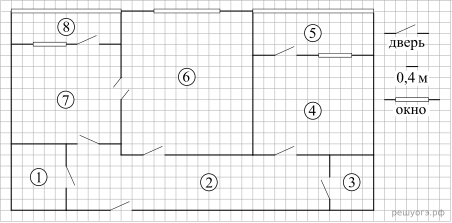
На рисунке изображен план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка.
Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора — дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пройти на одну из застекленных лоджий. Самое большое по площади помещение — гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застекленную лоджию.
2. Паркетная доска размером 20 см на 80 см продается в упаковках по 14 штук. Сколько упаковок паркетной доски понадобилось, чтобы выложить пол в гостиной?
3. Найдите площадь гостиной. Ответ дайте в квадратных метрах.
4. На сколько процентов площадь кухни больше площади лоджии, примыкающей к кухне?
5. В квартире планируется подключить интернет. Предполагается, что трафик составит 650 Мб в месяц, и исходя из этого выбирается наиболее дешевый вариант. Интернет–провайдер предлагает три тарифных плана.
| Тарифный план | Абонентская плата | Плата за трафик |
| План «500» | 600 руб. за 500 Мб трафика в месяц | 2 руб. за 1 Мб сверх 500 Мб |
| План «1000» | 820 руб. за 1000 Мб трафика в месяц | 1,5 руб. за 1 Мб сверх 1000 Мб |
| «Безлимитный» | 900 руб. за неограниченное количество Мб трафика | — |
Сколько рублей нужно будет заплатить за интернет за месяц, если трафик действительно будет равен 650 Мб?
6. Вычислите: ![]()
7. Одна из точек, отмеченных на координатной прямой, соответствует числу ![]() Какая это точка?
Какая это точка?
![]()
1) M 2) N 3) P 4) Q
8. Найдите значение выражения
![]() при
при ![]()
9. Решите уравнение:
![]()
10. Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.
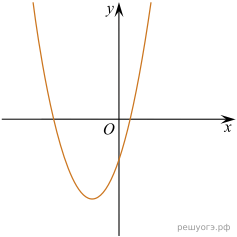
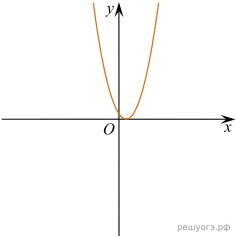
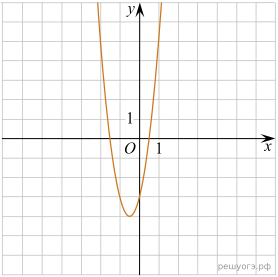
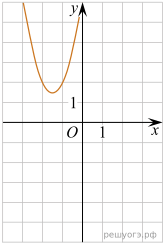
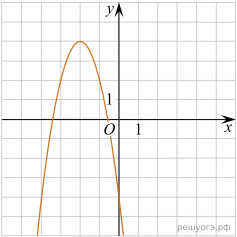
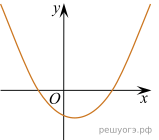
11. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
| А)
| В)
| ||||||
| Б)
| 1) 2) 3)
|
12. Зная длину своего шага, человек может приближенно подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошел человек, если l = 70 см, n =1400 ? Ответ выразите в километрах.
13. Укажите решение неравенства ![]()
1)![]() ; 2)
; 2)![]()
3)![]() 4)
4)![]() .
.
14. Компания «Альфа» начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 3500 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла прибыль 100% от капитала предыдущего года. А компания «Бета» начала инвестировать средства в другую отрасль в 2004 году, имея капитал в размере 4500 долларов, и, начиная с 2005 года, ежегодно получала прибыль, составляющую 300% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2008 года, если прибыль из оборота не изымалась?
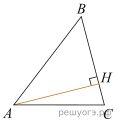
15. В остроугольном треугольнике ABC высота AH равна ![]() а сторона AB равна 8.
а сторона AB равна 8.
Найдите cosB.
16. Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC = 47° и ∠OAB = 38°. Найдите угол BCO. Ответ дайте в градусах.
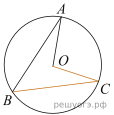
17. В трапеции ABCD известно, что AD=8, BC=6, а ее площадь равна 49. Найдите площадь треугольника ABC.
18. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.

19. Какие из следующих утверждений верны?
1) Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету.
2) Диагонали ромба перпендикулярны.
3) Существуют три прямые, которые проходят через одну точку.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
20. Решите уравнение ![]()
21. Расстояние между городами А и В равно 120 км. Из города А в город В выехал автомобиль, а через 90 минут следом за ним со скоростью 100 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.
22. Постройте график функции ![]() и определите, при каких значениях c прямая
и определите, при каких значениях c прямая ![]() имеет с графиком ровно три общие точки.
имеет с графиком ровно три общие точки.
23. Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD = 25.
24. В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CMD.
25. Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 12 см, тангенс угла ABC равен 2,4 . Найдите радиус вписанной окружности треугольника ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 06, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 07, задачи 1-25
1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 65 см?
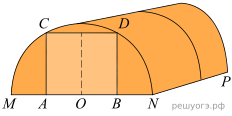
Алексей Юрьевич решил построить на дачном участке теплицу длиной NP=5,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Алексей Юрьевич заказывает металлические дуги в форме полуокружностей длиной 5,3 м каждая и пленку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B— середины отрезков MO и ON соответственно.
2. Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.
3. Найдите примерную площадь участка внутри теплицы в квадратных метрах. Ответ округлите до целых.
4. Сколько квадратных метров пленки нужно купить для теплицы с учетом передней и задней стенок, включая дверь? Для крепежа пленку нужно покупать с запасом 10 %. Число π возьмите равным 3,14. Ответ округлите до целых.
5. Найдите примерную высоту входа в теплицу в метрах. Число π возьмите равным 3,14. Ответ округлите до десятых.
6. Найдите значение выражения 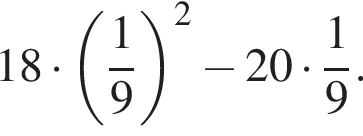
7. На координатной прямой отмечены числа x и y. Какое из следующих утверждений об этих числах верно?
![]()
В ответе укажите номер правильного варианта.
1) ![]() и
и ![]() ; 2)
; 2) ![]() и
и ![]()
3) ![]() и
и ![]() ; 4)
; 4) ![]() и
и ![]()
8. Найдите значение выражения
![]() при
при ![]()
9. Найдите корни уравнения ![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что стрелок первый раз попал в мишени, а последние два раза промахнулся.
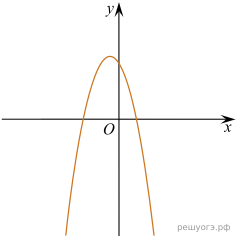
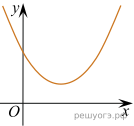
11. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам.
| А)
| Б)
| ||||||
| В)
| 1) 2) 3)
|
12. Площадь треугольника ![]() можно вычислить по формуле
можно вычислить по формуле ![]() где a — сторона треугольника, h — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону
где a — сторона треугольника, h — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону ![]() если площадь треугольника равна
если площадь треугольника равна ![]() а высота h равна 14 м.
а высота h равна 14 м.
13. Укажите решение неравенства ![]()
1)![]() 2)
2)![]()
3)![]() 4)
4)![]()
14. Бригада маляров красит забор длиной 270 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 90 метров забора. Определите, сколько дней бригада маляров красила весь забор.
15. Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.
16. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 62°. Найдите величину угла BOC. Ответ дайте в градусах.

17. Площадь параллелограмма ABCD равна 6. Точка E — середина стороны AB. Найдите площадь трапеции EBCD.

18. На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите длину его большей диагонали.

19. Какое из следующих утверждений верно?
1. Если диагонали параллелограмма равны, то этот параллелограмм является ромбом.
2. Тангенс любого острого угла меньше единицы.
3. Сумма углов равнобедренного треугольника равна 180 градусам.
В ответ запишите номер выбранного утверждения.
20. Решите уравнение
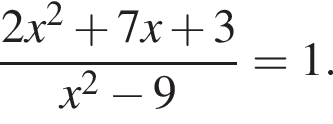
21. Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 час. За сколько часов наполняет бассейн одна вторая труба?
22. Постройте график функции
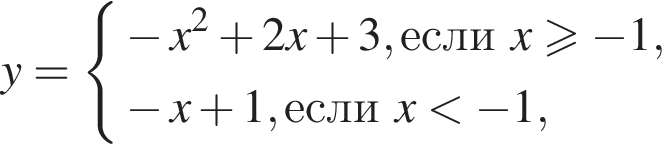
и определите, при каких значениях m прямая
y = m имеет с графиком ровно две общие точки.
23. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 13, DC = 65, AC = 42.
24. На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рис.). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
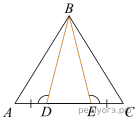
25. В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 136. Найдите стороны треугольника ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 07, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 08, задачи 1-25
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырех цифр.
| Объекты | Балкон | Детская комната | Гостиная | Кухня |
| Цифры |
|
|
|
|

На плане изображена схема квартиры (сторона каждой клетки на схеме равна 1 м). Вход и выход осуществляются через единственную дверь.
При входе в квартиру расположена прихожая, отмеченная цифрой 6. Из прихожей можно попасть в гостиную, расположенную справа от нее. В квартире есть балкон, занимающий наименьшую площадь. Перед входом в прихожую располагается спальня, а справа от нее — детская комната, в которую можно попасть только из спальни. Рядом со спальней расположен совмещенный санузел площадью 12 м2. Кроме того, в квартире есть кухня.
Пол в гостиной планируется покрыть паркетной доской длиной 1 м и шириной 0,25 м.
В квартире проведены газопровод и электричество.
2. Паркетная доска продается в упаковках по 16 шт. Сколько упаковок с паркетной доской требуется купить, чтобы покрыть пол в гостиной?
3. Найдите площадь, которую занимают спальная комната и детская. Ответ дайте в квадратных метрах.
4. Найдите расстояние d между противоположными углами кухни в метрах.
В ответ запишите ![]()
5. Хозяин квартиры планирует установить в квартире плиту для готовки. Он рассматривает два варианта: газовая плита или электроплитка. Цены на плиты, данные о потреблении и тарифах оплаты даны в таблице.
|
| Цена | Расход газа/Потребл. мощность | Стоимость газа /электро-энергии |
| Газовая плита | 43 730 руб. | 1,2 куб. м/ч | 5,3 руб./куб. м |
| Электро- плитка | 17 000 руб. | 6,2 кВт | 3,9 руб./(кВт · ч ) |
Обдумав оба варианта, хозяин решил установить газовую плиту. Через сколько часов непрерывного использования экономия от использования газовой плиты вместо электрической компенсирует разность в стоимости установки газовой плиты и электроплитки?
6. Найдите значение выражения 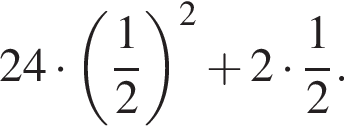
7. Одна из точек, отмеченных на координатной прямой, соответствует числу ![]() . Какая это точка?
. Какая это точка?
![]()
1) точка M 2) точка N 3) точка P 4) точка Q
8. Найдите значение выражения
![]() при
при ![]()
9. Решите уравнение ![]()
10. Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5.
11. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам
| А)
| Б)
| ||||||
| В)
| 1) 2) 3)
|
12. Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объем (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T = 700 К, P = 20 941,2 Па, V = 9,5 м3.
13. На каком рисунке изображено множество решений неравенства ![]() ?
?
| 1)
| 2)
|
| 3)
| 4)
|
14. В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах — одно штрафное очко, за каждый последующий — на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков?
15. В трапеции ABCD известно, что ![]()
![]() и
и ![]() Найдите угол CAD. Ответ дайте в градусах.
Найдите угол CAD. Ответ дайте в градусах.
16. В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 136°. Найдите вписанный угол ACB. Ответ дайте в градусах.
17. В трапеции ABCD известно, что AD=6, BC=5, а ее площадь равна 22. Найдите площадь треугольника ABC.

18. Найдите тангенс угла AOB, изображенного на рисунке.

19. Какие из следующих утверждений верны?
1. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2. В тупоугольном треугольнике все углы тупые.
3. Любой квадрат является прямоугольником.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
20. Решите неравенство
![]()
21. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 50 км/ч и 40 км/ч. Длина товарного поезда равна 1350 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 9 минутам. Ответ дайте в метрах.
22. Постройте график функции
![]()
и определите, при каких значениях параметра c прямая ![]() имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
23. Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
24. В остроугольном треугольнике ABC, точки A, C, центр описанной окружности O и точка пересечения высот H лежат на одной окружности. Докажите, что угол ABC равен 60°.
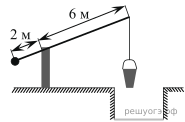
25. На рисунке изображен колодец с «журавлем». Короткое плечо имеет длину 2 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 08, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 09, задачи 1-25
1. Установите соответствие между массами и номерами печей.
Заполните таблицу, в бланк ответов перенесите последовательность трех цифр без пробелов, запятых и других дополнительных символов.
| Масса (кг) | 15 | 40 | 48 |
| Номер печи |
|
|
|
Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проема 1,8 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трех печей.
| Номер печи | Тип | Объем помещения | Масса | Стоимость |
| 1 | Дровяная | 8-12 | 40 | 18 000 |
| 2 | Дровяная | 10-16 | 48 | 19 500 |
| 3 | Электрическая | 9-15,5 | 15 | 15 000 |
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдется в 6500 руб.
2. Найдите объем парного отделения строящейся бани. Ответ дайте в кубических метрах.
3. Во сколько рублей обойдется покупка электрической печи с установкой и доставкой, если доставка печи до дачного участка будет стоить 800 рублей?
4. На дровяную печь, масса которой 48 кг, сделали скидку 10%. Сколько рублей стала стоить печь?
5. Хозяин выбрал дровяную печь (рис. 1). Чертеж передней панели печи показан на рисунке 2.
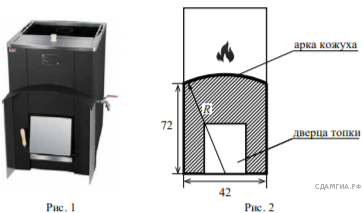
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (см. рис. 2). Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
6. Найдите значение выражения: ![]()
7. Между какими числами заключено число ![]()
1) 55 и 57; 2) 3 и 4; 3) 19 и 21; 4) 7 и 8
8. Упростите выражение ![]() и найдите его значение при
и найдите его значение при ![]() и
и ![]()
В ответе запишите найденное значение.
9. Найдите корни уравнения ![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. На экзамене 60 билетов, Олег не выучил 12 из них. Найдите вероятность того, что ему попадется выученный билет.
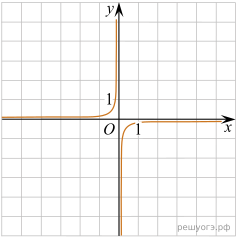
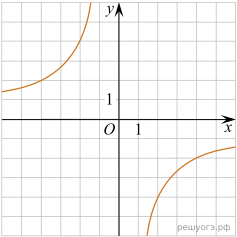
11. На одном из рисунков изображен график функции ![]() Укажите номер этого рисунка.
Укажите номер этого рисунка.
| 1) | 2) |
| 3) | 4) |
12. В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле C = 150+11 ⋅ (t − 5) , где t — длительность поездки, выраженная в минутах (t 5). Пользуясь этой формулой, рассчитайте стоимость 13-минутной поездки.
13. Найдите наибольшее значение x, удовлетворяющее системе неравенств
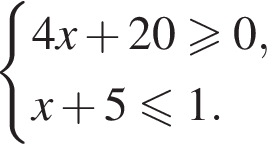
14. В амфитеатре 13 рядов. В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
15. В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.

16. На отрезке AB выбрана точка C так, что ![]() и
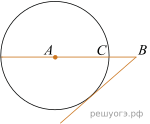
и ![]() Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведенной из точки B к этой окружности.
Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведенной из точки B к этой окружности.
17. Площадь прямоугольного треугольника равна ![]() Один из острых углов равен 60°. Найдите длину катета, прилежащего к этому углу.
Один из острых углов равен 60°. Найдите длину катета, прилежащего к этому углу.

18. На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите его площадь.
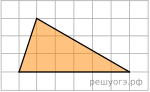
19. Какие из следующих утверждений верны?
1) Каждая сторона треугольника меньше разности двух других сторон.
2) В равнобедренном треугольнике имеется не более двух равных углов.
3) Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны.
4) В треугольнике ABC, для которого AB = 3, BC = 4, AC = 5, угол C наименьший.
20. Один из корней уравнения ![]() равен −1. Найдите второй корень.
равен −1. Найдите второй корень.
21. Из пунктов А и В, расстояние между которыми 19 км, вышли одновременно навстречу друг другу два пешехода и встретились в 9 км от А. Найдите скорость пешехода, шедшего из А, если известно, что он шел со скоростью, на 1 км/ч большей, чем пешеход, шедший из В, и сделал в пути получасовую остановку.
22. Постройте график функции
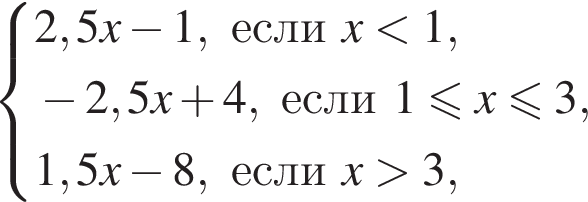
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
23. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключенная внутри этого угла, равна 110°.

24. Внутри параллелограмма ABCD выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади параллелограмма.
25. Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 09, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 10, задачи 1-25
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырех цифр без пробелов и других дополнительных символов.
| Объекты | Хутор Камышино | Село Большое | Озеро Круглое | Деревня Дубки |
| Цифры |
|
|
|
|
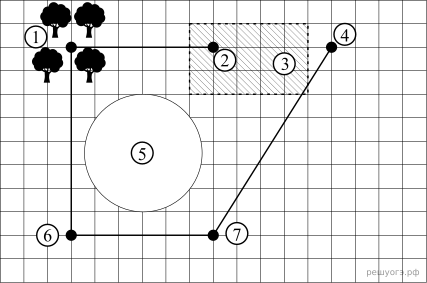
На плане (см. рис.) изображена местность, прилегающая к озеру Круглому. Для удобства план нанесен на квадратную сетку, сторона каждого квадрата которой равна 500 м. Населенные пункты обозначены на плане жирными точками.
Рядом с озером Круглое находится болото, обозначенное на плане штриховкой. На болоте расположен хутор Камышино. От хутора Камышино проложена дорога к деревне Дубки, вокруг которой имеются дубовые рощи. Далее дорога идет к селу Большое, расположенному по другую сторону озера от хутора Камышино. Село Большое соединено также дорогой с деревней Малая, обозначенной на плане цифрой 7. Деревня Малая, в свою очередь, соединена дорогой с деревней Дальней (отмечена цифрой 4). Преобладающая часть изображенной на плане местности — это поля, используемые для выращивания злаков.
2. Автомобиль расходует в среднем 9 л топлива на 100 км пути. Сколько литров топлива израсходует автомобиль при поездке из хутора Камышино в деревню Малая по имеющимся дорогам?
3. Найдите площадь (в км2) болота, отмеченного на плане.
4. Найдите расстояние (в метрах) по прямой от хутора Камышино до села Большое.
5. Для улучшения сообщения между населенными пунктами планируется построить еще одну дорогу: из хутора Камышино в деревню Малая либо из хутора Камышино в деревню Дальняя. Дорога должна соединить населенные пункты по прямой. Цена прокладки дороги по полю равна 10 млн рублей за 1 км, по болоту – 20 млн рублей за 1 км. Из указанных двух вариантов дороги выберите тот, стоимость которого будет ниже. В ответе укажите стоимость (в млн рублей) выбранного варианта дороги.
6. Найдите значение выражения ![]()
7. На координатной прямой отмечены числа
x, y и z.
![]()
Какая из разностей z − x, z − y, y − x отрицательна?
В ответе укажите номер правильного варианта.
1) z − x; 2) z − y; 3) y − x; 4) ни одна из них
8. Найдите значение выражения 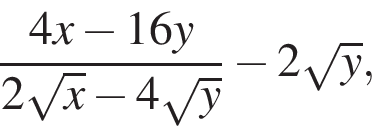 если
если ![]()
9. Найдите корни уравнения ![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. Определите вероятность того, что при бросании кубика выпало число очков,
не большее 3.
11. Установите соответствие между функциями и их графиками. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам
| 1)
| 2)
| ||||||
| 3)
| А) Б) B)
|
12. В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле ![]() где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 8 колец. Ответ дайте в рублях.
где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 8 колец. Ответ дайте в рублях.
13. Укажите решение системы неравенств:
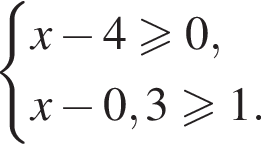
| 1)
| 2)
|
| 3)
| 4)
|
14. Часть программы тренировок Арсения заключается в беге на беговой дорожке. На первой тренировке необходимо бежать 15 минут, на каждой следующей время пробежки увеличивается на 7 минут. За сколько тренировок Арсений проведет на беговой дорожке в общей сложности 2 часа 25 минут, если будет следовать программе? (В ответе укажите только число.)
15. В треугольнике ABC известно, что ![]()
![]() угол C равен 90°. Найдите радиус описанной окружности этого треугольника.
угол C равен 90°. Найдите радиус описанной окружности этого треугольника.

16. На отрезке AB выбрана точка C так, что ![]() и
и ![]() Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведенной из точки B к этой окружности.
Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведенной из точки B к этой окружности.

17. В треугольнике ABC DE — средняя линия. Площадь треугольника CDE равна 9. Найдите площадь треугольника ABC.
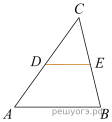
18. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.

19. Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.
2) Любые две прямые имеют не менее одной общей точки.
3) Через любую точку проходит более одной прямой.
4) Любые три прямые имеют не менее одной общей точки.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Решите неравенство ![]()
21. Первые 500 км автомобиль ехал со скоростью 100 км/ч, следующие 100 км — со скоростью 50 км/ч, а последние 165 км — со скоростью 55 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
22. Постройте график функции ![]()
Определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.
23. На сторонах угла BAC, равного 20°, и на его биссектрисе отложены равные отрезки AB, AC и AD. Определите величину угла BDC.
24. Основания BC и AD трапеции ABCD равны соответственно 2 и 32, BD = 8. Докажите, что треугольники CBD и BDA подобны.
25. В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 104. Найдите стороны треугольника ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 10, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 11, задачи 1-25
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населенные пункты. В ответ запишите полученную последовательность пяти цифр.
| Насел. пункты | д. Мальцево | с. Игнатьево | д. Сосновка | п. Дачный | д. Анино |
| Цифры |
|
|
|
|
|
Миша летом отдыхает у дедушки и бабушки в деревне Анино. Миша с дедушкой собираются съездить на велосипедах в село Игнатьево на железнодорожную станцию. Из Анино в Игнатьево можно проехать по шоссе до деревни Сосновка, где нужно свернуть под прямым углом направо на другое шоссе, ведущее в Игнатьево через поселок Дачный. Из Анино в Игнатьево можно проехать через поселок Дачный и не заезжая в Сосновку, но тогда первую часть пути надо будет ехать по прямой лесной дорожке. Есть и третий маршрут: доехать по прямой тропинке мимо птицефабрики до деревни Мальцево и там, повернув налево, по шоссе добраться до Игнатьево. По шоссе Миша с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке — 15 км/ч. Расстояние по шоссе от Анино до Сосновки равно 15 км, от Игнатьево до Сосновки — 24 км, от Игнатьево до Дачного — 16 км, а от Игнатьево до Мальцево — 8 км.
2. Нас сколько процентов скорость, с которой едут Миша с дедушкой по тропинке, меньше их скорости по шоссе?
3. Найдите расстояние от деревни Анино до поселка Дачного по лесной дорожке. Ответ дайте в километрах.
4. Сколько минут затратят на дорогу Миша с дедушкой, если поедут на станцию через Сосновку?
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Миша с дедушкой, если поедут этим маршрутом.
6. Найдите значение выражения (4,9 · 10− 3)(4 · 10− 2).
7. Известно, что число m отрицательное. На каком из рисунков точки с координатами ![]() расположены на координатной прямой в правильном порядке?
расположены на координатной прямой в правильном порядке?
| 1)
| 2)
|
| 3)
| 4)
|
В ответе укажите номер правильного варианта.
8. Сократите дробь ![]()
9. Решите уравнение ![]()
10. Игральный кубик бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел четна.
11. Установите соответствие между графиками функций и формулами, которые их задают. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам.
| А)
| Б)
| ||||||
| В)
| 1) 2) 3)
|
12. Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 588 ватт, а сила тока равна 7 амперам.
13. На каком рисунке изображено множество решений системы неравенств 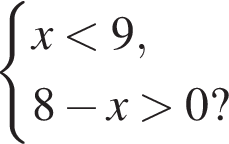
| 1)
| 2)
| ||
| 3)
| 4)
|
| |
14. Мать дарит каждой из пяти своих дочерей в день рождения, начиная с пяти лет, столько книг, сколько дочери лет. Возрасты пяти дочерей составляют арифметическую прогрессию, разность которой равна 2. Сколько лет было старшей дочери, когда у них составилась библиотека общей численностью в 495 книг?
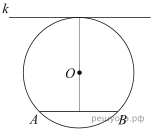
15. Радиус окружности с центром в точке O равен 97, длина хорды AB равна 130 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.
16. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором ![]() и
и ![]() Найдите угол BOC. Ответ дайте в градусах.
Найдите угол BOC. Ответ дайте в градусах.

17. В трапеции ABCD известно, что AD=5, BC=4, а ее площадь равна 81. Найдите площадь треугольника ABC.

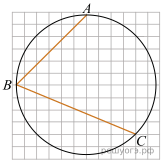
18. Найдите угол ABC. Ответ дайте в градусах.
19. Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит ее на два равных треугольника.
3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Решите систему уравнений 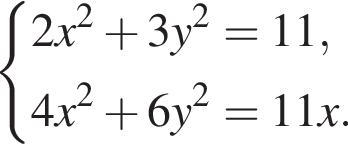
21. Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошел первый круг 20 минут назад. Найдите скорость первого бегуна, если известно, что она на 8 км/ч меньше скорости второго.
22. Постройте график функции ![]()
Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
23. Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно
45° и 150°, а CD = 26.
24. На стороне AC треугольника ABC отмечены точки D и E так, что ![]() Докажите, что если
Докажите, что если ![]() то
то ![]() .
.
25. Стороны AC, AB, BC треугольника ABC равны 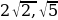 и 1 соответственно. Точка K расположена вне треугольника ABC, причем отрезок KC пересекает отрезок AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если
и 1 соответственно. Точка K расположена вне треугольника ABC, причем отрезок KC пересекает отрезок AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ![]() 90°.
90°.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 11, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 12, задачи 1-25
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | жилой дом | баня | гараж | теплица |
| Цифры |
|
|
|
|
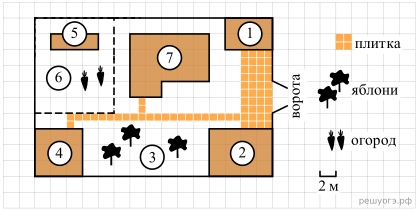
На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв. м, а чуть подальше — жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6).
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером ![]() Между гаражом и сараем находится площадка, вымощенная такой же плиткой.
Между гаражом и сараем находится площадка, вымощенная такой же плиткой.
К участку подведено электричество. Имеется магистральное газоснабжение.
2. Плитки для садовых дорожек продаются в упаковках по 10 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
3. Найдите периметр фундамента жилого дома. Ответ дайте в метрах.
4. На сколько процентов площадь, которую занимает баня, меньше площади, которую занимает гараж?
5. Хозяин участка планирует установить в жилом доме систему отопления. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
|
| Нагреватель (котел) | Прочее оборудование и монтаж | Средн. расход газа/ средн. потребл. мощность | Стоимость газа/ электроэнергии |
| Газовое отопление | 20 000 руб. | 15 370 руб. | 1,6 куб. м/ч | 4,9 руб./куб. м |
| Электр. отопление | 15 000 руб. | 14 000 руб. | 4,9 кВт | 4,2 руб./( кВт |
Обдумав оба варианта, хозяин решил установить газовое отопление. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разницу в стоимости покупки и установки газового и электрического оборудования?
6. Найдите значение выражения 45+0,6 · (−10)2.
7. Одна из точек, отмеченных на координатной прямой, соответствует числу ![]()
Какая это точка?

1) точка А; 2) точка В; 3) точка С; 4) точка D
8. Найдите значение выражения
![]()
при ![]()
9. Решите уравнение
![]()
10. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.
11. Установите соответствие между функциями и их графиками. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам.
| 1)
| 2)
| А) Б) В) | ||||||
| 3)
| 4)
|
|
12. Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле a = ω2R, где ω — угловая скорость (в с −1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 9 с−1, а центростремительное ускорение равно 648 м/с2.
13. На каком рисунке изображено множество решений неравенства ![]() ?
?
| 1)
| 2)
| ||
| 3)
| 4)
|
| |
14. Бизнесмен Коржов получил в 2000 году прибыль в размере 1 400 000 рублей. Каждый следующий год его прибыль увеличивалась на 20% по сравнению с предыдущим годом. Сколько рублей составила прибыль Коржова за 2004 год?
15. Четырехугольник ABCD вписан в окружность. Угол ABD равен 25°, угол CAD равен 41°. Найдите угол ABC. Ответ дайте в градусах.

16. Касательные в точках A и B к окружности с центром O пересекаются под углом 14°. Найдите угол ABO. Ответ дайте в градусах.

17. В трапеции ABCD известно, что AD = 2, BC = 1, а ее площадь равна 60. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
18. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите ее площадь.
19. Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
20. Решите неравенство ![]()
21. Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ, состоящий из 112 деталей, на 4 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
22. При каком значении р прямая ![]() имеет с параболой
имеет с параболой ![]() ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении
ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении ![]()
23. В треугольнике ABC угол С равен 90°, радиус вписанной окружности равен 2. Найдите площадь треугольника ABC, если AB = 12.
24. В параллелограмме ABCD проведены высоты BH и BE к сторонам AD и CD соответственно, при этом BH = BE. Докажите, что ABCD — ромб.
25. Основание AC равнобедренного треугольника ABC равно 18. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 12, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 13, задачи 1-25
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырех цифр.
| Объекты | Книжный шкаф | Диван | Торшер | Стул |
| Цифры |
|
|
|
|

Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели в гостиной после ремонта. Сторона каждой клетки равна 0,4 м. Гостиная имеет прямоугольную форму. Единственная дверь гостиной деревянная, в стене напротив двери расположено окно. Справа от двери будет поставлен комод, слева от двери у стены будет собран книжный шкаф. В глубине комнаты у стены планируется поставить диван. Перед книжным шкафом будет поставлено кресло. Справа от дивана будет стоять торшер. Площадь, занятая диваном, по плану будет равна 1,28 м2. У стены справа от двери планируется поставить письменный стол, а перед ним поставить стул. Пол гостиной (в том числе там, где будет стоять мебель) планируется покрыть паркетной доской размером 40 см × 20 см. Кроме того, владелец квартиры планирует смонтировать в гостиной электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под книжный шкаф, кресло, диван и комод, а также на участок площадью 0,16 м2 между диваном и торшером.
2. Паркетная доска продается в упаковках по 15 штук. Сколько упаковок с паркетной доской нужно купить, чтобы покрыть пол гостиной?
3. Найдите площадь той части гостиной, на которой будет смонтирован электрический подогрев пола. Ответ дайте в м2.
4. Найдите расстояние d между противоположными углами кресла (диагональ). Ответ дайте в метрах в формате ![]()
5. Владелец квартиры выбирает торшер из двух моделей А и Б. Цена торшеров и их среднее суточное потребление электроэнергии указаны в таблице. Цена электроэнергии составляет 4 рубля за кВт · ч.
| Модель | Цена торшера (руб.) | Среднее потребление электроэнергии в сутки, кВт · ч |
| А | 2 000 | 0,2 |
| Б | 1 200 | 0,3 |
Обдумав оба варианта, владелец квартиры выбрал модель А. Через сколько лет непрерывной работы экономия от меньшего расхода электроэнергии окупит разницу в цене этих торшеров? Ответ округлите до целого числа в большую сторону.
6. Найдите значение выражения ![]()
7. Какому из данных промежутков принадлежит число ![]() ?
?
| 1) [0,4; 0,5] | 2) [0,5; 0,6] | 3) [0,6; 0,7] | 4) [0,7; 0,8] |
8. Найдите значение выражения
![]() при
при ![]()
9. Решите систему уравнений
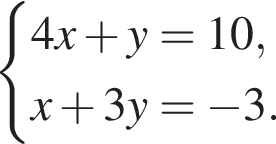 В ответ запишите х + у.
В ответ запишите х + у.
10. Для экзамена подготовили билеты с номерами от 1 до 25. Какова вероятность того, что наугад взятый учеником билет имеет номер, являющийся двузначным числом?
11. Установите соответствие между графиками функций и формулами, которые их задают. Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
| А) | Б) | ||||||
| В) | 1) 2) 3) 4)
|
12. Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 63° по шкале Фаренгейта? Ответ округлите до десятых.
13. Решите неравенство ![]()
В ответе укажите номер правильного варианта.
1) (− ∞; 8); 2) (− ∞; 1); 3) (8; +∞); 4) (1; +∞)
14. Рабочие прокладывают тоннель длиной 500 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 3 метра тоннеля. Определите, сколько метров тоннеля проложили рабочие в последний день, если вся работа была выполнена за 10 дней.
15. Тангенс острого угла прямоугольной трапеции равен ![]() Найдите ее большее основание, если меньшее основание равно высоте и равно 58.
Найдите ее большее основание, если меньшее основание равно высоте и равно 58.

16. На отрезке AB выбрана точка C так, что ![]() и
и ![]() Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведенной из точки B к этой окружности.
Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведенной из точки B к этой окружности.

17. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
18. Найдите угол ABC. Ответ дайте в градусах.
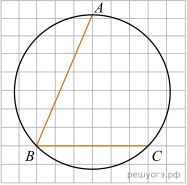
19. Какое из следующих утверждений верно?
1. Площадь квадрата равна произведению двух его смежных сторон.
2. Диагональ трапеции делит ее на два равных треугольника.
3. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
В ответ запишите номер выбранного утверждения.
20. Решите систему уравнений 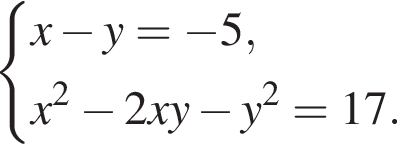
21. Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится во втором растворе?
22. Постройте график функции ![]() и определите, при каких значениях c прямая
и определите, при каких значениях c прямая ![]() имеет с графиком ровно три общие точки.
имеет с графиком ровно три общие точки.
23. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 18, AC = 42, NC = 40.
24. Основания BC и AD трапеции ABCD равны соответственно 5 и 45, BD = 15. Докажите, что треугольники CBD и BDA подобны.
25. В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 14, BC = 7.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 13, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 14, задачи 1-25
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырех цифр без пробелов и других дополнительных символов.
| Объекты | Стул | Диван | Журнальный столик | Кресло |
| Цифры |
|
|
|
|

Владелец собирается провести ремонт своей квартиры. На плане изображена предполагаемая расстановка мебели в гостиной после ремонта. Сторона каждой клетки равна 0,4 м. Гостиная имеет прямоугольную форму. Единственная дверь гостиной деревянная, в стене напротив двери расположено окно. Справа от двери будет поставлен письменный стол, а к нему приставлен стул, слева от двери у стены будет собран книжный шкаф. В глубине комнаты у стены планируется поставить диван, а перед ним — журнальный столик. Слева от дивана будет стоять торшер. Площадь, занятая диваном, по плану будет равна 1,6 м2. В оставшемся свободным углу планируется поставить кресло. Пол гостиной (в том числе там, где будет стоять мебель) планируется покрыть паркетной доской размером 40 см × 10 см. Кроме того, владелец квартиры планирует смонтировать в гостиной электрический подогрев пола. Чтобы сэкономить, владелец не станет подводить обогрев под книжный шкаф, кресло и диван.
2. Паркетная доска продается в упаковках по 25 штук. Сколько упаковок с паркетной доской нужно купить, чтобы покрыть пол гостиной?
3. Найдите площадь той части гостиной, на которой будет смонтирован электрический подогрев пола. Ответ дайте в м2.
4. Найдите расстояние от дивана до письменного стола (расстояние между двумя ближайшими точками по прямой) в метрах.
5. Владелец квартиры выбирает торшер из двух моделей А и Б. Цена торшеров и их среднее суточное потребление электроэнергии указаны в таблице. Цена электроэнергии составляет 5 рублей за кВт · ч.
| Модель | Цена торшера (руб) | Среднее потребление электроэнергии в сутки, кВт · ч |
| А | 2 100 | 0,3 |
| Б | 1 370 | 0,4 |
Обдумав оба варианта, владелец квартиры выбрал модель А. Через сколько лет непрерывной работы экономия от меньшего расхода электроэнергии окупит разницу в цене этих торшеров? Ответ округлите до целого числа.
6. Найдите значение выражения 9,3 + 7,8.
7. О числах a и c известно, что ![]() Какое из следующих неравенств неверно?
Какое из следующих неравенств неверно?
1) ![]() ; 2)
; 2) ![]()
3) ![]() ; 4)
; 4) ![]()
8. Упростите выражение
![]() и найдите его значение при
и найдите его значение при ![]() и
и ![]() В ответе запишите найденное значение.
В ответе запишите найденное значение.
9. Найдите корни уравнения ![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. В магазине канцтоваров продается 264 ручки: 38 красных, 30 зеленых, 8 фиолетовых, остальные синие и черные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или черной.
11. Найдите значение a по графику функции ![]() изображенному на рисунке.
изображенному на рисунке.
|
|
|
12. В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле C = 150+11 ⋅ (t − 5) , где t — длительность поездки, выраженная в минутах (t 5). Пользуясь этой формулой, рассчитайте стоимость 13-минутной поездки.
13. Решите неравенство ![]()
В ответе укажите номер правильного варианта.
1) ![]() ; 2)
; 2) ![]()
3) ![]() ; 4)
; 4) ![]()
14. Рабочие прокладывают тоннель длиной 99 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 7 метров туннеля. Определите, сколько метров туннеля проложили рабочие в последний день, если вся работа была выполнена за 9 дней.
15. В прямоугольном треугольнике катет и гипотенуза равны 40 и 41 соответственно. Найдите другой катет этого треугольника.

16. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 124°. Найдите величину угла BOC. Ответ дайте в градусах.

17. Площадь параллелограмма ABCD равна 184. Точка E — середина стороны AB. Найдите площадь трапеции EBCD.

18. Найдите тангенс угла AOB.

19. Укажите номера верных утверждений.
1) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
2) Смежные углы равны.
3) Медиана равнобедренного треугольника, проведенная к его основанию, является его высотой.
20. Сократите дробь
![]()
21. Пристани ![]() и
и ![]() расположены на реке, скорость течения которой на этом участке равна 3 км/ч. Лодка проходит туда и обратно без остановок со средней скоростью 8 км/ч. Найдите собственную скорость лодки.
расположены на реке, скорость течения которой на этом участке равна 3 км/ч. Лодка проходит туда и обратно без остановок со средней скоростью 8 км/ч. Найдите собственную скорость лодки.
22. Постройте график функции
![]() Определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.
Определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.
23. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключенная внутри этого угла, равна 130°.
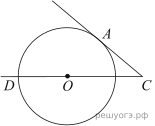
24. В окружности через середину O хорды AC проведена хорда BD так, что дуги AB и CD равны. Докажите, что O — середина хорды BD.
25. На стороне BC остроугольного треугольника ABC (AB ≠ AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD = 81, MD = 9, H — точка пересечения высот треугольника ABC. Найдите AH.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 14, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 15, задачи 1-25
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырех цифр.
| Объекты | Магазин | Фитнес‐центр | Мастерская | Дом, где живет Олег |
| Цифры |
|
|
|
|
На плане (см. рис.) изображен район города, в котором проживает Вика. Сторона каждой клетки на плане равна 15 м. Рядом с домом Вики, обозначенным на плане цифрой 4, находится одноэтажный магазин площадью 900 м2 и фитнес‐центр. В 15 м от магазина расположен дом, где живет одноклассник Вики Артем. В 30 м от детской площадки находится дом, где живет Олег. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к угловому дому, где живет дедушка Вики. Рядом с ним находится мастерская по ремонту бытовой техники. Через дорогу от дома дедушки расположен рынок, а недалеко от него – мебельный центр площадью 2025 м2.
2. Детскую площадку решили покрыть резиновой плиткой размером 1 м × 1 м каждая. Плитка продается упаковками по 16 штук. Какое минимальное количество упаковок плитки необходимо приобрести?
3. Найдите суммарную площадь, которую занимают магазин и фитнес-центр. Ответ дайте в м2.
4. По периметру детской площадки планируется поставить забор. Найдите его длину (в метрах).
5. Фирма выбирает место для строительства гостиницы: в центре города или на его окраине. Стоимость прокладки 1 метра коммуникаций равна 5500 рублей. В гостинице планируется сдавать 500 номеров. Стоимость земли, цена строительства гостиницы и средняя стоимость номера даны в таблице.
| Место | Цена земли (млн руб.) | Цена строительства (млн руб.) | Длина коммуникаций (м) | Стоимость номера (руб./сутки) |
| Центр | 58,2 | 136 | 200 | 3200 |
| Окраина | 11,3 | 128 | 2800 | 2800 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько суток после начала сдачи номеров (при условии полной загрузки гостиницы) более высокая стоимость номеров компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций?
6. Найдите значение выражения
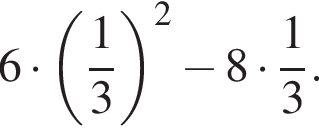
7. На координатной прямой отмечены числа a и b. Укажите номера неверных утверждений.
![]()
| 1) ab2 | 2) a − b 0 | 3) a + b | 4) ab |
8. Найдите значение выражения:
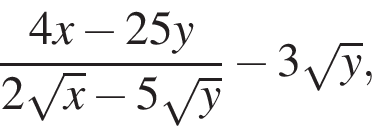 если
если ![]()
9. Решите уравнение
![]()
10. Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что стрелок первый раз попал в мишени, а последние два раза промахнулся.
11. На одном из рисунков изображена гипербола. Укажите номер этого рисунка.
| 1) | 2) |
| 3) | 4) |
12. В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле ![]() где t — длительность поездки, выраженная в минутах
где t — длительность поездки, выраженная в минутах ![]() Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.
Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.
13. Найдите наибольшее значение x, удовлетворяющее системе неравенств
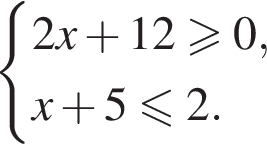
14. Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 11 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 81 километр.
15. Площадь прямоугольного треугольника равна ![]() Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.
Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.

16. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 63 , AO = 65 .
17. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 2 и HD = 64. Диагональ параллелограмма BD равна 80. Найдите площадь параллелограмма.
18. Найдите тангенс угла В треугольника ABC, изображенного на рисунке.

19. Какое из следующих утверждений верно?
1. Вписанный угол, опирающийся на диаметр окружности, прямой.
2. Если три угла одного треугольника равны соответственно трем углам другого треугольника, то такие треугольники равны.
3. Отношение площадей подобных треугольников равно коэффициенту подобия.
В ответ запишите номер выбранного утверждения.
20. Сократите дробь: ![]()
21. На пост главы администрации города претендовало три кандидата: Андреев, Борисов, Васильев. Во время выборов за Васильева было отдано в 1,5 раза больше голосов, чем за Андреева, а за Борисова — в 4 раза больше, чем за Андреева и Васильева вместе. Сколько процентов голосов было отдано за победителя?
22. При каких положительных значениях k прямая ![]() имеет с параболой
имеет с параболой ![]() ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
23. В прямоугольном треугольнике ABC с прямым углом C известны катеты:
![]()
![]() Найдите медиану CK этого треугольника.
Найдите медиану CK этого треугольника.
24. Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
25. Две касающиеся внешним образом в точке K окружности, радиусы которых равны 16 и 48, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 15, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 16, задачи 1-25
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырех цифр.
| Объекты | Город Гранюк | Деревня Астрелка | Хутор Южный | Город Гусевск |
| Цифры |
|
|
|
|
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живет бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до поселка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в поселок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идет ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.
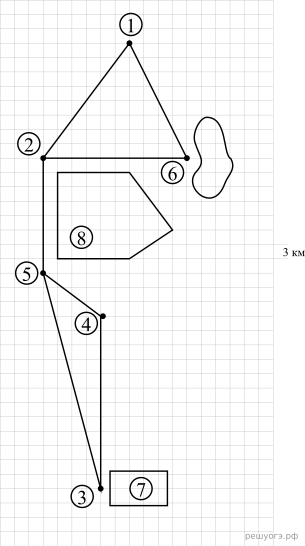
2. Ребята решили, что нужно взять в поездку чай в пакетиках определенного сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
3. Найдите площадь (в км2), которую занимает заказник.
4. Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в поселке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
5. Андрей выяснил, что его велосипед пришел в нерабочее состояние. Андрей посетил сайты интернет‐магазина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.
| Продукция | Цена в магазине «Вело» (руб.) | Цена в магазине «ОК» (руб.) | Срок доставки из магазина «ОК» (дни) |
| Подсветка для спиц | 190 | 180 | 3 |
| Шина вида «А» | 680 | 650 | 12 |
| Шина вида «Б» | 1680 | 1450 | 12 |
| Спица | 70 | 80 | 3 |
| Педаль вида «А» | 437 | 405 | 10 |
| Педаль вида «Б» | 860 | 750 | 10 |
| Тормоз вида «А» | 1130 | нет | 10 |
| Тормоз вида «Б» | нет | 2180 | 10 |
| Набор крепежных изделий | 740 | 765 | 14 |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепежных изделий. Сколько рублей Андрей потратит на набор запасных частей?
6. Найдите значение выражения 9,3 + 7,8.
7. На координатной прямой точки A, B, C и D соответствуют числам −0,39; −0,09; −0,93; 0,03.
![]()
Какой точке соответствует число −0,09?
1) A 2) B 3) C 4) D
8. Упростите выражение
![]() найдите его значение при
найдите его значение при ![]()
![]() В ответ запишите полученное число.
В ответ запишите полученное число.
9. Решите уравнение ![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 4 или 7.
11. На рисунке изображены графики функций вида ![]() Установите соответствие между знаками коэффициентов k и b и графиками функций. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам.
Установите соответствие между знаками коэффициентов k и b и графиками функций. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам.
| 1) | 3) | ||||||
| 2) | А) Б) В)
|
12. Закон Кулона можно записать в виде ![]() где F — сила взаимодействия зарядов (в ньютонах),
где F — сила взаимодействия зарядов (в ньютонах), ![]() и
и ![]() — величины зарядов (в кулонах), k — коэффициент пропорциональности (в Н·м2/Кл2 ), а r — расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда
— величины зарядов (в кулонах), k — коэффициент пропорциональности (в Н·м2/Кл2 ), а r — расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда ![]() (в кулонах), если
(в кулонах), если ![]() Н·м2/Кл2,
Н·м2/Кл2, ![]() Кл,
Кл, ![]() м, а
м, а ![]() Н.
Н.
13. На каком из рисунков изображено решение неравенства ![]()
В ответе укажите номер правильного варианта.
| 1)
| 2)
| ||
| 3)
| 4)
|
| |
14. В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду?
1
 5. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 47°. Найдите меньший угол между диагоналями параллелограмма. Ответ дайте в градусах.
5. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 47°. Найдите меньший угол между диагоналями параллелограмма. Ответ дайте в градусах.
1 6. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 22°. Найдите величину угла BOC. Ответ дайте в градусах.
6. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 22°. Найдите величину угла BOC. Ответ дайте в градусах.
17. В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 67. Найдите площадь треугольника ABC.
1 8. Площадь одной клетки равна 1. Найдите площадь фигуры, изображенной на рисунке.
8. Площадь одной клетки равна 1. Найдите площадь фигуры, изображенной на рисунке.
19. Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
3) Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.
4) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Решите уравнение ![]()
21. Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 час. За сколько часов наполняет бассейн одна вторая труба?
22. При каких значениях m вершины парабол ![]() и
и ![]() расположены по одну сторону от оси x?
расположены по одну сторону от оси x?
23. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8,4, а AB = 4.
24. В треугольнике ABC с тупым углом BAC проведены высоты BB1 и CC1. Докажите, что треугольники AB1C1 и ABC подобны.
25. Окружность, вписанная в треугольник ABC , касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 49°, 69° и 62°.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 16, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 17, задачи 1-25
1. В таблице даны размеры (с точностью до мм) четырех листов, имеющих форматы А0, А1, А3 и А4.
| Номер листа | Длина (мм) | Ширина (мм) |
| 1 | 297 | 210 |
| 2 | 420 | 297 |
| 3 | 1189 | 841 |
| 4 | 841 | 594 |
Установите соответствие между форматами и номерами листов. В ответ запишите последовательность четырех цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
| A0 | A1 | A3 | A4 |
|
|
|
|
|
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2.
И так далее.

Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
2. Сколько листов формата А3 получится из одного листа формата А2?
3. Найдите ширину листа бумаги формата А0. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.
4. Найдите отношение длины меньшей стороны листа формата А3 к большей. Ответ округлите до десятых.
5. Бумагу формата А5 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.
6. Найдите значение выражения
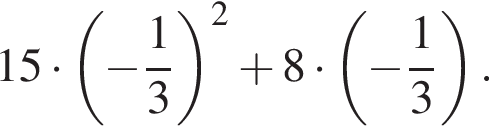
7. На координатной прямой отмечено число a. Какое из утверждений относительно этого числа является верным?
В ответе укажите номер правильного варианта.
![]()
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
8. Найдите значение выражения
![]() при
при ![]()
9. Найдите корни уравнения ![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. В магазине канцтоваров продается 264 ручки: 38 красных, 30 зеленых, 8 фиолетовых, остальные синие и черные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или черной.
11. Установите соответствие между функциями и их графиками. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам.
| 1)
| 2)
| ||||||
| 3)
| А) Б) B)
|
12. Длину окружности l можно вычислить по формуле ![]() где R — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если ее длина равна 78 м. (Считать
где R — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если ее длина равна 78 м. (Считать ![]() ).
).
13. На каком рисунке изображено множество решений неравенства ![]()
В ответе укажите номер правильного варианта.
| 1)
| 2)
|
| 3)
| 4)
|
14. При проведении химической реакции в растворе образуется нерастворимый осадок. Наблюдения показали, что каждую минуту образуется 0,5 г осадка. Найдите массу осадка (в граммах) в растворе спустя восемь минут после начала реакции.
15. Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 16, BD = 20, AB = 5. Найдите DO.

16. Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ![]() если
если ![]() Ответ дайте в градусах.
Ответ дайте в градусах.

17. В трапеции ABCD известно, что AD = 7, BC = 3, а ее площадь равна 85. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.

18. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину ее средней линии.
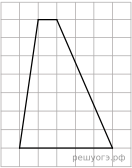
19. Какие из следующих утверждений верны?
1) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
2) В тупоугольном треугольнике все углы тупые.
3) Средняя линия трапеции равна полусумме ее оснований.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Решите неравенство ![]()
21. От пристани А к пристани В, расстояние между которыми равно 153 км, отправился с постоянной скоростью первый теплоход, а через 4 часа после этого следом за ним, со скоростью, на 16 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно.
22. Постройте график функции ![]() Определите, при каких значениях m прямая
Определите, при каких значениях m прямая ![]() имеет с графиком ровно три общие точки.
имеет с графиком ровно три общие точки.
23. В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60° , сторона AB равна 4. Найдите площадь трапеции.
24. Два квадрата имеют общую вершину. Докажите, что отмеченные на рисунке отрезки AB и CE равны.
25. В треугольнике ABC известны длины сторон AB = 15, AC = 25, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 17, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 18, задачи 1-25
1. Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета. Заполните таблицу, в бланк ответов перенесите числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответе нужно записать число 51118).
| Мобильный интернет | 2 Гб | 2,25 Гб | 4 Гб | 3,5 Гб |
| Номер месяца |
|
|
|
|
На рисунке точками показано количество минут исходящих вызовов и трафик мобильного интернета в гигабайтах, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2019 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.
В течение года абонент пользовался тарифом «Стандартный», абонентская плата по которому составляла 350 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит:
• пакет минут, включающий 300 минут исходящих вызовов на номера, зарегистрированные на территории РФ;
• пакет интернета, включающий 3 гигабайта мобильного интернета;
• пакет СМС, включающий 120 СМС в месяц;
• безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и СМС сверх пакета тарифа указана в таблице.
| Исходящие вызовы | 3 руб./мин. |
| Мобильный интернет (пакет) | 90 руб. за 0,5 Гб |
| СМС | 2 руб./шт. |
Абонент не пользовался услугами связи в роуминге. За весь год абонент отправил 110 СМС.
2. Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику израсходованных минут и гигабайтов. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам
| ПЕРИОДЫ | ХАРАКТЕРИСТИКИ | ||||
| А) март–апрель Б) апрель–май В) июнь–июль Г) июль–август | 1) Расход минут увеличился, а расход гигабайтов уменьшился. 2) Расход гигабайтов увеличился, а расход минут уменьшился. 3) Расход минут увеличился, и расход гигабайтов увеличился. 4) Расход минут уменьшился, и расход гигабайтов уменьшился. | ||||
| А | Б | В | Г |
| |
|
|
|
|
|
| |
3. Сколько рублей потратил абонент на услуги связи в июне?
4. Какой наибольший трафик мобильного интернета в гигабайтах за месяц был в 2019 году?
5. Абонент хочет приобрести новый смартфон. В трех салонах сотовой связи этот смартфон продается в кредит (сначала делается первоначальный взнос, а потом ежемесячно в течение всего срока кредита вносятся платежи) на разных условиях. Условия приведены в таблице.
| Салон | Стоимость смартфона (руб.) | Первоначальный взнос (в % от стоимости) | Срок кредита (мес.) | Ежемесячный платеж (руб.) |
| А | 18 000 | 20 | 6 | 2650 |
| Б | 17 500 | 30 | 12 | 1200 |
| В | 17 600 | 25 | 12 | 1300 |
Определите, в каком из салонов покупка обойдется дешевле всего (с учетом переплаты). В ответ запишите эту сумму в рублях.
6. Найдите значение выражения -0,2 · (−10)2+55.
7. Известно, что число m отрицательное. На каком из рисунков точки с координатами ![]() расположены на координатной прямой в правильном порядке?
расположены на координатной прямой в правильном порядке?
| 1)
| 2)
|
| 3)
| 4)
|
В ответе укажите номер правильного варианта.
8. Найдите значение выражения
![]() при
при ![]() и
и ![]()
9. Найдите корень уравнения −4 − 6x = 4x − 3.
10. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно 1 раз.
11. На одном из рисунков изображена гипербола. Укажите номер этого рисунка.
| 1) | 2) | 3) | 4) |
12. Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объем (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите температуру T (в градусах Кельвина), если ν = 68,2 моль, P = 37 782,8 Па, V = 6 м3.
13. Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.
![]()
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
14. В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 13мг. За каждые 30 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 90 минут после начала эксперимента. Ответ дайте в миллиграммах.
15. Угол A четырехугольника ABCD, вписанного в окружность, равен 56°. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
16. AC и BD — диаметры окружности с центром O. Угол ACB равен 59°. Найдите угол AOD. Ответ дайте в градусах.
17. В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 94. Найдите площадь четырехугольника ABMN.
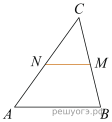
18. На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите длину его большей диагонали.
![]()
19. Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90° , то эти две прямые параллельны.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
20. Сократите дробь
![]()
21. Расстояние между городами А и В равно 120 км. Город С находится между городами А и В. Из города А в город В выехал автомобиль, а через 36 минут следом за ним со скоростью 75 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из C в А, автомобиль прибыл в В. Найдите расстояние от А до С.
22. Постройте график функции ![]() и определите, при каких значениях m прямая
и определите, при каких значениях m прямая ![]() имеет с графиком ровно три общие точки.
имеет с графиком ровно три общие точки.
23. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 3,6, а AB = 8.
24. В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BMC.
25. Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен ![]() Найдите радиус окружности, вписанной в треугольник ABC.
Найдите радиус окружности, вписанной в треугольник ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 18, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 19, задачи 1-25
1. Установите соответствие между объемами помещения и номерами печей, для которых данный объем является наибольшим для отопления помещений. Заполните таблицу, в бланк ответов перенесите последовательность трех цифр без пробелов, запятых и других дополнительных символов.
| Объем | 12 | 15 | 16 |
| Номер печи |
|
|
|
Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проема 1,8 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трех печей.
| Номер печи | Тип | Объем помещения | Масса | Стоимость |
| 1 | Дровяная | 8-12 | 40 | 18 000 |
| 2 | Дровяная | 10-16 | 48 | 19 500 |
| 3 | Электрическая | 9-15,5 | 15 | 15 000 |
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдется в 6500 руб.
2. Найдите объем парного отделения строящейся бани. Ответ дайте в кубических метрах.
3. Во сколько рублей обойдется покупка электрической печи с установкой и доставкой, если доставка печи до дачного участка будет стоить 800 рублей?
4. На дровяную печь, масса которой 48 кг, сделали скидку 10%. Сколько рублей стала стоить печь?
5. Хозяин выбрал дровяную печь (рис. 1). Чертеж передней панели печи показан на рисунке 2.

Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (см. рис. 2). Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
6. Найдите значение выражения ![]()
7. На координатной прямой отмечена точка А, которая соответствует одному из чисел, указанных ниже. Какому числу она соответствует?
![]()
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
8. Найдите значение выражения
![]() при
при ![]()
![]()
9. Найдите корни уравнения ![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. В фирме такси в данный момент свободно 15 машин: 4 черные, 3 желтые и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
11. Установите соответствие между графиками функций и формулами, которые их задают.
| А)
| Б)
| ||||||
| В)
| 1) 2) 3) 4)
|
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
12. Площадь четырехугольника можно вычислить по формуле ![]() где
где ![]() и
и ![]() — длины диагоналей четырехугольника,
— длины диагоналей четырехугольника, ![]() — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали
— угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали ![]() если
если ![]()
![]() a
a ![]()
13. Укажите решение неравенства ![]()
1)![]() 2)
2)![]()
3)![]() 4)
4)![]()
14. В амфитеатре 12 рядов. В первом ряду 18 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
15. На стороне BC прямоугольника ABCD, у которого AB = 55 и AD = 103, отмечена точка E так, что ∠EAB = 45°. Найдите ED.
16. В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 88°. Найдите вписанный угол ACB. Ответ дайте в градусах.
17. Сторона треугольника равна 29, а высота, проведенная к этой стороне, равна 12. Найдите площадь этого треугольника.

18. На клетчатой бумаге с размером клетки 1х1 изображен прямоугольный треугольник. Найдите длину его большего катета.

19. Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90° , то эти две прямые параллельны.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
20. Сократите дробь ![]()
21. Расстояние между городами А и В равно 375 км. Город С находится между городами А и В. Из города А в город В выехал автомобиль, а через 1 час 30 минут следом за ним со скоростью 75 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в В. Найдите расстояние от А до С.
22. Постройте график функции ![]() и определите, при каких значениях c прямая
и определите, при каких значениях c прямая ![]() имеет с графиком ровно три общие точки.
имеет с графиком ровно три общие точки.
23. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
24. Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
25. Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 12, тангенс угла BAC равен ![]() Найдите радиус окружности, вписанной в треугольник ABC.
Найдите радиус окружности, вписанной в треугольник ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 19, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 20, задачи 1-25
1. Пользуясь описанием, определите, какими цифрами на плане обозначены деревни. В ответ запишите последовательность четырех цифр без пробелов, запятых и других дополнительных символов.
| Деревни | Ванютино | Горюново | Егорка | Жилино |
| Цифры |
|
|
|
|
На рисунке изображен план сельской местности.
Таня на летних каникулах приезжает в гости к дедушке в деревню Антоновка (на плане обозначена цифрой 1). В конце каникул дедушка на машине собирается отвезти Таню на автобусную станцию, которая находится в деревне Богданово. Из Антоновки в Богданово можно проехать по проселочной дороге мимо реки. Есть другой путь — по шоссе до деревни Ванютино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово. Третий маршрут проходит по проселочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвертый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по проселочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Еще один маршрут проходит по шоссе до деревни Егорка, по проселочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданово.
Шоссе и проселочные дороги образуют прямоугольные треугольники.
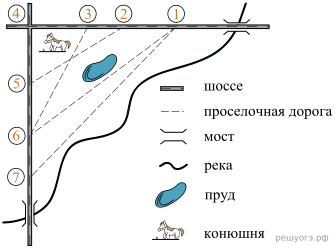
По шоссе Таня с дедушкой едут со скоростью 50 км/ч, а по проселочным дорогам — со скоростью 30 км/ч. Расстояние от Антоновки до Доломино равно 12 км, от Доломино до Егорки — 4 км, от Егорки до Ванютино — 12 км, от Горюново до Ванютино — 15 км, от Ванютино до Жилино — 9 км, а от Жилино до Богданово — 12 км.
2. Найдите расстояние от Антоновки до Егорки по шоссе. Ответ дайте в километрах.
3. Найдите расстояние от Егорки до Жилино по прямой. Ответ дайте в километрах.
4. Сколько минут затратят на дорогу Таня с дедушкой из Антоновки в Богданово, если поедут мимо пруда через Горюново?
5. За какое наименьшее количество минут Таня с дедушкой могут добраться из Егорки в Жилино?
6. Найдите значение выражения
![]()
7. На координатной прямой точками A, B, C и D отмечены числа 0,508; 0,85; -0,05; 0,058. Какой точкой изображается число 0,058?
В ответе укажите номер правильного варианта.
![]()
1) A 2) B 3) C 4) D
8. Найдите значение выражения
![]() при
при ![]()
9. Найдите корень уравнения
![]()
10. На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 8 с капустой и 3 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
11. На рисунке изображены графики функций вида ![]() Установите соответствие между знаками коэффициентов k и b и графиками функций. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам.
Установите соответствие между знаками коэффициентов k и b и графиками функций. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам.
| 1) | 3) | ||||||
| 2) | А) Б) В)
|
12. Площадь четырехугольника можно вычислить по формуле ![]() где
где ![]() и
и ![]() — длины диагоналей четырехугольника,
— длины диагоналей четырехугольника, ![]() — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали
— угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали ![]() если
если ![]()
![]() a
a ![]()
13. На каком рисунке изображено множество решений неравенства ![]()
В ответе укажите номер правильного варианта.
| 1)
| 2)
|
| 3)
| 4)
|
14. Шарами одинакового радиуса заполнили правильный треугольник, а потом тем же количеством шаров — прямоугольник. Найдите количество шаров, если известно, что и на стороне треугольника, и на большей стороне прямоугольника располагается на два шара больше, чем на меньшей стороне прямоугольника.
15. Один из острых углов прямоугольного треугольника равен 34°. Найдите его другой острый угол. Ответ дайте в градусах.
![]()
16. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA = 68°. Найдите угол NMB. Ответ дайте в градусах.

17. Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен ![]() Найдите площадь параллелограмма.
Найдите площадь параллелограмма.
18. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите ее площадь.

19. Какие из следующих утверждений верны?
1. Площадь треугольника меньше произведения двух его сторон.
2. Средняя линия трапеции равна сумме ее оснований.
3. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
20. Решите систему уравнений
21. Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором растворе?
22. Постройте график функции
![]() И определите, при каких значениях m прямая
И определите, при каких значениях m прямая ![]() имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
23. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключенная внутри этого угла, равна 100°.
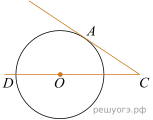
24. В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
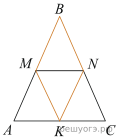
25. Диагонали четырехугольника ABCD, вершины которого расположены на окружности, пересекаются в точке M. Известно, что ![]() = 72°,
= 72°, ![]() = 102°,
= 102°, ![]() = 110°. Найдите
= 110°. Найдите ![]()
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 20, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 21, задачи 1-25
1. Завод допускает установку шин с другими маркировками. В таблице показаны разрешенные размеры шин.
| Ширина шины (мм) | Диаметр диска (дюймы) | ||
| 13 | 14 | 15 | |
| 165 | 165/70 | 165/65 | — |
| 175 | 175/65 | 175/65; 175/60 | — |
| 185 | 185/65; 185/60 | 185/60 | 185/55 |
| 195 | 195/60 | 195/55 | 195/55; 195/50 |
Шины какой наименьшей ширины можно устанавливать на автомобиль, если диаметр диска равен 15 дюймам? Ответ дайте в миллиметрах.
|
|
|
| Рис. 1 | Рис. 2 |
Автомобильное колесо, как правило, представляет собой металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведенном примере) обозначает ширину шины в миллиметрах (параметр B на рисунке 2). Второе число (число 65 в приведенном примере) — процентное отношение высоты боковины (параметр H на рисунке 2) к ширине шины, то есть ![]()
Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идет число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определенной модели и устанавливает на них колеса с шинами маркировки 165/70 R13.
2. На сколько миллиметров радиус колеса с шиной маркировки 205/55 R14 больше, чем радиус колеса с шиной маркировки 165/65 R14?
3. Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
4. На сколько миллиметров увеличится диаметр колеса, если заменить колеса, установленные на заводе, колесами с шинами маркировки
195/50 R15?
5. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колеса, установленные на заводе, колесами с шинами маркировки 175/60 R14? Результат округлите до десятых.
6. Найдите значение выражения
![]()
7. Сравните числа x и y, если
![]()
![]() В ответ запишите значение меньшего из чисел.
В ответ запишите значение меньшего из чисел.
8. Найдите значение выражения
![]() при
при ![]()
9. Решите уравнение ![]()
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
10. Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет менее 4 очков.
11. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
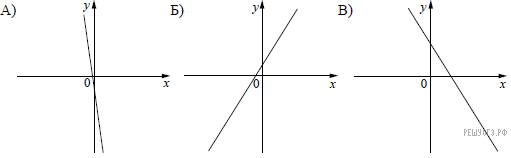
| 1) k 0, b | 2) k |
| ||||||
| 3) k 0 | 4) k 0, b 0 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам.
12. В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C = 6000 + 4100 · n , где n — число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 7 колец.
13. Решите неравенство ![]() и определите, на каком рисунке изображено множество его решений.
и определите, на каком рисунке изображено множество его решений.
В ответе укажите номер правильного варианта.
| 1)
| 2)
| |||
|
| 3)
| 4)
|
| |
14. В амфитеатре 14 рядов. В первом ряду 20 мест, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько мест в десятом ряду амфитеатра?
15. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 60° и 55°. Найдите меньший угол параллелограмма.

16. AC и BD — диаметры окружности с центром O. Угол ACB равен 70°. Найдите угол AOD. Ответ дайте в градусах.

17. Сторона треугольника равна 14, а высота, проведенная к этой стороне, равна 31. Найдите площадь этого треугольника.

18. Найдите тангенс угла А треугольника ABC, изображенного на рисунке.

19. Какие из следующих утверждений верны?
1) Существуют три прямые, которые проходят через одну точку.
2) Боковые стороны любой трапеции равны.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Решите систему уравнений 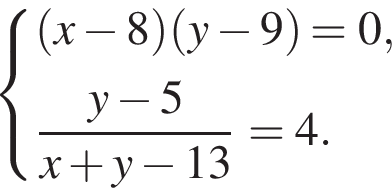
21. Три бригады вместе изготовили 114 карданных валов. Известно, что вторая бригада изготовила карданных валов в 3 раза больше, чем первая, и на 16 карданных валов меньше, чем третья. На сколько карданных валов больше изготовила третья бригада, чем первая?
22. Постройте график функции ![]() Определите, при каких значениях m прямая
Определите, при каких значениях m прямая ![]() имеет с графиком ровно три общие точки.
имеет с графиком ровно три общие точки.
23. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 7,5, а AB = 2.
24. Внутри параллелограмма ABCD выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади параллелограмма.
25. Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в ее середине. Найдите диаметр описанной окружности треугольника ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 21, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 22, задачи 1-25
1. Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета. Заполните таблицу, в бланк ответов перенесите числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответе нужно записать число 51118).
| Мобильный интернет | 2,5 Гб | 3 Гб | 3,25 Гб | 1 Гб |
| Номер месяца |
|
|
|
|
На рисунке точками показано количество минут исходящих вызовов и трафик мобильного интернета в гигабайтах, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2019 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.

В течение года абонент пользовался тарифом «Стандартный», абонентская плата по которому составляла 350 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит:
• пакет минут, включающий 300 минут исходящих вызовов на номера, зарегистрированные на территории РФ;
• пакет интернета, включающий 3 гигабайта мобильного интернета;
• пакет СМС, включающий 120 СМС в месяц;
• безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и СМС сверх пакета тарифа указана в таблице.
| Исходящие вызовы | 3 руб./мин. |
| Мобильный интернет (пакет) | 90 руб. за 0,5 Гб |
| СМС | 2 руб./шт. |
Абонент не пользовался услугами связи в роуминге. За весь год абонент отправил 110 СМС.
2. Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику израсходованных минут и гигабайтов.
| ПЕРИОДЫ | ХАРАКТЕРИСТИКИ |
| А) январь− февраль Б) февраль− март В) август–сентябрь Г) ноябрь– декабрь | 1) Расход минут увеличился, а расход гигабайтов уменьшился. 2) Расход гигабайтов увеличился, а расход минут уменьшился. 3) Расход минут увеличился, и расход гигабайтов увеличился. 4) Расход минут уменьшился, и расход гигабайтов уменьшился. |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
|
|
|
|
|
3. Сколько рублей потратил абонент на услуги связи в июне?
4. Какое наименьшее количество минут исходящих вызовов за месяц было в 2019 году?
5. Абонент хочет приобрести новый смартфон. В трех салонах сотовой связи этот смартфон продается в кредит (сначала делается первоначальный взнос, а потом ежемесячно в течение всего срока кредита вносятся платежи) на разных условиях. Условия приведены в таблице.
| Салон | Стоимость смартфона (руб.) | Первоначальный взнос (в % от стоимости) | Срок кредита (мес.) | Ежемесячный платеж (руб.) |
| А | 18 000 | 20 | 6 | 2650 |
| Б | 17 500 | 30 | 12 | 1200 |
| В | 17 600 | 25 | 12 | 1300 |
Определите, в каком из салонов покупка обойдется дешевле всего (с учетом переплаты). В ответ запишите эту сумму в рублях.
6. Найдите значение выражения
![]()
7. Известно, что число m отрицательное. На каком из рисунков точки с координатами ![]() расположены на координатной прямой в правильном порядке?
расположены на координатной прямой в правильном порядке?
| 1)
| 2)
|
| 3)
| 4)
|
В ответе укажите номер правильного варианта.
8. Найдите значение выражения ![]()
9. Решите уравнение ![]()
10. Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 4 или 7.
11. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c. В таблице под каждой буквой укажите соответствующий номер.
| 1)
| 2)
| ||||||
| 3)
| А) Б) В)
|
12. Полную механическую энергию тела (в джоулях) можно вычислить по формуле ![]() где m — масса тела (в килограммах), υ — его скорость (в м/с), h — высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а g — ускорение свободного падения (в м/с2). Пользуясь этой формулой, найдите m (в килограммах), если
где m — масса тела (в килограммах), υ — его скорость (в м/с), h — высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а g — ускорение свободного падения (в м/с2). Пользуясь этой формулой, найдите m (в килограммах), если ![]()
![]()
![]() а
а ![]()
13. На каком рисунке изображено множество решений неравенства ![]()
В ответе укажите номер правильного варианта.
| 1)
| 2)
|
| 3)
| 4)
|
14. Лене надо подписать 972 открытки. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Лена подписала 20 открыток. Определите, сколько открыток было подписано за седьмой день, если вся работа была выполнена за 18 дней.
1 5. В треугольнике ABC известно, что
5. В треугольнике ABC известно, что ![]() AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
1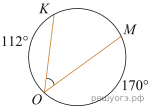 6. Найдите ∠KOM, если градусные меры дуг KO и OM равны 112° и 170° соответственно.
6. Найдите ∠KOM, если градусные меры дуг KO и OM равны 112° и 170° соответственно.
1 7. Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, угол сектора равен 120°, а радиус круга равен 9. В ответе укажите площадь, деленную на π.
7. Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, угол сектора равен 120°, а радиус круга равен 9. В ответе укажите площадь, деленную на π.
18. Найдите тангенс угла AOB, изображенного на рисунке.
19. Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна 180° , то эти прямые параллельны.
3) Площадь треугольника не превышает произведения двух его сторон.
20. Решите уравнение ![]()
21. Два велосипедиста одновременно отправляются в 180-километровый пробег. Первый едет со скоростью на 5 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.
22. Постройте график функции
![]()
и определите, при каких значениях m прямая ![]() имеет с графиком ровно две общие точки.
имеет с графиком ровно две общие точки.
23. Высота AH ромба ABCD делит сторону CD на отрезки DH = 24 и CH = 6. Найдите высоту ромба.
2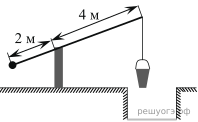 4. Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников AEB и CED равна половине площади параллелограмма.
4. Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников AEB и CED равна половине площади параллелограмма.
25. На рисунке изображен колодец с «журавлем». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 22, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 23, задачи 1-25
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населенные пункты. В ответ запишите полученную последовательность пяти цифр.
| Насел. пункты | п. Демидово | д. Ключи | ст. Таировка | с. Федяево | д. Царево |
| Цифры |
|
|
|
|
|
Юля летом отдыхает у дедушки и бабушки в деревне Царево. Юля с дедушкой собираются съездить на машине на железнодорожную станцию Таировку. Из Царево в Таировку можно проехать по шоссе до деревни Ключи, где нужно свернуть под прямым углом налево на другое шоссе, ведущее в Таировку через поселок Демидово. Из Царево в Таировку можно проехать через поселок Демидово и не заезжая в Ключи, но тогда первую часть пути надо будет ехать по прямой лесной дороге. Есть и третий маршрут: доехать по прямой грунтовой дороге мимо озера до села Федяево и там, повернув направо, по шоссе добраться до Таировки.
По шоссе Юля с дедушкой едут со скоростью 60 км/ч, а по лесной и грунтовой дорогам — 45 км/ч. Расстояние по шоссе от Царево до Ключей равно 72 км, от Таировки до Ключей — 60 км, от Таировки до Демидово — 30 км, а от Таировки до Федяево — 27 км.
2. Найдите расстояние от деревни Царево до поселка Демидово по лесной дороге. Ответ дайте в километрах.
3. Сколько минут затратят на дорогу Юля с дедушкой, если поедут на станцию через Ключи?
4. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Юля с дедушкой, если поедут этим маршрутом.
5. На шоссе машина дедушки расходует 6,5 литра бензина на 100 км. Известно, что на путь из Царево до Таировки через Ключи и на путь через Федяево ей необходим один и тот же объем бензина. Сколько литров бензина на 100 км машина дедушки расходует на грунтовых дорогах?
6. Найдите значение выражения 9,3 + 7,8.
7. На координатной прямой отмечено число a.
![]()
Найдите наименьшее из чисел a2, a3, a4.
В ответе укажите номер правильного варианта.
1) a2 2) a3 3) a4
4) не хватает данных для ответа
8. Найдите значение выражения
![]() при
при ![]() и
и ![]()
9. Решите уравнение ![]()
10. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Норвегии или Швеции.
11. Установите соответствие между функциями и их графиками. В таблице под каждой буквой укажите соответствующий номер.
| 1)
| 2)
| ||||||
| 3)
| А) Б) B)
|
12. Площадь четырехугольника можно вычислить по формуле ![]() где
где ![]() и
и ![]() — длины диагоналей четырехугольника,
— длины диагоналей четырехугольника, ![]() — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали
— угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали ![]() если
если ![]()
![]() a
a ![]()
13. Решите неравенство ![]()
В ответе укажите номер правильного варианта.
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
14. При хранении бревен их укладывают, как показано на рисунке. Сколько бревен находится в одной кладке, если в ее основании положено 12 бревен?

15. Радиус окружности с центром в точке O равен 97, длина хорды AB равна 130 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.

16. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB Найдите угол ACB, если угол AOB равен 73°. Ответ дайте в градусах

17. Найдите площадь трапеции, изображенной на рисунке.
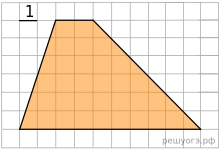
18. На клетчатой бумаге с размером клетки 1×1 отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC.

19. Какие из следующих утверждений верны?
1. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
2. В тупоугольном треугольнике все углы тупые.
3. Средняя линия трапеции равна полусумме ее оснований.
20. Найдите значение выражения ![]() если
если ![]()
21. Найдите целое число a, если из двух следующих утверждений верно только одно: 1) ![]() 2)
2) ![]()
22. При каких значениях p вершины парабол ![]() и
и![]() расположены по разные стороны от оси x?
расположены по разные стороны от оси x?
23. Высота AH ромба ABCD делит сторону CD на отрезки DH = 24 и CH = 6. Найдите высоту ромба.
24. В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
25. Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Найдите радиус окружности, вписанной в треугольник ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 23, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 24, задачи 1-25
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырех цифр.
| Объекты | Банк | Магазин | Дом, где живетТаня | Квартал старыхдомов |
| Цифры |
|
|
|
|
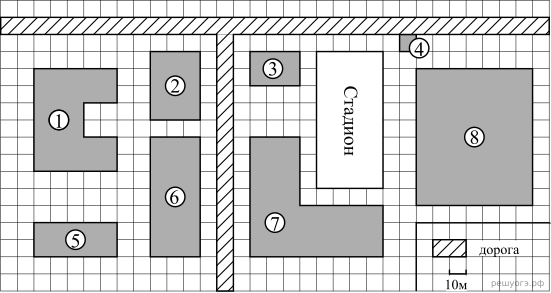
На плане (см. рис.) изображен район города, в котором живет Петя. Сторона каждой клетки на плане равна 10 м.
Дом, в котором живет Петя, обозначен цифрой 6. Прямо напротив дома, где живет Петя, через дорогу находится дом в форме буквы «Г», где живет его друг Вася. Рядом с домом, где живет Петя, расположен дом, где живет одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м2. А с другой стороны дома, где живет Таня, расположен детский сад. Недалеко от детского сада и дома, где живет Петя, находится магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от нее — квартал старых одноэтажных домов.
2. Территорию стадиона необходимо засеять газонной травой. В одной упаковке газонной травы содержится 12 кг семян, при этом для засеивания 3 м2 земли необходимо 100 г семян. Какое минимальное количество упаковок газонной травы необходимо приобрести?
3. Найдите суммарную площадь, которую занимают дома, где проживают Таня, Петя и Вася. Ответ дайте в м2.
4. Найдите расстояние от дома, где живет Петя, до автобусной остановки (расстояние между двумя ближайшими точками по прямой) в метрах.
5. Компания выбирает место для строительства торгово‐развлекательного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м2 площади комплекса. Стоимость земли, цена строительства комплекса с учетом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.
| Место | Цена земли (млн руб.) | Цена строительства (млн руб.) | Длина коммуникаций (м) | Стоимость аренды за 1 м2 (руб./месяц) |
| Центр | 64,4 | 176 | 200 | 1200 |
| Окраина | 11,2 | 168 | 3500 | 900 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.
6. Найдите значение выражения ![]()
7. Значение какого из данных выражений положительно, если известно, что ![]()
1) ![]() ; 2)
; 2) ![]() ; 3) xy; 4)
; 3) xy; 4) ![]()
8. Найдите значение выражения
![]() при a = 6.
при a = 6.
9. Решите уравнение ![]()
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. Средний рост жителя города, в котором живет Даша, равен 170 см. Рост Даши 173 см. Какое из следующих утверждений верно?
1) Даша — самая высокая девушка в городе.
2) Обязательно найдется девушка ниже 170 см.
3) Обязательно найдется человек ростом менее 171 см.
4) Обязательно найдется человек ростом 167 см.
11. На рисунках изображены графики функций вида ![]() Установите соответствие между знаками коэффициентов k и b и графиками функций. В таблице под каждой буквой укажите соответствующий номер.
Установите соответствие между знаками коэффициентов k и b и графиками функций. В таблице под каждой буквой укажите соответствующий номер.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам.
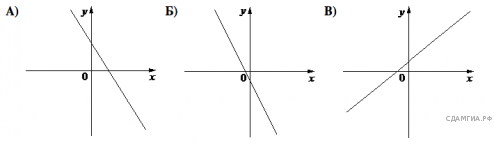
| 1) 2) 3) |
|
12. Площадь трапеции ![]() можно вычислить по формуле
можно вычислить по формуле
![]() где
где ![]() — основания трапеции, h — высота (в метрах). Пользуясь этой формулой, найдите высоту h, если основания трапеции равны
— основания трапеции, h — высота (в метрах). Пользуясь этой формулой, найдите высоту h, если основания трапеции равны ![]() и
и ![]() а ее площадь
а ее площадь ![]()
13. Решите систему неравенств
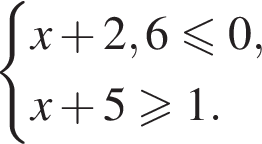
На каком рисунке изображено множество ее решений?
| 1)
| 2)
|
| 3)
| 4)
|
1) 1; 2) 2; 3) 3; 4) 4
14. Бизнесмен Бубликов получил в 2000 году прибыль в размере 5000 рублей. Каждый следующий год его прибыль увеличивалась на 300% по сравнению с предыдущим годом. Сколько рублей заработал Бубликов за 2003 год?
15. Тангенс острого угла прямоугольной трапеции равен ![]() Найдите ее большее основание, если меньшее основание равно высоте и равно 8.
Найдите ее большее основание, если меньшее основание равно высоте и равно 8.

16. Радиус окружности, описанной около квадрата, равен ![]() Найдите длину стороны этого квадрата.
Найдите длину стороны этого квадрата.

17. Два катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого треугольника.

18. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.

19. Какие из следующих утверждений верны?
1) Если противоположные углы выпуклого четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
2) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.
3) Сумма двух противоположных углов четырехугольника не превосходит 180°.
4) Если основания трапеции равны 4 и 6, то средняя линия этой трапеции равна 10.
20. Решите неравенство ![]()
21. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 130 литров она заполняет на 4 минуты быстрее, чем первая труба заполняет резервуар объемом 136 литров?
22. Постройте график функции
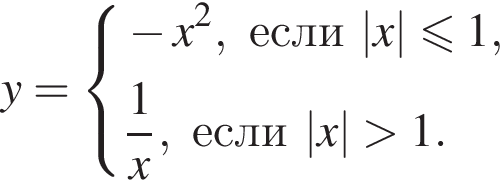
и определите, при каких значениях c прямая ![]() будет иметь с графиком единственную общую точку.
будет иметь с графиком единственную общую точку.
23. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 16. Найдите ее среднюю линию.
24. В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK = BN. Докажите, что данный параллелограмм — прямоугольник.
25. В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 14, BC = 7.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 24, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 25, задачи 1-25
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырех цифр.
| Объекты | Сцена | Туалеты | Детская площадка | Кафе |
| Цифры |
|
|
|
|
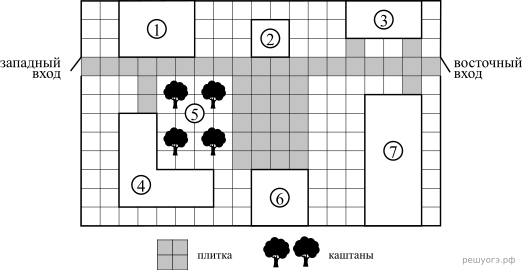
На плане (см. рис.) изображен парк культуры и отдыха города Малый. Сторона каждой клетки равна 2 м. Парк имеет прямоугольную форму. Зайти в парк можно через один из двух входов: западный или восточный.
Если зайти в парк через западный вход, то слева будет расположено кафе «Полдник», а справа — детская площадка. Рядом с детской площадкой посажены каштаны. Рядом с восточным входом располагаются общественные туалеты и бадминтонная площадка, обозначенная на плане цифрой 7. Помимо указанных объектов, в парке имеются фонтан (отмечен цифрой 2) и сцена. Все дорожки в парке имеют ширину 2 м и вымощены тротуарной плиткой 1 м × 1 м. Между фонтаном и сценой имеется площадка, вымощенная такой же плиткой.
2. Тротуарная плитка продается в упаковках по 10 штук. Сколько упаковок плитки понадобилось купить, чтобы выложить все дорожки и площадку между сценой и фонтаном?
3. Найдите площадь (в м2), которую занимает бадминтонная площадка.
4. Детскую площадку планируется огородить заборчиком. Найдите длину этого заборчика в метрах.
5. Для остекления витрин кафе «Полдник» требуется заказать 30 одинаковых стекол в одной из трех фирм. Площадь каждого стекла 0,7 м2. В таблице приведены цены на стекло и на резку стекла. Сколько рублей будет стоить самый дешевый заказ?
| Фирма | Цена стекла (руб./м2) | Резка стекла (руб./шт.) | Дополнительные условия |
| «Вени» | 560 | 35 | — |
| «Види» | 570 | 24 | При заказе на сумму свыше 15 000 рублей резка бесплатна |
| «Вици» | 600 | 13 | При заказе на сумму свыше 12 500 рублей резка бесплатна |
6. Найдите значение выражения ![]()
7. Одна из точек, отмеченных на координатной прямой, соответствует числу ![]() Какая это точка?
Какая это точка?
![]()
1) точка A; 2) точка B
3) точка C; 4) точка D
8. Найдите значение выражения
![]() при x = 36.
при x = 36.
9. Решите уравнение
![]()
10. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
11. Установите соответствие между графиками функций и формулами, которые их задают. Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
|
А) |
В) | ||||||
|
Б) | 1) 2) 3)
|
12. Центростремительное ускорение при движении по окружности (в м/с2) можно вычислить по формуле a = ω2R, где ω — угловая скорость (в с −1), а R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с−1, а центростремительное ускорение равно 289 м/с2.
13. Укажите решение системы неравенств
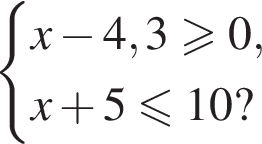
| 1)
| 2)
|
| 3)
| 4)
|
14. Давление воздуха под колоколом равно 625 мм ртутного столба. Каждую минуту насос откачивает из-под колокола 20% находящегося там воздуха. Определите давление (в мм рт. ст.) через 5 минут после начала работы насоса.
15. Радиус окружности с центром в точке O равен 97, длина хорды AB равна 130 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.

16. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 13. Найдите AC, если ![]()

17. Высота BH ромба ABCD делит его сторону AD на отрезки ![]() и
и ![]() Найдите площадь ромба.
Найдите площадь ромба.

18. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

19. Укажите номера верных утверждений.
1) Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны.
2) Сумма смежных углов равна 180°.
3) Любая высота равнобедренного треугольника является его биссектрисой.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Решите систему уравнений
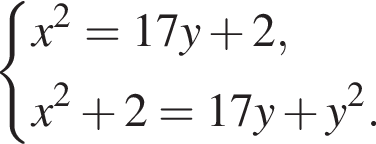
21. Имеются два сосуда, содержащие 30 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 40 % кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 37 % кислоты. Сколько процентов кислоты содержится во втором растворе?
22. Постройте график функции
![]() Определите, при каких значениях m прямая
Определите, при каких значениях m прямая ![]() имеет с графиком ровно три общие точки.
имеет с графиком ровно три общие точки.
23. В треугольнике ABC угол С равен 90°, радиус вписанной окружности равен 2. Найдите площадь треугольника ABC, если AB = 12.
24. В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA = MB. Докажите, что данный параллелограмм — прямоугольник.
25. Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 9:7. Найдите отношение площади треугольника ABK к площади четырехугольника KPCM.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 25, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 26, задачи 1-25
1. В таблице даны размеры (с точностью до мм) четырех листов, имеющих форматы А0, А1, А3 и А4.
| Номер листа | Длина (мм) | Ширина (мм) |
| 1 | 297 | 210 |
| 2 | 420 | 297 |
| 3 | 1189 | 841 |
| 4 | 841 | 594 |
Установите соответствие между форматами и номерами листов. В ответ запишите последовательность четырех цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
| A0 | A1 | A3 | A4 |
|
|
|
|
|
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2.
И так далее.

Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
2. Сколько листов формата А3 получится из одного листа формата А2?
3. Найдите площадь листа формата А1. Ответ дайте в квадратных сантиметрах.
4. Найдите отношение длины меньшей стороны листа формата А3 к большей. Ответ округлите до десятых.
5. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот же текст, напечатанный шрифтом высотой 15 пунктов на листе формата А4? Размер шрифта округляется до целого.
6. Вычислите:
![]()
7. Одна из точек, отмеченных на координатной прямой, соответствует числу ![]() Какая это точка?
Какая это точка?
![]()
1) точка M; 2) точка N
3) точка P; 4) точка Q
8. Найдите значение выражения ![]()
9. Решите уравнение:
![]()
10. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
11. Установите соответствие между графиками функций и формулами, которые их задают. Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
| А)
| Б)
| ||||||
| В)
| 1) 2) 3) 4)
|
12. Площадь четырехугольника можно вычислить по формуле
![]() где
где ![]() и
и ![]() — длины диагоналей четырехугольника,
— длины диагоналей четырехугольника, ![]() — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали
— угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали ![]() если
если
![]()
![]() a
a ![]()
13. На каком рисунке изображено множество решений системы неравенств
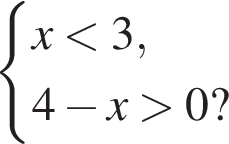
В ответе укажите номер правильного варианта.
| 1)
| 2)
|
| 3)
| 4)
|
14. Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 9 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые пять секунд?
15. В треугольнике ABC угол C равен 90°, AC = 3,
tgA = ![]() Найдите AB.
Найдите AB.
16. Касательные в точках A и B к окружности с центром O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в градусах.
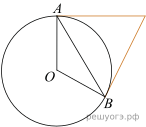
17. Найдите площадь трапеции, изображенной на рисунке.
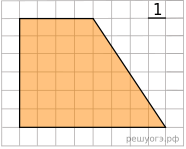
18. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.

19. Укажите номера верных утверждений.
1) Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны.
2) Сумма смежных углов равна 180°.
3) Любая высота равнобедренного треугольника является его биссектрисой.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Упростите выражение
![]()
21. При смешивании первого раствора соли, концентрация которого 40%, и второго раствора этой же соли, концентрация которого 65%, получили раствор, содержащий 60% соли. В каком отношении были взяты первый и второй растворы?
22. Постройте график функции ![]() и определите, при каких значениях c прямая
и определите, при каких значениях c прямая ![]() имеет с графиком ровно три общие точки.
имеет с графиком ровно три общие точки.
23. Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
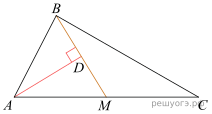
24. В параллелограмме ABCD точка M — середина стороны CD. Известно, что MA = MB. Докажите, что данный параллелограмм — прямоугольник.
25. Две касающиеся внешним образом в точке K окружности, радиусы которых равны 33 и 39, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 26, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 27, задачи 1-25
1. Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счет гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.
|
|
|
|
|
|
2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведенная к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ![]() (рис. 2). Ответ дайте в сантиметрах.
(рис. 2). Ответ дайте в сантиметрах.
4. Вася нашел площадь купола зонта как площадь поверхности сферического сегмента по формуле ![]() где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число
где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число ![]() округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учетом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
6. Запишите десятичную дробь, равную сумме
![]()
7. На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.
![]()
Какое из следующих утверждений относительно этих чисел является верным?
1) a30; 2) a − b 0; 3) ab a + b 1
8. Найдите значение выражения
![]()
При ![]()
9. Решите уравнение
![]()
10. В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке.
11. На рисунке изображены графики функций вида y = ax2 + bx + c. Для каждого графика укажите соответствующие ему значения коэффициента a и дискриминанта D.
| А)
| Б)
| 1) a 0, D 0 2) a 0, D 3) a D 0 4) a D
| ||||||||
| В)
| Г)
| Запишите в ответ цифры, расположив их в порядке, соответствующем буквам |
12. Площадь четырехугольника можно вычислить по формуле
![]() где
где ![]() и
и ![]() — длины диагоналей четырехугольника,
— длины диагоналей четырехугольника, ![]() — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали
— угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали ![]() если
если ![]()
![]() a
a ![]()
13. Решите неравенство
![]()
1) [-8;8]; 2) ![]()
3) нет решений; 4) ![]()
14. Однажды богач заключил выгодную, как ему казалось, сделку с человеком, который в течение 15 дней ежедневно должен был приносить по 1000 р., а взамен в первый день богач должен был отдать 10 р., во второй — 20 р., в третий — 40 р., в четвертый — 80 р. и т. д. в течение 15 дней. Сколько денег получил богач и сколько он отдал? Кто выиграл от этой сделки? В ответ запишите, сколько рублей потерял богач за 15 дней.
15. Медиана равностороннего треугольника равна ![]() Найдите сторону этого треугольника.
Найдите сторону этого треугольника.
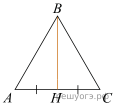
16. В треугольнике ABC угол C равен 90°, AC = 30 , BC = ![]() Найдите радиус окружности, описанной около этого треугольника.
Найдите радиус окружности, описанной около этого треугольника.

17. Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
18. На клетчатой бумаге с размером клетки 1x1 изображен прямоугольный треугольник. Найдите длину его большего катета.
19. Какие из следующих утверждений верны?
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
2) Если угол равен 60°, то смежный с ним равен 120°.
3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.
4) Через любые три точки проходит не более одной прямой.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Упростите выражение:
![]()
21. Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12 вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?
22. При каких значениях m вершины парабол
![]() и
и ![]() расположены по одну сторону от оси x?
расположены по одну сторону от оси x?
23. В треугольнике ABC угол С равен 90°, радиус вписанной окружности равен 3. Найдите площадь треугольника ABC, если AB = 15.
24. Биссектрисы углов C и D трапеции ABCD пересекаются в точке P, лежащей на стороне AB. Докажите, что точка P равноудалена от прямых BC, CD и AD.
25. Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 27, задачи 1-25
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 28, задачи 1-25
1. Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета.
Заполните таблицу, в бланк ответов перенесите числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответе нужно записать число 51118).
| Мобильный интернет | 3 Гб | 3,75 Гб | 4 Гб | 1,5 Гб |
| Номер месяца |
|
|
|
|
На рисунке точками показано количество минут исходящих вызовов и трафик мобильного интернета в гигабайтах, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2019 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.

В течение года абонент пользовался тарифом «Стандартный», абонентская плата по которому составляла 350 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит:
• пакет минут, включающий 300 минут исходящих вызовов на номера, зарегистрированные на территории РФ;
• пакет интернета, включающий 3 гигабайта мобильного интернета;
• пакет СМС, включающий 120 СМС в месяц;
• безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и СМС сверх пакета тарифа указана в таблице.
| Исходящие вызовы | 3 руб./мин. |
| Мобильный интернет (пакет) | 90 руб. за 0,5 Гб |
| СМС | 2 руб./шт. |
Абонент не пользовался услугами связи в роуминге. За весь год абонент отправил 110 СМС.
2. Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику израсходованных минут и гигабайтов.
| ПЕРИОДЫ | ХАРАКТЕРИСТИКИ |
| А) март–апрель Б) апрель–май В) июнь–июль Г) июль–август | 1) Расход минут увеличился, а расход гигабайтов уменьшился. 2) Расход гигабайтов увеличился, а расход минут уменьшился. 3) Расход минут увеличился, и расход гигабайтов увеличился. 4) Расход минут уменьшился, и расход гигабайтов уменьшился. |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
|
|
|
|
|
3. Сколько рублей потратил абонент на услуги связи в июле?
4. Какой наибольший трафик мобильного интернета в гигабайтах за месяц был в 2019 году?
5. Абонент хочет приобрести новый смартфон. В трех салонах сотовой связи этот смартфон продается в кредит (сначала делается первоначальный взнос, а потом ежемесячно в течение всего срока кредита вносятся платежи) на разных условиях. Условия приведены в таблице.
| Салон | Стоимость смартфона (руб.) | Первоначальный взнос (в % от стоимости) | Срок кредита (мес.) | Ежемесячный платеж (руб.) |
| А | 17 000 | 25 | 12 | 1250 |
| Б | 16 600 | 30 | 12 | 1200 |
| В | 17 500 | 20 | 6 | 2600 |
Определите, в каком из салонов покупка обойдется дешевле всего (с учетом переплаты). В ответ запишите эту сумму в рублях.
6. Найдите значение выражения
![]()
7. Известно, что ![]() Какое из указанных утверждений неверно?
Какое из указанных утверждений неверно?
1) ![]() ; 2)
; 2) ![]()
3) ![]() ; 4)
; 4) ![]()
8. Найдите значение выражения
![]() при
при ![]()
9. Решите систему уравнений
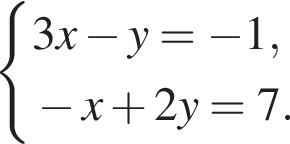 В ответ запишите х + у.
В ответ запишите х + у.
10. Коля наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 3.
11. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c. В таблице под каждой буквой укажите соответствующий номер.
| А)
| Б)
| ||||||
| В)
| 1) 2) 3)
|
12. Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F) пользуются формулой ![]() где
где ![]() — градусы Цельсия, F — градусы Фаренгейта. Какая температура (в градусах) по шкале Фаренгейта соответствует 20° по шкале Цельсия?
— градусы Цельсия, F — градусы Фаренгейта. Какая температура (в градусах) по шкале Фаренгейта соответствует 20° по шкале Цельсия?
13. Укажите решение системы неравенств
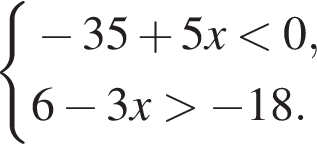
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]()
14. В первый день больной заражает четырех человек, каждый из которых на следующий день заражает новых четырех и так далее. На второй день больной изолируется и больше уже никого не заражает. Болезнь длится 14 дней. В первый день месяца в город N приехал заболевший гражданин К, и в этот же день он заразил четырех человек. В какой день станет 1365 заболевших? (В ответе укажите только число.)

 15. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 11° и 63° соответственно. Ответ дайте в градусах.
15. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 11° и 63° соответственно. Ответ дайте в градусах.
16. На отрезке AB выбрана точка C так, что ![]() и
и ![]() Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведенной из точки B к этой окружности.
Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведенной из точки B к этой окружности.
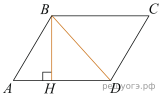
 17. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 5 и HD = 15. Диагональ параллелограмма BD равна 17. Найдите площадь параллелограмма.
17. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 5 и HD = 15. Диагональ параллелограмма BD равна 17. Найдите площадь параллелограмма.
18. Найдите тангенс угла AOB, изображенного на рисунке.
19. Какие из следующих утверждений верны?
1) Около любого правильного многоугольника можно описать не более одной окружности.
2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.
3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.
4) Около любого ромба можно описать окружность.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Решите систему уравнений
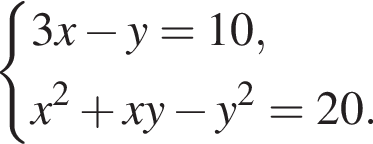
21. Имеются два сосуда, содержащие 24 кг и 26 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 39% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится в первом растворе?
22. Постройте график функции
![]() Определите, при каких значениях m прямая
Определите, при каких значениях m прямая ![]() имеет с графиком ровно три общие точки.
имеет с графиком ровно три общие точки.
23. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8, а AB = 3.
24. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник.
25. Стороны AC, AB, BC треугольника ABC равны ![]()
![]() и 2 соответственно. Точка K расположена вне треугольника ABC, причем отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному.
и 2 соответственно. Точка K расположена вне треугольника ABC, причем отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному.
Найдите косинус угла AKC, если ∠KAC90° .
ОГЭ 2024 МАТЕМАТИКА 9 класс Вариант 28, задачи 1-25
Ответы
Данное издание – книга для учащихся, не содержит ответов.
Книга для учителя содержит ответы. Издание с ответами можно запросить у составителя данного учебного пособия.
Контакты:
e-mail: [email protected]
ВК: https://vk.com/makolan
__________________________________________________________________________________________________________________________________________
Репетитор по математике, тел: +7967-470-21-77 ВК: https://vk.com/makolan