23.11.2020г.
Математика
6 а/б класс. Ссылка на видеоурок https://youtu.be/qT5qXlDDd-s
Тема урока: Числовые промежутки. Понятие множества, элемента множества, подмножества. Пересечение и объединение множеств. Графическая и аналитическая модель числовых промежутков.
Открой тетрадь и запиши число на полях и «Классная работа».
Ниже запиши тему урока.
Запишите в тетрадь все определения, таблицу и примеры.
Числовые промежутки или просто промежутки — множества всех чисел, удовлетворяющих неравенству. По другому, это числовые множества, которые можно изобразить на координатной прямой.
Числовые промежутки – луч и открытый луч
Сегодня на уроке мы познакомимся с понятиями «луч», «открытый луч», «отрезок», «интервал», «числовые промежутки», а также научимся записывать по рисунку числовые промежутки и неравенства.

Для рассмотрения новых понятий воспользуемся рисунками, на которых изображена координатная прямая. Правда, без обозначенных на ней начала отсчета и единичного отрезка. Мы это сделали для того, чтобы не загромождать рисунок.
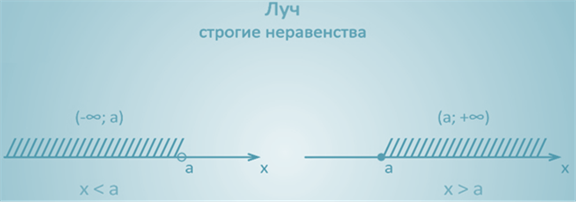
На координатной прямой отмечена точка a, штриховкой отмечены все точки прямой, которые лежат правее a,т.е. числа большие числаa.
Такое множество точек (чисел) называют открытым лучом и обозначают так:
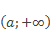
Читают так: а плюс бесконечность или от а до плюс бесконечности.
Для любого числа х из этого множества верно неравенство х a.
Таким образом, открытый луч – это луч, начало которого ему не принадлежит.
Строгие и нестрогие неравенства

Рассмотрим еще один открытый луч:
На координатной прямой штриховкой отмечены точки, которые расположены слева от точки а. Эти числа меньше, чем а.
Данное множество точек (чисел) обозначается так:
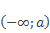
И читается: от минус бесконечности до а.
Для любого числа х этого открытого луча верно неравенство
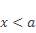

Обратите внимание, на рисунках, которые мы рассмотрели, точка, соответствующая числу а, обозначена незакрашенным кружочком.
Если закрасить кружок, то множество чисел изменится.
В этом случае число, обозначающее точку а, тоже принадлежит к заштрихованному множеству. Получается луч.
Данные множества записываются с помощью квадратной скобки:
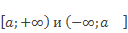
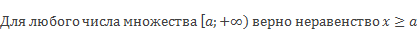
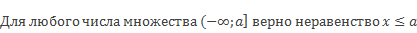
Такие неравенства называют нестрогими.
Неравенства вида х a и х строгими.
Числовые промежутки – интервал и отрезок
Рассмотрим еще два рисунка.
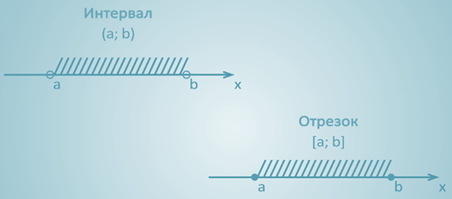
На обоих рисунках штриховкой обозначены точки (числа), которые находятся между точками a и b. В первом случае числа a и b не входят в множество – точки не закрашены, во втором входят – точки закрашены.
Первое множество называют интервалом и обозначают с помощью круглых скобок (a; b).
На втором рисунке изображен тот же интервал, но к нему присоединили его концы точки а и b, поэтому это уже не интервал, а отрезок, и записывается данное множество с помощью квадратных скобок [а; b].
Для всех точек интервала (a; b) верно двойное неравенство а
Для всех точек х, принадлежащих отрезку [а; b], верно двойное нестрогое неравенство а ≤ х ≤ b, (х больше или равен а, но меньше или равен b).
Запись числового промежутка и неравенства по рисунку
«Луч», «открытый луч», «отрезок», «интервал» – это всё числовые промежутки.
Часто при решении задачи мы рисуем схему по ее условию, а затем составляем уравнение. И схема и уравнение – это математические модели ситуации, описанной в задаче.
Схема – графическая модель, уравнение – аналитическая модель.
Аналогично дело обстоит и с числовыми промежутками.
Числовой промежуток – это все числа, соответствующие определенному условию.
Условие соответствует какой-либо математической ситуации. Можно построить как графическую, так и аналитическую модель, кроме того сделать еще и символическую запись.
Например, все числа меньшие 3.
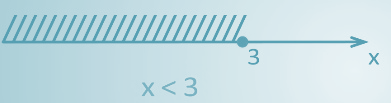
В данном случае числовым промежутком будет открытый луч, графическая модель будет такая:
Аналитической моделью является строгое неравенство х а символическая запись (-∞; 3).
Графическими моделями для числовых промежутков являются: луч, открытый луч, отрезок, интервал.
Аналитическими моделями: строгие, нестрогие неравенства, а так же двойные неравенства.
Обобщим полученную знания о числовых промежутках в следующей таблице.
Виды числовых промежутков:
(перерисуйте в тетрадь данную таблицу) 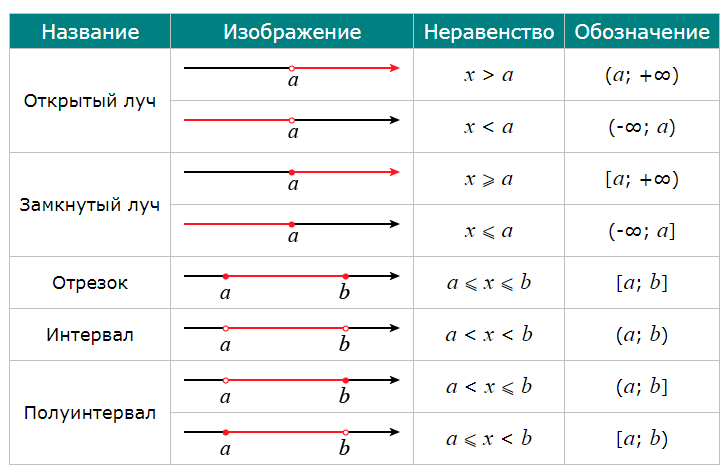
В таблице a и b — это граничные точки, а x — переменная, которая может принимать координату любой точки, принадлежащей числовому промежутку.
Граничная точка — это точка, определяющая границу числового промежутка. Граничная точка может как принадлежать числовому промежутку, так и не принадлежать ему. На чертежах граничные точки, не принадлежащие рассматриваемому числовому промежутку, обозначают незакрашенным кругом, а принадлежащие — закрашенным кругом.
Сделай паузу. Выполни упражнения:

Теперь рассмотрим на конкретных примерах виды числовых промежутков.
Открытый луч
Рассмотрим множество точек координатной прямой, имеющих координату, большую 2, а, значит, расположенных правее точки 2:
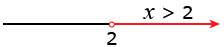
Такое множество можно задать неравенством x 2. Открытые лучи обозначаются с помощью круглых скобок — (2; +∞), данная запись читается так: открытый числовой луч от двух до плюс бесконечности.
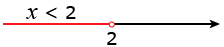
Множество, которому соответствует неравенство x
Замкнутый луч
Замкнутые числовые лучи задаются нестрогими неравенствами. Например, неравенства x ⩾ 2 и x ⩽ 2 можно изобразить так:
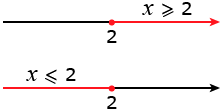
Обозначаются данные замкнутые лучи так: [2; +∞) и (-∞; 2], читается это так: числовой луч от двух до плюс бесконечности и числовой луч от минус бесконечности до двух. Квадратная скобка в обозначении показывает, что точка 2 принадлежит числовому промежутку.
Отрезок
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:

Множество точек, из которых состоит данный отрезок, можно задать двойным неравенством -2 ⩽ x ⩽ 3 или обозначить [-2; 3], такая запись читается так: отрезок от минус двух до трёх.
Интервал и полуинтервал
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:

Множество точек, из которых состоит данный интервал, можно задать двойным неравенством -2 x
Полуинтервал — это множество точек прямой, лежащих между двумя граничными точками, одна из которых принадлежит множеству, а другая не принадлежит. Такие множества задаются двойными неравенствами:
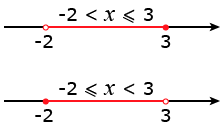
Обозначаются данные полуинтервалы так: (-2; 3] и [-2; 3). Читается это так: полуинтервал от минус двух до трёх, включая 3, и полуинтервал от минус двух до трёх, включая минус два.
Теперь рассмотрим, какие операции можно производить с числовыми промежутками.
Пересечение и объединение числовых промежутков
Пересечение числовых промежутков
Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают А∩В. Промежуток [3;5] является пересечением промежутков [-1;5] и [3;7]. Это можно записать так: [-1;5]∩[3;7]=[3;5].

Промежутки [0;4] и [6;10] не имеют общих элементов. Если множество не имеет общих элементов, то говорят, что их пересечение пусто. Значит, пересечение промежутков [0;4]∩[6;10]=0.

Объединение числовых промежутков
Каждое число из промежутка [1;7] принадлежит хотя бы одному из промежутков [1;5] и [3;7], то есть, либо промежутку [1;5], либо промежутку [3;7], либо им обоим.
Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают A B.
B.
Промежуток [1;7] является объединением промежутков [1;5] и [3;7]. Это можно записать так:
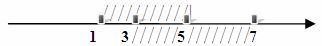
Заметим, что объединение промежутков не всегда представляет собой промежуток, например множество не является промежутком.

Теперь подведи итоги своей работе на уроке и устно ответь на вопросы:
Что такое числовой промежуток?
Какими скобками обозначается строгое неравенство?
Что называют пересечением множеств А∩В?
Что называют объединением множеств A B?
B?
Сделай в тетради все необходимы записи, разбери еще раз непонятные для тебя моменты, отдохни 15 минут.
Теперь открой файл «23.11.20 Практикум Числовые промежутки», рассмотри примеры решенных заданий, выполни упражнения самостоятельно, пришли на проверку свою работу.





















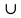 B.
B.









