Вариант № 6
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответе запишите полученную последовательность четырёх цифр.
| Населённые пункты | Кулаки | Илькино | Осинки | Кудрино |
| Цифры |
|
|
|
|
Гена летом отдыхает у дедушки в деревне Осинки. В воскресенье они собираются съездить на машине в село Кудрино. Из деревни Осинки в Кудрино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Илькино до деревни Кулаки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Кудрино. Есть и третий маршрут: в Илькине можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Кудрино.
По шоссе Гена с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 40 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 2 км.
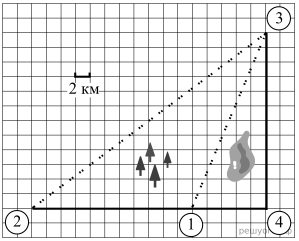
Решение. Пользуясь описанием и рисунком можно заметить, что деревня Кулаки соответствует цифре 4, деревня Илькино — цифре 1, деревня Осинки — цифре 2 и деревня Кудрино —цифре 3.
Ответ: 4123.
2. Найдите расстояние от деревни Осинки до села Кудрино по прямой. Ответ выразите в километрах.
Решение. Расстояние от деревни Осинки до села Кудрино соответствует длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора имеем:

Ответ: 40.
3. Сколько километров проедут Гена с дедушкой, если они поедут по шоссе через деревню Кулаки?
Решение. Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Ответ: 56.
4. Сколько времени затратят на дорогу Гена с дедушкой, если они поедут сначала до Илькино, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
Решение. По шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно, они затратят 22 : 60 = 0,37 часа или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по теореме Пифагора длина составит:
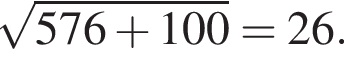
По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч, следовательно, они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61 минута.
Ответ: 61.
5. Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Гена с дедушкой, если поедут этим маршрутом.
Решение. Гена с дедушкой могут поехать тремя разными маршрутами. Рассмотрим каждый из них.
1) По грунтовой дороге напрямую. Длина такого пути соответствует длине гипотенузы прямоугольного треугольника с катетами 32 и 24. По теореме Пифагора имеем:

Двигаясь по грунтовой дороге со скоростью 40 км/ч дедушка с Геной потратят 40 : 40 = 1 час или 60 минут.
2) Сначала по шоссе, а затем по грунтовой дороге вдоль озера. По шоссе Гена с дедушкой проедут 22 километра со скоростью 60 км/ч. Следовательно, они затратят 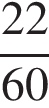 часа или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по теореме Пифагора длина составит:
часа или 22 минуты. Дальше по условию задачи они свернут на грунтовую дорогу длина которой равна длине гипотенузы прямоугольного треугольника с катетами 24 и 10. Таким образом, по теореме Пифагора длина составит:
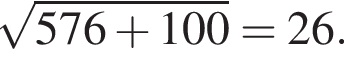
По грунтовой дороге Гена с дедушкой едут со скоростью 40 км/ч, следовательно, они затратят 26 : 40 = 0,65 часа или 39 минут.
Таким образом, Гена с дедушкой на весь путь затратят 22 + 39 = 61 минута.
3) По шоссе через Кулаки. Расстояние, которое проедут Гена с дедушкой, проезжая через Кулаки, равно сумме длин катетов прямоугольного треугольника с катетами 32 и 24. Таким образом, имеем, что искомое расстояние равно 32 + 24 = 56.
Двигаясь по шоссе со скоростью 60 км/ч, Гена с дедушкой потратят  часа или 56 минут.
часа или 56 минут.
Таким образом, самый быстрый путь составит 56 минут.
Ответ: 56.
6. Найдите значение выражения 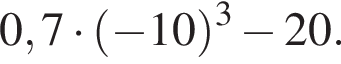
Решение. Последовательно получаем:
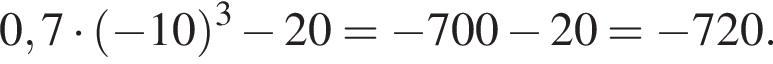
Ответ: −720.
7. Известно, что 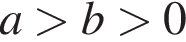 . Какое из указанных утверждений верно?
. Какое из указанных утверждений верно?
В ответе укажите номер правильного варианта.
1) 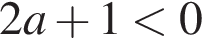
2) 
3) 
4) 
Решение. По условию оба числа положительны и  Рассмотрим все варианты ответа:
Рассмотрим все варианты ответа:
1) 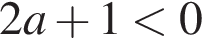 — неверно, так как
— неверно, так как 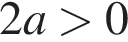 и
и 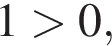
2) 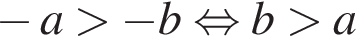 — неверно, так как по условию
— неверно, так как по условию 
3)  — неверно, так как по условию
— неверно, так как по условию 
4)  — верно.
— верно.
Правильный ответ указан под номером 4.
8. Найдите значение выражения 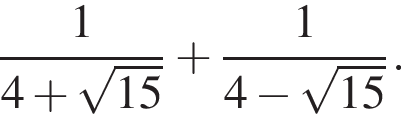
Решение. Вычислим:
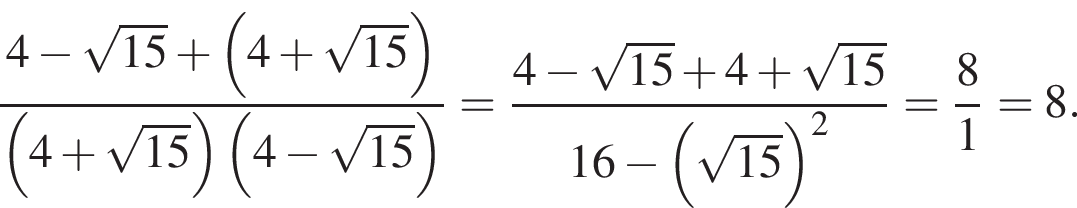
Ответ: 8.
9. Решите уравнение: x2 − 25 = 0.
Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Решение. Решим уравнение:
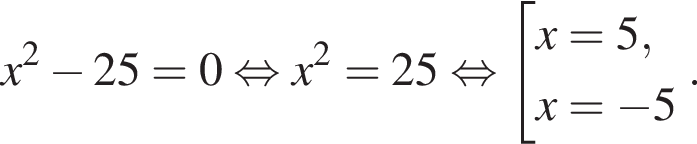
Ответ: 5.
10. У бабушки 15 чашек: 9 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Решение. Вероятность того, что чай нальют в чашку с синими цветами равна отношению количества чашек с синими цветами к общему количеству чашек. Всего чашек с синими цветами: 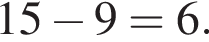 Поэтому искомая вероятность
Поэтому искомая вероятность 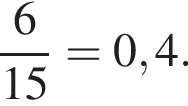
Ответ: 0,4.
11. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
КОЭФФИЦИЕНТЫ
А) 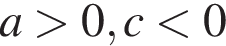
Б) 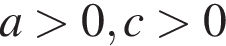
В) 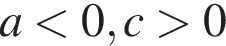
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
Решение. Если парабола задана уравнением 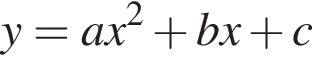 , то: при
, то: при  то ветви параболы направлены вверх, а при
то ветви параболы направлены вверх, а при  — вниз. Значение c соответствует значению функции в точке x = 0. Следовательно, если график пересекает ось ординат выше оси абсцисс, то значение c положительно, если ниже оси абсцисс — отрицательно.
— вниз. Значение c соответствует значению функции в точке x = 0. Следовательно, если график пересекает ось ординат выше оси абсцисс, то значение c положительно, если ниже оси абсцисс — отрицательно.
Таким образом, функциям соответствуют следующие графики: А — 1, Б — 2, В — 3.
Ответ: 123.
12. Площадь треугольника можно вычислить по формуле 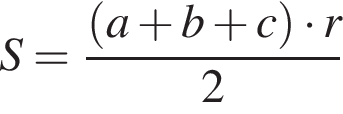 , где
, где 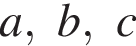 — длины сторон треугольника, r — радиус вписанной окружности. Вычислите длину стороны c, если
— длины сторон треугольника, r — радиус вписанной окружности. Вычислите длину стороны c, если 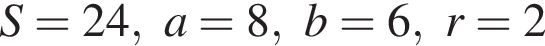 .
.
Решение. Подставим в формулу известные значения величин:
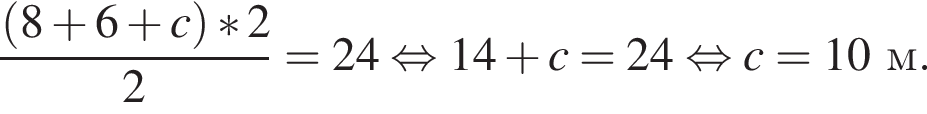
Ответ: 10.
13. Укажите решение неравенства 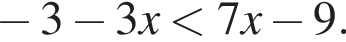
1) 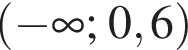
2) 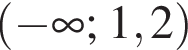
3) 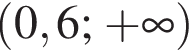
4) 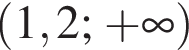
Решение. Решим неравенство:

Решению неравенства соответствует третий вариант ответа.
Правильный ответ указан под номером 3.
14. Три конькобежца, скорости которых в некотором порядке образуют геометрическую прогрессию, одновременно стартуют (из одного места) по кругу. Через некоторое время второй конькобежец обгоняет первого, пробежав на 400 метров больше его. Третий конькобежец пробегает то расстояние, который пробежал первый к моменту обгона его вторым, за время на  мин больше, чем первый. Найдите скорость первого конькобежца в м/мин.
мин больше, чем первый. Найдите скорость первого конькобежца в м/мин.
Решение. Из условия видно, что скорость 2-го конькобежца наибольшая, а 3-го — наименьшая. Обозначим за b скорость третьего конькобежца.
|
| скорость (м/мин) |
| 1-й конькобежец | qb |
| 2-й конькобежец | q2b |
| 3-й конькобежец | b |
Где q 1, b 0, t — время, за которое второй обгоняет первого.
Составим систему уравнений:

Разделим (1) на (2): 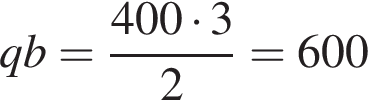 м/мин — скорость первого конькобежца.
м/мин — скорость первого конькобежца.
Ответ: 600 м/мин.
15.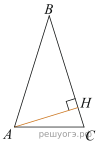
В треугольнике ABC AB = BC, а высота AH делит сторону BC на отрезки BH = 45 и CH = 30. Найдите cosB.
Решение. Из треугольника ABH, по определению косинуса:
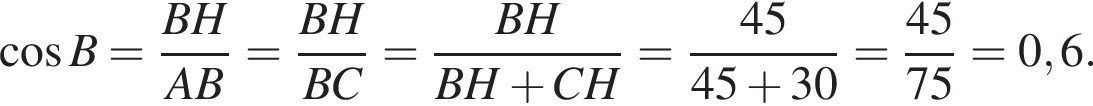
Ответ: 0,6.
16. 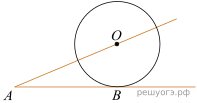 К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 8 , AO = 10 .
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 8 , AO = 10 .
Решение. Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в точку касания, поэтому OB перпендикулярен AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB: по теореме Пифагора равен 6 см.
Ответ: 6.
17.  Сторона равностороннего треугольника равна 10. Найдите его площадь, делённую на
Сторона равностороннего треугольника равна 10. Найдите его площадь, делённую на  .
.
Решение. Площадь треугольника равна половине произведения сторон на синус угла между ними. Так как угол равностороннего треугольника равен 60° и все стороны равны 10, имеем:
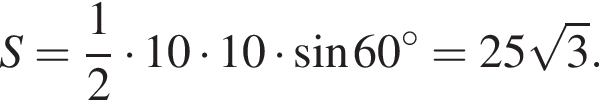
Ответ: 25.
18. 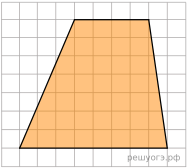 На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.
Решение. 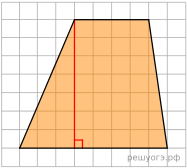 Площадь трапеции равна произведению полусуммы оснований на высоту. Таким образом,
Площадь трапеции равна произведению полусуммы оснований на высоту. Таким образом,
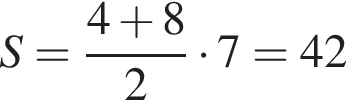
Ответ: 42
19. Какие из следующих утверждений верны?
1. Площадь треугольника меньше произведения двух его сторон.
2. Средняя линия трапеции равна сумме её оснований.
3. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Решение. Рассмотрим каждое из утверждений:
1. Площадь треугольника меньше произведения двух его сторон - верно, согласно формуле для площади треугольника: 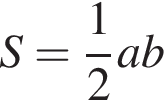
2. Средняя линия трапеции равна сумме её оснований - неверно, средняя линия трапеция равна полусумме её оснований
3. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны - верно, согласно признаку подобия треугольников.
Ответ: 13
20. Решите систему уравнений 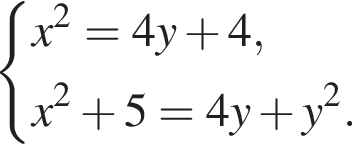
Решение. Последовательно получаем:
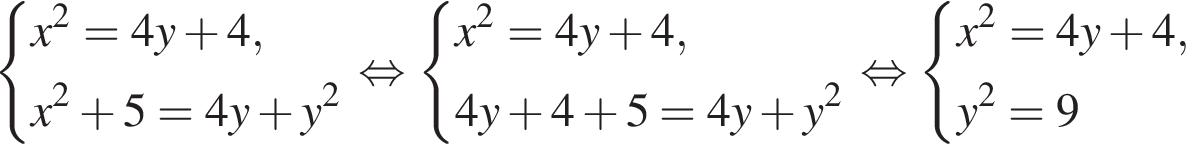
При y = −3 первое уравнение не имеет решений. При y = 3 получаем:
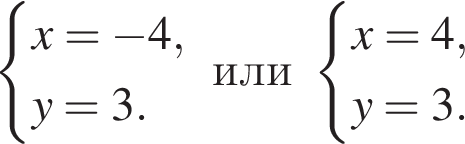
Ответ: (−4; 3); (4; 3).
21. Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Решение. Пусть скорость второго велосипедиста равна  ,
,  тогда скорость первого велосипедиста равна
тогда скорость первого велосипедиста равна 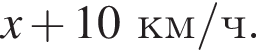 Составим таблицу по данным задачи:
Составим таблицу по данным задачи:
|
| Скорость, км/ч | Время, ч | Расстояние, км |
| Первый велосипедист | 
| 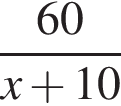
| 60 |
| Второй велосипедист | x | 
| 60 |
Так как первый прибыл к финишу на 3 ч. раньше второго, то можно составить следующее уравнение:
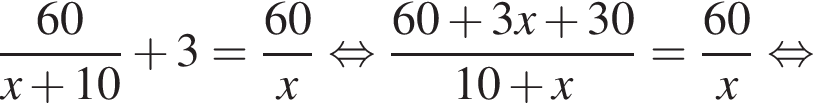

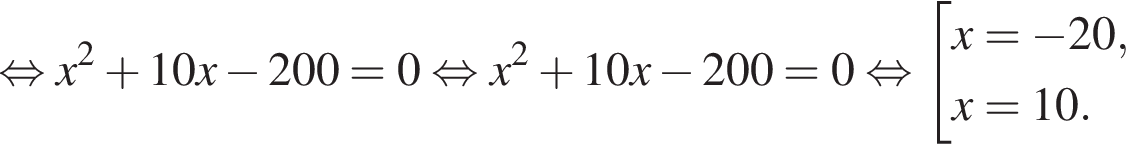
По условию задачи нам подходят только положительные корни, поэтому скорость второго велосипедиста равна 
Ответ: 10.
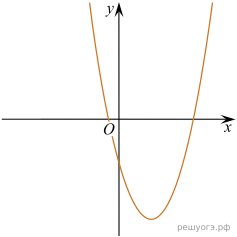
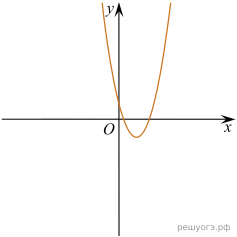
22. При каком значении р прямая 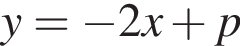 имеет с параболой
имеет с параболой 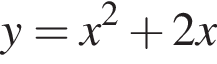 ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении
ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении 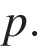
Решение. Найдём абсциссы точек пересечения:
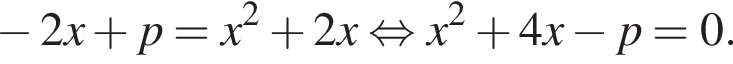
Графики функций, будут иметь ровно одну точку пересечения, если это уравнение имеет ровно одно решение. То есть, если дискриминант этого квадратного уравнения будет равен нулю.
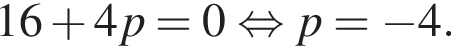
Подставив параметр p в уравнение, найдём x координату точки пересечения этих функций:
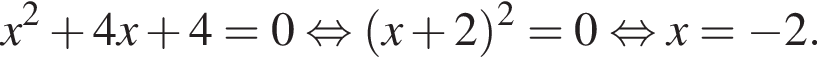
Координата y находится путём подстановки координаты x в любое из уравнений, например, в первое:
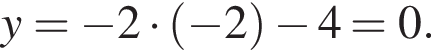
Теперь, зная p, можем построить графики обеих функций (см. рис.).
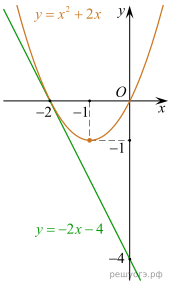
Ответ: p = −4; координаты искомой точки: (−2; 0).
23.  Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140°.
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140°.
Решение.  Проведём радиус OA. Треугольник AOC — прямоугольный, ∠A = 90°. ∠COA = 180° − ∠AOD = 180° − 140° = 40°; ∠ACO = 90° − 40° = 50°.
Проведём радиус OA. Треугольник AOC — прямоугольный, ∠A = 90°. ∠COA = 180° − ∠AOD = 180° − 140° = 40°; ∠ACO = 90° − 40° = 50°.
Ответ: 50.
24.  В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рис.). Докажите, что ВFDЕ — параллелограмм.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рис.). Докажите, что ВFDЕ — параллелограмм.
Решение.  Прямоугольные треугольники ABE и CDF равны по гипотенузе и острому углу (AB = CD как противолежащие стороны параллелограмма; ∠BAE = ∠DCF как накрест лежащие углы при параллельных прямых AB и CD и секущей AC). Следовательно, BE = DF. Кроме того, BE || DF, т. к. это перпендикуляры к одной прямой. Таким образом, в четырёхугольнике BFDE противолежащие стороны равны и параллельны, поэтому BFDE — параллелограмм.
Прямоугольные треугольники ABE и CDF равны по гипотенузе и острому углу (AB = CD как противолежащие стороны параллелограмма; ∠BAE = ∠DCF как накрест лежащие углы при параллельных прямых AB и CD и секущей AC). Следовательно, BE = DF. Кроме того, BE || DF, т. к. это перпендикуляры к одной прямой. Таким образом, в четырёхугольнике BFDE противолежащие стороны равны и параллельны, поэтому BFDE — параллелограмм.
25. В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD = 15 , BC = 14.
Решение.  Пусть T — точка пересечения прямых AB и CD, P — проекция точки E на прямую CD, Q — проекция точки C на прямую AD (см. рис.). Обозначим ∠CDA = α, CD = x.
Пусть T — точка пересечения прямых AB и CD, P — проекция точки E на прямую CD, Q — проекция точки C на прямую AD (см. рис.). Обозначим ∠CDA = α, CD = x.
Поскольку QD = AD − AQ = AD − BC = 1, получаем, что 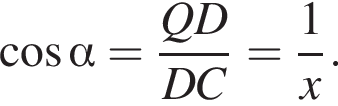
Из подобия треугольников TBC и TAD находим, что TC = 14x.
Поэтому
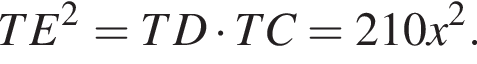
Следовательно,
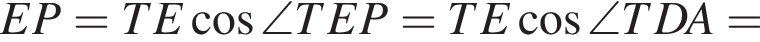
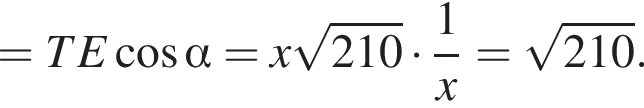
Ответ: 
| № задания | ответ |
| 1 | 4123 |
| 2 | 40 |
| 3 | 56 |
| 4 | 61 |
| 5 | 56 |
| 6 | −720 |
| 7 | 4 |
| 8 | 8 |
| 9 | 5 |
| 10 | 0,4 |
| 11 | 123 |
| 12 | 10 |
| 13 | 3 |
| 14 | 600 |
| 15 | 0,6 |
| 16 | 6 |
| 17 | 25 |
| 18 | 42 |
| 19 | 13 |
| 20 | (−4; 3); (4; 3). |
| 21 | 10 |
| 22 | p = −4; координаты искомой точки: (−2; 0). |
| 23 | 50 |
| 24 | - |
| 25 | 
|








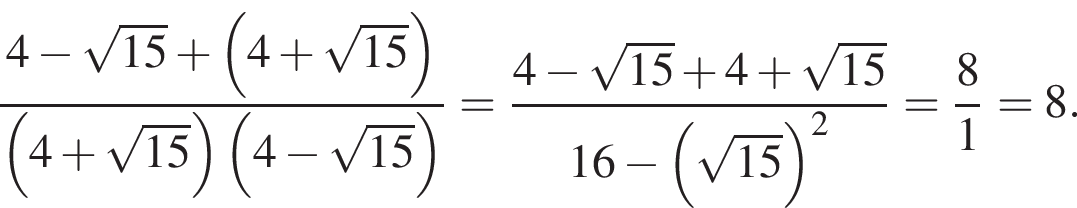



 К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 8 , AO = 10 .
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 8 , AO = 10 . Сторона равностороннего треугольника равна 10. Найдите его площадь, делённую на
Сторона равностороннего треугольника равна 10. Найдите его площадь, делённую на  На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь. Площадь трапеции равна произведению полусуммы оснований на высоту. Таким образом,
Площадь трапеции равна произведению полусуммы оснований на высоту. Таким образом,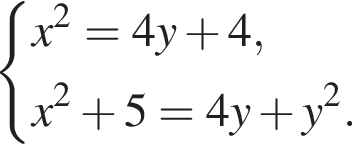
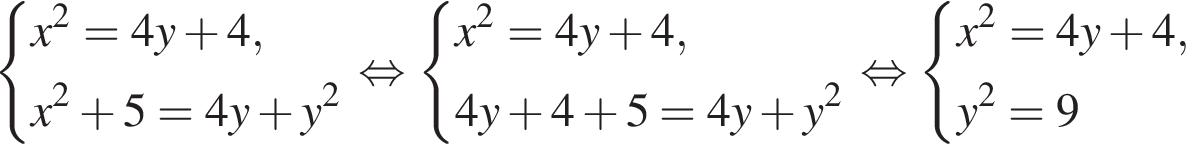
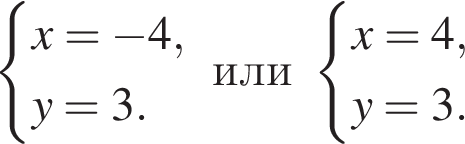
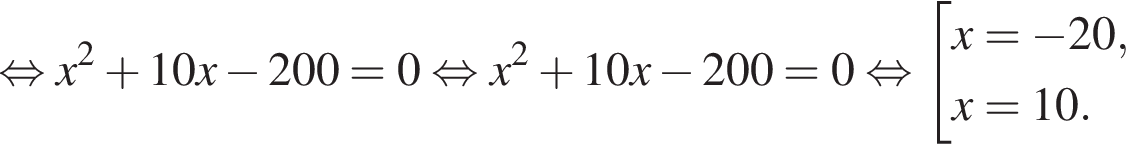

 Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140°.
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140°. Проведём радиус OA. Треугольник AOC — прямоугольный, ∠A = 90°. ∠COA = 180° − ∠AOD = 180° − 140° = 40°; ∠ACO = 90° − 40° = 50°.
Проведём радиус OA. Треугольник AOC — прямоугольный, ∠A = 90°. ∠COA = 180° − ∠AOD = 180° − 140° = 40°; ∠ACO = 90° − 40° = 50°. В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рис.). Докажите, что ВFDЕ — параллелограмм.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рис.). Докажите, что ВFDЕ — параллелограмм. Прямоугольные треугольники ABE и CDF равны по гипотенузе и острому углу (AB = CD как противолежащие стороны параллелограмма; ∠BAE = ∠DCF как накрест лежащие углы при параллельных прямых AB и CD и секущей AC). Следовательно, BE = DF. Кроме того, BE || DF, т. к. это перпендикуляры к одной прямой. Таким образом, в четырёхугольнике BFDE противолежащие стороны равны и параллельны, поэтому BFDE — параллелограмм.
Прямоугольные треугольники ABE и CDF равны по гипотенузе и острому углу (AB = CD как противолежащие стороны параллелограмма; ∠BAE = ∠DCF как накрест лежащие углы при параллельных прямых AB и CD и секущей AC). Следовательно, BE = DF. Кроме того, BE || DF, т. к. это перпендикуляры к одной прямой. Таким образом, в четырёхугольнике BFDE противолежащие стороны равны и параллельны, поэтому BFDE — параллелограмм. Пусть T — точка пересечения прямых AB и CD, P — проекция точки E на прямую CD, Q — проекция точки C на прямую AD (см. рис.). Обозначим ∠CDA = α, CD = x.
Пусть T — точка пересечения прямых AB и CD, P — проекция точки E на прямую CD, Q — проекция точки C на прямую AD (см. рис.). Обозначим ∠CDA = α, CD = x.









