Вариант № 7
1. Найдите объём парного отделения строящейся бани (в куб. м).
Хозяин дачного участка строит баню с парным отделением. Размеры парного отделения: длина — 4 м, ширина — 2,4 м, высота — 2 м. Для разогрева парного помещения можно использовать электрическую или дровяную печь. Три возможных варианта даны в таблице.
| Номер печи | Тип | Объем помещения | Масса | Стоимость |
| 1 | Дровяная | 10-15 | 45 | 21 300 |
| 2 | Дровяная | 14-21 | 51 | 24 100 |
| 3 | Электрическая | 13-20 | 17 | 18 500 |
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 6600 руб. Кроме того, хозяин подсчитал, что за год электрическая печь израсходует 2500 киловатт-часов электроэнергии по 3,5 руб. за 1 киловатт-час, а дровяная печь за год израсходует 1,8 куб. м дров, которые обойдутся по 1600 руб. за 1 куб. м.
Решение. Объем парного отделения может быть вычислен по формуле: 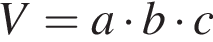 , где a — ширина, b — длина, с — высота. Имеем:
, где a — ширина, b — длина, с — высота. Имеем: 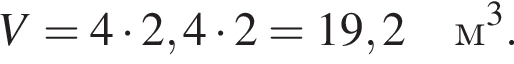
Ответ: 19,2.
2. На сколько рублей дровяная печь, подходящая по отапливаемому объёму парного отделения, обойдётся дешевле электрической с учётом установки?
Решение. Стоимость дровяной печи составит 24 100 рублей.
Вычислим во сколько обойдется электрическая печь с учетом установки: 18 500 + 6600 = 25 100.
Таким образом, дровяная печь обойдется на 1000 рублей дешевле.
Ответ: 1000.
3. На сколько рублей эксплуатация дровяной печи обойдётся дешевле эксплуатации электрической в течение года?
Решение. За год эксплуатации электрическая печь потребует: 2500 · 3,5 = 8750 рублей.
За год эксплуатации дровяная печь потребует: 1600 · 1,8 = 2880 рублей.
Таким образом, эксплуатация дровяной печи будет дешевле эксплуатации электрической на 8750 − 2880 = 5870 рублей.
Ответ: 5870.
4. Доставка печи из магазина до участка стоит 600 рублей. При покупке печи ценой выше 20 000 рублей магазин предлагает скидку 5% на товар и 30% на доставку. Сколько будет стоить покупка печи номер 2 вместе с доставкой на этих условиях?
Решение. Вычислим стоимость покупки печи номер 2:
(24 100 − 0,05 · 24 100) + (600 − 600 · 0,3) = 22 895 + 420 = 23 315.
Ответ: 23 315.
5. Хозяин выбрал дровяную печь. Чертёж печи показан на рис. 1.
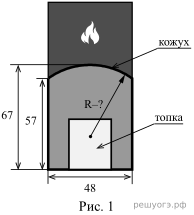
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке по дуге окружности (см. рис. 1). Для установки печки хозяину понадобилось узнать радиус закругления арки R. Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус в сантиметрах.
Решение.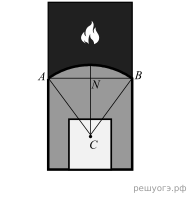
Введем обозначения как показано на рисунке. Треугольник ABC является равнобедренным. В этом треугольнике CN является биссектрисой медианой и высотой, таким образом, треугольник CNB — прямоугольный.
Имеем:
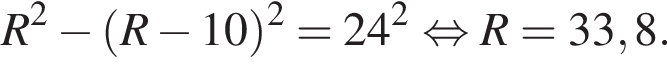
Ответ: 33,8.
6. Найдите значение выражения 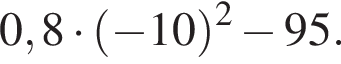
Решение. Последовательно получаем:
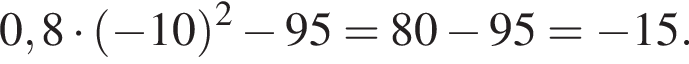
Ответ: −15.
7. На координатной прямой изображены числа a и c. Какое из следующих неравенств неверно?

1) 
2) 
3) 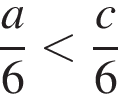
4) 
Решение. Заметим, что  Проверим все варианты ответа:
Проверим все варианты ответа:
1)  — верно,
— верно,
2) 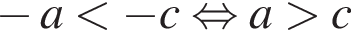 — верно,
— верно,
3) 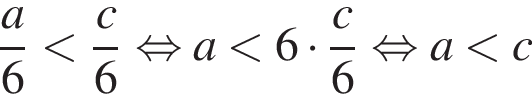 — неверно,
— неверно,
4) 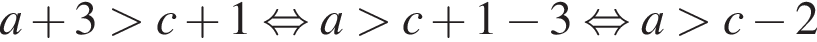 — верно.
— верно.
Неверным является неравенство 3.
8. Найдите значение выражения 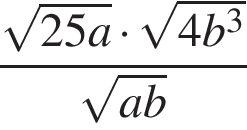 при a = 7 и b = 11.
при a = 7 и b = 11.
Решение. Упростим выражение:
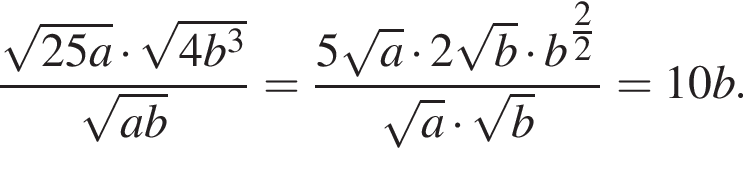
При b = 11 значение полученного выражения равно 10 · 11 = 110.
Ответ: 110.
9. Найдите корни уравнения 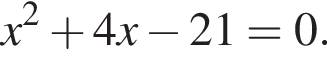
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение. По теореме, обратной теореме Виета, сумма корней равна −4, а их произведение равно −21. Тем самым, это числа −7 и 3.
Ответ: −73.
10. Девятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру. Найдите вероятность того, что начинать игру должна будет девочка.
Решение. Из пятерых детей — девочек трое. Поэтому вероятность равна 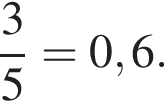
Ответ: 0,6.
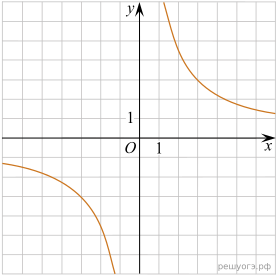
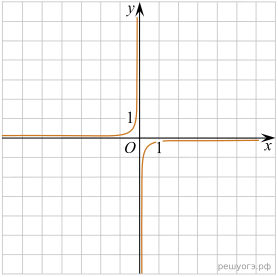
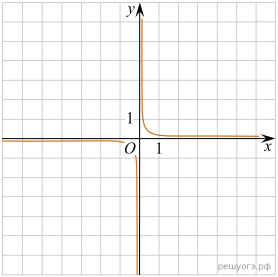
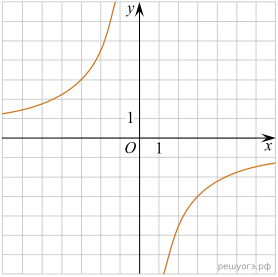
11. Установите соответствие между функциями и их графиками.
Графики
Функции
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Решение. Все представленные здесь функции — гиперболы. Общая формула для уравнения гиперболы: 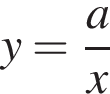 , если
, если  , то ветви гиперболы располагаются в первой и третьей четвертях, в противном случае — во второй и четвёртой четвертях.
, то ветви гиперболы располагаются в первой и третьей четвертях, в противном случае — во второй и четвёртой четвертях.
Для того, чтобы отличить гиперболы лежащие в одинаковых четвертях нужно подставить какое-нибудь значение x в формулу и проверить, какому графику будет соответствовать полученное значение.
Таким образом, установим соответсвие: А — 4, Б — 1, В — 3.
Ответ: 413.
12. Закон Джоуля–Ленца можно записать в виде Q = I2Rt, где Q — количество теплоты (в джоулях), I — сила тока (в амперах), R — сопротивление цепи (в омах), а t — время (в секундах). Пользуясь этой формулой, найдите время t (в секундах), если Q = 27 Дж, I = 1,5 A, R = 2 Ом.
Решение. Выразим время из формулы Джоуля-Ленца: 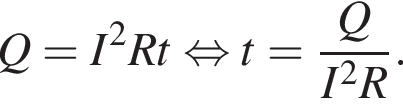 Подставляя, находим:
Подставляя, находим:
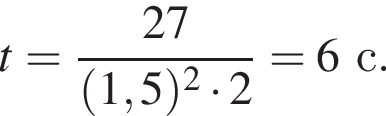
Ответ: 6.
13. Укажите решение системы неравенств:
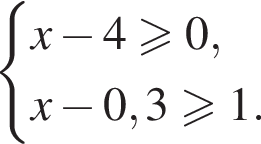
| 1) 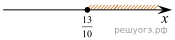
| 2) 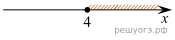
|
| 3) 
| 4) 
|
Решение. Решим систему:
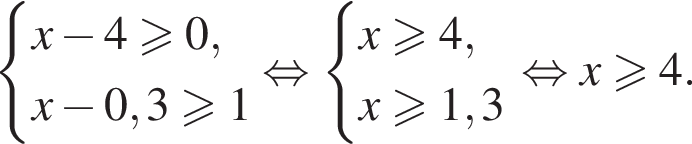
Данное решение соответствует варианту 2).
Ответ: 2.
14. Вере надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней.
Решение. В первый день Вера подписала  открыток, во второй —
открыток, во второй — 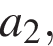 …, в последний —
…, в последний — 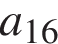 открыток. Всего было подписано
открыток. Всего было подписано  открыток. Если количество подписываемых открыток увеличивалось на d каждый день, то
открыток. Если количество подписываемых открыток увеличивалось на d каждый день, то
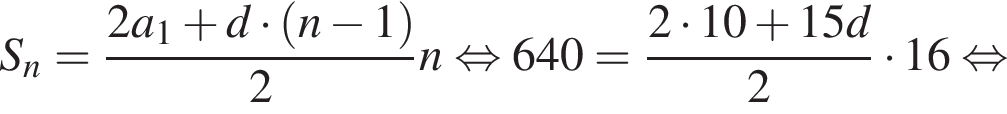
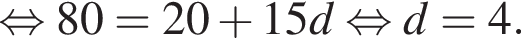
Тогда
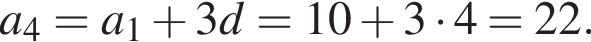
Следовательно, за четвертый день было подписано 22 открытки.
Ответ: 22.
15. 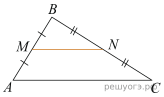 Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 31, сторона BC равна 42, сторона AC равна 50. Найдите MN
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 31, сторона BC равна 42, сторона AC равна 50. Найдите MN
Решение. Поскольку MN соединяет середины двух сторон треугольника ABC, MN является средней линией, она параллельна AC и равна её половине:
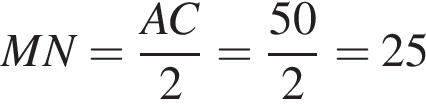
Ответ: 25
16. 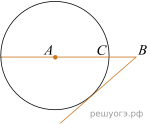 На отрезке AB выбрана точка C так, что
На отрезке AB выбрана точка C так, что 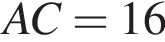 и
и  . Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Решение. 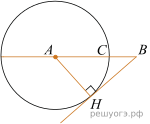 Проведём радиус AH в точку касания. Из прямоугольного треугольника ABH по теореме Пифагора найдём
Проведём радиус AH в точку касания. Из прямоугольного треугольника ABH по теореме Пифагора найдём 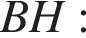
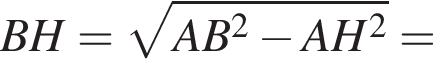
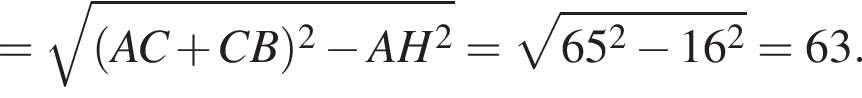
Ответ: 63.
17.  Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение. Пусть R и D соответственно радиус и диаметр окружности, a — сторона квадрата. Сторона квадрата равна диаметру вписанной окружности. Найдём площадь квадрата:
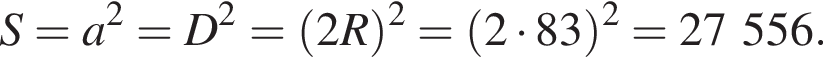
Ответ: 27 556.
18.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
Решение. Длина средней линии трапеции есть полусумма оснований, следовательно: 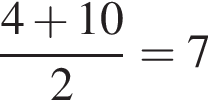
Ответ: 7.
19. Какие из следующих утверждений верны?
1) В треугольнике против меньшего угла лежит большая сторона.
2) Если один угол треугольника больше 120°, то два других его угла меньше 30°.
3) Если все стороны треугольника меньше 1, то и все его высоты меньше 1.
4) Сумма острых углов прямоугольного треугольника не превосходит 90°.
Решение. Проверим каждое из утверждений.
1) «В треугольнике против меньшего угла лежит большая сторона.» — неверно, в треугольнике напротив большего угла лежит большая сторона.
2) «Если один угол треугольника больше 120°, то два других его угла меньше 30°.» — неверно, сумма углов в треугольнике равна 180°.
3) «Если все стороны треугольника меньше 1, то и все его высоты меньше 1.» — верно, перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.
4) «Сумма острых углов прямоугольного треугольника не превосходит 90°.» — верно, сумма острых углов треугольника равна 90°.
Ответ: 34.
20. Сократите дробь
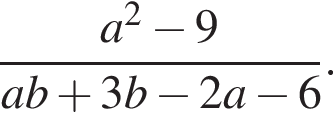
Решение. Имеем:
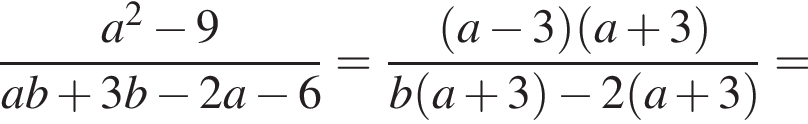
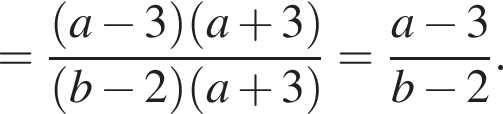
Ответ: 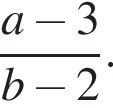
21. Свежие фрукты содержат 88 % воды, а высушенные — 30 %. Сколько требуется свежих фруктов для приготовления 6 кг высушенных фруктов?
Решение. Заметим, что сухая часть свежих фруктов составляет 12%, а высушенных — 70%. Значит, для приготовления 6 кг высушенных фруктов требуется 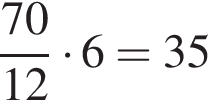 кг свежих.
кг свежих.
Ответ: 35 кг.
22. Постройте график функции
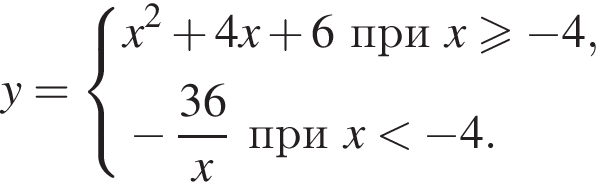
Определите, при каких значениях m прямая y = m имеет с графиком ровно одну общую точку.
Решение. 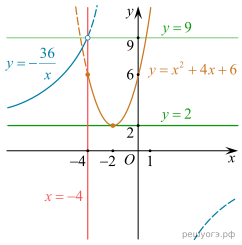 Преобразуем первое выражение:
Преобразуем первое выражение: 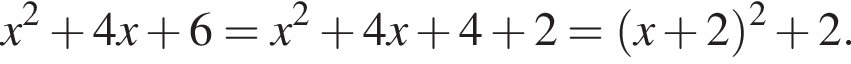 График функции
График функции 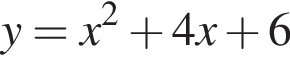 получается из графика функции
получается из графика функции  сдвигом на две единицы влево и две единицы вверх. Построим на
сдвигом на две единицы влево и две единицы вверх. Построим на 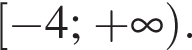
График функции 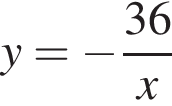 получается из графика функции
получается из графика функции 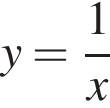 растяжением в 36 раз вдоль оси ординат и отражением относительно оси абсцисс. Построим на
растяжением в 36 раз вдоль оси ординат и отражением относительно оси абсцисс. Построим на 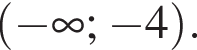
Из графика видно, что прямая y = m имеет одну точку пересечения с графиком при 0 y y ⩾ 9.
Ответ: 
23. Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 135°, а CD = 17.
Решение. 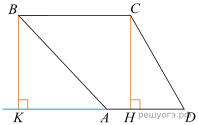 Введём обозначения, как показано на рисунке. Проведём высоты CH и
Введём обозначения, как показано на рисунке. Проведём высоты CH и 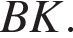 В трапеции сумма смежных углов при боковой стороне равна 180°, поэтому
В трапеции сумма смежных углов при боковой стороне равна 180°, поэтому 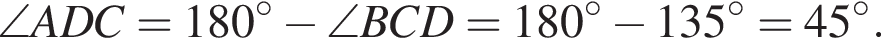 Из прямоугольного треугольника CHD найдём сторону
Из прямоугольного треугольника CHD найдём сторону 
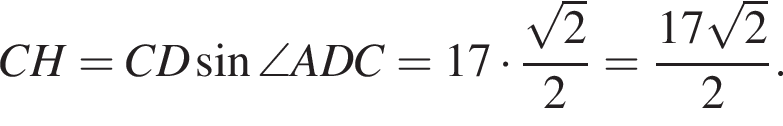
Углы ABC и BAK равны как накрест лежащие углы при параллельных прямых. Высоты CH и BK равны. Из прямоугольного треугольника ABK найдём 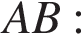
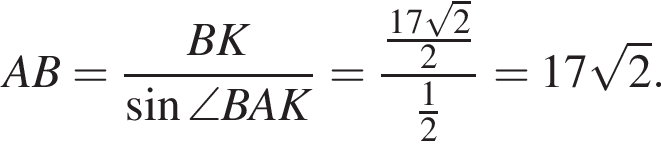
Ответ: 
24. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке E стороны BC. Докажите, что E — середина BC.
Решение. 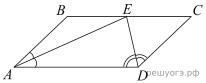 По определению параллелограмма
По определению параллелограмма 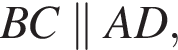 AE — секущая при параллельных прямых, следовательно, углы BEA и EAD равны как накрест лежащие. Поскольку
AE — секущая при параллельных прямых, следовательно, углы BEA и EAD равны как накрест лежащие. Поскольку  треугольник ABE — равнобедренный, откуда
треугольник ABE — равнобедренный, откуда 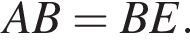 Аналогично, треугольник CED — равнобедренный и
Аналогично, треугольник CED — равнобедренный и 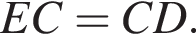 Стороны AB и CD равны, как противоположные стороны параллелограмма, следовательно:
Стороны AB и CD равны, как противоположные стороны параллелограмма, следовательно:
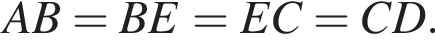 Таким образом, точка E — середина стороны
Таким образом, точка E — середина стороны 
25. Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Решение.  Введём обозначения, как показано на рисунке. Отрезок
Введём обозначения, как показано на рисунке. Отрезок 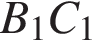 проходит через центр описанной окружности, следовательно,
проходит через центр описанной окружности, следовательно, 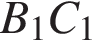 — диаметр. Углы
— диаметр. Углы 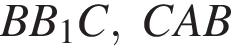 и
и 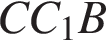 — вписанные и опираются на одну и ту же дугу, значит, они равны. Из прямоугольного треугольника
— вписанные и опираются на одну и ту же дугу, значит, они равны. Из прямоугольного треугольника 
 Из прямоугольного треугольника
Из прямоугольного треугольника 
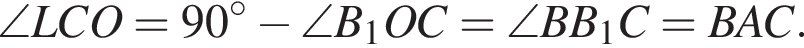 Рассмотрим прямоугольный треугольник CAM, углы BAC и
Рассмотрим прямоугольный треугольник CAM, углы BAC и  равны, значит,
равны, значит, 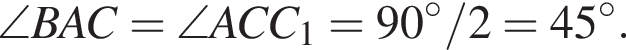
Ответ: 45°.
| № задания | ответ |
| 1 | 19,2 |
| 2 | 1000 |
| 3 | 5870 |
| 4 | 23 315 |
| 5 | 33,8 |
| 6 | -15 |
| 7 | 3 |
| 8 | 110 |
| 9 | -73 |
| 10 | 0,6 |
| 11 | 413 |
| 12 | 6 |
| 13 | 2 |
| 14 | 22 |
| 15 | 25 |
| 16 | 63 |
| 17 | 27 556 |
| 18 | 7 |
| 19 | 34 |
| 20 | 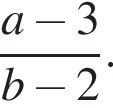
|
| 21 | 35 |
| 22 | 
|
| 23 | 
|
| 24 | - |
| 25 | 45 |









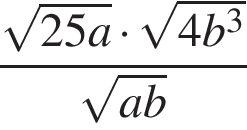 при a = 7 и b = 11.
при a = 7 и b = 11.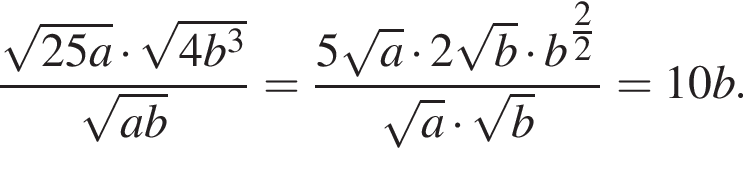
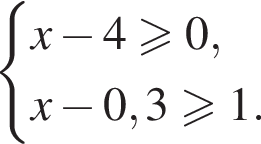
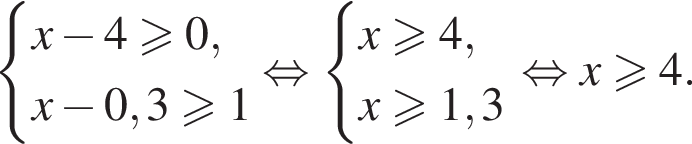
 Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 31, сторона BC равна 42, сторона AC равна 50. Найдите MN
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 31, сторона BC равна 42, сторона AC равна 50. Найдите MN На отрезке AB выбрана точка C так, что
На отрезке AB выбрана точка C так, что  Проведём радиус AH в точку касания. Из прямоугольного треугольника ABH по теореме Пифагора найдём
Проведём радиус AH в точку касания. Из прямоугольного треугольника ABH по теореме Пифагора найдём  Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
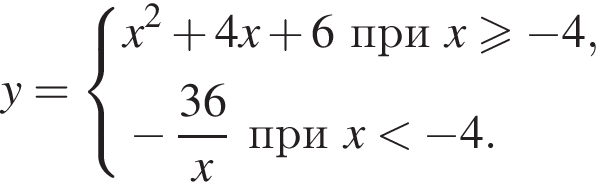
 Преобразуем первое выражение:
Преобразуем первое выражение:  Введём обозначения, как показано на рисунке. Проведём высоты CH и
Введём обозначения, как показано на рисунке. Проведём высоты CH и 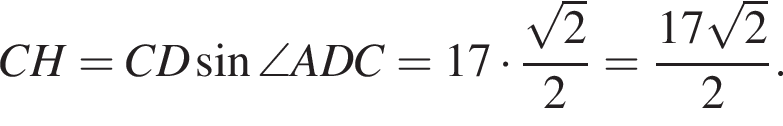
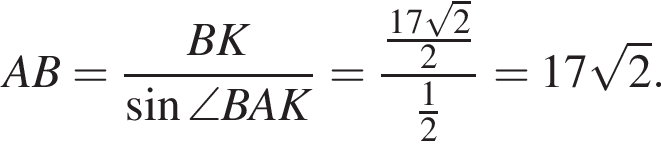
 По определению параллелограмма
По определению параллелограмма  Введём обозначения, как показано на рисунке. Отрезок
Введём обозначения, как показано на рисунке. Отрезок 









