8 класс Геометрия 12.11.20 Теория. Осевая и центральная симметрия. Ссылка на видео-урок https://youtu.be/hgbLUhEnvJY

12.11.2020г.

Геометрия

8 а/б класс. Ссылка на видеоурок https://youtu.be/hgbLUhEnvJY

Тема урока: Осевая и центральная симметрия геометрических фигур

В учебнике- эта тему можешь прочитать на странице 110, п. 47.

Открой тетрадь и запиши число на полях и «Классная работа».

Ниже запиши тему урока.

Сегодня мы поговорим о понятиях осевая и центральная симметрия геометрических фигур.

Самые важные моменты теории этой темы запиши в тетрадь.

Осевая симметрия

Слово «симметрия»- это греческое слово, которое означает соразмерность, пропорциональность, одинаковость в расположении частей.

Две точки А и В называются симметричными относительной прямой а, если эта прямая проходит через середину отрезка АВ и перпендикулярна к нему.

К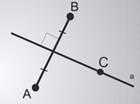 аждая точка прямой а считается симметричной самой себе. 

На рисунке точки А и В симметричны относительно прямой а, а точка С, принадлежащая прямой а, симметрична самой себе относительно этой прямой.

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.

Прямая а называется осью симметрии фигуры. А про фигуру говорят, что она обладает осевой симметрией.

В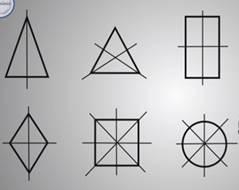 геометрии много фигур, обладающих осевой симметрией. 

Например: неразвернутый угол имеет одну ось симметрии – это прямая, на которой расположена биссектриса этого угла; 

равнобедренный треугольник имеет тоже одну ось симметрии, а равносторонний – три; 

квадрат – четыре оси; 

окружность – бесконечное множество осей симметрии. 

А вот параллелограмм, отличный от прямоугольника и ромба, не имеет ни одной оси симметрии.

Как же построить точку В, симметричную точке А относительно прямой в? 

Для этого через точку А нужно провести перпендикуляр к прямой в и отложить на нем отрезок ОВ, равный отрезку ОА, где О - точка пересечения перпендикуляра с прямой в.

Центральная симметрия

Две точки А и В называются симметричными относительно точки О, если О – середина отрезка АВ.

Т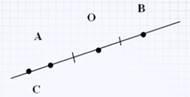 очка О считается симметричной самой себе. 

На рисунке точки А и В симметричны относительно точки О, а точки С и В не симметричны относительно этой точки.

Для построения точки В, симметричной точке А относительно точки О, нужно провести прямую через точки А и О и на продолжении от точки О отложить отрезок ОВ, равный ОА.

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.

Точка О называетсяцентром симметрии фигуры. А про фигуру говорят, что она обладает центральной симметрией.

Центральной симметрией обладают окружность, параллелограмм, квадрат.

А вот произвольный т реугольник не имеет центра симметрии.

Если оглянуться вокруг, то можно встретить фигуры, изображения которых симметричны.

Симметрия присуща всем формам в природе и является одним из основополагающих принципов красоты.

Если взглянуть на любое живое существо, сразу бросается в глаза симметричность устройства организма.

Нагляднее всего симметрия видна в архитектуре: Пирамида Хеопса в Египте, Собор Парижской Богоматери, Эйфелева башня во Франции.

Теперь рассмотрим алгоритм построения симметричной точки относительно прямой. Запиши его в терадь и зарисуй.
Дана точка А и прямая а. Необходимо построить симметричную ей точку точку А₁ относительно прямой а.

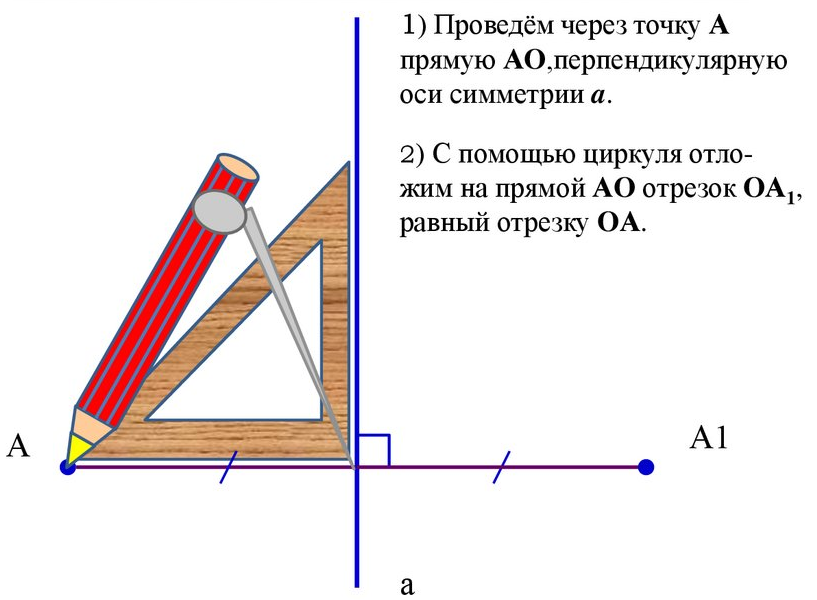
Чтобы построить симметричный отрезок относительно прямой необходимо построить симметричные точки для начала и конца данного отрезка, например, для А – А₁, для В – В_1. Затем соединить новые точки, таким образом получится новый отрезок А₁В₁ – симметричный данному отрезку АВ.

Для фигуры необходимо построить все симметричные точки для вершин этой фигуры, затем соединить новые точки между собой и обозначить их.

Таким образом, вы научились строить симметричные точки, отрезки, геометрические фигуры относительно оси симметрии.

Теперь необходимо выполнить самостоятельную работу из Урока 2 по этой теме и прислать учителю для проверки.