Вариант № 9
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на рисунке. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Город Гранюк | Деревня Астрелка | Хутор Южный | Город Гусевск |
| Цифры |
|
|
|
|
Андрей и его друзья собираются поехать в отпуск на две недели. Предварительно они наметили маршрут, представленный на рисунке. Они планируют на велосипедах добраться от города Гранюк до кемпинга, обозначенного на рисунке цифрой 7, за 4 дня, а потом поставить там палатки и отдыхать в море. Друзья собираются выехать рано утром и в первый день добраться до хутора Южный, где живёт бабушка Андрея. Там есть озеро, в котором можно купаться и ловить рыбу, что они и собираются делать до обеда следующего дня. Потом планируется доехать до посёлка Быково и заночевать там в мини‐отеле. На следующий день они собираются проехать 24 км до города Гусевск вдоль степного заказника и переночевать в одной из гостиниц. Заказник обозначен на рисунке цифрой 8. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Прямой путь короче, но там в эти дни идёт ремонт дороги, и пока неизвестно, где можно будет проехать быстрее.
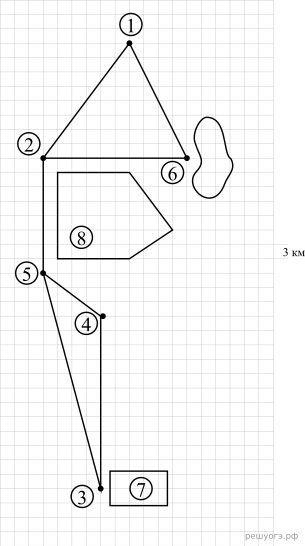
Решение. Андрей и его друзья собираются начинать движение из города Гранюк, следовательно, он отмечен на рисунке цифрой 1. Рядом с хутором Южный расположено озеро. Значит, хутор Южный отмечен на рисунке цифрой 6. После хутора Южный планируется поехать до посёлка Быково, а потом проехать до города Гусевска вдоль степного заказника. Значит, город Гусевск обозначен на рисунке цифрой 5. Из Гусевска в посёлок Домарку, где расположен кемпинг, можно доехать напрямую или через деревню Астрелка. Значит, деревня Астрелка обозначена на рисунке цифрой 4.
Ответ: 1465.
2. Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели? В каждой пачке 25 пакетиков чая.
Решение. Найдём, сколько пакетиков чая ребята потратят за две недели:
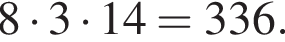
Значит, им понадобится
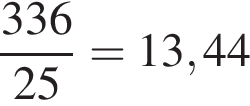 пачек чая.
пачек чая.
Таким образом, ребята должны купить 14 пачек чая.
Ответ: 14.
3. Найдите площадь (в км2), которую занимает заказник.
Решение.  Площадь заказника равна:
Площадь заказника равна:
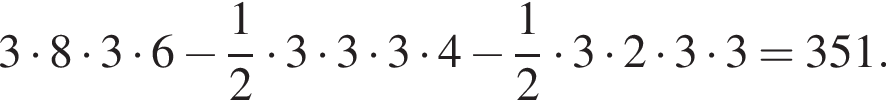
Ответ: 351.
4. Все могут пойти в отпуск с 15 июля, кроме Григория и Марии, которым в этот день нужно работать. Они готовы выехать 16 июля и догнать остальную группу в посёлке Быково, не заезжая на хутор Южный. Найдите расстояние, которое проедут Григорий и Мария от города Гранюк до Быково. Ответ дайте в километрах.
Решение. Найдём расстояние, которое проедут Григорий и Мария от города Гранюк до Быково, по теореме Пифагора:
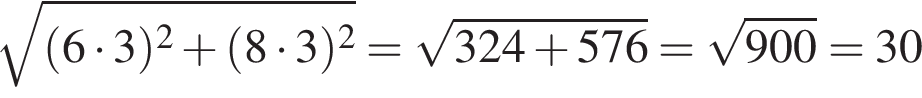 км.
км.
Ответ: 30.
5. Андрей выяснил, что его велосипед пришёл в нерабочее состояние. Андрей посетил сайты интернет‐магазина «ОК» и магазина «Вело», расположенного в соседнем доме, чтобы узнать некоторые цены. В этих магазинах можно купить готовый велосипед либо запасные части. Цены на продукцию магазинов и срок доставки из интернет‐магазина даны в таблице.
| Продукция | Цена в магазине
«Вело» (руб.) | Цена в магазине
«ОК» (руб.) | Срок доставки из
магазина «ОК» (дни) |
| Подсветка для спиц | 190 | 180 | 3 |
| Шина вида «А» | 680 | 650 | 12 |
| Шина вида «Б» | 1680 | 1450 | 12 |
| Спица | 70 | 80 | 3 |
| Педаль вида «А» | 437 | 405 | 10 |
| Педаль вида «Б» | 860 | 750 | 10 |
| Тормоз вида «А» | 1130 | нет | 10 |
| Тормоз вида «Б» | нет | 2180 | 10 |
| Набор крепёжных изделий | 740 | 765 | 14 |
Андрея не устраивает срок доставки деталей из интернет‐магазина, и он решил приобрести детали в магазине «Вело». Он готов потратить на ремонт не более 6000 рублей и при этом хочет купить самый дорогой набор для ремонта велосипеда, который может себе позволить. Ему нужно купить 5 спиц, 2 шины (одного вида), 2 педали (одного вида), тормоз (любого вида) и набор крепёжных изделий. Сколько рублей Андрей потратит на набор запасных частей?
Решение. На спицы Андрей потратит 70 · 5 = 350 руб. Далее, Андрей должен купить две шины вида «А», поскольку если он купит две шины вида «Б», ему не хватит денег на остальные запчасти. Значит, на шины он потратит 680 · 2 = 1360 руб. Поскольку Андрей хочет купить самый дорогой набор для ремонта велосипеда, из двух видов педалей он может купить педали вида «Б», они будут стоить 860 · 2 = 1720 руб. Ему останется купить тормоз и набор крепёжных изделий. Таким образом, всего Андрей потратит:
 руб.
руб.
Ответ: 5300.
Приведем другое решение.
Спицы, тормоз и набор крепежных изделий в магазине имеются только одного вида. На них Андрей потратит
 руб.
руб.
Следовательно, у него останется 6000 − 2220 = 3780 руб.
Если Андрей купит шины вида «Б», то он потратит на них 2 · 1680 = 3360 руб. и у него не останется денег на педали. Следовательно, Андрей должен купить шины вида «А». На них он потратит 2 · 680 = 1360 руб. и для покупки педалей останется еще 3780 − 1360 = 2420 руб. Следовательно, Андрей может купить педали вида «Б». На них он потратит 2 · 860 = 1720 руб. Общая сумма покупок составит
 руб.
руб.
6. Найдите значение выражения 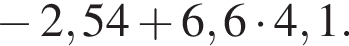
Решение. Выполним умножение, затем сложение:
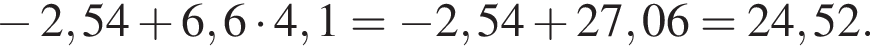
Ответ: 24,52.
7. На координатной прямой отмечены числа a, b, и c.
В ответе укажите номер правильного варианта.

Укажите номер верного утверждения.
1) 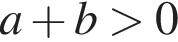
2) 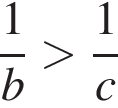
3) 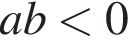
4) 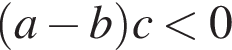
Решение. Заметим, что 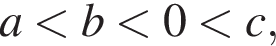 откуда
откуда 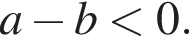 Рассмотрим каждое утверждение:
Рассмотрим каждое утверждение:
1) 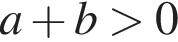 — неверно.
— неверно.
2) 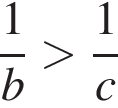 — неверно.
— неверно.
3) 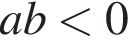 — неверно.
— неверно.
4) 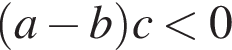 — верно.
— верно.
Правильный ответ указан под номером: 4.
8. Найдите значение выражения 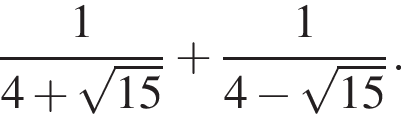
Решение. Вычислим:
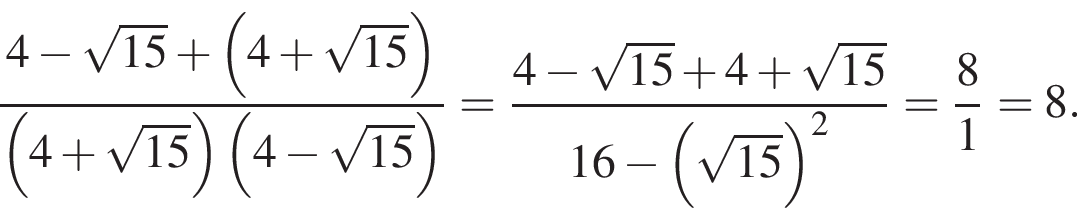
Ответ: 8.
9. Решите уравнение 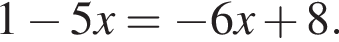
Решение. Последовательно получаем:
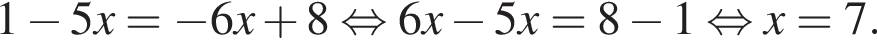
Ответ: 7.
10. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Решение. Всего спортсменов 11 + 6 + 3 = 20 человек. Поэтому вероятность того, что первым будет стартовать спортсмен не из России равна 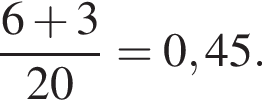
Ответ: 0,45.
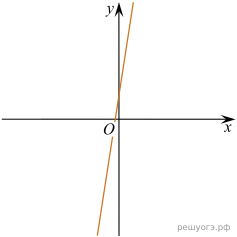
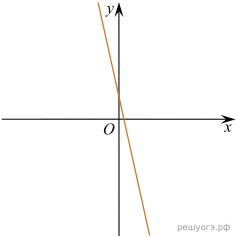
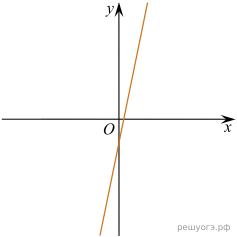
11. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
Графики
Коэффициенты
| 1) k b 0 | 2) k 0, b 0 | 3) k b | 4) k 0, b |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Решение. Если прямая задана уравнением 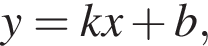 то при
то при  функция возрастает, при
функция возрастает, при  — убывает. Значению b соответсвует значение функции в точке
— убывает. Значению b соответсвует значение функции в точке  Таким образом, графику A соответствуют коэфициенты 2, Б − 1, В − 4.
Таким образом, графику A соответствуют коэфициенты 2, Б − 1, В − 4.
Ответ: 214.
12. Площадь любого выпуклого четырехугольника можно вычислять по формуле 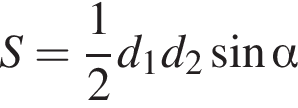 , где
, где 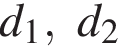 — длины его диагоналей, а
— длины его диагоналей, а 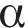 угол между ними. Вычислите
угол между ними. Вычислите  , если
, если  .
.
Решение. Выразим  :
:
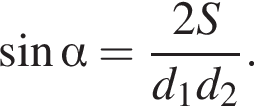
Подставляя, получаем:
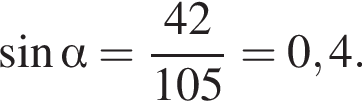
Ответ: 0,4.
13. На каком рисунке изображено множество решений неравенства 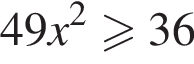 ?
?
| 1) 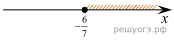
| 2) 
|
| 3) 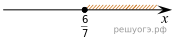
| 4) 
|
Решение. Решим неравенство:
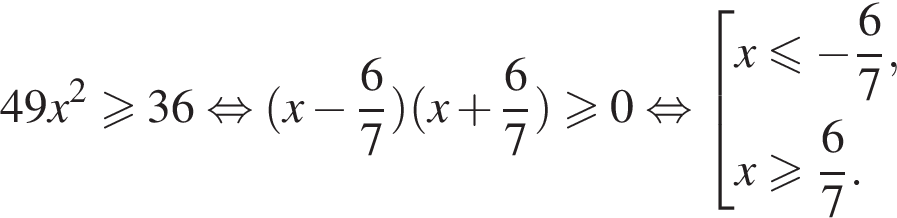
Ответ: 4.
14. Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.
Решение. В первый день турист прошел  км, во второй —
км, во второй — 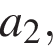 …, в последний —
…, в последний —  км. Всего он прошел
км. Всего он прошел 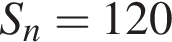 км. Если каждый день турист проходил больше, чем в предыдущий день, на d км, то
км. Если каждый день турист проходил больше, чем в предыдущий день, на d км, то
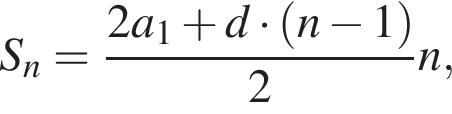
где  дней,
дней,  км. Таким образом,
км. Таким образом,
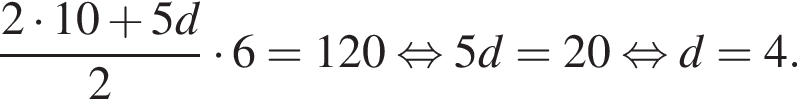
Тогда за третий день турист прошел
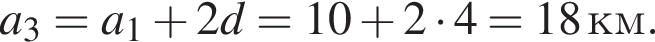
Ответ: 18.
15.  Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.
Решение. Углы А и В — односторонние, поэтому угол В равен 180° − 45° − 30° = 105°.
Ответ: 105.
16.
Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
Решение. Дуга FD, не содержащая точку Е, равна 360° − 150° − 68° = 142°, поэтому ∠DEF = 71°.
Ответ: 71.
17.  Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Решение. Площадь параллелограмма равна произведению высоты на основание, поэтому она равна 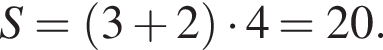
Ответ: 20.
18.  На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
Решение. Посчитаем количество клеток внутри закрашенной области: их 9.
Ответ: 9.
19. Какие из следующих утверждений верны?
1) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
2) Боковые стороны любой трапеции равны.
3) Один из углов треугольника всегда не превышает 60 градусов.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение. Рассмотрим каждое из утверждений:
1) «Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне» — верно, так как ромб — это частный случай параллелограмма и его площадь есть произведение его стороны на высоту, проведённую к этой стороне.
2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.
3) «Один из углов треугольника всегда не превышает 60 градусов» — верно, наименьший угол в любом треугольнике всегда не превышает 60 градусов.
Ответ: 13
20. Решите неравенство 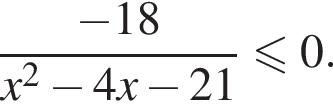
Решение. Решим неравенство методом интервалов, для этого, сначала разложим на множители выражение 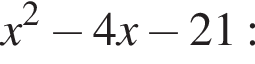

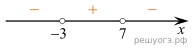
Теперь расставим точки на прямой и определим знаки выражения на каждом получившемся промежутке (см. рис.).
Таким образом, ответ 
Ответ: 
Примечание.
Обратите внимание, что при определении знаков выражения используется исходное выражение, а именно, 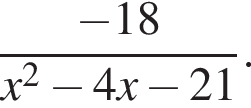
21. Имеются два сосуда, содержащие 40 кг и 30 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 73% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 72% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Решение. Пусть концентрация первого раствора - х, концентрация второго раствора - y. Составим систему уравнений согласно условию задачи:
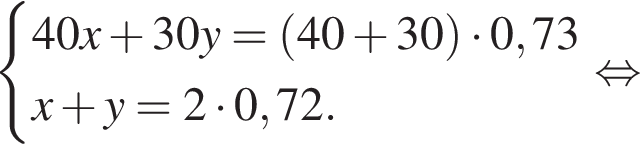
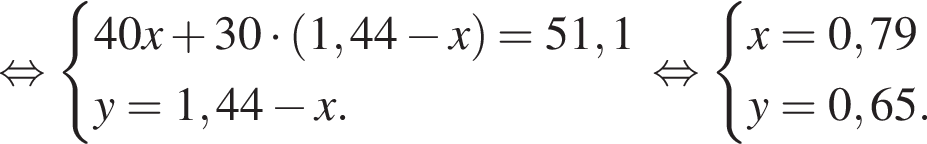
Таким образом, во втором растворе содержится 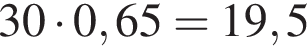 килограмма кислоты
килограмма кислоты
Ответ: 19,5
22. Известно, что графики функций 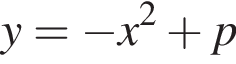 и
и  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Решение. Найдём абсциссы точек пересечения:
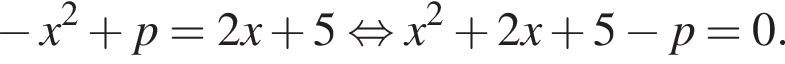
Графики функций, будут иметь ровно одну точку пересечения, если это уравнение имеет ровно одно решение. То есть, если дискриминант этого квадратного уравнения будет равен нулю.

Подставив параметр p в уравнение, найдём x координату точки пересечения этих функций:
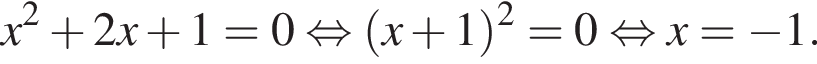
Координата y находится путём подстановки координаты x в любое из уравнений, например, во второе:
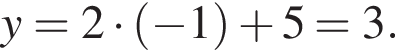
Теперь, зная p, можем построить графики обеих функций (см. рис.).
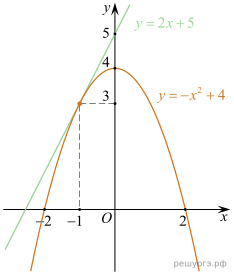
Ответ: (−1; 3).
23.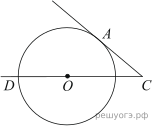
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140° .
Решение. 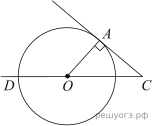 Проведём радиус AO в точку касания. Так как AO — радиус, а AC — касательная, то
Проведём радиус AO в точку касания. Так как AO — радиус, а AC — касательная, то  Угол AOD — центральный, следовательно, он равен величине дуги, на которую опирается,
Угол AOD — центральный, следовательно, он равен величине дуги, на которую опирается,  Угол DOC — развёрнутый, следовательно,
Угол DOC — развёрнутый, следовательно, 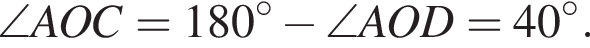
Из треугольника AOC, 
Ответ: 50°.
24. В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL = BM. Докажите, что данный параллелограмм — прямоугольник.
Решение.  Противоположные стороны параллелограмма равны, то есть
Противоположные стороны параллелограмма равны, то есть 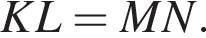 Рассмотрим треугольники KLB и BMN, в них KB равно BN, LB равно BM и KL равно MN, следовательно, треугольники равны по трём сторонам, а значит,
Рассмотрим треугольники KLB и BMN, в них KB равно BN, LB равно BM и KL равно MN, следовательно, треугольники равны по трём сторонам, а значит, 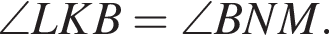
Вспомним также, что противоположные углы параллелограмма равны, следовательно:
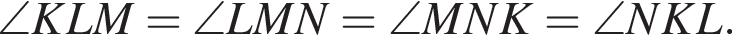
Сумма углов параллелограмма 360°:
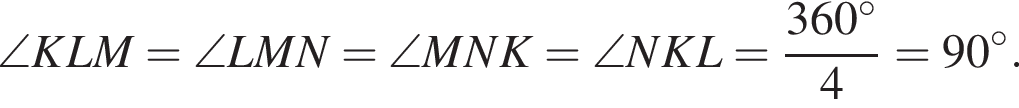
Все углы параллелограмм прямые, а следовательно, этот параллелограмм — прямоугольник.
25. В треугольнике ABC угол 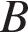 равен 120°, а длина стороны AB на
равен 120°, а длина стороны AB на 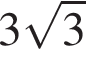 меньше полупериметра треугольника. Найдите радиус окружности, касающейся стороны BC и продолжений сторон AB и AC.
меньше полупериметра треугольника. Найдите радиус окружности, касающейся стороны BC и продолжений сторон AB и AC.
Решение. Центр окружности является точкой пересечения биссектрис углов CBM и BCL. При этом по свойству касательных  . Следовательно, длины ломаных ACK и ABK равны полупериметру p. По условию
. Следовательно, длины ломаных ACK и ABK равны полупериметру p. По условию 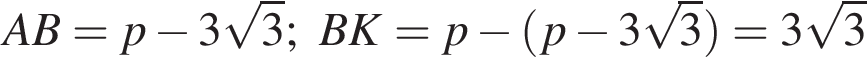 .
.
Найдем радиус KO из прямоугольного треугольника BKO. В треугольнике BKO

катет KO лежит против угла 30°, значит, 
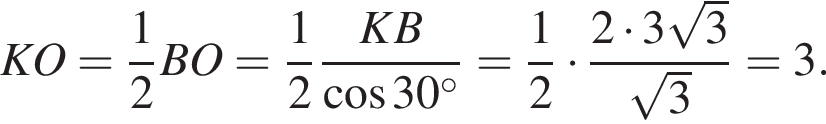
Ответ: 3.
| № задания | ответ |
| 1 | 1465 |
| 2 | 14 |
| 3 | 351 |
| 4 | 30 |
| 5 | 5300 |
| 6 | 24,52 |
| 7 | 4 |
| 8 | 8 |
| 9 | 7 |
| 10 | 0,45 |
| 11 | 214 |
| 12 | 0,4 |
| 13 | 4 |
| 14 | 18 |
| 15 | 105 |
| 16 | 71 |
| 17 | 20 |
| 18 | 9 |
| 19 | 13 |
| 20 | 
|
| 21 | 19,5 |
| 22 | (−1; 3). |
| 23 | 50 |
| 24 | - |
| 25 | 3 |







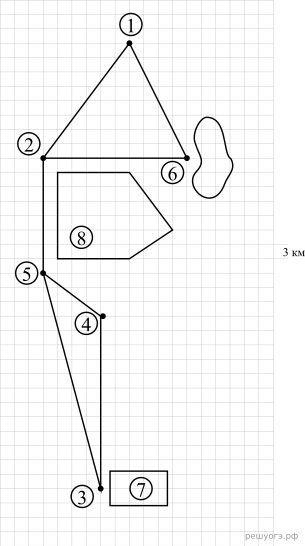
 Площадь заказника равна:
Площадь заказника равна: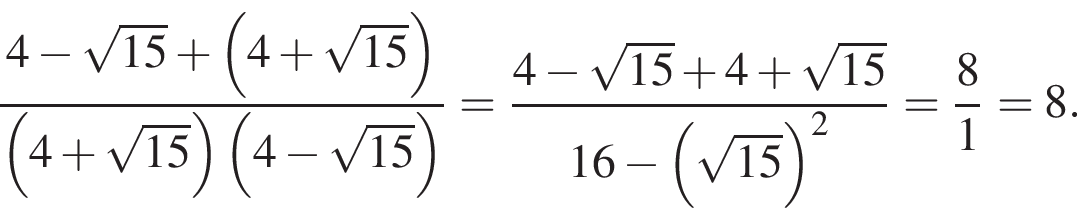
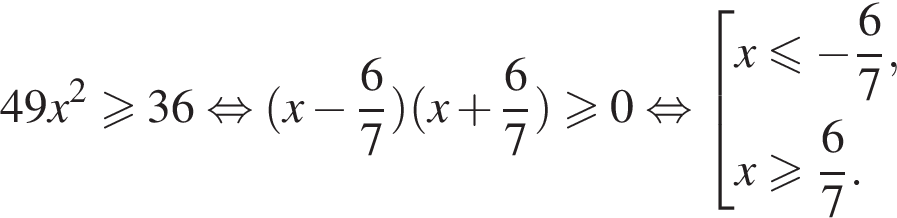
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.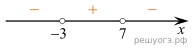
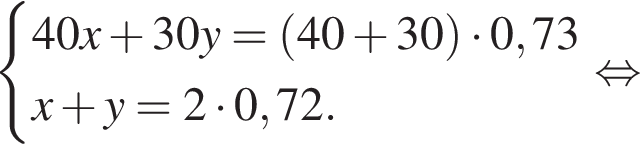
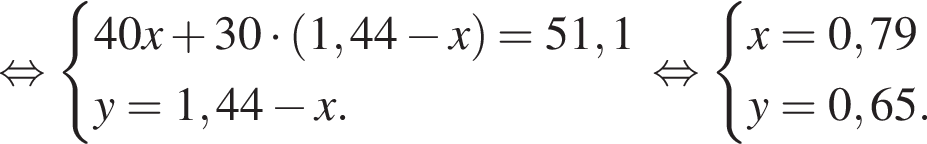
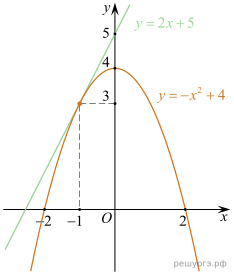

 Проведём радиус AO в точку касания. Так как AO — радиус, а AC — касательная, то
Проведём радиус AO в точку касания. Так как AO — радиус, а AC — касательная, то  Противоположные стороны параллелограмма равны, то есть
Противоположные стороны параллелограмма равны, то есть 










