Аксиомы стереометрии

Тема учебного занятия:

Взаимное расположение точек, прямых и плоскостей:

аксиомы стереометрии.

«Математику

уже затем учить надо,

что она ум

в порядок приводит»

Михаил Васильевич Ломоносов

Сегодня на занятии:

• проверим домашнее задание путем написания математического диктанта, фронтального опроса, индивидуальной работы по карточкам;
• заслушаем сообщения учащихся об аксиоматическом методе в геометрии;
• узнаем, как вы справились с дополнительным домашним заданием по подготовке математических сказок и стихов, а также узнаем ответы на вопросы исторической викторины;
• научимся работать с готовыми рисунками;
• научимся применять аксиомы стереометрии и следствия из них при решении задач.

Математический диктант

Математический диктант :

• раздел геометрии, который изучает свойства фигур на плоскости …
• раздел геометрии, который изучает свойства фигур в пространстве …
• геометрическое тело, поверхность которого состоит из конечного числа плоских многоугольников, любые два смежные из которых не лежат в одной плоскости …
• многогранник, имеющий шесть граней, которые являются равными квадратами …
• многогранник, у которого шесть граней и каждая из них - параллелограмм…
• параллелепипед, у которого боковые грани прямоугольники …
• параллелепипед, у которого все грани прямоугольники…
• многогранник, у которого две грани равные многоугольники, а остальные грани - параллелограммы…
• призма, у которой боковые грани - прямоугольники …
• призма, у которой боковые грани - прямоугольники, а ее основания – правильные многоугольники…
• многогранник, у которого одна грань - многоугольник, а остальные грани треугольники с общей вершиной…
• пирамида, у которой основание – правильный многоугольник, а все боковые ребра равны между собой …
• треугольная пирамида, у которой все грани – равные правильные треугольники…

Ответы:

• Планиметрия
• Стереометрия
• Многогранник
• Куб
• Параллелепипед
• Прямой параллелепипед
• Прямоугольный параллелепипед
• Призма
• Прямая призма
• Правильная призма
• Пирамида
• Правильная пирамида
• Тетраэдр

Фронтальный опрос

• Какие разделы геометрии вы знаете?

2. Дайте определение понятию «планиметрия».

3. Дайте определение понятию «стереометрия».

4. Назовите основные фигуры на плоскости.

5. Назовите основные фигуры в пространстве.

Фронтальный опрос

• Что дает нам наглядное представление об основных фигурах в пространстве?

• Какие геометрические тела вы знаете?

• С какими геометрическими телами мы познакомились.

• Какое геометрическое тело называется многогранником?

• Назовите виды многогранников, которые вы знаете.

Фронтальный опрос

• Какой многогранник называется кубом?

• Какой многогранник называется параллелепипедом?

• Какой параллелепипед называется прямым?

• Какой параллелепипед называется прямоугольным?

• Какой многогранник называется призмой?

Фронтальный опрос

• Какая призма называется прямой?

• Какая призма называется правильной?

• Какой многогранник называется пирамидой?

• Какая призма называется правильной?

• Какая пирамида называется тетраэдром?

Историческая справка «Аксиомы. Аксиоматический метод»

Геометрия является иллюстрацией метода построения теории, которая получила название аксиоматического метода.

Система Евклида явилась первым опытом применения аксиоматического метода и просуществовала без изменений до XIX века н. э. Однако она обладала рядом недостатков с современной точки зрения на аксиоматический метод, и на рубеже XIX–XX веков была построена геометрическая система, свободная от этих недостатков.

Суть аксиоматического метода построения научной теории состоит в следующем:

• перечисляются основные (неопределяемые) понятия,
• все вновь возникающие понятия должны быть определены через основные понятия и понятия, определенные ранее.

Фронтальный опрос

21. Какое утверждение называется аксиомой?

АКСИОМА - исходное положение научной теории, принимаемое без доказательства

22. Сколько аксиом стереометрии мы знаем?

23. Сформулируйте аксиомы стереометрии?

А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна

А2. Если две точки прямой лежат в плоскости, то и все точки прямой лежат в этой плоскости

А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

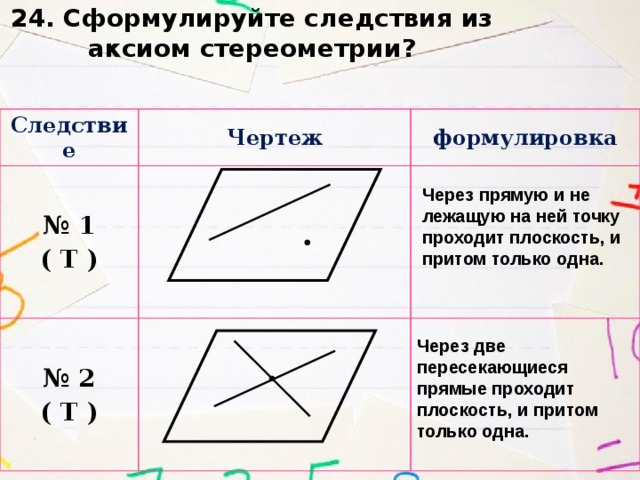
24. Сформулируйте следствия из аксиом стереометрии?

Следствие

Чертеж

№ 1

( Т )

№ 2

формулировка

( Т )

Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Через две пересекающиеся прямые проходит плоскость, и притом только одна.

25. Что описывают аксиомы стереометрии?

А2.

А1.

А3.

Взаимное расположение прямой и плоскости

Взаимное расположение плоскостей

Способ задания плоскости .

А

b

В

А

b

В

С

b

a

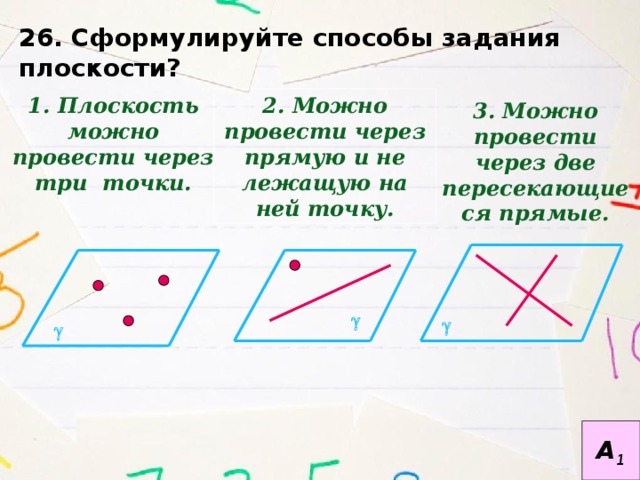
26. Сформулируйте способы задания плоскости?

2. Можно провести через прямую и не лежащую на ней точку.

1. Плоскость можно провести через три точки.

3. Можно провести через две пересекающиеся прямые.

g

g

g

А 1

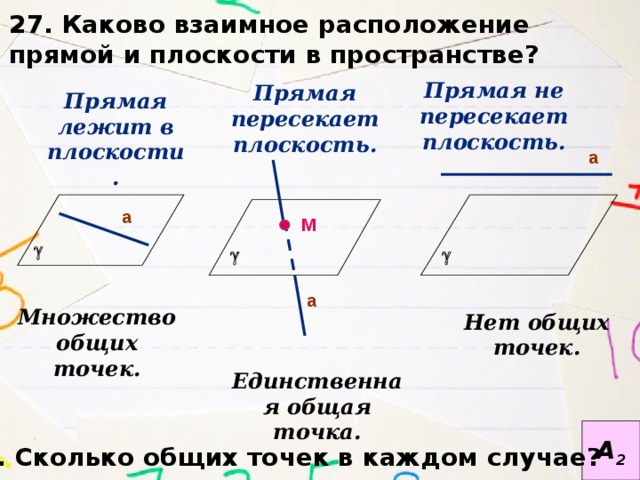
27. Каково взаимное расположение прямой и плоскости в пространстве?

Прямая не пересекает плоскость.

Прямая пересекает плоскость.

Прямая лежит в плоскости.

а

а

М

g

g

g

а

Множество общих точек.

Нет общих точек.

Единственная общая точка.

А 2

28. Сколько общих точек в каждом случае?

Определите, о каких аксиомах или следствиях из аксиом идет речь

На трех морях живут киты,

На синих трех морях.

На трех китах стоит Земля,

На трех больших китах.

Три точки – это якоря

Для плоскости одной.

И хоть в китов не верю я,

Но пусть по плоскости меня

Сейчас троллейбус номер «три»

Быстрей умчит.

Определите, о каких аксиомах или следствиях из аксиом идет речь

Говорит прямой прямая:

- Я единственная знаю,

Как в далекий путь с тобой,

Даже в плоскости одной,

Мне отправиться, сестрица…

Точка А тут пригодится.

Не знакома с нею ты,

Ну, да это полбеды;

Раз нам, видно, все равно

Пересечься не дано,

Пусть она хоть в том поможет,

Что единый курс проложит!

Самостоятельная работа

Ф.И. учащегося ____________________________________________________

Запишите:

• Название многогранника __________________________________
• Количество вершин _________________
• Перечислите вершины __________________________________
• Количество ребер ___________________
• Перечислите ребра _________________

__________________________________

• Количество граней _________________

• Перечислите грани _________________

__________________________________

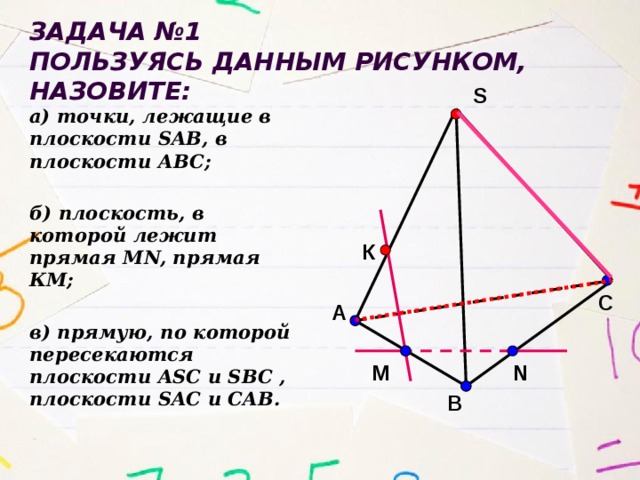
Задача №1

Пользуясь данным рисунком, назовите:

S

а) точки, лежащие в плоскости SAB, в плоскости АВС;

б) плоскость, в которой лежит прямая MN, прямая КМ;

в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB.

К

C

А

N

М

В

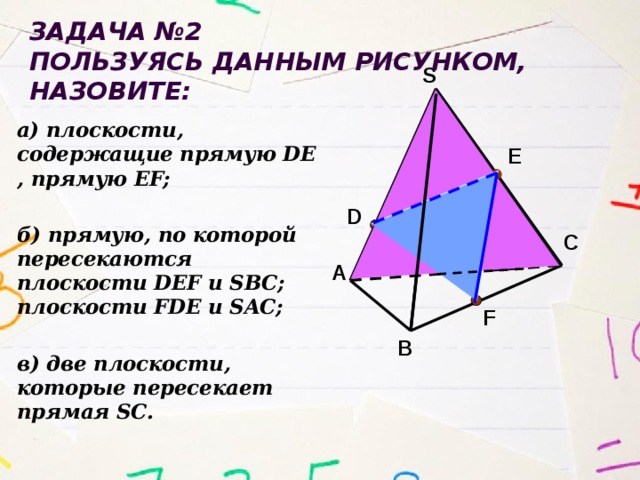
Задача №2

Пользуясь данным рисунком, назовите:

S

а) плоскости, содержащие прямую DE , прямую EF;

б) прямую, по которой пересекаются плоскости DEF и SBC; плоскости FDE и SAC;

в) две плоскости, которые пересекает прямая SС.

E

D

С

А

F

В

Задача №3

Пользуясь данным рисунком, назовите:

B 1

C 1

плоскости, содержащие прямую В 1 С

A 1

D 1

B

C

A

D

В 1

C 1

А 1

D 1

В 1 С

?

В

С

А

D

В 1

C 1

А 1

D 1

В 1 С

?

В

С

А

D

Задача №4. Пользуясь данным рисунком, назовите:

D 1

С 1

А 1

В 1

α

D

С

А

В

• несколько точек, которые лежат в

плоскости α.

D 1

С 1

А 1

В 1

α

D

С

А

В

2) несколько точек, которые не лежат в

плоскости α.

D 1

С 1

А 1

В 1

α

D

С

А

В

3) несколько прямых, которые лежат в

плоскости α.

D 1

С 1

А 1

В 1

α

D

С

А

В

4) несколько прямых, которые не лежат в

плоскости α.

D 1

С 1

А 1

В 1

α

D

С

А

В

5) несколько прямых, которые пересекают

прямую ВС

D 1

С 1

А 1

В 1

α

D

С

А

В

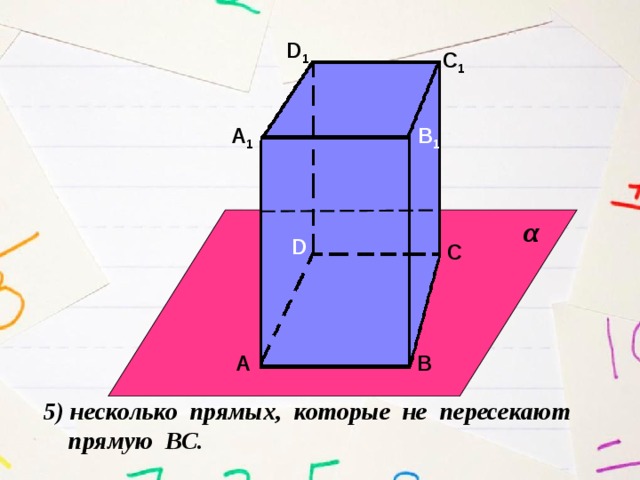
5) несколько прямых, которые не пересекают

прямую ВС.

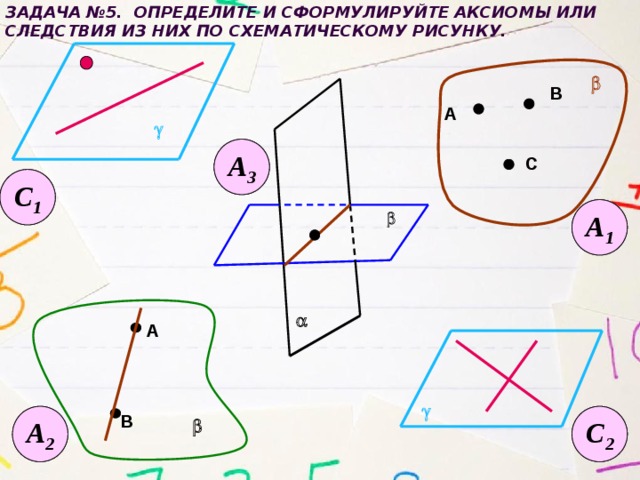
Задача №5. Определите и сформулируйте аксиомы или следствия из них по схематическому рисунку.

b

В

А

g

А 3

2

С

С 1

1

А 1

3

b

a

А

g

В

4

5

А 2

С 2

b

Решение задач

Взаимное расположение точек, прямых и плоскостей:

аксиомы стереометрии.

Задача №1.

Точка М лежит на

ребре DD 1

Дан куб АВСDA 1 B 1 C 1 D 1.

D 1

Точка N лежит на

С 1

ребре CC 1

M

В 1

А 1

Точка K лежит на

ребре BB 1

N

D

С

K

А

В

• Назовите плоскости в которых лежат

точка М, точка N.

M: ADD 1 и D 1 DC; N: CC 1 D 1 и BB 1 C 1

Дан куб АВСDA 1 B 1 C 1 D 1.

Точка М лежит на

ребре DD 1

D 1

С 1

Точка N лежит на

ребре CC 1

M

В 1

А 1

Точка K лежит на

ребре BB 1

N

F

D

С

K

А

В

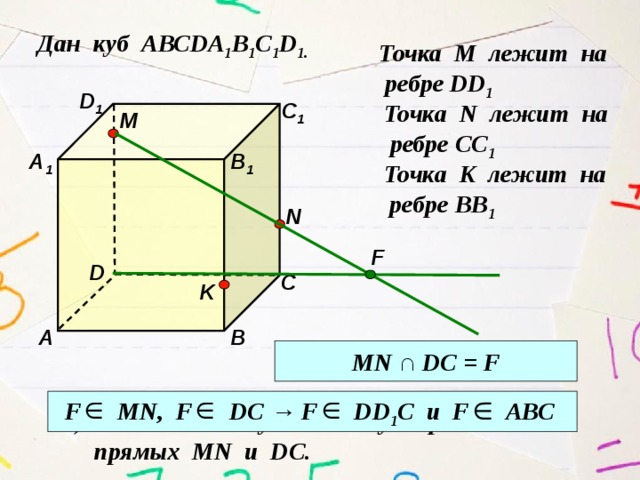
MN ∩ DC = F

Каким свойством обладает точка F?

F MN, F DC → F DD 1 C и F АВС

2) Найдите точку F – точку пересечения

прямых MN и DС.

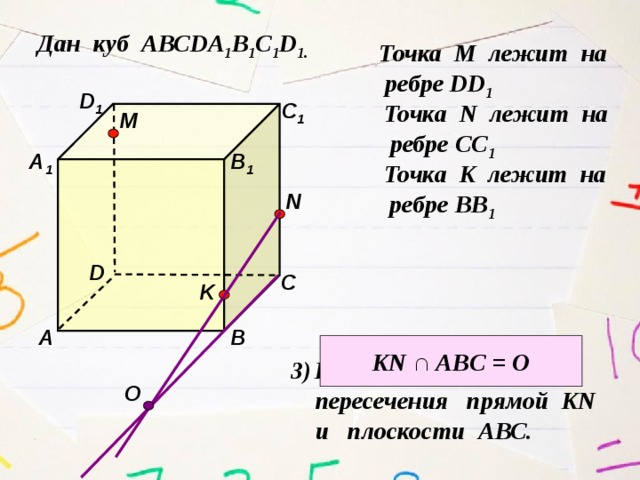
Дан куб АВСDA 1 B 1 C 1 D 1.

Точка М лежит на

ребре DD 1

D 1

Точка N лежит на

С 1

ребре CC 1

M

А 1

В 1

Точка K лежит на

ребре BB 1

N

D

С

K

В

А

KN ∩ ABC = O

• Найдите точку

пересечения прямой KN

и плоскости АВС.

О

Дан куб АВСDA 1 B 1 C 1 D 1.

Точка М лежит на

ребре DD 1

O  KN, значит О  МNK

O  OC, значит О  АВС

F  MN, значит F  MNK

F  DC, значит F  АВС

D 1

Точка N лежит на

С 1

ребре CC 1

M

А 1

В 1

Точка K лежит на

ребре BB 1

N

ABC ∩ MNK = OF

F

D

С

K

А

В

O

4) Найдите линию пересечения

плоскостей MNK и ABC.

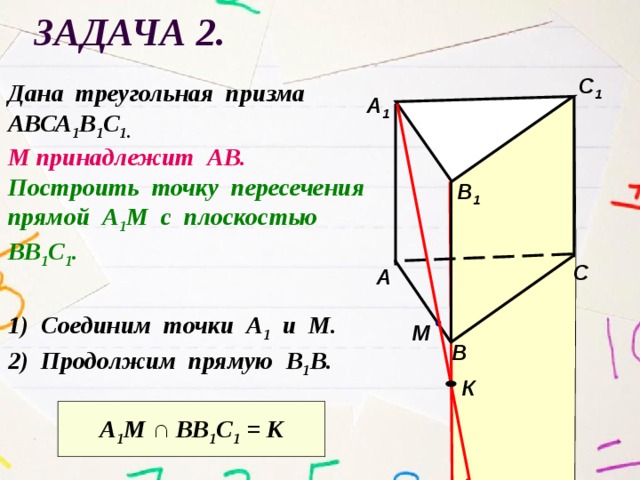
Задача 2.

С 1

Дана треугольная призма

АВСА 1 В 1 С 1.

М принадлежит АВ.

Построить точку пересечения

прямой А 1 М с плоскостью

ВВ 1 С 1 .

А 1

В 1

С

А

1) Соединим точки А 1 и М.

М

В

2) Продолжим прямую В 1 В.

К

А 1 М ∩ ВВ 1 С 1 = К

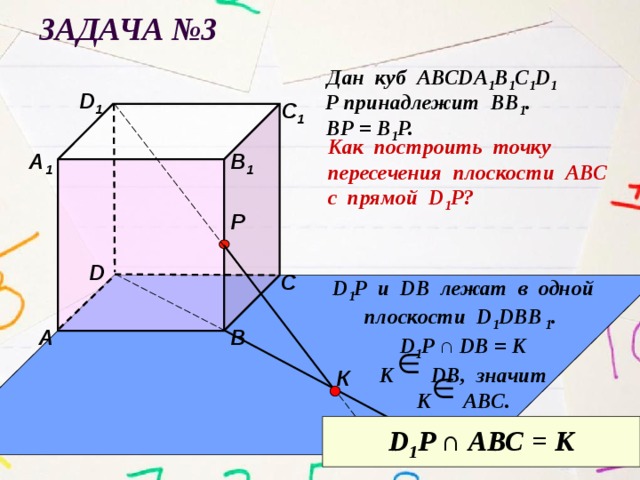
Задача №3

Дан куб АВСDА 1 В 1 С 1 D 1

D 1

Р принадлежит ВВ 1 .

С 1

ВР = В 1 Р.

Как построить точку

пересечения плоскости АВС

с прямой D 1 P?

А 1

В 1

Р

D

С

D 1 Р u DB лежат в одной

плоскости D 1 DBВ 1 .

D 1 P ∩ DB = К

К DB, значит

К АВС.

А

В

К

D 1 P ∩ АВС = К

Задача №4

Дан куб АВСDА 1 В 1 С 1 D 1

D 1

Р принадлежит ВВ 1 .

С 1

ВР = В 1 Р

Как построить линию

пересечения плоскости АD 1 Р

и АВВ 1 ?

В 1

А 1

Р

D

С

Точка Р  ВВ 1 , а значит

и плоскости АВВ 1 .

В

А

Точка А  АВ, а значит плоскости АВВ 1

Следовательно, по аксиоме А 2 , АР  АВВ 1 .

Аналогично АР принадлежит плоскости АD 1 P.

АD 1 P ∩ ABB 1 = AP

Решение задач из учебника

[6], глава 1 §2-3

№ 71, 73, 111, 112

Дополнительно №75

Самостоятельная работа

D

Дано:

Построить:

P (ADC), N (DBC)

PN∩(ABC)

Построение:

P

N

С

А

B

Викторина по истории геометрии 

1. Кто, по преданию, из великих геометров древности сказал вражескому солдату, пришедшему его убить: «Не тронь моих кругов»?

2. На каком здании были начертаны слова: «Да не войдет сюда не искусившийся в геометрии!»

3. Что, по преданию, завещал высечь на своем надгробном камне Архимед?

4. Кто является создателем первой неевклидовой геометрии? Когда и где она впервые была изложена?

5. Кто является основоположником аналитической геометрии, являющейся соединением алгебры с геометрией?

6. Кто ввел термины «абсцисса», «ордината», «координата»?

Викторина по истории геометрии 

7. Кто является автором самого первого учебника геометрии? Он же является однофамильцем известного греческого медика.

8. Этот ученый больше известен своими открытиями в алгебре, тем не менее, на своем надгробном памятнике он завещал выгравировать правильный 17-угольник, вписанный в круг. О каком ученом идет речь?

9. Назовите фамилию древнегреческого ученого, предложившего формулу для нахождения площади треугольника по трем сторонам.

10. Какая книга лежит в основе большинства школьных учебников по геометрии? Кто её автор?

11. Кто является создателем современной аксиоматики геометрии Евклида?

12. Кто автор слов «В геометрии нет особых путей для царей!»? В связи с чем они были произнесены?

Видеоролик «Евклид»

Домашнее задание

[6], глава 1 §2-3

№ 72, 74, 113

Дополнительно:

Найти ответ на вопрос

«Где в практической деятельности человека используются аксиомы стереометрии?»