Анализ информационных моделей КЕГЭ по информатике. Задание 1.Часть 1

Часть 1.

Анализ информационных моделей КЕГЭ, Задание 1.

2022

Автор: Александрова З.В., учитель физики и информатики

МБОУ СОШ №5 пгт Печенга Мурманской области

ФИПИ

Задание 1.

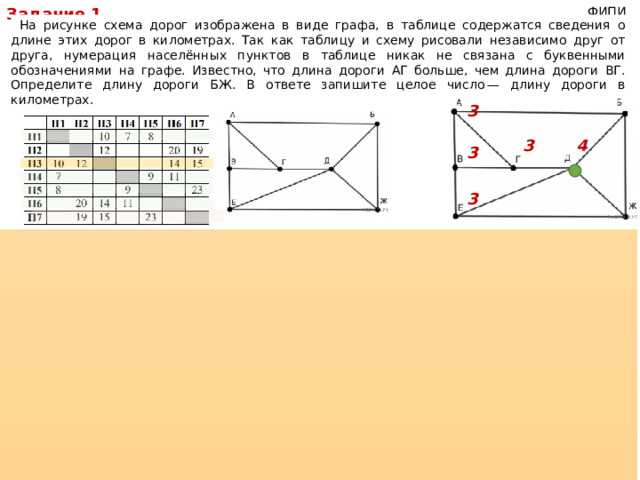
На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Известно, что длина дороги АГ больше, чем длина дороги ВГ. Определите длину дороги БЖ. В ответе запишите целое число — длину дороги в километрах.

3

4

3

3

3

• Д — единственная вершина степени 4 . Значит, Д соответствует П3.
• Вершины А и В — единственные вершины степени 3 , не связанные с вершиной Д.
• Вершины А и В соответствуют П4 и П5.
• Вершина Г — единственная вершина степени 3 , связанная и с вершинами А и В, и с вершиной Д.
• Г соответствует П1. По условию длина дороги АГ больше, чем длина дороги ВГ, значит, вершине А соответствует П5 и вершине В соответствует П4.
• Вершина Е — единственная вершина степени 3 , кроме вершины Г, связанная с вершинами В и Д. Значит, Е соответствует П6.

7. Значит, вершинам Б и Ж соответствуют П2 и П7. Найдём длину дороги БЖ по таблице, она равна 19.

Ответ: 19.

2

ФИПИ

Задание 1-1.

На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Известно, что длина дороги АГ меньше, чем длина дороги ВГ. Определите длину дороги ЕЖ. В ответе запишите целое число — длину дороги в километрах.

• Д — единственная вершина степени 4. Значит, Д соответствует П4. Заметим, что вершины А и В — единственные вершины степени 3, не связанные с вершиной Д. Значит, вершины А и В соответствуют П3 и П7.
• Вершина Г — единственная вершина степени 3, связанная и с вершинами А и В, и с вершиной Д. Значит, Г соответствует П6.
• По условию длина дороги АГ меньше, чем длина дороги ВГ, значит, вершине А соответствует П7 и вершине В соответствует П3. Вершина Е — единственная вершина степени 3, кроме вершины Г, связанная с вершинами В и Д. Значит, Е соответствует П1.
• Значит, вершинам Б и Ж соответствуют П2 и П5. Из пункта Е (П1) нет дороги в П2 и есть дорога в П5, значит, Ж — это П5. Найдём длину дороги ЕЖ (П1—П5) по таблице, она равна 24.

Ответ: 24.

ФИПИ

Задание 1-2.

На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину более короткой из дорог ГЖ и ЕИ. В ответе запишите целое число — длину дороги в километрах.

П1

П1

П2

П2

П3

16

П3

16

15

П4

П4

15

24

П5

П5

24

П6

22

22

П6

12

30

П7

30

12

П7

19

П8

П8

19

37

21

18

21

37

18

27

27

23

23

• Единственная вершина степени 7 — вершина Д, следовательно, Д соответствует П1.
• Вершина Б — единственная вершина степени 3, соединённая с двумя вершинами степени 2. Следовательно, Б соответствует П6. Тогда вершины А и В могут соответствовать П3 и П8.
• Таким образом, вершины Г и Е могут соответствовать П2 и П7, а вершины Ж и И могут соответствовать П4 и П5.
• Точное совпадение в данном случае не требуется. Длины дорог ГЖ и ЕИ равны 27 и 30. Следовательно, ответ — 27.

Ответ: 27.

Задание 1-3.

ФИПИ

• Вершина F — единственная вершина степени 2, не связанная с другими вершинами степени 2, следовательно, F соответствует П1.
• Вершина G — единственная вершина степени 3, связанная с двумя вершинами степени 2, значит, G соответствует П4.
• Тогда, поскольку B — вторая вершина степени 3, связанная с вершиной F, B соответствует П5.
• Вершина C степени 3 связана и с вершиной B, и с вершиной G, следовательно, C соответствует П2. Тогда D соответствует П3, поскольку других вершин степени 3, не соотнесённых с пунктами в таблице, не осталось.
• Окончательно, вершина A соответствует П7, а вершина E соответствует П6.

Таким образом, сумма протяжённостей дорог из пункта D в пункт B и из пункта A в пункт E равна 53 + 39 = 92.

Ответ: 92.

Задание 1-4.

ФИПИ

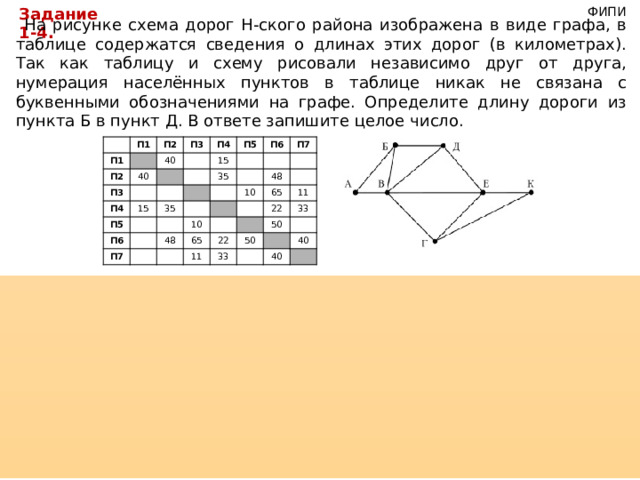
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Б в пункт Д. В ответе запишите целое число.

П1

П1

П2

П2

40

40

П3

П3

П4

П4

15

П5

П5

15

35

П6

П6

35

П7

П7

10

10

48

48

65

65

11

11

22

22

33

50

33

50

40

40

1. Есть только один пункт, из которого ведёт 5 дорог - это В, а в таблице - П6.

2. Из А ведёт две дороги и одна из них в В. В таблице такому соответствует П5.

3. Из Б ведёт 3 дороги, причём есть дороги в А и в В, в таблице под такое подходит только П3.

4. Из Д три дороги, две из которых в Б и в В, в таблице только один пункт такому соответствует - П7.Таким образом, Б - это П3, а Д - П7.

5. Длина дороги между П3 и П7 - 8.

ФИПИ

Задание 1-5.

На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Г в пункт К. В ответе запишите целое число.

П1

П1

П2

П2

П3

59

П3

59

П4

П4

24

22

П5

22

24

П5

44

П6

П6

44

П7

10

П7

27

10

27

25

25

21

21

9

9

8

8

32

32

11

11

• На карте есть только один пункт с 5 дорогами, это Г. В таблице же это П2.
• На карте есть только один пункт с 2 дорогами, это Б. В таблице же это П5.
• К - пункт, из которого выходит 3 дороги, который связан с Г, но не связан с Б. Из всех пунктов в таблице только П1 под это подходит.
• Таким образом, Г = П2, К = П1. Длина дороги между П2 и П1 - 59.

Задание 1-6.

ФИПИ

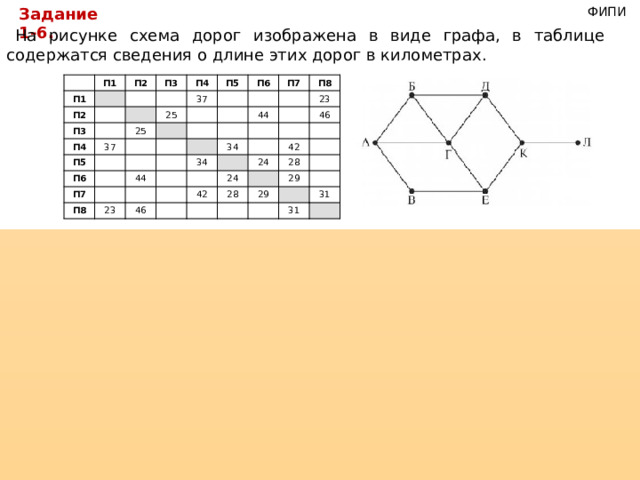
На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах.

П1

П1

П2

П2

П3

П3

П4

П4

П5

37

37

25

П5

25

П6

П6

П7

П7

П8

П8

44

44

34

23

23

34

46

46

24

42

24

42

28

28

29

29

31

31

1) Г — единственная вершина, степень которой 4, значит, Г соответствует П7.

2) Л — единственная вершина, степень которой 1, значит, Л соответствует П3.

3) К — единственная вершина, имеющая ребро с Л, значит, К соответствует П2.

4) В — единственная вершина, степень которой 2, значит, В соответствует П1.

5) Из пункта В(П1) можно идти, либо в П4, либо в П8. И из пункта К(П2) можно идти, либо в П6, либо в П8. Следовательно, Е соответствует П8, т. к. находится между В и К. А также А соответствует П4, Д соответствует П6.

6) Методом исключения найдем вершину Б — это П5.

Тогда ответ — дорога из П5 в П7, ее длина равна 28.

Ответ:28.

ФИПИ

Задание 1-7.

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.

Определите длину кратчайшего пути между пунктами A и F, проходящего через пункт E. Передвигаться можно только по указанным дорогам.

A

A

B

B

2

C

2

C

D

D

4

4

E

8

8

E

F

3

3

F

3

16

3

16

5

5

3

3

5

5

• Заметим, что в Е можно попасть только из D и F, следовательно, в маршруте также обязательно должен присутствовать пункт D.
• Составим маршрут следующим образом: стартуя из пункта А, будем всегда выбирать тот пункт, расстояние до которого наименьшее. Получим маршрут A—B—D—E—F, его длина равна 2 + 3 + 5 + 5 = 15 км.
• Теперь, начиная с начала маршрута, будем изменять путь, пользуясь следующим соображением: если расстояние, например, A—B—D больше расстояния A—D, то заменяем участок маршрута A—B—D на A—D.
• Попробовав произвести все такие замены, получим, что маршрут A—B—D—E—F — самый короткий из тех, что удовлетворяют условию задачи.
• Любое другое изменение пути, через которые проходит маршрут, приводит к увеличению его длины.

Ответ: 15.

Задание 1-8.

ФИПИ

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.

Определите длину кратчайшего пути между пунктами A и F, проходящего через пункт E и не проходящего через пункт B. Передвигаться можно только по указанным дорогам.

A

A

B

B

C

C

2

2

4

D

4

D

8

E

8

E

3

3

F

F

16

3

3

16

2

2

3

3

5

5

Найдём все варианты маршрутов, удовлетворяющих условию и выберем самый короткий.

A−C−D−E−F. Длина маршрута 4 + 3 + 2 + 5 = 14.

A−D−E−F. Длина маршрута 8 + 2 + 5 = 15.

Кратчайший путь равен 14.

Ответ: 14.

Задание 1-9.

ФИПИ

Между населенными пунктами  A ,  B ,  C ,  D ,  E ,  F  построены дороги, протяженность которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.

Определите длину кратчайшего пути между пунктами  A  и  F  (при условии, что передвигаться можно только по построенным дорогам).

A

A

B

B

4

C

4

C

7

D

D

7

E

11

E

11

6

F

F

6

5

16

16

5

3

9

9

3

4

4

Варианты маршрутов:

A-B-D-E-F. Длина маршрута 4 + 6 + 3 + 4 = 17

A-B-E-F. Длина маршрута 4 + 5 + 4 = 13

A-C-F. Длина маршрута 7 + 9 = 16

A-F. Длина маршрута 16

Видно, что кратчайший путь равен 13.

Ответ: 13.

ФИПИ

Задание 1-10.

Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.

Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам).

A

A

B

B

2

C

2

C

D

D

10

10

E

E

9

9

F

6

6

F

3

G

3

G

6

6

9

5

5

9

14

14

7

7

Рассмотрим все возможные маршруты. Кратчайшим окажется A-B-E-F-G длиной 17

Использованные источники:

https://inf-ege.sdamgia.ru/test?id=9415198

https://kpolyakov.spb.ru/school/ege.htm

https://vpr-ege.ru/ege/informatika/1665-trenirovochnye-varianty-ege-2022-po-informatike

https://4ege.ru/informatika/62626-demoversija-ege-2022-po-informatike.html

https://labs-org.ru/ege-demo2022/

https://ctege.info/ege-po-informatike/otkryityiy-variant-ege-2022-po-informatike.html