Арифметический корень натуральной степени

Поворот точки вокруг начала координат

Тема урока:

Арифметический корень натуральной степени

Учитель математики МБОО СОШ № 10 г. Лобня Х.И. Мартиросян

ЦЕЛИ УРОКА

• дать понятие корня n-й степени

• дать понятие арифметического корня n-й степени

• определить свойства корня n-й степени

• закрепить понятия, выполнив задания

Вычислите, представьте в виде степени или упростите, если возможно:

Вычислите, представьте в виде степени или упростите, если возможно:

Вычислите, представьте в виде степени или упростите, если возможно:

Вычислите, представьте в виде степени или упростите, если возможно:

21.09.2016

Тема урока:

Арифметический корень натуральной степени.

Учитель математики МБОО СОШ №10 г. Лобня Х.И. Мартиросян

Алгебраический словарь:

Квадратным корнем из числа а называется такое число, квадрат которого равен а

Корнем п –й степени из числа а называется такое число, п – ая степень которого равна а

Таблица степеней:

5 1 =5

4 1 =4

2 6 =64

2 1 =2

3 1 =3

4 2 =16

3 2 =9

5 2 =25

2 7 =128

2 2 =4

3 3 =27

4 3 =64

5

5 3 =125

5 3

2 8 =256

2 3 =8

4 4 =256

3 4 =81

5 4 =625

2 4 =16

2 9 =512

2 5 =32

6 1 =6

2 10 =1024

3 5 =243

7 1 =7

6 2 =36

7 2 =14

Примеры:

7 3 =343

6 3 =216

3

3

=

=

125

3

343

5

243

Устно:

3

9

216

512

}

Правила взаимного исключения :

I

n

(

)

n

=

имеет смысл

n-нечетное : a  R

a ≥0

n-четное :

II

a

2

n

a

1

2

+

n

1

2

+

n

n

2

=

=

a  R

имеют смысл:

Имеют ли смысл выражения:

корень нечетной степени существует из любого числа

корень четной степени определен только для неотрицательного числа

Найти область определения выражения:

.

При каких значениях х имеет смысл выражения:

Способы извлечения квадратных корней:

• По таблице

2. Алгебраический;

3. Древневавилонский:

Пример:

Выполни по образцу:

Извлечение корней третьей степени.

Подсказка.

Образец.

Реши сам:

Вычислить:

Формула:

Образец.

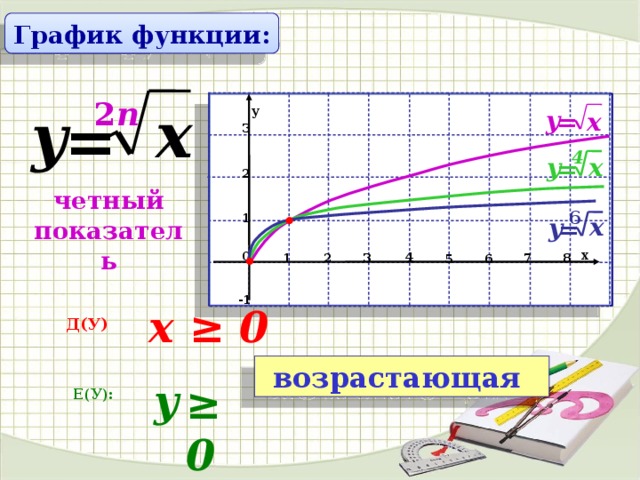
График функции:

2

n

x

y

=

y

y

x

=

3

4

y

x

=

2

четный показатель

1

6

x

y

=

0

4

2

3

1

x

6

5

8

7

-1

x ≥ 0

Д(У)

возрастающая

y

≥ 0

Е(У):

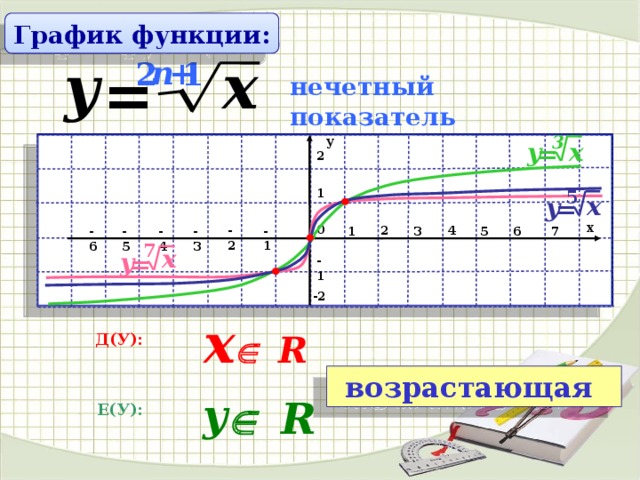
График функции:

x

y

+

n

1

2

=

нечетный показатель

3

y

x

y

=

2

1

5

x

y

=

0

-2

4

2

-1

-5

-4

-6

-3

x

3

6

1

5

7

7

x

y

=

-1

-2

x  R

Д(У):

возрастающая

 R

y

Е(У):