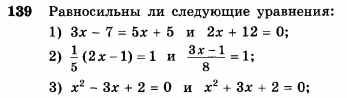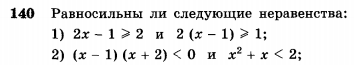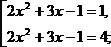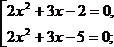832, 16.04.2020 "Равносильность уравнений и неравенств. Основные приемы решения рациональных уравнений."

Равносильность уравнений и неравенств.

Основные приемы решения рациональных уравнений.

Многие уравнения с помощью различных приемов, выполнив подходящие замены переменных, можно свести к квадратным. Вспомним некоторые из них.

1) 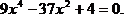  Такое уравнение называется биквадратным.

Замена: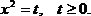 
 D = 1225 =  ,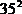     

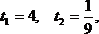
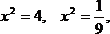
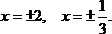
Ответ: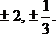 

2) 

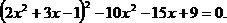
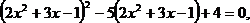
Замена: 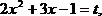  тогда получим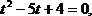   

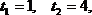
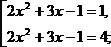
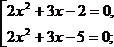
Ответ: –2,5, –2, 0,5, 1.

3) В уравнении  , перемножая попарно скобки, получим   Сделав замену   сводим уравнение к квадратному.

4)   О.Д.З.: 

Замена:   тогда     получаем   
 т.к. х 0, то получаем   

Ответ: –1, –2, 

5) Симметрическим уравнением называется уравнение вида   где  Заметим, что симметрическое уравнение нечетной степени имеет корень х = –1, симметрическое уравнение четной степени можно решить, используя замену   В школьном курсе математики часто встречаются симметрические уравнения четвертой степени, которые в общем виде можно записать так:   где
Решим уравнение   О.Д.З.:  R.
Заметим, что х = 0 не является корнем уравнения, поэтому, разделив обе части уравнения на  , получим уравнение   
Пришли к уравнению, решение которого рассмотрено в п.4.

6) Возвратным уравнением нечетной степени называется уравнение вида   где  R.

Возвратное уравнение четной степени – это уравнение вида   где  R.

Заметим, что возвратное уравнение нечетной степени имеет корень 

Решим возвратное уравнение четверной степени 
О.Д.З.:  R. Заметим, что   Разделив обе части уравнения на  ( , получим   
Замена :   тогда 
   

Ответ: 

7) Однородным уравнением  ой степени называется уравнение вида   которое заменой   сводится к алгебраическому уравнению  ой степени.

Решим уравнение, которое сводится к однородному уравнению четвертой степени:

 О.Д.З.: R.
 Заметим, что  , поэтому можем разделить обе части уравнения на выражение  , получим
, это уравнение заменой   сводится к квадратному уравнению 

Рассмотрим еще некоторые уравнения, сводящиеся к квадратным.
8)  О.Д.З.:  R.
Заметим, что х = 0 не является корнем уравнения, поэтому можем разделить обе части его на   получим   

Замена:   Получаем квадратное уравнение   

При решении последних уравнений мы пользовались утверждением: при умножении или делении обеих частей уравнения на число или выражение, не равное нулю на области допустимых значений переменной, получаем уравнение, равносильное данному.

Можно использовать и другое утверждение: при делении числителя и знаменателя дроби на число или выражение, не равное нулю на области допустимых значений переменной, получаем уравнение, равносильное данному. Покажем, как используется это утверждение.

9)   О.Д.З.:  R 

Заметим, что х = 0 не является корнем уравнения, поэтому, разделив числитель и знаменатель каждой дроби на х, получим   Замена:   тогда   

10) При решении уравнения вида   можно воспользоваться заменой

Решим уравнение:   Сделаем замену:     получим         

Ответ: –5, 1.

11) Рассмотрим метод выделения полного квадрата при решении рационального уравнения.

 О.Д.З.:
 
 

Выполнив замену   получим квадратное уравнение 

12) Покажем, как при решении уравнений может значительно упростить решение выделение целой части дробного выражения.

 О.Д.З.: 

Выделять целую часть можно делением «уголком» числителя на знаменатель или, например, следующим образом:   Выполняя аналогичные преобразования каждой дроби, получим 
   замена: 

Ответ: 

Задание для выполнения: С целью закрепления навыков решения уравнений рассмотренными методами, решите следующие уравнения (достаточно любые 3).

1)
2) 
3) 
4) 
5) 

6) 
7) 
8)