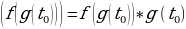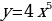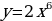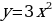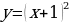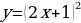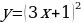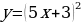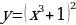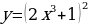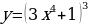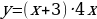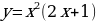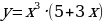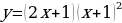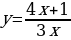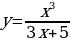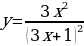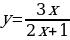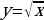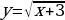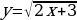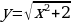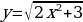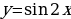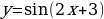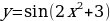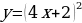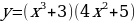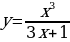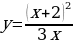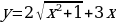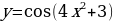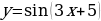Тема 3. Дифференциальное исчисление
Технологическая карта № 1-2
Дисциплина: «Элементы высшей математики»
Специальность: 09.02.07 Информационные системы и программирование
Курс: 2 Группа: _____ Дата проведения:_______
Тема: Определение производной и дифференциала. Производные высших порядков
Цели занятия:
Дидактическая (обучающая):
- создать условия для формирования представления о дифференциальном исчислении, знакомства с необходимыми формулами дифференциального исчисления, умения решать задачи, связанные с изучаемыми понятиями.
Воспитательная:
- создать условия для воспитания сознательности, ответственности за повышения своего уровня образования.
Развивающая:
- создать условия для развития внимания, памяти, воображения, воли, логического мышления;
Вид занятия: лекция.
Тип занятия: комбинированный
Методы занятия:
- развивающие (объяснение, разъяснение, рассказ, беседа (вводная, эвристическая), лекция, метод дедукции, метод индукции);
- наглядные (показ, демонстрация);
- практические (упражнения (воспроизводящие, тренировочные), решение проблемных ситуаций)
Межпредметные связи:
обеспечивающие: связь теории с практикой решения задач.
обеспечиваемые: школьным курсом математики
Оборудование и методическое обеспечение урока: раздаточный материал.
Студент должен в соответствии с ФГОС СПО:
ОК 1 Выбирать способы решения задач профессиональной деятельности, применительно к различным контекстам,
ОК 5 Осуществлять устную и письменную коммуникацию на государственном языке с учетом особенностей социального и культурного контекста.
Литература:
Григорьев, В. П. Элементы высшей математики [Текст] : учебник для использования в учебном процессе образовательных учреждений, реализующих программы СПО по укрупненной группе специальностей "Информатика и вычислительная техника", ЕН.01 "Элементы высшей математики" / В. П. Григорьев, Ю. А. Дубинский, Т. Н. Сабурова. – М. : Академия, 2016. – 399 с.
Григорьев, В. П. Сборник задач по высшей математике: Учеб. пособие для студентов учрежд. СПО / В. П. Григорьев, Т. Н. Сабурова. – М. : Академия, 2014. – 160 с.
Ход занятия
| №
| Элементы занятия | Время, минут | Методы |
| 1 | Организационная часть | 1 |
|
| 2 | Мотивация учебной деятельности | 1 | информационно-развивающие; |
| 3 | Сообщение темы, цели задач занятия | 1 | информационно-развивающие; |
| 4 | Актуализация опорных знаний студентов - Беседа. Что такое производная? - Какие формулы нахождения производной помните? | 5 | информационно-развивающие; |
| 5 | Введение нового учебного материала Понятие производной. Правила дифференцирования функции. Производные элементарных функций. Производная сложной функции. | 25 | информационно-развивающие; - наглядные; практические |
| 6 | Осмысление учебного материала Решение задач № 1-6 | 45 | наглядные; практические |
| 7 | Обобщение и систематизация знаний Решение задач: y=(5х7+3)4 , y=(х+3)(2х+1)2 Обсудить использование правил и формул
| 10 | наглядные; практические |
| 8 | Подведение итогов
| 1 | информационно-развивающие; |
| 9 | Задание для самостоятельного рассмотрения Задачи; 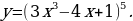 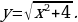 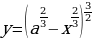 . . 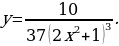 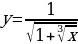
| 1 | информационно-развивающие; |
I Организационная часть
II Мотивация учебной деятельности
При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом 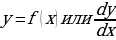
При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Её решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления. Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И. Ньютона и Г.В. Лейбница, который использовал понятие бесконечно малой. Ньютон пришёл к открытию дифференциального исчисления при решении задач о скорости движения материальной точки в данный момент времени (мгновенной скорости).
Производную применяют для исследования функции и построения ее графика, для нахождения наибольшего и наименьшего значений функции.
Производная нужна также и с в экономике. В экономической теории активно используется понятие «маржинальный», что означает «предельный». Введение этого понятия в научный оборот в XIX веке позволило создать совершенно новый инструмент исследования и описания экономических явлений - инструмент, по средством которого стало возможно ставить и решать новый класс научных проблем.
Производная выступает как интенсивность изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора.
III. Сообщение темы, цели задач занятия: Дифференциальное исчисление
IV. Актуализация опорных знаний студентов
Беседа
Введение нового учебного материала
1. Понятие производной, дифференциала.
2. Правила дифференцирования функции.
3. Производные элементарных функций.
4. Производная сложной функции.
Осмысление учебного материала
Решение задач № 60 (1 – 6)
Обобщение и систематизация знаний
Подведение итогов
Задание для самостоятельного рассмотрения
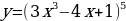
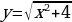
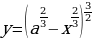 .
.
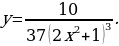
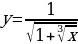
III. Информационная часть
Понятие производной
Рассмотрим задачу, приводящую к понятию производной: задачу о скорости движущейся точки.
Пусть S=S(t) – закон движения материальной точки.
∆S – путь, пройденный за промежуток времени ∆t.
Следовательно 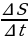 – средняя скорость.
– средняя скорость.
При ∆t→0 (т.е. чем короче промежуток времени, тем лучше, точнее, средняя скорость) средняя скорость лучше характеризует движение точки в фиксированный момент времени.
Если мы говорим о ∆t→0, то тем самым фиксируем предельное ее значение, поэтому здесь имеет место понятие предела: 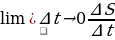 , но мы знаем, что отношение является средней скоростью, следовательно
, но мы знаем, что отношение является средней скоростью, следовательно 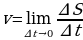 – такая величина в математике носит название производной:
– такая величина в математике носит название производной:
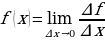
Производная функции – понятие дифференциального исчисления, характеризующее скорость изменения функции в этой точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
Дифференциалом функции в точке называют главную, линейную относительно часть ее приращения которая равна произведению производной функции в этой точке на приращение аргумента: Замечание. Дифференциал называют также дифференциалом первого порядка.
Рассмотрим функцию 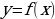 , которая имеет конечную производную
, которая имеет конечную производную 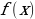 в некотором интервале
в некотором интервале 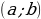 , то есть производная
, то есть производная 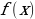 также является функцией переменной
также является функцией переменной 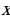 в этом интервале. Если эта функция дифференцируема, то мы можем найти вторую производную исходной функции
в этом интервале. Если эта функция дифференцируема, то мы можем найти вторую производную исходной функции
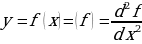
То есть вторая производная есть первой производной от первой производной.
Аналогично, если производная 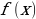 существует и дифференцируема, то можно найти третью производную рассматриваемой функции:
существует и дифференцируема, то можно найти третью производную рассматриваемой функции:
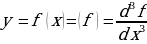
Таким образом, понятие производной n-го порядка вводится индуктивно путем последовательного вычисления n производных, начиная с производной первого порядка. Переход к производной следующего, более высокого порядка производится с помощью рекуррентной формулы: :
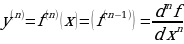
Замечание. Порядок производной, чтобы не путать с показателем степени, пишут в круглых скобках либо записывают римскими цифрами. Например, производная четвертого порядка
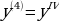
При нахождении производных высшего порядка используются следующие соотношения:
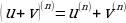
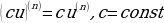
Правила дифференцирования функций
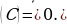
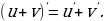
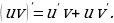
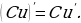
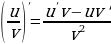
Производные элементарных функций
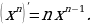
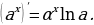
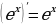
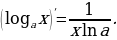
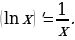
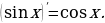
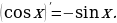
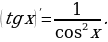
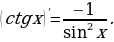
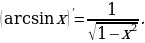
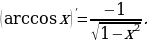
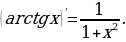
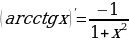
Производная сложной функции
Если f(x) имеет производную в точке 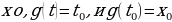 , тогда производная сложной функции
, тогда производная сложной функции 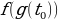 находится по формуле:
находится по формуле:
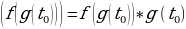
Говорим: производная сложной функции равна производной самой функции, умноженной на производную аргумента.
Упражнения
№ 1
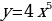
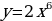
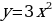
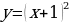
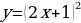
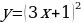
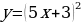
№ 2
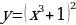
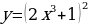
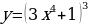
№ 3
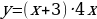
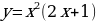
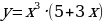
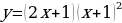
№ 4
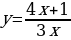
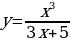
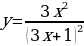
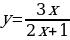
№ 5
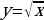
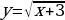
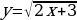
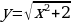
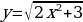
№ 6
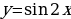
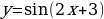
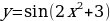
Самостоятельная работа – обучающая.
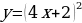
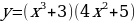
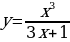
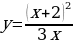
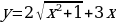
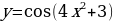
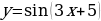
Раздаточный материал к занятию
Правила дифференцирования и производные основных элементарных функций
Правила дифференцирования функций
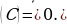
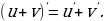
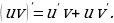
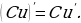
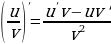
Производные элементарных функций
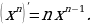
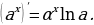
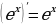
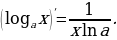
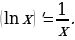
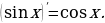
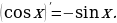
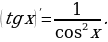
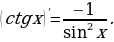
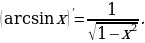
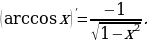
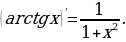
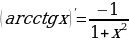
Задание для самостоятельного рассмотрения
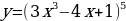
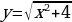
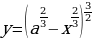 .
.
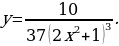
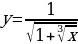







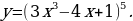
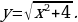
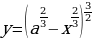 .
. 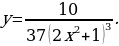
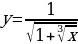
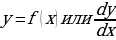
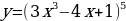
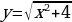
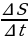 – средняя скорость.
– средняя скорость.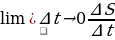 , но мы знаем, что отношение является средней скоростью, следовательно
, но мы знаем, что отношение является средней скоростью, следовательно 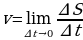 – такая величина в математике носит название производной:
– такая величина в математике носит название производной: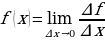
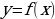 , которая имеет конечную производную
, которая имеет конечную производную 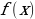 в некотором интервале
в некотором интервале 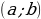 , то есть производная
, то есть производная 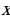 в этом интервале. Если эта функция дифференцируема, то мы можем найти вторую производную исходной функции
в этом интервале. Если эта функция дифференцируема, то мы можем найти вторую производную исходной функции 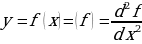
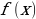 существует и дифференцируема, то можно найти третью производную рассматриваемой функции:
существует и дифференцируема, то можно найти третью производную рассматриваемой функции: 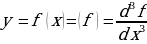
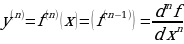
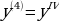
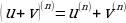
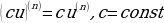
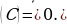
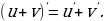
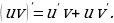
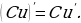
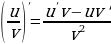
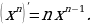
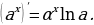
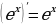
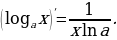
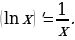
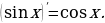
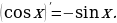
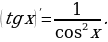
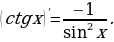
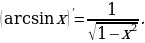
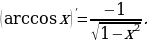
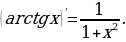
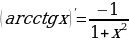
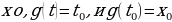 , тогда производная сложной функции
, тогда производная сложной функции 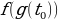 находится по формуле:
находится по формуле: