Функция и ее свойства

Функция у = х п и ее свойства.

МБОУ СОШ №4

Повторение:

• Какое выражение надо подставить вместо * , чтобы получилось тождество:

х 4

х 3

3.

1.

х 10

х 4

4.

2.

Повторение:

х 7

• Упростите:

1/а

х 9

16 b 2

р 15

-1/2а

1

1/25

8000

у = х п - степенная функция , где х – независимая переменная, п – натуральное число.

п = 1

у = х – линейная

функция

D y = R

Е х = R

у = х – прямая

пропорциональность

Нечетная.

Возрастает на ( -∞ ; +∞ )

х = 2; у = 2

у = х п

п = 2

у = х 2 – квадратичная

функция

Е у = [ 0 ; +∞ )

D y = R

Четная. ( График

симметричен относительно Оу )

Убывает на ( -∞ ; 0 ]

х

0

у

1

0

2

1

4

Возрастает на [ 0 ; +∞ )

0. График функции расположен в I и II координатных четвертях. у( -х ) = ( -х ) 2 k = х 2 k = у( х ) – четная. График функции симметричен относительно оси ординат. Функция возрастает в промежутке [ 0 ; +∞ ) и убывает в промежутке ( -∞; 0 ] . Е х = [ 0 ; +∞ ) Проходит ли график функции через начало координат? В каких четвертях будет расположен график функции? Определите, функция четная или нечетная. На каких промежутках функция возрастает? Убывает? Какова область значений функции? " width="640"

Свойства степенной функции у = х п при п = 2 k.

• y = х 2 k ; D y = R
• При х = 0 у = 0. График функции проходит через начало координат.
• При х ≠ 0 у 0. График функции расположен в I и II координатных четвертях.
• у( -х ) = ( -х ) 2 k = х 2 k = у( х ) – четная. График функции симметричен относительно оси ординат.
• Функция возрастает в промежутке [ 0 ; +∞ ) и убывает в промежутке ( -∞; 0 ] .
• Е х = [ 0 ; +∞ )

Проходит ли график функции через начало

координат?

В каких четвертях будет расположен график

функции?

Определите, функция четная или нечетная.

На каких промежутках функция возрастает?

Убывает?

Какова область значений функции?

График степенной функции с четным показателем.

0 ( I u II ч.) у( -х ) = (-х) 4 = х 4 = у(х). Функция четная. Ф – ция убывает в ( -∞ ; 0 ] Возрастает в [ 0 ; +∞ ). х у -2 -1 16 0 1 1 0 1 2 16 " width="640"

Построить график функции у = х 4 .

• D y = R
• х = 0, у = 0.
• х ≠ 0, у 0 ( I u II ч.)
• у( -х ) = (-х) 4 = х 4 = у(х). Функция четная.
• Ф – ция убывает в ( -∞ ; 0 ] Возрастает в [ 0 ; +∞ ).

х

у

-2

-1

16

0

1

1

0

1

2

16

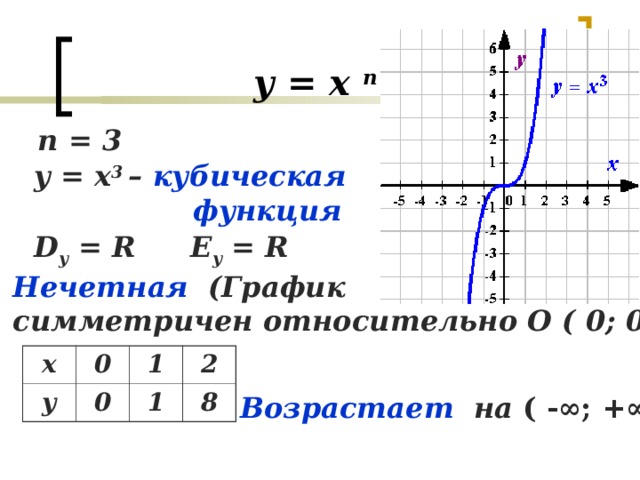
у = х п

n = 3

y = x 3 – кубическая

функция

D y = R

E y = R

Нечетная (График

симметричен относительно О ( 0; 0 ))

х

0

у

1

0

2

1

8

Возрастает на ( -∞; +∞ )

0, то у 0; если х 0, то у 0. График функции расположен в I u III координатных четвертях . у(-х) = (-х) 2 k+1 = -x 2k+1 = -y(x) . Функция нечетная. График симметричен относительно начала координат. Функция возрастает на всей области определения. Е х = R Проходит ли график функции через начало координат? В каких координатных четвертях будет расположен график функции? Определите, функция четная или нечетная. На каких промежутках функция возрастает? Убывает? Какова область значений функции? " width="640"

Свойства степенной функции у = х п при п = 2 k + 1 .

• y = х 2 k +1 ; D y = R
• При х = 0 у = 0. График функции проходит через начало координат.
• Если х 0, то у 0; если х 0, то у 0. График функции расположен в I u III координатных четвертях .
• у(-х) = (-х) 2 k+1 = -x 2k+1 = -y(x) . Функция нечетная. График симметричен относительно начала координат.
• Функция возрастает на всей области определения.
• Е х = R

Проходит ли график функции через начало

координат?

В каких координатных четвертях будет

расположен график функции?

Определите, функция четная или нечетная.

На каких промежутках функция возрастает?

Убывает?

Какова область значений функции?

График степенной функции с нечетным показателем.

Решение примеров:

• № 504 ( устно )
• № 505 ( устно )
• № 494
• № 496 ( б, в )
• № 497 ( б, в )

Домашнее задание:

• п.22, №№ 495; 503; 507.

Функция у = х п . II часть.

• Сколько корней имеет уравнение х п = 10 при п – четном? п – нечетном?
• Какие из графиков функций имеют центр симметрии; ось симметрии?

Центр симметрии

Ось симметрии

а) б) в) г) " width="640"

Сравните:

a)

• f ( x ) = x 10
• f ( x ) = x 9

б)

в)

=

г)

а)

б)

в)

г)

Найдите ошибку:

1.

2.

3.

Решите уравнения:

Ответ:

1.

Ответ:

2.

3.

Корней нет

Ответ:

4.

Ответ:

Ответ:

5.

Самостоятельная работа: I вариант. II вариант.

1. Сколько корней имеет уравнение при четном п; при нечетном п?

х п = 25

х п = 15

2. Решите уравнения:

а) х 3 = -27;

б) х 4 = -81;

в) х 4 = 256.

а) х 3 = - 64;

б) х 4 = 36;

в) х 4 = 81.

3. Сравните:

а) 1,4 80 и 1,3 80 ;

б) ( -80) 4 и ( -78) 4 ;

в) ( -23) 6 и 18 6 .

а) 1,2 30 и 1,5 30 ;

б) ( -27) 6 и ( -30) 6 ;

в) ( -18) 24 и 6 24 .

До новых встреч!