Интеграл. Формула Ньютона-Лейбница.

Интеграл. Формула Ньютона – Лейбница.

составитель: преподаватель математики

Цель урока:

• Ввести понятие интеграла и его вычисление по формуле Ньютона – Лейбница, используя знания о первообразной и правила её вычисления;

• Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции;

• Закрепить изученное в ходе выполнения упражнений.

Определение:

Пусть дана положительная функция f(x) , определенная на конечном отрезке [a;b].

Интегралом от функции f(x) на [a;b] называется площадь её криволинейной трапеции.

y

y=f(x)

x

a

0

b

3

Обозначение:

 «интеграл от a до b эф от икс дэ икс»

3

Историческая справка:

Обозначение интеграла Лейбниц произвёл от первой буквы слова «Сумма» (Summa). Ньютон в своих работах не предложил альтернативной символики интеграла, хотя пробовал различные варианты. Сам термин интеграл придумал Якоб Бернулли.

Готфрид Вильгельм

фон Лейбниц

S umma

Якоб Бернулли

Исаак Ньютон

5

Оформление определённого интеграла в привычном нам виде придумал Фурье.

Обозначение неопределённого интеграла ввёл Эйлер.

Леонард Эйлер

Жан Батист Жозеф Фурье

6

Формула Ньютона - Лейбница

6

Пример 1.

Вычислить определённый интеграл:

Решение:

=

6

Пример 2.

Вычислите определённые интегралы:

5

9

1

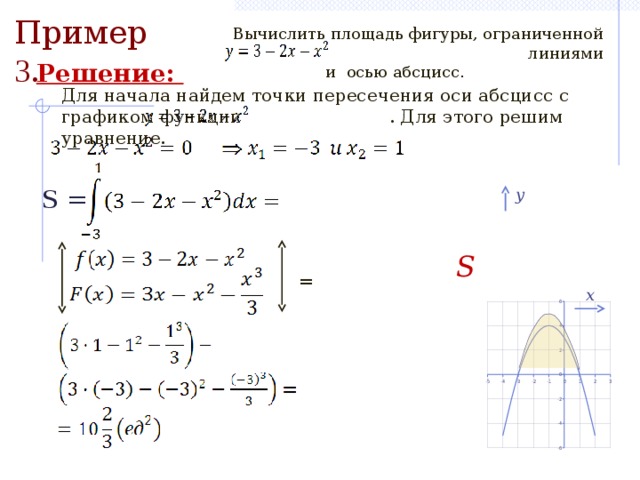
Пример 3 .

Вычислить площадь фигуры, ограниченной линиями

и осью абсцисс.

Решение:

Для начала найдем точки пересечения оси абсцисс с графиком функции . Для этого решим уравнение.

S =

y

S

=

x

10

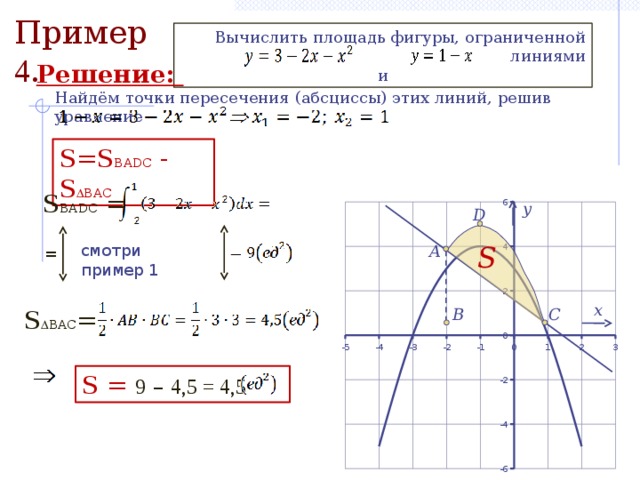
Пример 4 .

Вычислить площадь фигуры, ограниченной линиями

и

Решение:

Найдём точки пересечения (абсциссы) этих линий, решив уравнение

S=S BADC - S  BAC

S BADC =

y

D

S

смотри пример 1

A

=

x

S  BAC =

B

C

S = 9 – 4,5 = 4,5

11

ПРАВИЛА СИНКВЕЙНА

1строка – тема синквейна 1 слово

2строка – 2 прилагательных, описывающих признаки и свойства темы

3строка – 3 глагола описывающие характер действия

4строка – короткое предложение из 4 слов, показывающее Ваше личное отношение к теме

5строка – 1 слово, синоним или Ваша ассоциация тема предмета.

11

• Интеграл

2. Определённый, положительный

• Считают, прибавляют, умножают

4. Вычисляют формулой Ньютона - Лейбница

5. Площадь

11

« ТАЛАНТ –

это 99% труда и 1% способности»

народная мудрость

Спасибо за внимание!

11

Пример 1.

Вычислить определённый интеграл:

Решение:

=

пример 4

11