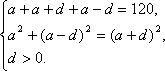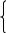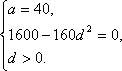Использование современных информационных технологий при подготовке к итоговой аттестации по теме «Решение задач на геометрическую (арифметическую) прогрессию с применением математического моделирования».
Содержание
| 1. Последовательности и прогрессии в школьном курсе алгебры 9-го класса, отработка заданий темы при подготовке к ГИА по математике. |
|
| 2. Диагностика ошибок: основные недостатки подготовки учащихся по блоку «Последовательности и прогрессии». 3. Методические рекомендации. Основные методы решения задач на прогрессии (в том числе с помощью систем уравнений). 4. Фрагмент урока повторения и обобщения изученных методов решения задач на арифметическую прогрессиюс использованием ИОР. 5. Приложение. |
|
1. Последовательности и прогрессии в школьном курсе алгебры 9-го класса, отработка заданий темы при подготовке к ГИА по математике.
Государственная итоговая аттестация дает большие возможности для диагностики учебных достижений учащихся. По отношению к конкретному ученику итоговая аттестация позволяет решать три основные задачи:
Выявление конкретных недостатков в знаниях и умениях учащихся;
Определение уровня его математической компетентности;
Выявление готовности к обучению к старшей школе.
Задания блока «Последовательность и прогрессии направлены на проверку владения следующими знаниями и умениями:
знать и понимать термины «последовательность», «член последовательности», «n-й член последовательности», «арифметическая прогрессии», «геометрическая прогрессия»;
понимать и использовать индексные обозначения;
находить члены последовательности, заданной формулой n-го члена или рекуррентным способом;
распознавать арифметические и геометрические прогрессии при различных способах задания, переходить от одного способа задания прогрессии к другому;
применять формулы n-го члена и суммы первых n-х членов «арифметической и геометрической прогрессий для решения не сложных задач, в том числе на жизненной практики.
2.Диагностика ошибок: основные недостатки подготовки учащихся по блоку «Последовательности и прогрессии».
Учащиеся не владеют индексными обозначениями,
не могут перевести на естественный язык рекуррентное соотношение.
Они усваивают тему формально, не овладевая, ее общеобразовательной составляющей. При этом одним из результатов изучения темы должно быть понимание того, что, зная первый член последовательности, можно по известному правилу найти второй член; зная второй член, можно точно также найти третий и т.д.,
Одна из причин возникающих пробелов – рекуррентные формулы рассматриваются мимоходом и достаточно формально, они не осознаются школьниками как символическая запись вычислительного алгоритма.
У учащихся стабильно возникают трудности в тех случаях, когда от них требуется перейти с одного математического языка на другой или речь идет о некоторой интерпретации. Большие трудности вызывает задача, связанная с пониманием представления членов арифметической прогрессии точками на координатной плоскости.
Одной из причин возникающих трудностей является узкий отбор учебного материала, состоящего преимущественно из стандартных задач. В результате учащиеся не осознают сущностные аспекты содержания данного вопроса, затруднен перенос задания на аналогичную, но все же новую ситуацию. Учащиеся ориентируются не на существенные, основополагающие отношения, а на внешние ситуативные.
Рассмотрим примеры заданий повышенного уровня трудности. Они содержатся во второй части экзаменационной работы. Выполняют их учащиеся, имеющие хорошую математическую подготовку.
Найдите сумму всех натуральных чисел, не превосходящих 150, которые не делятся на 3.
Ученик должен, прежде всего, распознать арифметическую прогрессию, а затем применить формулу суммы первых n членов арифметической прогрессии для суммирования натуральных чисел и чисел, кратных 3.
При решении учащиеся должны сделать логический шаг: чтобы найти сумму чисел, не делящихся на 3, надо найти сумму всех натуральных чисел до заданного числа включительно и вычесть из нее сумму тех чисел, которые делятся на 3. Этот логический прием применяется при решении многих задач повышенного уровня, и обучение математике обязано формировать у сильных учащихся соответствующее умение. Никакими специальными приемами для решения подобной задачи владеть не надо, все необходимые фактические знания учащиеся получают в общем курсе алгебры основной школы.
Рассмотрим еще два задания из второй части работы.
Найдите сумму всех отрицательных членов арифметической прогрессии --8,6;-8,4;…
| В геометрической прогрессии сумма первого и второго членов равна 108, а сумма второго и третьего членов равна 135.Найдите первые три члена этой прогрессии.
Из этих двух заданий на арифметическую и геометрическую прогрессии более трудным для учащихся оказалось первое .Хотя задания. связанные с арифметической прогрессией, решаются учащимися лучше и охотнее, чем с геометрической, что связано с характером вычислений.
Условие первого задания носит содержательный характер, поскольку предложенную арифметическую прогрессию надо сначала самостоятельно задать формулой n-го члена, а условие второго задания- более формальное, так как можно сразу применять известные формулы. Содержательное для учащихся кажется труднее формального.
3. Основные методы решения задач на прогрессии (в том числе с помощью систем уравнений).
1. Все данные выражаются через первый член и разность (знаменатель) прогрессии и далее решается система уравнений.
2. Более короткие решения получаются при использовании формулы для выражения аk через равностоящие члены, т.е. аk-s и ak+s.
Приведенные примеры повышенного уровня, соответствуют заданиям второй части итоговой аттестации.
Пример 1. В геометрической прогрессии сумма первого и второго членов равна 132, а сумма второго и третьего членов равна 110. Найдите первые три члена этой прогрессии.
Решение. Пусть (bn) – данная геометрическая прогрессия. По формуле n - го члена геометрической прогрессии bn=b1*qn-1, где b1 – первый член прогрессии, q – ее знаменатель, выразим данные члены прогрессии: b2=b1q, b3=b1q2.
Составим и решим систему уравнений:
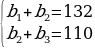
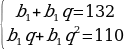
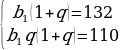
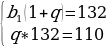
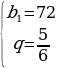
B2 =72*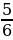 =60, b3 =60*
=60, b3 =60*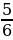 =50
=50
Ответ: 72; 60; 50
Другое решение : Пусть (b1) – данная геометрическая прогрессия.
По свойству геометрической прогрессии b1b3=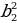 . По условию задачи:
. По условию задачи:
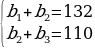 откуда
откуда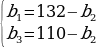
Перемножив, получаем: b1b=(132-b2)(110-b2)
Полученное уравнение перепишем в виде: 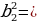 )*(110 – b2)
)*(110 – b2)
Полученное уравнение перепишем в виде: 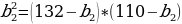 или
или
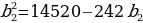 откуда b2 = 60. Тогда b1 = 72, b3 = 50
откуда b2 = 60. Тогда b1 = 72, b3 = 50
Ответ: 72; 60; 50
Пример 2.
Найти сумму всех натуральных чисел, не превосходящих 160, которые не делятся на 4.
Решение:
Найдем сумму всех натуральных чисел, не превосходящих 160. 1; 2;3;...-арифметическая прогрессия: a1=1, d=1.
S160=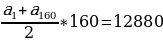 .
.
Найдем сумму всех натуральных чисел, кратных 4 и не превосходящих 160. Последовательность (bn) чисел, кратных 4, задается формулой bn=4n. (bn) – арифметическая прогрессия с b1=4, d=4; bn=160, n=40.
S40=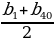 40, S40=
40, S40=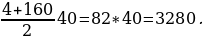
Найдем сумму всех натуральных чисел, не превосходящих 160, которые не делятся на 4. Эта сумма равна сумме всех натуральных чисел, не превосходящих 160, без суммы натуральных чисел, кратных 4.
12880-3280=9600.
Ответ: 9600.
Пример 3.Найдите сумму всех натуральных чисел, не превосходящих 200, которые не делятся на 6.
Решение: Найдем сумму всех натуральных чисел от 1 до200:
S200=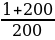 *200 = 20100
*200 = 20100
Найдем сумму всех натуральных чисел, не превосходящих 200, которые делятся на 6: а1=6; d=6; аn=6+6(n-1)=198; 1+n-1=33; n=33.
S33=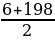 *33=3366; S200-S33=20100- 3366=16734
*33=3366; S200-S33=20100- 3366=16734
Ответ: 16734
Итоговое повторение раздела «Последовательности и прогрессии» направлено на ликвидацию пробелов в знаниях, более глубокому осмыслению основных понятий темы, закреплению умений решать учащимися задач на применение формул n-го члена и суммы первых n членов арифметической и геометрической прогрессий; применять аппарат уравнений и неравенств при решении задач на прогрессии различного уровня сложности. Упражнения для повторения должны как можно полнее охватывать содержание раздела.
4. Фрагмент урока повторения и обобщения изученных методов решения задач на арифметическую прогрессию с использованием ИОР.
III этап
Переходим к следующему этапу работы «Задачи ГИА. 2 часть»
Открываю электронный учебник «Кирилла и Мефодия». Тема: «Арифметическая прогрессия». «Алгоритмы решения задач».
Работа с задачами из электронного учебника.
Задача 1 Дано: а1=3;
n=5;
an=a5=11
Найти: d, S5
Записываем дано, анализируем способ решения задачи.

«Слайд по теме: «Арифметическая прогрессия». Виртуальная школа Кирилла и Мефодия. Алгебра 9»
Слушаем алгоритм авторов учебника.
Решают учащиеся задачи, консультируют в группе. Можно предложить учащемуся оформить на доске.
Запись на доске:
а5=а1+4d
11=3+4d
4d=8
d=2
S5=(a1+a5)*5/2=(3+11)*5/2=35 Ответ d=2; S5=36
Задача 2 Дано: а1=1;
n=6;
S6=36
Найти: d, a6. Записываем дано, анализируем способ решения задачи.
Слушаем алгоритм авторов учебника
Решают самостоятельно. Проверяем ответ. Оценивает группа работу каждого и выставляет в карточку оценку.
Решение:
S6=(a1+a6)*6/2
2*S6=(а1+a6)6
а1+a6=2*36/6
a6=12-а1
a6=11
a6=a1+5d
5d=a6-a1
d=(11-1)/5=2 Ответ: а6=11, d=2
IV этап
Историческая задача. Слушаем задачу, решенную Колмогоровым в 6 лет.
«Слайд. Тема: «Арифметическая прогрессия». Виртуальная школа Кирилла и Мефодия. Алгебра 9»
На доске выписываем задачу:
1+3=22
1+3+5=32
1+3+5+7=42 и т.д. Предлагаю доказать учащимся, используя полученные знания по теме, обсудить в группах, проверяем по тексту слайда.
V этап
Творческие задачи учащихся. Работаем с презентациями учащихся.
А) Задача от будущего медика.
Курс воздушных ванн начинают с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1ч 45 мин?
Решение: (презентация «Задача от медика»)
Имеем арифметическую прогрессию а1=15, d=10, аn=105. Найти n.
Решение:
аn=a1 +(n-1)*d
105=15+(n-1)*10
105=15+10n-10
10n=100
n=10 Ответ: 10 процедур.
Б) Геометрическая задача (презентация «Геометрическая задача»)
Длина сторон прямоугольного треугольника три последовательных члена возрастающей арифметической прогрессии. Найдите разность этой прогрессии, если периметр треугольника равен 120.
Решение.
Пусть разность прогрессии равна d, d0.
Составим систему и решим её
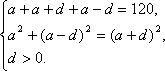
3а=120
а2 -4ad=0
d0
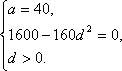
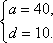
Ответ: d=10.





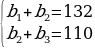
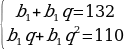
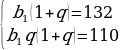
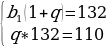
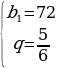
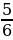 =60, b3 =60*
=60, b3 =60*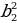 . По условию задачи:
. По условию задачи: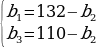
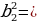 )*(110 – b2)
)*(110 – b2)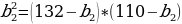 или
или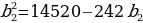 откуда b2 = 60. Тогда b1 = 72, b3 = 50
откуда b2 = 60. Тогда b1 = 72, b3 = 50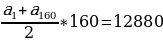 .
.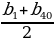 40, S40=
40, S40=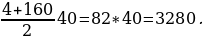
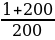 *200 = 20100
*200 = 20100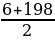 *33=3366; S200-S33=20100- 3366=16734
*33=3366; S200-S33=20100- 3366=16734