Конспект открытого урока по алгебре «Формулы сокращенного умножения», 7 класс
Цели урока:
Образовательные: проверить уровень усвоения учащимися темы, знание ими соответствующих формул и правил.
Развивающие: углубить знания учащихся, развить умения применять приемы сокращенного умножения при решении уравнений, при обнаружении и исправлении ошибок, объяснении своих действий, развитие творческой деятельности учащихся.
Воспитательные: создание условий для включения каждого ученика в активную учебно-познавательную деятельность где каждый может проявить себя, воспитание интереса к математике, расширение кругозора, включение в урок исторического материала.
Тип урока: урок проверки, оценки и коррекции знаний, умений и навыков.
Структура урока:
1) Организационный момент (1 мин)
2) Актуализация знаний (10 мин)
3) Обобщение и систематизация знаний (23 мин)
4) Контроль знаний (7 мин)
5) Домашнего задания (2 мин)
6) Итог урока (2 мин)
Ход урока:
1. Организационный момент.
- Здравствуйте, ребята. Садитесь. На предыдущих уроках вы познакомились с формулами сокращенного умножения. Сегодня мы продолжим эту тему. Вы покажете, как вы знаете эти формулы, как умеете их применять. Запишите в тетрадях число и тему урока.
2. Актуализация знаний:
Ребята, формулы сокращенного умножения имеют широкое применение в математике, особенно в старших классах. Их используют при решении уравнений, раскрытии скобок, разложении многочленов на множители, нахождении значений выражений. Поэтому надо хорошо знать эти формулы и уметь применять их в преобразованиях выражений.
А сейчас мы начнем наш урокс повторения формул и правил. На доске записана левая честь формулы, нужно продолжить формулу, назвать её и рассказать правило.
Оценочный лист.
ФИО------------------------------------------------------------------------------------------
| №1 | №2 | №3 | №4 | №5 Контроль знаний | Всего баллов | Оценка |
|
|
|
|
|
|
|
|
| а2 – в2 = (а – в)(а + в) разность квадратов двух выражений | Разность квадратов двух выражений равна произведению их разности на их сумму. |
| (а + в) 2 = а2 + 2ав + в2
квадрат суммы двух выражений | Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого выражения на второе и плюс квадрат второго выражения. |
| (а – в) 2 = а2 – 2ав + в2
квадрат разности двух выражений | Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого выражения на второе и плюс квадрат второго выражения. |
| (а + в) 3 = а3 + 3а2в + 3ав2 + в3
куб суммы двух выражений | Куб суммы двух выражений равен кубу первого выражения, плюс утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение первого выражения на квадрат второго, плюс куб второго выражения. |
| (а – в) 3 = а3 – 3а2в + 3ав2 – в3 куб разности двух выражений | Куб разности двух выражений равен кубу первого выражения, минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение первого выражения на квадрат второго, минус куб второго выражения. |
| а3 + в3 = (а + в)(а2 – ав + в2)
сумма кубов двух выражений | Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности. |
| а3 – в3 = (а – в)(а2 + ав + в2)
разность кубов двух выражений | Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы. |
1) Работа в парах.
У каждой пары имеется лист с заданием № 1. Установите принцип соответствия и заполните таблицу.
| А)(a+b)2 Б)(a-b)2 В) a2-b2 Г) (a+b)3 Д) (a-b)3
Е) a3+b3 Ж) a3-b3 | 1) (-в-а)(в-а) 2) a3+3a2b+3ab2+b3 3) a3-3a2b+3ab2-b3 4) (a+b)·(a2-ab+b2) 5) (a-b)·(a+b) 6) a2-2ab+b2 7) (b-a)2 8) (a-b)·(a2+ab+b2) 9) (-b+a)2 10) a2+2ab+b2 11) (b+a)2 12) (-a-b)2 |
|
|
|
| А | Б | В | Г | Д | Е | Ж |
| 10,11,12 | 6,7,9 | 1,5 | 2 | 3 | 4 | 8 |
В оценочный лист поставить: если все верные –5баллов, 6 верных – 4 балла, 5 верных – 3 балла, 4 верных -2 балла, меньше 4 верных 0 баллов.
2) Тест – соответствие . Для каждого выражения из левого столбца подберите ему тождественно равное в правом: («5» - все верно, «4» - 1- 2 ошибки, «3» - 3 ошибки)
| № формулы | формула | № ответа | ответ | буква |
| 1 | (x+3)² | 1 | 4x²-9 | О |
| 2 | x²-16 | 2 | 16x²-40xy+25y² | А |
| 3 | (2x-3)(2x+3) | 3 | (x-4)(x+4) | И |
| 4 | 81-18x+x² | 4 | (3y+6x)² | Т |
| 5 | (4x-5y)² | 5 | x²+6x+9 | Д |
| 6 | 25x²-49y² | 6 | (9-x)² | Ф |
| 7 | 9y²+36yx+36x² | 7 | (5x-7y)(5x+7y) | Н |
Каждый ученик получает карточку, выполняет задание, получает соответствия:
1→5(Д), 2→3(И), 3→1(О), 4→6(Ф), 5→2(А), 6→7(Н), 7→4(Т).
Молодцы ребята, вы получили имя великого математика. Показываю его портрет.
Историческая справка: рассказ ученика. (Южиков Алексей). Очень давно, в Древней Греции жили и работали замечательные ученые-математики, которые всю свою жизнь отдали служению науке. В то время, все алгебраические утверждения выражали в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, а произведение двух чисел сравнивали с площадью, трех чисел-с объемом и т.д. первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям был древнегреческий ученый-математик, живший в 3 веке до нашей эры Диофант. Появились формулы, которые стали называться формулами сокращенного умножения.
3) Замените 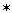 одночленом так, чтобы получившееся равенство было тождеством. (Индивидуальное задание.) Взаимопроверка. («5» - все верно, «4» - 1- 2 ошибки, «3» - 3 ошибки)
одночленом так, чтобы получившееся равенство было тождеством. (Индивидуальное задание.) Взаимопроверка. («5» - все верно, «4» - 1- 2 ошибки, «3» - 3 ошибки)
Ответы:
| 1 | 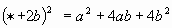
| a |
| 2 | 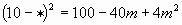
| 2m |
| 3 | 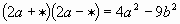
| 3b |
| 4 | 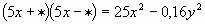
| 0,4y |
| 5 | 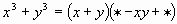
| x2, y2 |
| 6 | 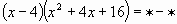
| x3, 64 |
4) Вам нужно найти ошибку в каждой формуле и исправить ее на своих листах.
1. (4у-3х)(4у+3х)=8у²-9у² (вместо 8у² должно быть16у²)
2. 100х²-4у²=(50х-2у)(50х+2у) (вместо50х должно быть10х)
3. (3х+у)²=9х²-6ху+у² (вместо-6ху должно быть+6ху)
4. (6a-9c)²=36a²-54ac+81c² (вместо-54ac должно быть-108ac)
5. х³+8=(х+2)(х²-4х+4) (вместо-4х должно быть-2х)
6. (a-4)(a+4)=a2-4
7. (2x-y)(2x+y)=2x2-y2
8. (x+7)2=x2+49
9. (x+7)2=x2+7x+49
10.(3a-4b)2=9a2-24ab+16b2
В оценочный лист поставить : если верно 9-10 заданий- 5 баллов
7-8 верных -4 балла
5-6 верных – 3 балла
Менее 5 – 2 балла
4. Контроль знаний
Самостоятельная работа
Вариант 1
А1. Представьте трехчлен в виде квадрата двучлена:
а) 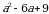 ; б)
; б) 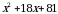 ; в)
; в) 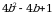 ;
;
г) 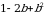 ; д)
; д) 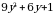 .
.
_________________
А2. Разложите на множители:
а) 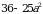 ; б)
; б) 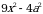 ; в)
; в) 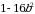 ; г)
; г) 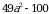 .
.
____________
В1. Преобразуйте в произведение:
а) 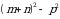 ; б)
; б) 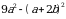 .
.
В2. Найдите значение выражения 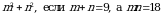 .
.
Вариант 2
А1. Представьте трехчлен в виде квадрата двучлена:
а) 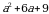 ; б)
; б) 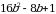 ;
;
А2. Разложите на множители:
а) 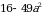 ; б)
; б) 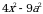 ;
;
____________
В1. Преобразуйте в произведение:
а) 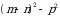 ; б)
; б) 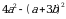 .
.
В2. Найдите значение выражения 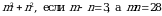 .
.
Если выполнены правильно задания только А1, А2 – оценка «3»
А1, А2, В1или В2- «4», все задания выполнены правильно – «5»
5. Домашнее задание.
Домашняя работа. Применив формулы сокращенного умножения, заполни таблицу: даны 5 пар выражений на «3» 3 любых пары, «4» - 4 пары, «5» заполнена вся таблица. Повторить формулы и правила.
| Выражения | Многочлен равный квадрату суммы этих выражений | Многочлен равный квадрату разности этих выражений | Многочлен равный кубу суммы этих выражений | Многочлен равный кубу разности этих выражений | Разность квадратов этих выражений |
| -5а и b |
|
| | | |
| 3а и 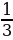 b b | | | | | |
| 5а2 и 0,2b2 | | | | | |
| a2b и –4 | | | | | |
| 6 и х2у2 | | | | | |
6. Итог урока
– Ребята! Наш урок подошел к концу.
Подведем итог:
Каждый ученик сегодня принимал участие в уроке. Сегодня, выполняя разнообразные задания, вы иногда допускали ошибки. И это неудивительно, любой человек не застрахован от ошибок, особенно, когда он только учится овладевать какой-либо наукой. Важно вовремя найти и исправить эти ошибки, понять, почему они появились, и стараться впредь не допускать их.
Давайте, оценим свою активность на уроке и поставим себе оценку за урок: 25-21 баллов – «5», 20-16 баллов - «4», 15-10 баллов - «3».







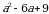 ; б)
; б) 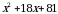 ; в)
; в) 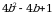 ;
;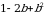 ; д)
; д) 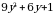 .
.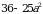 ; б)
; б) 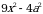 ; в)
; в) 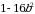 ; г)
; г) 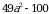 .
.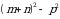 ; б)
; б) 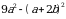 .
. 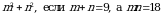 .
.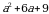 ; б)
; б) 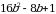 ;
;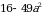 ; б)
; б) 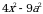 ;
; 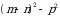 ; б)
; б) 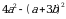 .
. 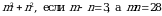 .
.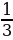 b
b









