Конспект урока по геометрии на тему: «Геометрия без доказательств»

Конспект урока по геометрии на тему: «Геометрия без доказательств»

Цели урока:

1. организовать деятельность учащихся по знакомству с видами фигур (треугольники, прямоугольники, фигуры вращения, пирамиды и т. д.);

Развивающие:

Вызвать интерес у учащихся к предмету;

Воспитательные:

Формирование сознательного использования знаний в практической деятельности;

Оборудование: Компьютер, проектор, интерактивная доска.

Тип урока: комбинированный.

План урока:

• Организационный момент.

• Знакомство с наукой – геометрией.

• Об измерениях.

• Площадь прямоугольного треугольника.

• Дельтоид и параллелограмм.

Ход урока

Витрувий

Геометрия есть знание величин, фигур и их границ, а также отношений между ними и производимых над ними операций, разнообразных положений и движений; она начинает с неделимой точки, завершает объемными фигурами и исследованием многообразных различий между ними, и уже после этого от более сложного возвращается к более простому и к началам более сложного. А именно, она пользуется синтезом и анализом, всякий раз начиная с предпосылок, начала беря от более высокого знания и используя все диалектические методы: когда речь идет о началах, она использует отделение видов от родов и определения; когда о том, что следует за началами, — доказательством и анализом, чтобы показать переход от более простого к более сложному и опять возвращение к более простому, отдельно производя рациональные построения относительно того, что ей подлежит, отдельно — относительно аксиом, от которых она переходит к доказательствам, и относительно постулатов; и отдельно — относительно существенных свойств, показывая, что и они связаны с предметом ее рассмотрения.

I. Организационный момент.

II. Знакомство с наукой – геометрией.

Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида. Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Предложенный Декартом в 1637 году координатный метод лёг в основу аналитической и дифференциальной геометрии, а задачи, связанные с черчением, привели к созданию начертательной и проективной геометрии. При этом все построения оставались в рамках аксиоматического подхода Евклида. Коренные изменения связаны с работами Лобачевского в 1829 году, который отказался от аксиомы параллельности и создал новую неевклидову геометрию, определив таким образом путь дальнейшего развития науки и создания новых теорий.

III. Об измерениях.

С измерением длин и площадей вы уже встречались. Вы помните: чтобы измерить расстояние между двумя точками, нужно узнать, сколько единиц длины содержится между этими точками (рис.1)

Рис.1

А чтобы найти площадь, нужно узнать, сколько единиц площади помещается в этой фигуре (рис.2)

единица площади

Рис.2

Современные меры длины появились во Франции около 200 лет тому назад. Это миллиметр (мм), сантиметр (см), метр (м), дециметр (дм), километр (км). От этих единиц произошли меры площади: квадратный миллиметр ( мм²), квадратный сантиметр (см²), квадратный метр ( м²), квадратный дециметр (дм²), квадратный километр (км²).

До сих пор иногда пользуются старинными мерами. Например, дюйм –старинная английская мера (приблизительно 2,5см).

Единица площади –это площадь квадрата, сторона которого равна единице длины. Например, квадратный метр –это площадь квадрата со стороной 1 м.

Задание 1.

На рисунках 3 и 4 изображены квадраты площадью в один квадратный сантиметр и в один квадратный дециметр. Узнай, сколько квадратных сантиметров в одном квадратном дециметре.

Рис.4

Квадратный дециметр

Что такое куб, ты знал еще до школы, Поверхность куба состоит из шести одинаковых квадратов, которые называются гранями.

Стороны этих квадратов называются ребрами куба. Все ребра куба равны между собой (Рис.5).

Рис.5

Задание 2.

Сосчитай, сколько ребер у куба.

Задание 3.

Одно из ребер куба равно 5 см. Найди сумму длин всех ребер.

Задание 4.

Сколько кубических сантиметров содержится в каждой фигуре? (Рис.6)

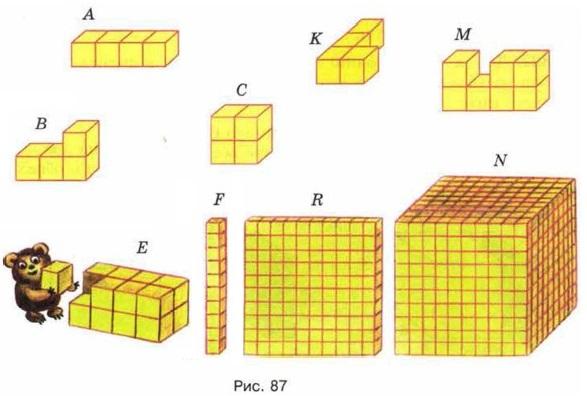
1 кубический сантиметр

Рис.6

Литр

Количество вещества можно измерять по-разному. Иногда определяют массу вещества, иногда - его объем.

Литр – это кубический дециметр. Упаковку для 1 литра молока можно склеить в форме куба, используя следующие развертки: ( Рис.7)

Рис.7

IV. Площадь прямоугольного треугольника

Задание 1.

Вычисли площадь прямоугольника и площадь квадрата, изображенных на рисунке 8.

Для решения этой задачи формула S= ab, где a и b стороны прямоугольника.

Площадь треугольника легко найти, если этот треугольник является половиной прямоугольника. Тогда мы находим площадь этого прямоугольника и делим его пополам.(Рис.9)

Рис.9

Дельтоид и параллелограмм.

Дельтоид — четырёхугольник, обладающий двумя парами сторон одинаковой длины. В отличие от параллелограмма, равными являются не противоположные, а две пары смежных сторон. Выпуклый дельтоид имеет форму, похожую на воздушного змея. (Рис.10)

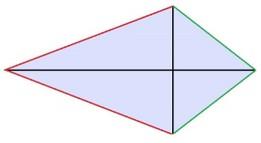
Рис.10

Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны. (Рис.11)

Рис.11

Рис.12

Задание 1.

Найти площадь параллелограмма, изображенного на рисунке 12.

Рис.13

Задание 2.

Перерисуй и вырежь 2 треугольника, равных треугольнику на рисунке 13.Наклей их на лист бумаги так, чтобы получился дельтоид.

Задание3.

Перерисуй и вырежь 2 треугольника, равных треугольнику на рисунке 13.Наклей их на лист бумаги так, чтобы получился параллелограмм.