Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.
Конец отрезка, лежащий в плоскости, называется
основанием наклонной.

AB - наклонная.
B - основание наклонной.
Перпендикуляром, проведенным из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости.
Конец этого отрезка, лежащий в плоскости, называется
основанием перпендикуляра.

AC - перпендикуляр.
C - основание перпендикуляра.
Расстоянием от точки до плоскости называется
длина перпендикуляра, проведенного из этой точки к плоскости.
Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется
проекцией наклонной.

CB - проекция наклонной AB на плоскость α.
Треугольник ABC прямоугольный.
Углом между наклонной и плоскостью называется угол между этой наклонной и её проекцией на плоскость.

∢CBA - угол между наклонной AB и плоскостью α.

Если AD>AB, то DC>BC
Если из данной точки к данной плоскости провести несколько наклонных, то большей наклонной соответствует большая проекция.
∢DAB - угол между наклонными
∢DCB - угол между проекциями
Отрезок DB - расстояние между основаниями наклонных.

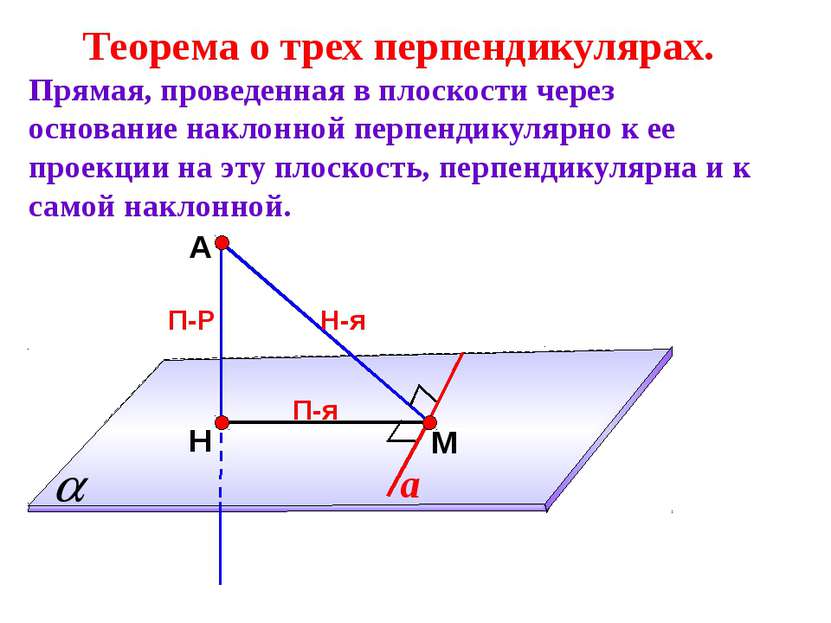
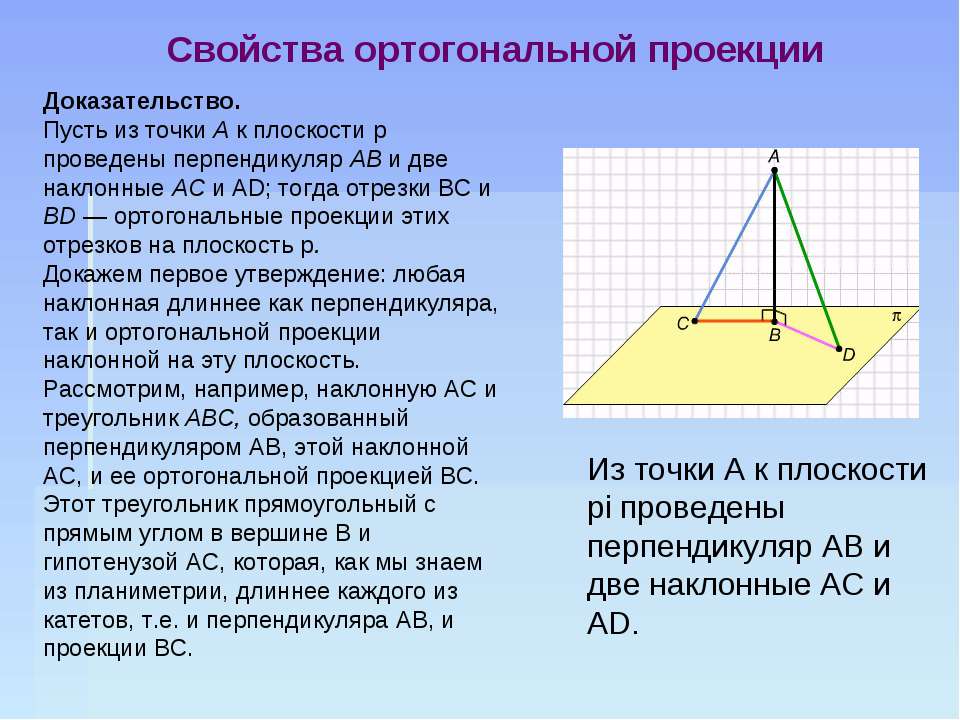







 AB - наклонная.
B - основание наклонной.
AB - наклонная.
B - основание наклонной.
 AC - перпендикуляр.
C - основание перпендикуляра.
Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к плоскости.
Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
AC - перпендикуляр.
C - основание перпендикуляра.
Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к плоскости.
Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
 CB - проекция наклонной AB на плоскость α.
Треугольник ABC прямоугольный.
Углом между наклонной и плоскостью называется угол между этой наклонной и её проекцией на плоскость.
CB - проекция наклонной AB на плоскость α.
Треугольник ABC прямоугольный.
Углом между наклонной и плоскостью называется угол между этой наклонной и её проекцией на плоскость.
 ∢CBA - угол между наклонной AB и плоскостью α.
∢CBA - угол между наклонной AB и плоскостью α.
 Если AD>AB, то DC>BC
Если из данной точки к данной плоскости провести несколько наклонных, то большей наклонной соответствует большая проекция.
∢DAB - угол между наклонными
∢DCB - угол между проекциями
Отрезок DB - расстояние между основаниями наклонных.
Если AD>AB, то DC>BC
Если из данной точки к данной плоскости провести несколько наклонных, то большей наклонной соответствует большая проекция.
∢DAB - угол между наклонными
∢DCB - угол между проекциями
Отрезок DB - расстояние между основаниями наклонных.













