Метод границ или метод оценки

Разработка урока по математике (алгебра 10 класс).

Тема: «Решение уравнений методом оценки (методом границ)».

Цели урока:

-образовательные:

• привести в систему знания учащихся по теме «Тригонометрические уравнения»,

• научить решать уравнения методом оценки, т.е. углубить знания учащихся по теме.

-развивающие:

• развитие умений учащихся сравнивать, анализировать и применять в изменённой ситуации полученные знания.

-воспитательные:

• воспитание потребности в знаниях,

• выработка желания глубины проникновения в предмет.

-методическая цель урока:

• реализация вариативной части учебного плана.

Тип урока: изучение нового материала.

Ход урока:

1. Мотивация учебной деятельности (эпиграф урока (приложение 1, 1 слайд), постановка перед учащимися целей урока, сообщение плана урока).

1. Актуализация опорных знаний:

а) устная работа

1. Назвать типы тригонометрических уравнений и методы их решения (приложение 1, 2 слайд)

предполагаемые ответы:

2. составить алгоритм решения следующих уравнений (приложение 1, 3 слайд)

1. Изучение нового материала.

Изучение нового материала начинается с проблемной ситуации – решить уравнения

(приложение 1, 4 слайд):

1. cos x = 1+ x²

(это уравнение решено графически в учебнике А.Г. Мордковича для 10-11 кл., 2007г.[6], § 10, стр.52, пример 1) (Рисунок 1)

Решение этого уравнения методом оценки не вызывает трудностей у учащихся:

Е(cos x)=[-1; 1], Е(1+ x²)= [1; +∞], значит равенство (cos x = 1+ x²) выполняется, если 1+ x² =1 и cos x=1. Решая уравнение, 1+ x² =1, получаем корень х=0 (cos 0=1).

Ответ: х=0.

2. sin 2x + cos x = 2

-1 ≤ sin 2x ≤ 1, -1 ≤ cos x ≤ 1. Делаем вывод, что cos x =1 и sin 2x =1. Решая уравнение cos x =1, получаем х= 2πк, кZ. Для уравнения sin 2x =1 (sin(2∙2πк)≠1) х= 2πк не является решением.

Ответ: нет решений.

3. sin(π∙cos 2x) = 1

π∙cos 2x=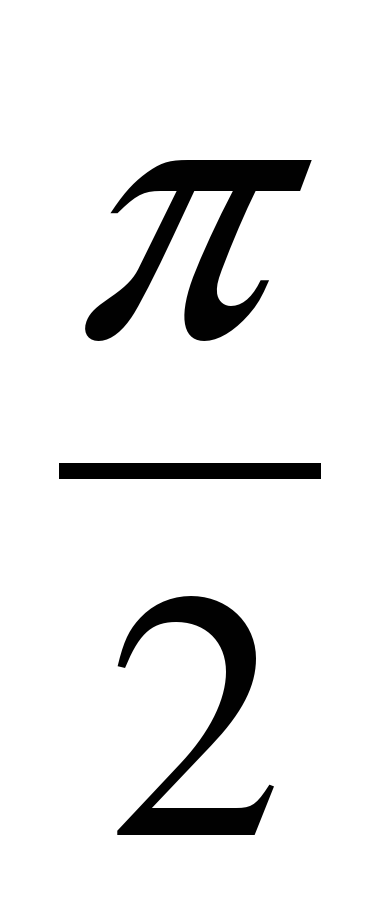+2πк, кZ

cos 2x=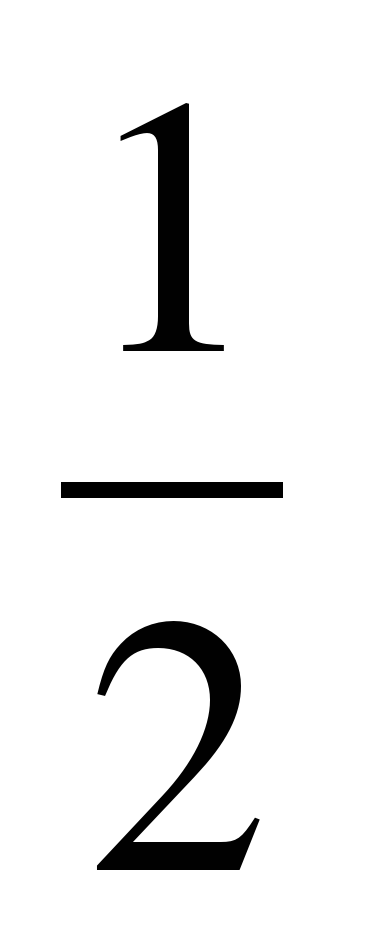+2к, учитывая, что -1 ≤ cos 2 x ≤ 1, получаем неравенство -1 ≤ 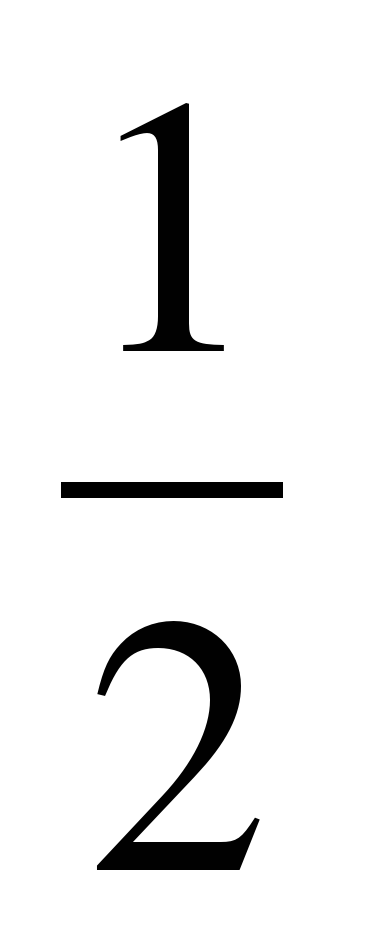+2к ≤ 1, -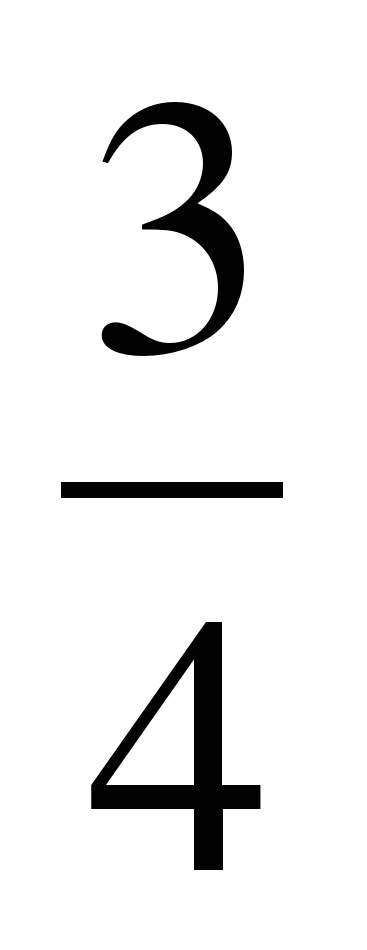≤ к ≤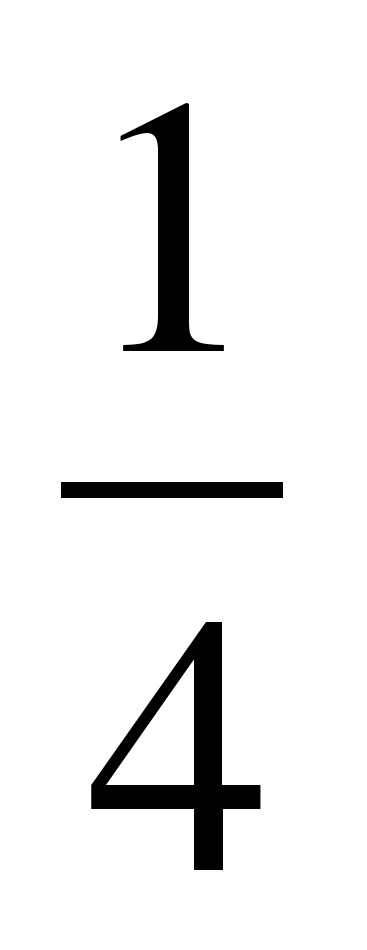, т.к. кZ, отсюда следует, что к=0.

cos 2х =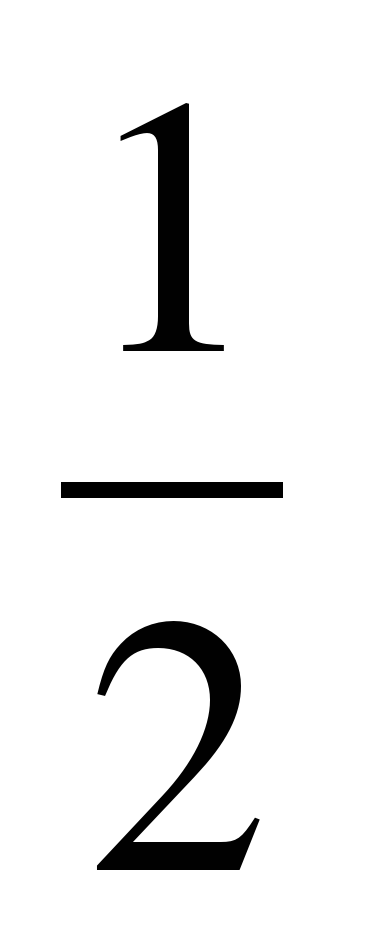+2∙0, cos 2х =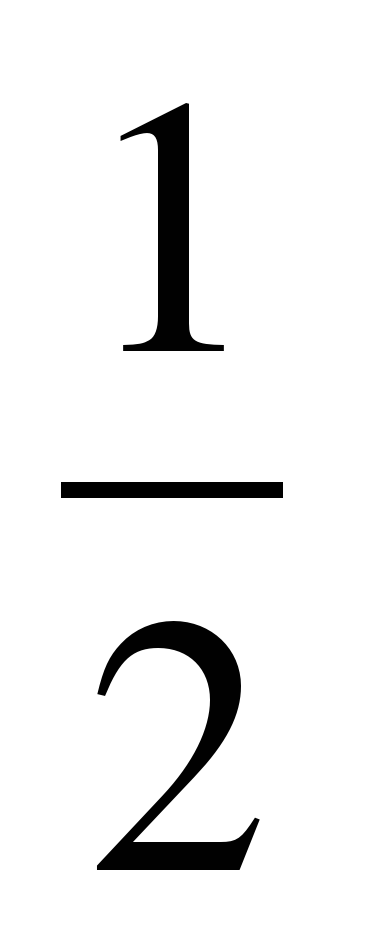, х= ± 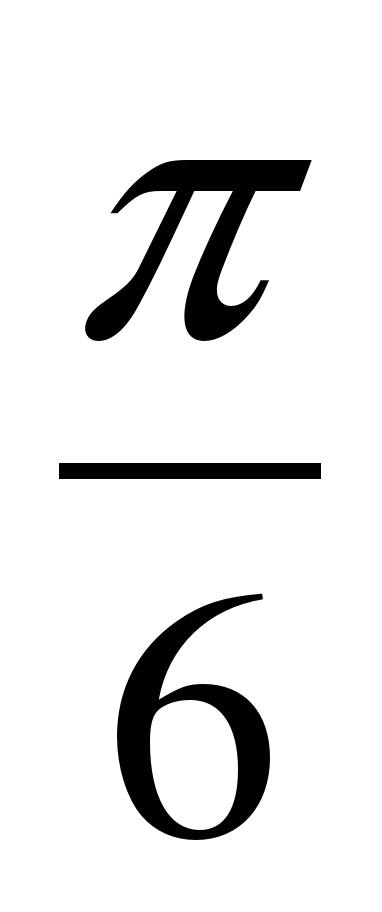+ πп, п Z

1. Отработка первоначальных навыков решения уравнений методом оценки.

Каждому ученику предлагается карточка с набором уравнений и даётся на обдумывание способа решения 5-7 мин, затем необходимо обсудить подходы к решению уравнений. Если в этом есть необходимость, уравнения, вызвавшие затруднения разбираются у доски, но целесообразно дать детям самостоятельно попытаться решить данные уравнения.

Подобрать уравнения можно из различной литературы, в зависимости от подготовленности детей.

Я предлагаю следующие уравнения:

1. cos x = 1+ sin² x

1. cos⁶ х + sin² 3х + 4 sin 9х = 7

1. – cos (7 πх) =х²-6х+10

1. tg (π sin х) = -

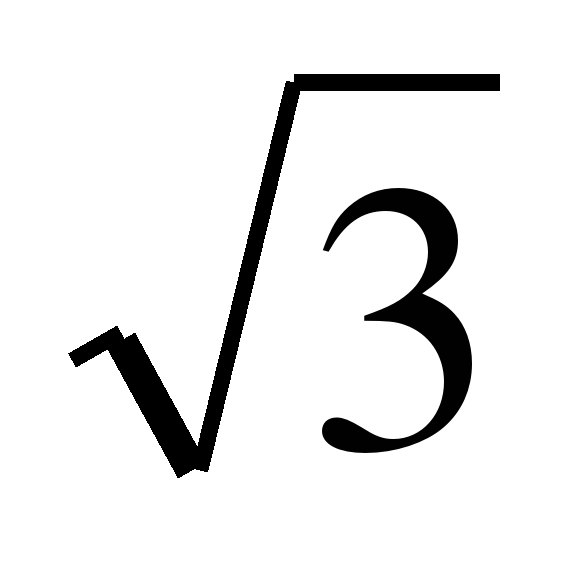
2. sin х + sin 5х=2

3. (cos 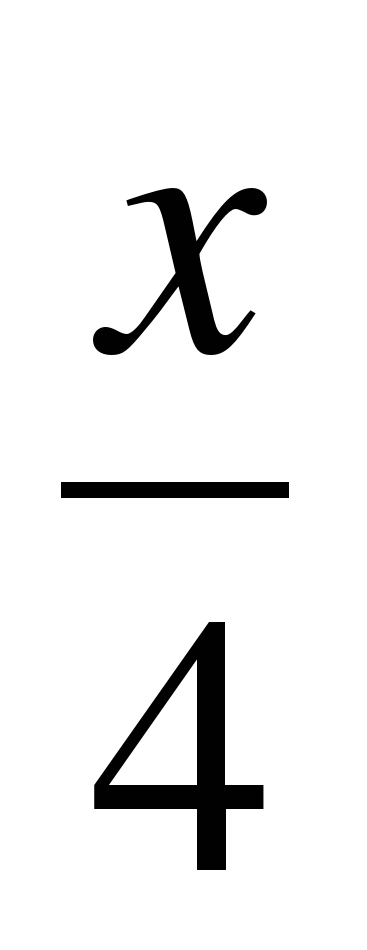 - 2 sin х) sin х + ( 1+ sin  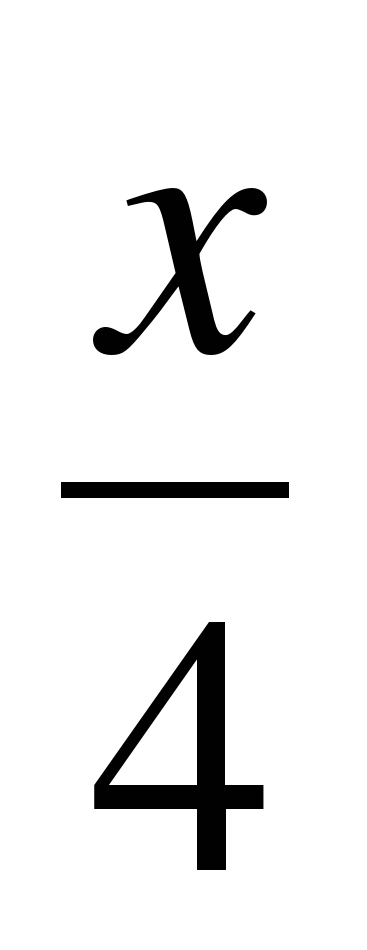- 2 cos x ) cos x = 0

V. Домашнее задание.

А.Г. Мордкович «Алгебра и начала анализа, 10-11 кл. Задачник, 2007 г.» [5]

№ 183(а,б), 186(в), 209(а,в,г)- решить методом оценки.

VI. Подведение итогов урока.

Литература:

1. «Математика в школе» № 3-1999 г. статья А.А. Аксёнова «Решение задач методом оценки».

2. М.И. Сканави «Сборник задач по математике для поступающих в ВУЗы», Москва «ОНИКС 21 век», «Мир и Образование», 2002.

3. В. М. Говоров, П.Т. Дыбов, Н.В. Мирошин, С.Ф. Смирнова «Сборник конкурсных задач по математике для поступающих в ВУЗы», Москва «ОНИКС 21 век», «Мир и Образование», 2003.

4. КИМы ЕГЭ 2006 г.

5. А.Г. Мордкович «Алгебра и начала анализа, 10-11 кл. Задачник, 2007 г.»

6. А.Г. Мордковича «Алгебра и начала анализа, 10-11 кл. Учебник, 2007 г.»

Рис. 1

Тригонометрические уравнения

Уравнение представляет собой наиболее серьёзную и важную вещь в математике.

О.Лодж

Задание . Составьте алгоритм решения уравнений.

• 2 cos x+1 = 0
• sin x+2 = 0
• sin x+0 , 5 = 0
• 2 sin x-2 = 0
• 3cos 2 x-10cos x +3 = 0
• cos 2 x – 2 cos x = 0
• sin 2 x – 16 = 0
• cos 3x + sin 3x = 0
• 6sin 2 x – sin x cos x- cos 2 x = 3
• sin 2x + cos x = 2

Решение уравнений с использованием ограниченности функций y = cos x и y = sin x

• cos x = 1+ x 2 sin 2x + cos x = 2 sin( π∙ cos 2x) = 1
• cos x = 1+ x 2 sin 2x + cos x = 2 sin( π∙ cos 2x) = 1
• cos x = 1+ x 2 sin 2x + cos x = 2 sin( π∙ cos 2x) = 1
• cos x = 1+ x 2 sin 2x + cos x = 2 sin( π∙ cos 2x) = 1
• cos x = 1+ x 2
• sin 2x + cos x = 2
• sin( π∙ cos 2x) = 1