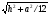Просмотр содержимого документа
«Многогранники. ПИРАМИДА»
Инструкционная карта № 28
Тақырыбы/ Тема: Решение задач по теме: «Пирамида».
Мақсаты/ Цель:
1.Познакомить учащихся с понятием пирамиды, ее элементов, видов пирамиды, построение сечений в пирамиде, определение площади поверхности пирамиды, усеченной пирамиды.
2.Создать атмосферу коллективного поиска, эмоциональной приподнятости, радости познания трудностей.
3.Создать условия для формирования умений сравнивать, классифицировать изучаемые факты и понятия.
Теоретический материал:
| Правильная пирамида |
| 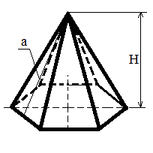
| Sбок = ½ Pосн a; где а-апофема a; где а-апофема Sпир = Sосн. + Sбок.
V = (Sосн H) / 3 |
| Правильная усеченная пирамида |
| 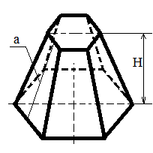
| Sбок = ½ (Pосн1 + Pосн2) a; где a; где а – апофема Sус.пир.= Sосн.1+ Sосн.2+ Sбок.
V = H (Sосн1 + Sосн2 + √(Sосн1 Sосн2)) / 3 |
Решение задач:
Стороны оснований правильной усеченной пирамиды 4 дм и 1 дм. Боковое ребро 2 дм. Найдите высоту пирамиды.
Дано: АВСА1В1С1 – усеченная
А1
В1
О1
пирамида, АВ=ВС=СА=4 дм,
C1
А1В1=В1С1=С1А1=1 дм,
АА1=ВВ1=СС1=2 дм.
В
А
В2
О
Найти: Н
Решение:
С
R=О1В1=А1В1/ =1/
=1/ =
= /3 r=ОВ=АВ/
/3 r=ОВ=АВ/ =4/
=4/ =4
=4 /3
/3
В1В2=ОО1=Н из  ВВ1В2
ВВ1В2  В2=900 ВВ2=4
В2=900 ВВ2=4 /3-
/3- /3=3
/3=3 /3=
/3=
Н=В1В2= (дм)
(дм)
По стороне основания, а высоте h найдите полную поверхность правильной
пирамиды: 1) треугольной; 2) четырехугольной; 3) шестиугольной.
Дано: SАВС – пирамида, SO=h,
АВ=ВС=АС=а.
А
Найти: Sпол
О
В
Решение:
К
C
Sпол=Sосн+Sбок Sосн =а2 /4 OK=r r=а3/2
/4 OK=r r=а3/2 = а/2
= а/2
Рассм.  SОК SК=
SОК SК=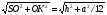 Sбок =1/2*3а*
Sбок =1/2*3а*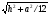
Sпол =а2  /4+3а/2*
/4+3а/2*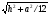 =а
=а /4(а +
/4(а +  )
)
S

Дано: SАВС Д – пирамида,
АВ=ВС=ДС=АД=а. SO=h,
C
В
О
К
Найти: Sпол
D
А
Решение:
Sпол=Sосн+Sбок Sосн=а2 OK=r r=а4/2=а/2
Рассм. 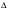 SОК SК=
SОК SК= Sбок =1/2*4а*
Sбок =1/2*4а* 
Sпол =а2 +1/2*4а*  =а (а+
=а (а+ )
)
S
Дано: SАВС Д ЕF – пирамида, SO=h,
АВ=ВС=ДС=EД=EF=FA=а.
C
В

D
О
А
Найти: Sпол
Е
F
К
Решение:
Sпол=Sосн+Sбок Sосн=3a2  /2 OK=r r=3а6/2
/2 OK=r r=3а6/2 =3а/2
=3а/2
Рассм. 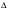 SОК SК=
SОК SК= Sбок =1/2*6а*
Sбок =1/2*6а* 
Sпол =3а2  /2+ 3а
/2+ 3а =3а/2(а
=3а/2(а +
+ )
)
Основание пирамиды – прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см. Вычислите высоту пирамиды.
Дано: SАВСD – пирамида, АD=ВС=6 см,
АВ=DС=8 см, SА=SВ=SС=SD=13
см
В
C
Найти: SO
о
А
Решение:
D
Рассм. 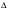 АDС АС=ВD=
АDС АС=ВD= =
= =
= (см)
(см)
DО=ОВ=АО=ОС=1/2АС=1/2ВD=5 (см)
Рассм. 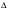 DSO SO=
DSO SO=  (cм)
(cм)
Практическая часть:
1 вариант
В правильной треугольной пирамиде через середину боковых ребер проведено сечение. Найдите ее площадь, если длина ребра основания пирамиды равна 24 см.
Боковые ребра пирамиды равны гипотенузе прямоугольного треугольника, лежащего в ее основании. Найдите высоту пирамиды, если ее боковое ребро равно 2 см.
Стороны оснований правильной треугольной усеченной пирамиды 4 дм и 1 дм. Боковое ребро 2 дм. Найдите высоту пирамиды.
Стороны основания правильной треугольной пирамиды а, боковое ребро в. Определите высоту пирамиды.
2 вариант
Высота правильной четырехугольной пирамиды 7, а сторона основания 8. Найти боковое ребро.
Найти полную поверхность правильной четырехугольной пирамиды, если высота ее равна 2 м, а сторона основания 4,2.
В правильной четырехугольной пирамиде все ребра равны 1 м. Найдите высоту пирамиды.
Апофема правильной усеченной четырехугольной пирамиды равна 6 см, а сумма всех ребер оснований равна 32 см. Вычислите площадь боковой поверхности пирамиды.
3 вариант
По данной стороне основания а=9 и боковому ребру в=6. Найти высоту правильной пирамиды.
Найдите площадь диагонального сечения правильной четырехугольной пирамиды, если сторона ее основания равна 1, а боковое ребро .
.
Каждое ребро четырехугольной пирамиды равно 3 м. Вычислите площадь полной поверхности пирамиды.
Апофема правильной усеченной треугольной пирамиды равна 8 cм, а сумма всех ребер оснований равна 24 см. Вычислите площадь боковой поверхности пирамиды.
4 вариант
Найдите площадь поверхности правильного тетраэдра с ребром равным а=2.
Основанием пирамиды служит прямоугольник со сторонами 6 и 15. Высота пирамиды, равная 4, проходит через точку пересечения диагоналей основания. Найдите площадь боковой поверхности пирамиды.
Плоский угол при вершине правильной шестиугольной пирамиде равен 300. Боковое ребро  =2. Найдите боковую поверхность пирамиды.
=2. Найдите боковую поверхность пирамиды.
В правильной четырехугольной усеченной пирамиде стороны оснований 8 м и 2 м. Высота равна 4 м. Найдите полную поверхность усеченной пирамиды.
Контрольные вопросы:
Какие виды вы знаете пирамид?
Назовите свойства правильной пирамиды. Как можно получить из пирамиды усеченную пирамиду?
Могут ли быть равными апофема и высота у правильной пирамиды?
Сколько граней, вершин, ребер у семиугольной пирамиды?
2. Какое наименьшее число граней, ребер, вершин может иметь пирамида?
3. Сколько граней, ребер, вершин имеет пятиугольная усеченная пирамида?
4. Существует ли усеченная пирамида, все ребра которой равны?
5. Основание пирамиды – четырехугольник, все стороны которого равны. Высота пирамиды проходит через точку пересечения диагоналей основания. Является ли данная пирамида правильной?
6. Докажите, что треугольная пирамида, все грани которой – равносторонние треугольники, является правильной.








 a; где а-апофема
a; где а-апофема

 =1/
=1/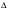 ВВ1В2
ВВ1В2 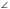 В2=900 ВВ2=4
В2=900 ВВ2=4 (дм)
(дм)
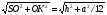 Sбок =1/2*3а*
Sбок =1/2*3а*