Необычные кольца Мебиуса

Необычные кольца Мебиуса

Выполнили:

Поправка Алёна ,

Коновалова Елизавета

ученицы 7 «б» класса

Школа 168

Руководитель проекта Чистякова Т.В.

Новосибирск 2018

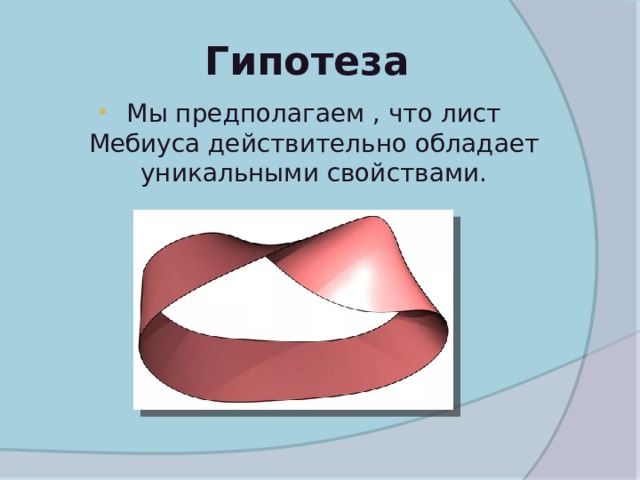
Гипотеза

• Мы предполагаем , что лист Мебиуса действительно обладает уникальными свойствами.

Цель:

Убедиться в том, что лента Мебиуса нашла применение во многих привычных для нас сферах жизни

Задачи :

1)Выяснить свойства листа Мебиуса;

2)Познакомиться с биографией Мебиуса и с историей его замечательного открытия

3)Показать необычность этой геометрической поверхности на практике

Открытие Августа Мебиуса

• «Отцом» открывателем этой необычной ленты признан немецкий математик Август Фердинанд Мебиус, ученик Гаусса, написавший не одну работу по геометрии, но прославившийся преимущественно открытием односторонней поверхности в 1858 году. 

• Удивительным является тот факт, что ленту с одной поверхностью в тот же самый 1858 год открыл другой ученик Гаусса – талантливый математик Иоганн Листинг, придумавший термин «топология» и написавший серию основополагающих трудов по этому разделу математики.

Лента Мебиуса - удивительное открытие

Практически все знают, как выглядит символ бесконечности, напоминающий перевернутую восьмерку. Этот знак называют еще «лемниската», что с древнегреческого означает лента .

Что такое Лента Мебиуса?

• Лента Мебиуса (или ее еще называют петля Мебиуса, лист Мебиуса и даже кольцо Мебиуса) – одна из наиболее известных в математике поверхностей. Петля Мебиуса - это петля с одной поверхностью и одним краем.

«Магия» ленты Мебиуса

• Несмотря на кажущееся наличие у листа Мебиуса двух сторон, на самом деле сторона всего одна, и раскрасить в два цвета ленту не получится.
• Если ручкой или карандашом начертить по всей длине петли линию, не отрывая руку от листа, то грифель в конечном итоге остановится в точке, с которой Вы начали чертить линию;
• Примечательные опыты получаются при разрезании ленты, способные удивить, как взрослого, так и ребенка в особенности.

Практическая работа:

Вопрос

Гипотеза

Что будет, если ленту разрезать вдоль по середине?

Эксперимент

Получим 2 отдельных листа Мебиуса

Что будет, если ленту разрезать 2 раза вдоль по середине?

Получим одно кольцо , увеличенное в 2 раза

Следуя из опыты №1 получим кольцо в 4 раза больше начального

Получим 2 одинаковых по величине кольца , скрепленных друг с другом.

Использование ленты Мебиуса в наше время

• Лента Мебиуса – вовсе не абстрактная фигура, нужная лишь для целей математики, она нашла применение и в реальной повседневной жизни. По принципу этой ленты функционирует в аэропорту лента, передвигающая чемоданы из багажного отделения. Такая конструкция позволяет ей служить дольше в связи с равномерным изнашиванием. Открытие Августа Мебиуса повсеместно используется в станкостроении. Конструкцию используют для большего времени записи на пленку, а также в принтерах, использующих ленту при распечатке.

Лента Мебиуса – широкое поле для Вдохновения

• Самой известной работой, посвященной ленте Мебиуса считается картина Moebius Strip II, Red Ants или Красные Муравьи голландского художника-графика Маурица Эшера. На картине представлены муравьи, карабкающиеся по петле Мебиуса с обеих сторон, на самом деле сторона всего одна. Муравьи ползут по бесконечной петле друг за другом по одной и той же поверхности.

• Художник черпал свои идеи из статей и трудов по математике, он был глубоко увлечен геометрией. В связи с чем на его литографиях и гравюрах часто присутствуют различные геометрические формы, фракталы, потрясающие оптические иллюзии.
• До сих пор интерес к петле Мебиуса находится на очень высоком уровне, даже спортсмены ввели одноименную фигуру высшего лыжного пилотажа.

• В форме петли Мебиуса создается огромное множество украшений, обуви, скульптур и многих других предметов и форм .

• Лист Мебиуса наложил отпечаток на производство, дизайн, искусство, науку, литературу, архитектуру.

Вывод

• Прочитав определённую литературу, мы познакомились с геометрической поверхностью лентой Мебиуса; анализируя собранный материал, мы увидели необычность этой ленты; провели опыты с листом и доказали, что он изменяет свои свойства при разрезании; мы считаем правильным, что лист Мебиуса считают символом современной математики, так как именно он дал толчок новым математическим исследованиям, наша гипотеза подтвердилась.

Список литературы

• М. В. Величко «Математика 9-10 классы. Проектная деятельность учащихся»: Волгоград:

• «Математика «Большой справочник для школьников поступающих в вузы»»: М.: «Дрофа», 2002. – С. 864 «Энциклопедия для детей «МАТЕМАТИКА»» том 11, М.: Аванта +; 2002. С. 687.

Материалы сайтов:

• http://arbuz.uz/t_lenta
• https://econet.ru