Общие изменения в преподавании математики с внедрением ФГОС

Общие изменения в преподавании математики, связанные с внедрением ФГОС

Личность в современном информационном обществе. Результаты исследований математической подготовки современных российских школьников. Предпосылки разработки ФГОС второго поколения. Политика в области математического образования. Требования ФГОС. Структура учебной деятельности. Системно-деятельностный подход. Заключение.

Лекция.

Личность в современном информационном обществе

В последние десятилетия, при переходе к постиндустриальному обществу, логика развития производственной сферы привела к осознанию того, что истинное совершенствование жизни связано не столько с внешней образованностью человека, усвоением им той или иной системы знаний и умений, сколько с развитием его ума и способностей, системы ценностей и мотивационных установок. Сегодня - это не просто вопрос успешности человека в жизни, что, естественно, очень важно. Но это еще и вопрос безопасности и конкурентоспособности страны, условие ее расцвета и мирного развития.

Современная жизнь предъявляет к человеку новые требования. Общество нуждается в людях творчески мыслящих, любознательных, активных, умеющих принимать нестандартные решения и брать ответственность за их принятия, а также умеющих осуществлять жизненный выбор.

Личность в современном информационном обществе понимается как субъект, реализующий свой интеллектуальный потенциал в социуме, информационно-образовательной среде, взаимодействуя с информационными ресурсами, используя современные информационно-коммуникативные технологии. Это предполагает, в частности, высокий уровень «информационного сознания» при широком доступе к информации, противодействие негативной информации, что посильно только интеллектуально развитому человеку.

Результаты исследований математической подготовки современных российских школьников

В интеллектуальное становление личности неоценимый вклад вносят специфические черты математики как науки и как учебного предмета. Математика занимает особое место в науке, культуре и общественной жизни, являясь одной из важнейших составляющих мирового научно-технического прогресса.

Каково же состояние математической подготовки современных российских школьников? Приведём краткие результаты международных мониторинговых исследований качества математического образования школьников TIMSS (Trends in Mathematics and Science Study) и PISA (Programme for International Student Assesment).

В проводимом 1 раз в 4 года исследовании TIMSS, организатор которого – Международная ассоциация по оценке образовательных достижений, участвуют российские школьники 4-х и 8-х классов, при этом проверяются достижения учащихся начальной и основной школы. По качеству математического и естественнонаучного образования российские школьники находятся в первой десятке из более четырёх десятков стран мира. В то же время невысоки результаты при выполнении заданий, составленных на материале курса математики 5–6 классов российской школы. Российские восьмиклассники не умеют эффективно применять полученные знания при выполнении нестандартных заданий по алгебре, связанных с выявлением закономерностей, разрешением проблем, возникающих в реальной ситуации, описанной в условии задачи. Это связано с тем, что обучение решению задач фактически завершается в 5–6 классах, а в курсе алгебры не поддерживается систематическим повторением и учащимся не предлагаются задачи практического содержания.

Совсем иные результаты показывает проводимое один раз в три года исследование PISA, которое осуществляется ОЭСР — Организацией экономического сотрудничества и развития. Это исследование направлено на оценку способности учащихся применять полученные в школе математические знания и умения в жизненных ситуациях. В нём принимают участие до 10000 школьников 12–15 лет из 65 стран–членов ОЭСР. По результатам этого исследования Россия стабильно получает баллы ниже среднего. Исследование PISA оценивает:

• во-первых, математическую грамотность – способность человека определять и понимать роль математики в мире, в котором он живёт, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину;

• во-вторых, читательскую грамотность (в том числе чтение математических текстов) – способность человека понимать и использовать письменные тексты, размышлять о них и заниматься чтением для того, чтобы достигать определённых целей, расширять свои знания и возможности, участвовать в социальной жизни.

Исследование показало, что в российской школе существуют значительные проблемы в формировании читательской грамотности. Следовательно, необходимо найти более разнообразные пути обучения учащихся работе с текстами различного содержания, характера и формата при освоении каждой учебной дисциплины.

Учебная информация школьного курса математики должна быть представлена в различных формах и использоваться не только в качестве иллюстраций, но и в виде учебных задач, решение которых предполагает самостоятельную интерпретацию текстов, выдвижение гипотез о его содержании, рефлексию, оценку и др.

• в-третьих, компетентность в решении проблем – способность использовать познавательные умения для решения межпредметных реальных проблем. Для успешного решения предлагаемых проблем выделены следующие познавательные общеучебные умения:

1. понимать проблему;

2. характеризовать проблему;

3. представлять проблему;

4. решать проблему;

5. размышлять над её решением;

6. сообщать решение проблемы.

Применение этих умений требует от учащегося владения навыками аналитических рассуждений.

Отмечается, что невысокие результаты российских учащихся в области решения проблем по сравнению с их сверстниками из большинства ведущих стран, участвовавших в исследовании, связаны с тем, что школьное образование России ориентировано, в основном, на формирование у учащихся предметных знаний и умений.

Впрочем, следует отметить тенденцию некоторого улучшения показателей за последние годы, и это свидетельствует о том, что меры, принимаемые Минобрнауки России, дают положительные результаты.

Предпосылки разработки ФГОС второго поколения

Результаты исследования TIMSS и PISA вызвали широкую дискуссию в научных общественных кругах о конкурентоспособности российского, в частности, математического образования. Появилась настоятельная необходимость модернизации российского образования, направленная на повышение его качества, на его совершенствование при условии сохранения достигнутого интеллектуального потенциала.

Учёные отмечают, что математическая компетентность в разных формах должна быть развита у всех категорий населения. Ряд принципиальных вопросов, относящихся к развитию математического образования, не может быть решен внутри него и требует обращения к общей проблематике системы образования и развития России.

Ещё в 1997 г. был разработан российский проект федерального компонента стандартов, который не был утверждён законодательно. Вместо него в 1998 году был принят «Обязательный минимум содержания начального, основного, среднего (полного) общего образования». На основе этого документа, который стал считаться стандартом, были разработаны примерные программы по математике.

В 2002– 2003 гг. коллективом учёных под руководством Э. Д. Днепрова был разработан и утверждён Минобрнауки России Федеральный компонент государственных образовательных стандартов начального, основного и среднего (полного) общего образования. В нём впервые закреплялась вариативность, дифференциация и индивидуализация обучения – вводилось профильное обучение, предусматривалось существенное обновление содержания образования, большее значение отводилось прикладной направленности образования и его практической значимости.

Несмотря на перечисленные положительные моменты, руководитель проекта Э. Д. Днепров отмечал, что коллективу разработчиков так и не удалось преодолеть предметно-академическую традицию в определении содержания образования. Этот стандарт был «переходным» и выполнил свою положительную подготовительную функцию в деле дальнейшего совершенствования школьного образования, связанного с актуализацией системно-деятельностного подхода, а также способствовал появлению новых направлений исследований, в частности, компетентностного подхода в образовании.

Политика в области математического образования

В настоящее время основные принципы государственной политики РФ в сфере образования, общие правила функционирования системы образования и осуществления образовательной деятельности устанавливает новый Федеральный закон «Об образовании в Российской Федерации»¹.

Сегодня стратегическая цель российского образования – воспитание успешного поколения граждан страны, владеющих современными знаниями, навыками и компетенциями, на идеалах демократии и правового государства в соответствии с национальными и общечеловеческими ценностными установками.

Именно в школе – единственном социальном институте, через который проходят все граждане России, должна быть сосредоточена не только интеллектуальная, но и гражданская, духовная, культурная жизнь подростка.

Необходимым условием организации и функционирования такой школы является реализация Федерального государственного образовательного стандарта основного и полного (среднего) общего образования.

Отличительной особенностью нового стандарта является его деятельностный характер, ставящий главной целью развитие личности учащегося. Система образования отказывается от традиционного представления результатов обучения в виде знаний, умений и навыков.

Формулировки стандарта указывают реальные виды деятельности, которыми учащийся должен овладеть к концу обучения. Требования к результатам обучения сформулированы в виде личностных, метапредметных и предметных результатов.

Образовательная политика в области общего математического образования должна опираться не только на Стандарты, но и на профессиональный стандарт педагога, включающий модуль «Предметное обучение. Математика» (2013), а также на Концепцию развития математического образования в РФ (2014)².

Требования ФГОС

Федеральные государственные образовательные стандарты (далее – ФГОС) представляют собой совокупность требований, обязательных при реализации основных образовательных программ начального общего, основного общего, среднего (полного) общего, начального профессионального, среднего профессионального и высшего профессионального образования образовательными учреждениями, имеющими государственную аккредитацию.

Образовательный стандарт, являющийся отражением социального заказа, рассматривается разработчиками проекта как общественный договор, согласующий требования к образованию, предъявляемые семьей, обществом и государством, и представляет собой совокупность трех систем требований:

1. требования к структуре основных образовательных программ, в том числе требования к соотношению частей основной образовательной программы и их объѐму, а также к соотношению обязательной части основной образовательной программы и части, формируемой участниками образовательного процесса;

2. требования к условиям реализации основных образовательных программ, в том числе кадровым, финансовым, материально-техническим и иным условиям;

3. требования к результатам освоения основных образовательных программ.

Для учителя-предметника особенно важны требования к результатам освоения основных образовательных программ.

В Стандарте также сформулированы требования к трём видам результатов: личностным, предметным и метапредметным.

1. Требования к личностным результатам связаны с готовностью и способностью обучающихся к саморазвитию и личностному самоопределению, к целенаправленной учебно-познавательной деятельности. Эти требования включают сформированность качеств личности, описанных в «Портрете выпускника основной школы».

2. Требования к предметным результатам включают освоенные обучающимися специфические для изученной предметной области определённые теоретико-методологические знания, умения и виды деятельности для получения учебной информации, её преобразования и применения знаний в учебных, учебно-проектных и социально-проектных ситуациях.

Математика характеризуется как наука «о наиболее общих фундаментальных структурах реального мира, дающая важнейший аппарат и источник принципиальных идей для всех естественных наук и современных технологий». Её основные особенности:

• математика позволяет успешно решать практические задачи;

• математика – испытанное столетиями средство интеллектуального развития в условиях массового обучения (дедуктивный метод, решение системы задач и др.);

• математика обладает высоким воспитательным и коммуникативным потенциалом;

• математика – необходимый элемент предпрофессиональной подготовки.

3. Требования к метапредметным результатам включают:

• освоенные обучающимися межпредметные понятия и универсальные учебные действия, способность их использования в учебной, познавательной и социальной практике;

• самостоятельность планирования и осуществления учебной деятельности;

• организацию учебного сотрудничества с педагогами и сверстниками;

• построение индивидуальной образовательной траектории.

Структура учебной деятельности

Деятельность имеет собственную структуру, включающую взаимосвязанные элементы: мотивы (возникают на основе потребности), цели (конечный результат, на который преднамеренно направлена деятельность), действия (подчиняются целям) и операции (зависят от условий достижения конкретной цели). Цель не всегда совпадает с мотивом, но важно, чтобы цель стала мотивом деятельности, тогда у человека возникает стремление как можно лучше выполнить свою задачу, оно становится потребностью.

Учебная деятельность ученика характеризуется направленностью на достижение целей в процессе обучения, и как вид деятельности имеет аналогичную структуру, включая: учебные мотивы, учебные цели, учебные задачи, учебные действия (ориентировка, преобразование материала, контроль и оценка). Учебная деятельность осуществляется в рамках педагогической системы, которая включает:

1) субъект педагогического воздействия;

2) объект педагогического воздействия, становящийся субъектом в процессе этого воздействия;

3) предмет их совместной деятельности;

4) цели обучения;

5) средства педагогической коммуникации.

Процесс обучения существует только в совместной деятельности учителя и ученика, т. е. реализуется в единстве преподавания и учения. Он осуществляется в согласованном взаимодействии целей, содержания, форм, методов, средств обучения — всех компонентов методической системы обучения.

В процессе учебной деятельности ученик осуществляет познавательную деятельность, нацеленную на понимание учебной информации, которая является отражением адаптированных научных знаний, поэтому говорят об учебно-познавательной деятельности обучающегося (рисунок 1).

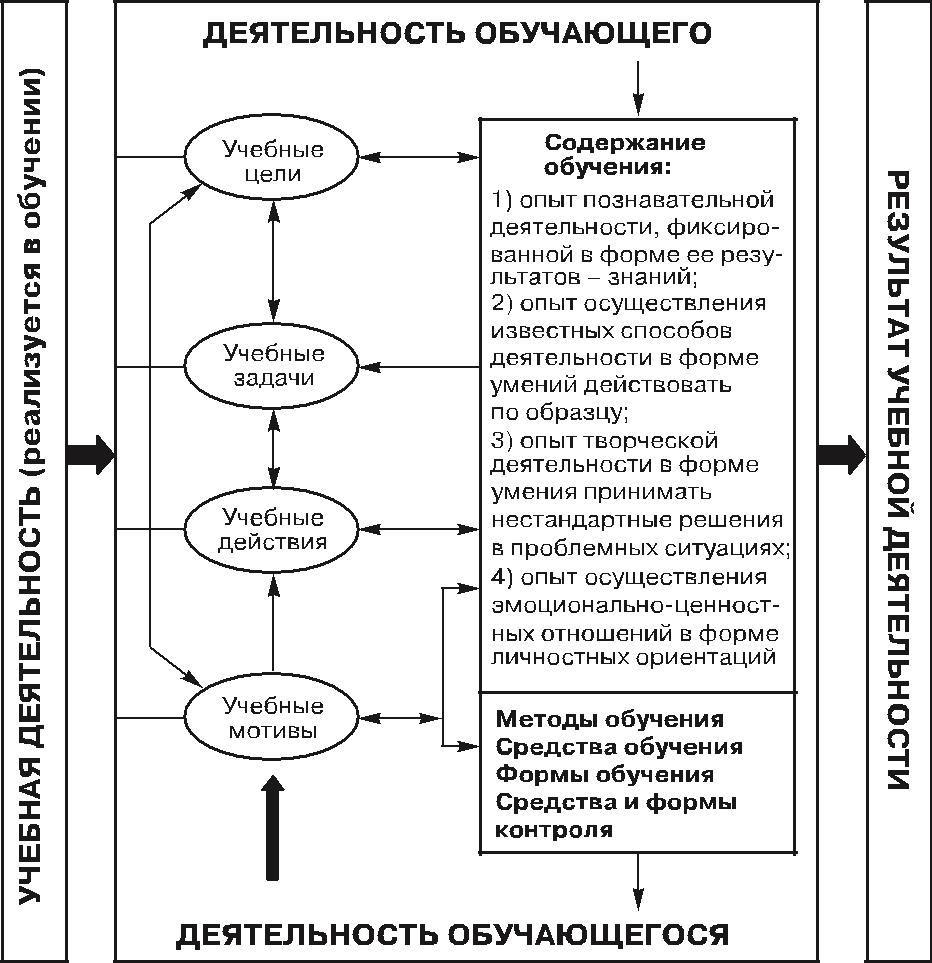
Рисунок 1. Структура учебной деятельности.

Все компоненты учебной деятельности тесно взаимосвязаны. Например, деятельность обучающего направлена на:

• организацию положительной учебной мотивации обучающихся через использование всех компонентов методической системы обучения;

• организацию достижения результата деятельности, т.е. на достижение цели через организацию учителем решения учебных задач учащимися посредством выполнения ими определённых учебных действий.

Деятельность обучающегося направлена, через собственную мотивацию, на достижение целей посредством решения учебных задач с помощью определённых учебных действий. Выполнение этих действий обеспечивает усвоение содержания образования, рассматриваемое в соответствии с культурологическим подходом, и достижение результата учебно-познавательной деятельности. Умение учиться предполагает полноценное освоение всех компонентов учебной деятельности.

Системно-деятельностный подход

В Стандарте указано, что в основе его реализации лежит системно-деятельностный подход.

Системно-деятельностный подход – это организация учебного процесса, в котором главное место отводится активной и разносторонней, в максимальной степени самостоятельной познавательной деятельности школьника. 

Системно-деятельностный подход является основой Стандарта и обеспечивает:

• формирование готовности к саморазвитию и непрерывному образованию;

• проектирование и конструирование социальной среды развития обучающихся в системе образования;

• активную учебно-познавательную деятельность обучающихся;

• построение образовательного процесса с учетом индивидуальных возрастных, психологических, физиологических особенностей обучающихся.

Цель учебной деятельности заключается в раскрытии смысла самого процесса учения, а именно, научить детей «умению учиться», что достигается за счет вполне определённой структуры учебной деятельности, включающей в себя учебные мотивы, учебную цель, учебную задачу, учебные действия и операции.

При организации учебно-познавательной деятельности учитель воссоздает опыт познавательной деятельности, накопленный человечеством, опыт, кристаллизующийся в виде знания о мире в широком значении этого слова.

Итак, в настоящее время в соответствии с общей целью образовательной системы преобладающей формой управления этой системой должно быть не внешнее взаимодействие субъектов образовательного процесса, а управление субъекта собственной активностью. Это возможно только в условиях реализации деятельностного подхода в обучении.

Таким образом, системно-деятельностный подход наиболее полно описывает структуру учебной деятельности учащихся. Результат его использования в обучении – становление обучающегося субъектом собственной учебной деятельности.

Субъект обучения – ученик, который:

1) не только активно усваивает (или даже «присваивает») новые знания и умения, но и соотносит их с содержанием собственного опыта, накопленного как в процессе предшествующего обучения, так и в жизненной практике;

2) регулирует процесс своей познавательной деятельности, контролирует и корректирует её результаты на основе рефлексии причин собственных успехов, ошибок, сомнений;

3) регуляция и рефлексия направлены как на рационально-логические операциональные, так и на личностно-смысловые аспекты этой деятельности.

Заключение

В обучении математике при переходе на новые ФГОС перемены необходимы, но для достижения требуемых результатов следует, в первую очередь, более полно использовать уже существующий потенциал нашего образования, в содержании которого уже давно присутствует деятельностная часть. Нужно лишь усилить акценты на соответствующем содержании и более широко использовать уже разработанные технологии, базирующиеся на деятельностном подходе.

Обучение должно быть организовано так, чтобы целенаправленно вести за собой развитие, направленное на решение задач проектной формы организации обучения, в котором важным является:

• применение активных форм познания: наблюдение, опыты, учебный диалог и прочее;

• создание условий для развития рефлексии — способности осознавать и оценивать свои мысли и действия как бы со стороны, соотносить результат деятельности с поставленной целью, определять своё знание и незнание и др.

Школа теперь выступает не столько источником информации, сколько учит учиться; учитель становится не проводником знаний, а личностью, обучающей способам творческой деятельности, направленной на самостоятельное приобретение и усвоение новых знаний.

Литература:

1. Приказ Минобрнауки России от 06.10.2009 г. № 413 «Об утверждении и введении в действие Федерального Государственного образовательного стандарта среднего общего образования».

2. Приказ Минобрнауки России от 17.12.2010 г. № 1897 «Об утверждении Федерального Государственного образовательного стандарта основного общего образования».

3. «Концепция развития математического образования в Российской Федерации», утверждена распоряжением Правительства РФ от 24.12.2013 г.

4. «Информация для родителей по ФГОС».

5. Л.И. Боженкова. Методика формирования универсальных учебных действий при обучении алгебре.

1^ http://zakon-ob-obrazovanii.ru

2^ http://www.firo.ru/wp-content/uploads/2014/12/Concept_mathematika.pdf

7