Муниципальное казенное общеобразовательное учреждение
"Гебинская средняя общеобразовательная школа им. Абакарова Г.А"
ОТКРЫТЫЙ УРОК
 по алгебре в 7 классе на тему
по алгебре в 7 классе на тему
«ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ»
Провела:учитель математики
МКОУ "Гебинская СОШ им. Абакарова Г.А."
Гаджиева Шахризат Магомедовна
Цель урока: научить учащихся применять формулы сокращенного умножения при выполнении упражнений различной сложности и творческих заданий.
Тип урока: урок обобщения и систематизации знаний
Оборудование: демонстрационный материал, карточки с заданиями, раздаточный материал, тесты в печатном виде, формулы сокращённого умножения.
Методы: словесный, репродуктивный, объяснительно-иллюстративный, проблемное изучение , практические, конструктивный или творческий.
Формы организации познавательной деятельности учащихся: фронтальный опрос, работа в парах, индивидуальная, коллективная, самостоятельная работа учащихся.
Ход урока:
1).Организационный момент.
- Здравствуйте, ребята. Садитесь. На предыдущих уроках вы познакомились с формулами сокращенного умножения. Сегодня мы продолжим эту тему. Вы покажете, как вы знаете эти формулы, как умеете их применять. Запишите в тетрадях число и тему урока.
Девиз урока: «Чему бы ты ни учился, ты учишься для себя». (Петроний)
2) Актуализация знаний:
Ребята, формулы сокращенного умножения имеют широкое применение в математике, особенно в старших классах. Их используют при решении уравнений, раскрытии скобок, разложении многочленов на множители, нахождении значений выражений. Поэтому надо хорошо знать эти формулы и уметь применять их в преобразованиях выражений.
а) А сейчас мы начнем наш путь с повторения формул и правил. На доске записана левая честь формулы, нужно продолжить формулу, назвать её и рассказать правило.(7 учеников)
| а2 – в2 = (а – в)(а + в) разность квадратов двух выражений | Разность квадратов двух выражений равна произведению их разности на их сумму. |
| (а + в) 2 = а2 + 2ав + в2
квадрат суммы двух выражений | Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого выражения на второе и плюс квадрат второго выражения. |
| (а – в) 2 = а2 – 2ав + в2
квадрат разности двух выражений | Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого выражения на второе и плюс квадрат второго выражения. |
| (а + в) 3 = а3 + 3а2в + 3ав2 + в3
куб суммы двух выражений | Куб суммы двух выражений равен кубу первого выражения, плюс утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение первого выражения на квадрат второго, плюс куб второго выражения. |
| (а – в) 3 = а3 – 3а2в + 3ав2 – в3 куб разности двух выражений | Куб разности двух выражений равен кубу первого выражения, минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение первого выражения на квадрат второго, минус куб второго выражения. |
| а3 + в3 = (а + в)(а2 – ав + в2)
сумма кубов двух выражений | Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности. |
| а3 – в3 = (а – в)(а2 + ав + в2)
разность кубов двух выражений | Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы. |
б)Найти куб и квадрат выражений, найти произведение одночленов, найти удвоенное произведение одночленов, найти утроенное произведение первого выражения на квадрат второго, найти утроенное произведение квадрата первого выражения на второе: ( устный счет)
2a b; 0,1b и 0,2k; m и 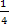 n; x2 и 2y2 ; 11ax и 3by; – 4b и – 7a; 2ab и 5n; ab3 и m3n4 .
n; x2 и 2y2 ; 11ax и 3by; – 4b и – 7a; 2ab и 5n; ab3 и m3n4 .
3)Обобщение и систематизация знаний.
ЗАДАНИЕ №1: Тест – соответствие (работа в парах). Расшифровка. Для каждого выражения из левого столбца подберите ему тождественно равное в правом: («5» - все верно, «4» - 1- 2 ошибки, «3» - 3 ошибки)
| № формулы | формула | № ответа | ответ | буква |
| 1 | (x+3)² | 1 | 4x²-9 | О |
| 2 | x²-16 | 2 | 16x²-40xy+25y² | А |
| 3 | (2x-3)(2x+3) | 3 | (x-4)(x+4) | И |
| 4 | 81-18x+x² | 4 | (3y+6x)² | Т |
| 5 | (4x-5y)² | 5 | x²+6x+9 | Д |
| 6 | 25x²-49y² | 6 | (9-x)² | Ф |
| 7 | 9y²+36yx+36x² | 7 | (5x-7y)(5x+7y) | Н |
Каждый ученик получает карточку, выполняет задание, получает соответствия:
1→5(Д), 2→3(И), 3→1(О), 4→6(Ф), 5→2(А), 6→7(Н), 7→4(Т).
Молодцы ребята, вы получили имя великого математика. Показываю его портрет.
Историческая справка: рассказ ученика. (Южиков Алексей). Очень давно, в Древней Греции жили и работали замечательные ученые-математики, которые всю свою жизнь отдали служению науке. В то время, все алгебраические утверждения выражали в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, а произведение двух чисел сравнивали с площадью, трех чисел-с объемом и т.д. первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям был древнегреческий ученый-математик, живший в 3 веке до нашей эры Диофант. Появились формулы, которые стали называться формулами сокращенного умножения.
ЗАДАНИЕ №2: Замените 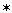 одночленом так, чтобы получившееся равенство было тождеством. (Индивидуальное задание.) Взаимопроверка. («5» - все верно, «4» - 1- 2 ошибки, «3» - 3 ошибки)
одночленом так, чтобы получившееся равенство было тождеством. (Индивидуальное задание.) Взаимопроверка. («5» - все верно, «4» - 1- 2 ошибки, «3» - 3 ошибки)
Ответы:
| 1 | 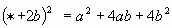
| a |
| 2 | 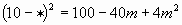
| 2m |
| 3 | 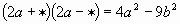
| 3b |
| 4 | 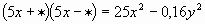
| 0,4y |
| 5 | 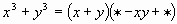
| x2, y2 |
| 6 | 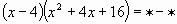
| x3, 64 |
- Какими формулами вы пользовались в данном задании?
ЗАДАНИЕ №3: Игра “Алгебраическая мозаика”. Составить из предложенных выражений формулы. Кто больше.
3х, 5у, 3х, 5у, 9х2, 30ху, 27х3, 125х2, 15ху, 25у2 , 125у3 .
Ответы: (Всего 7 формул. («5» - все верно, «4» - 1- 2 ошибки, «3» - 3 ошибки)
(3х + 5у)2 = 3х2+30ху+25у2
(3х – 5у)(3х + 5у) = 9х2– 25у 2
27х3 + 125у3 = (3х + 5у)(9х2+ 15ху+25у2)
(5у – 3х)2 = 25у2 – 30ху + 9х2
4)Контроль знаний. Следующий тест проверит ваше умение применять формулы сокращенного умножения при вычислении значений выражений и разложении на множители. Ваша цель – выбрать правильный ответ и записать нужную букву.
Учащиеся получают карточки с пятью заданиями. При правильных ответах из выбранных букв должно получиться слово «ВЕРНО».
Вариант 1:
1)Вычисли: 412 – 312
б) 72
в) 720
г) 730
2)Вычисли: 262 – 742
е) – 4800
ж) 4800
з) – 480
3)Разложи на множители: a4 – 8a2 + 16
c) (a2 + 4)2
n) (a – 4)2
p) (a2 – 4)2
4)Разложи на множители: a6 – 8
н) (а2 – 2) (а4 + 2а2 + 4)
к) (а3 – 4) (а3 + 4)
л) (а2 – 2) (а2 + 2а + 4)
5)Разложи на множители: 25b2 – 16c4
a) (5b – 4c2)2
o) (5b – 4c2) (5b + 4с2)
д) (5b – 4c) (5b + 4c)
Вариант 2:
1)Вычисли: 762 – 242
а) – 520
в) 5200
c) 52
2)Вычисли: 832 –732
e)1560
ж) 156
з) 1540
3)Разложи на множители: 4 + 4b2 + b4
к) (2 – b2)2
п) (2 + b)2
р) (2 + b2)2
4)Разложи на множители: 1 – c9
н) (1 – c3) ( 1 + c3 + c6)
м) (1 – c3 ) ( 1 + c3)
л) (1 – с3) ( 1 + 2с3 + с6)
5)Разложи на множители: 36x4 – 49y2
e) (6x2 – 7y)2
o) (6x2 – 7y) (6x2 + 7y)
a) (6x – 7y) (6x + 7y)
й на «3» 3 любых пары, «4» - 4 пары, «5» заполнена вся таблица. Учить формулы и правила.
| 1 и 2 выражения | Многочлен равный квадрату суммы этих выражений | Многочлен равный квадрату разности этих выражений | Многочлен равный кубу суммы этих выражений | Многочлен равный кубу разности этих выражений | Разность квадратов этих выражений |
| -5а и b |
|
| | | |
| 3а и 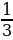 b b | | | | | |
| 5а2 и 0,2b2 | | | | | |
| a2b и –4 | | | | | |
| 6 и х2у2 | | | | | |
6)Итог урока.
- Итак, ребята урок подошел к концу.
Стих: (Климов Сергей)
Наук так много на земле,
У всех – своя тематика.
Но есть одна из них милей,
Зовётся математикой.
В ней не бывает скользких мест,
Всё строго в ней доказано,
И с нею движется прогресс,
И этим нам всё сказано.
- Оценка ваша за урок будет в оценочном листе, который вы мне сейчас сдадите. Сложите все 5 оценок и разделите на 5, это и будет ваша оценка за урок. Ребята, достигли ли Вы своей цели на этом уроке? В оценочном листе подчеркните свой ответ.
7)Рефлексия. В оценочном листе продолжи одно из предложений:
“Мне понятно…
“Я запомнил…
“Мне на уроке…
“Я думаю…
- Урок закончен. До свидания







 по алгебре в 7 классе на тему
по алгебре в 7 классе на тему
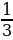 b
b









