оценочные средства по предмету
вероятность и статистика 7-9 классы
практические работы
на 2024-25уч.г.
Целью проведения практических работ является приобретение компетенций использования теоретических знаний при решении практических задач по теории вероятностей и статистике
Кодификатор проверяемых элементов содержания и распределение заданий по позициям кодификатора
| Код | № зада ния | Проверяемые виды деятельности | Уровень сложност и задания | Максима льный балл за задание |
| 6.1 | 1 | Извлекать информацию, представленную в таблицах | Б | 1 |
| 2 | Извлекать информацию, представленную в диаграммах и графиках | Б | 1 |
| 3 | Интерпретация и анализ, извлечённой информации | Б | 1 |
| 7.6 | 4 | Выполнение арифметических действий, с полученными числовыми данными | П | 2 |
| 5 | Определение процентов по диаграмме | П | 2 |
Критерии оценивания.
-2 балла за задание выставляется, если, дано правильное решение задачи, подробная аргументация своего решения, хорошее знание теоретических аспектов решения
- 1 балл за задание выставляется, если, правильное решение задачи, достаточная аргументация своего решения, хорошее знание теоретических аспектов решения, но допущены 2-3 неточности, но получен верный ответ
-0 баллов выставляется, если приведено неправильное решение задачи, отсутствие необходимых знания теоретических аспектов решения
Полученные баллы за выполнение всех заданий суммируются. Суммарный балл переводится в отметку по пятибалльной шкале с учётом рекомендуемой шкалы перевода:
| Отметка | «2» | «3» | «4» | «5» |
| Суммарный балл | 0-2 балла | 3-4 балла | 5-6 баллов | 7 баллов |
7 класс
Практическая работа №1 по теме «Диаграммы»
вариант 1
1. В таблице приведены площади некоторых материков и частей света.
Постройте столбиковую диаграмму, отражающую данные таблицы.
| Название | Европа | Азия | Африка | Северная Америка | Южная Америка | Австралия | Антарктида |
| Площадь | 10 | 44 | 30 | 24 | 18 | 8 | 14 |
2. На круговой диаграмме показано, как распределились учащиеся музыкальной школы по классам игры на различных музыкальных иструментах.
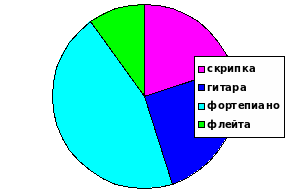
Используя диаграмму, ответьте на вопросы:
а) каким музыкальным инструментом занимаются учащиеся чаще всего?
Каким меньше всего?
б) найдите приближенно количество детей, занимающихся по классу гитары,
если в школе занимается 220 человек.
вариант 2
1. В таблице показано количество осадков, выпавших в течение недели (в миллиметрах).
Постройте столбиковую диаграмму, отражающую данные таблицы.
| День недели | Понедельник | Вторник | Среда | Четверг | Пятница | Суббота | Воскресенье |
| количество | 20 | 14 | 4 | 60 | 82 | 68 | 54 |
2. На круговой диаграмме показано, как распределились дети, посещающие школу искусств.
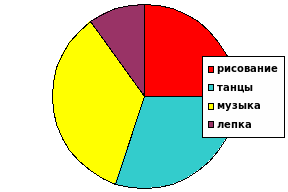
Используя диаграмму, ответьте на вопросы:
а) каким видом искусства занимаются дети чаще всего? Каким меньше всего?
б) найдите приближенно количество детей, занимающихся рисованием, если
в школе занимается 180 человек.
Практическая работа № 2 по теме «Средние значения»
вариант 1
1. Измерили массу 8 шоколадных батончиков и записали их массу:
33 г, 34 г, 35 г, 33 г, 38 г, 36 г, 40 г, 39 г.
а) расположите полученные значения по возрастанию.
б) найдите среднее значение массы.
2. Пользуясь результатами задачи 1, составьте таблицу отклонений показаний массы от среднего значения. Сколько показаний меньше, чем среднее? Сколько показаний больше, чем среднее?
3. Пользуясь результатами задачи 1, найдите медиану показаний массы батончиков.
Сколько показаний больше и сколько показаний меньше медианы?
вариант 2
1. В воду погрузили 8 термометров и записали их показания:
30º, 31º, 28º, 33º, 36º, 37º, 30º, 35º.
а) расположите полученные значения по возрастанию.
б) найдите среднее значение температуры.
2. Пользуясь результатами задачи 1, составьте таблицу отклонений показаний термометров от среднего значения. Сколько показаний меньше, чем среднее? Сколько показаний больше, чем среднее?
3. Пользуясь результатами задачи 1, найдите медиану показаний термометров. Сколько показаний больше и сколько показаний меньше медианы?
Практическая работа №3 по теме «Таблицы»
вариант 1
1. В таблице представлены города России с числом жителей по данным переписи населения в 2002 году.
| город
| население, тыс. чел.
|
| город
| население, тыс. чел.
|
| Волгоград | 1 013 | Нижний Новгород | 1 311 |
| Екатеринбург | 1 293 | Новосибирск | 1 426 |
| Казань | 1 105 | Ростов – на – Дону | 1 070 |
| Москва | 10 358 | Самара | 1 158 |
| Омск | 1 134 | Санкт – Петербург | 4 669 |
| Пермь | 1 000 | Челябинск | 1 078 |
| Уфа | 1 042 | Мурманск | 1 147 |
По данным таблицы укажите:
а) наименее населенные города (менее 1 100 тыс. жителей);
б) города, в которых более 3 тыс. жителей;
в) общее количество жителей в указанных городах.
2. Ученики класса указали животных, которые живут у них дома. Получился следующий список:
кошка, хомяки, кошка, кошка, рыбки, собака, ежик, собака, рыбки, кошка, черепаха, птички, кошка, собака, рыбки, рыбки, хомяки, птички, собака, кошка, рыбки, черепаха, собака, собака, ежик, черепаха, хомяки, птички, кошка, уж, черепаха, морская свинка, кошка, морская свинка, собака, кошка.
Составьте таблицу подсчета и таблицу распределения учеников по животным.
вариант 2
1. В таблице представлены города России с числом жителей по данным переписи населения в 1979 году.
| город
| население, тыс. чел.
|
| город
| население, тыс. чел.
|
| Волгоград | 926 | Нижний Новгород | 1 324 |
| Екатеринбург | 1 210 | Новосибирск | 1 309 |
| Казань | 989 | Ростов – на – Дону | 925 |
| Москва | 8 057 | Самара | 1 192 |
| Омск | 1 016 | Санкт – Петербург | 4 569 |
| Пермь | 1 089 | Челябинск | 1 030 |
| Уфа | 977 | Мурманск | 1 175 |
По данным таблицы укажите:
а) наиболее населенные города (более 1 300 тыс. жителей);
б) города, в которых менее 1 тыс. жителей;
в) общее количество жителей в указанных городах.
2. Ученики 7 класса указали предметы, которыми они увлекаются. Получился следующий список:
литература, география, литература, литература, труд, математика, история, литература, физика, русский язык, литература, математика, труд, труд, русский язык, математика, труд, литература, физкультура, математика, биология, география, русский язык, литература, музыка, история, физика, английский язык, математика, музыка, английский язык, литература.
Составьте таблицу подсчета и таблицу распределения учеников по предметам.
Практическая работа №4 «Случайная изменчивость»
вариант 1
Колебания напряжения в бытовых электрических сетях
Приведены результаты 25 измерений напряжения (в вольтах) в бытовой сети. Все измерения были сделаны в дневное время, в случайно (бессистемно) выбранные моменты времени.

225 В, 227 В, 225 В, 228 В, 225 В,
228 В, 218 В, 217 В, 218 В, 220 В,
223 В, 225 В, 216 В, 222 В, 224 В,
220 В, 218 В, 221 В, 220 В, 216 В,
214 В, 219 В, 231 В, 228 В, 227 В.
Электрические приборы в России рассчитаны на напряжение 220 В. При небольших отклонениях напряжения от 220 В они работают исправно, а при значительных колебаниях напряжения могут прийти в негодность.
В России номинальное напряжение в бытовых сетях 220 В. Как вы видите, реальное напряжение может отличаться от 220 В. Обычно напряжение либо немного выше этого значения, либо ниже. Это зависит от дополнительно включенных электроприборов. Моменты включения электроприборов является случайными и приводят к случайной изменчивости напряжения.
1.Какое самое большое напряжение было зафиксировано в период наблюдения?
2.Какое самое маленькое напряжение было зафиксировано?
3. Каков размах значений напряжения?
4. Какова медиана напряжения?
5. Каково среднее значение напряжения?
6. Заполните таблицу частот:
| Напряжение, В | 214 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 | 227 | 228 | 231 |
| Абсолютная частота | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Относитель- ная частота | 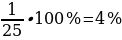
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построить гистограмму частот:
| Интервалы | 2-5 | 5-8 | 8-11 | 11-14 | 14-17 | 17-20 |
| Частота | 15 | 35 | 64 | 55 | 21 | 10 |


частота

интервалы
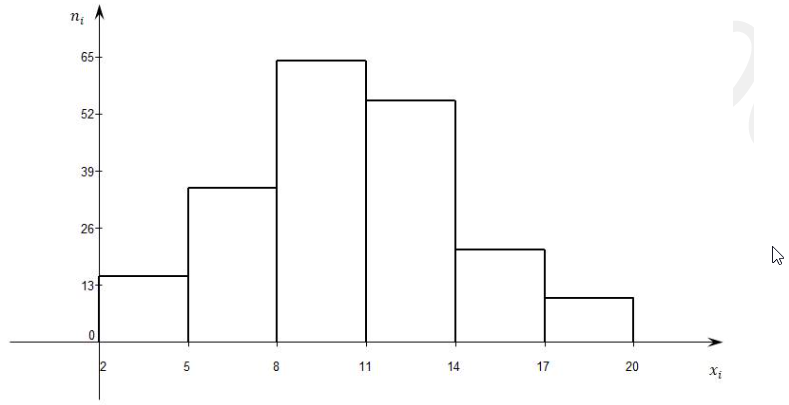
Сделайте вывод.
вариант 2
На участке дороги поставили радар для определения скорости проезжающих автомобилей. Были сделаны измерения:
132 км/ч, 136 км/ч, 123 км/ч, 68 км/ч, 83 км/ч,
68 км/ч, 94 км/ч, 86 км/ч, 108 км/ч, 117 км/ч,
128 км/ч, 125 км/ч, 54 км/ч, 117 км/ч, 56 км/ч,
86 км/ч, 56 км/ч, 86 км/ч,56 км/ч, 123 км/ч,
132 км/ч, 125 км/ч, 68 км/ч, 130 км/ч, 108 км/ч.
На загородных трассах максимальная разрешенная скорость движения для легковых автомобилей составляет 90 км/ч. За превышение или занижение этого показателя на водителя накладывают штраф. В 2023 году штрафы накладываются за превышение разрешенной скорости на 20 км/ч и более, причем, если водитель, наоборот, едет с заниженной скоростью, то штраф он получит вне зависимости от показателя отклонения от нормы скорости движения.
а) Какая самая большая скорость была зафиксирована в период наблюдения?
б) Какая самая маленькая скорость была зафиксирована?
в) Каков размах значений скорости?
г) Какова медиана скорости?
д) Каково среднее значение скорости?
е) Заполните таблицу частот:
| Скорость, км/ч | 54 | 56 | 68 | 83 | 86 | 94 | 108 | 117 | 123 | 125 | 128 | 130 | 132 | 136 |
| Абсолютная частота | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Относитель- ная частота | 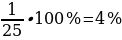
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построить гистограмму частот:
| Интервалы | 2-5 | 5-8 | 8-11 | 11-14 | 14-17 | 17-20 |
| Частота | 24 | 40 | 62 | 32 | 15 | 10 |

частота



интервалы
Сделайте вывод.
Практическая работа № 5 по теме «Частота выпадения орла»
1 этап.
Приготовьте монету. Чтобы определить, как часто при бросании монеты выпадает орел, будем подбрасывать монету и фиксировать число выпадений орла. Если выпал орел – ставьте черточку в первой строке, если решка – во второй строке. Бросьте монету 20 раз и заполните таблицу 1 (воспользуйтесь символом |||| ).
Таблица 1
| Сторона монеты | Выпало | Количество выпадений | Частота |
| Орел |
|
|
|
| Решка |
|
|
|
| Всего: | 20 |
|
2 этап.
а) Заполните последний столбец таблицы 1, определив частоту выпадения орла по формуле (все числа округлите до сотых):
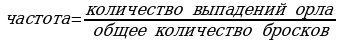 .
.
В данном эксперименте знаменатель во всех вычислениях равен 20 – общему числу бросков, а в числитель подставьте числа, полученные в опыте.
б) Предположите, какая теоретически должна быть частота выпадения орла при бросании монеты? ____________ Почему? _________________________________________ _____________________________________________________________________________
в) Сравните свои экспериментально полученные результаты с предполагаемым: ____ _____________________________________________________________________________
_____________________________________________________________________________
г) Как можно найти частоту появления решки в данном эксперименте? (Укажите два способа!) _____________________________________________________________________
Вывод. (Запишите вывод в тетрадь. Подсказка: Вывод пишется исходя из цели работы.)
В выводе ответьте на вопросы 1) Зависит ли полученный результат от длины серии эксперимента (количества бросков)? 2) Почему ваш результат может отличаться от 0,5?
8 КЛАСС
Практическая работа №1 "Опыты с равновозможными элементарными событиями".
Вариант 1.
№1. Подбросьте кубик, посмотрите, какие события произойдут.
а) Начертите таблицу в тетради и результаты впишите в таблицу
|
| Число выпавших очков на кубике в попытке |
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Кубик |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Посчитайте количество выпавших четных чисел и найдите частоту выпадения четного числа очков в вашем эксперименте. Частотой появления события A в данной серии испытаний называют отношение числа m наступлений данного случайного события в данной серии испытаний к общему числу n испытаний этой серии называется
P (A)=m/n.
в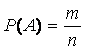 ) Вычислите вероятность выпадения четного числа очков, используя классическое определение вероятности.
) Вычислите вероятность выпадения четного числа очков, используя классическое определение вероятности.
Вероятность P(A) события А определяется по формуле
где m – число элементарных исходов, благоприятствующих A; n – число всех возможных элементарных исходов.
г) Сравните результаты пунктов б и в и сделайте вывод.
№2. Подбросьте два кубика, посмотрите, какие события произойдут.
а) Начертите таблицу в тетради и результаты впишите в таблицу
|
| Число выпавших очков на кубиках в попытке |
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 кубик |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 кубик |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Определите, какие события являются случайными, какие достоверными, а какие невозможными:
А = {на кубиках выпало одинаковое число очков}
В = {сумма очков на кубиках не превосходит 12}
С = {сумма очков на кубиках равна 11}
Д = {произведение очков на кубиках равно 11}
Вариант 2.
№1. №1. Подбросьте кубик, посмотрите, какие события произойдут.
а) Начертите таблицу в тетради и результаты впишите в таблицу
|
| Число выпавших очков на кубике в попытке |
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Кубик |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Посчитайте количество выпавших нечетных чисел и найдите частоту выпадения нечетного числа очков в вашем эксперименте. Частотой появления события A в данной серии испытаний называют отношение числа m наступлений данного случайного события в данной серии испытаний к общему числу n испытаний этой серии называется
P (A)=m/n.
в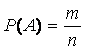 ) Вычислите вероятность выпадения нечетного числа очков, используя классическое определение вероятности.
) Вычислите вероятность выпадения нечетного числа очков, используя классическое определение вероятности.
Вероятность P(A) события А определяется по формуле
где m – число элементарных исходов, благоприятствующих A; n – число всех возможных элементарных исходов.
г) Сравните результаты пунктов б и в и сделайте вывод.
№2. Подбросьте два кубика, посмотрите, какие события произойдут.
Начертите таблицу в тетради и результаты впишите в таблицу
|
| Число выпавших очков на кубиках в попытке |
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 кубик |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 кубик |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определите: какие события являются случайными, какие достоверными, а какие невозможными.
А = {на кубиках выпало разное число очков}
В = {сумма очков на кубике больше 1}
С = {сумма очков на кубиках равна 13}
Д = {произведение очков на кубиках равно 12}
№3. Монету бросают три раза.
а) Запишите перечислением всех возможных элементарных исходов.
б) Запишите перечислением элементарных исходов событие А «ни разу не выпали две решки подряд».
Для орла и решки используйте обозначения О и Р.
в) Найдите вероятность события А «ни разу не выпали две решки подряд».
№4. Соревнования по фигурному катанию проходят 3 дня. Всего запланировано 50 выступлений: в первый день — 18 выступлений, остальные распределены поровну между вторым и третьим днями. В соревнованиях участвует спортсмен М. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что спортсмен М. будет выступать во второй день соревнований?
9 класс
Практическая работа №1 "Вычисление вероятностей с использованием комбинаторных функций электронных таблиц"
Цель работы: вычисление вероятностей событий по классической формуле определения вероятности с использованием формул комбинаторики, развитие самостоятельной мыслительной деятельности, вычислительных навыков, творческого мышления студентов.
Ход выполнения задания
1. Создать на рабочем столе папку (ФИ_класс_практическая работа №1)
2. Запустить программу для работы с электронными таблицами (Пуск-Программы-Microsoft Office-Excel).
3. Сохранить файл в папке (Файл - Сохранить как...- рабочий стол- ФИ_класс_практическая работа №1).
4. Переименовать «Лист1» в «Задание 1» (правой кнопкой мышки на ярлычке Листа 1, выбрать «Перименовать»).
5. Добавить «Лист 2», «Лист 3», «Лист 4», «Лист 5» и переименовать в «Задание 2», «Задание 3» и «Задание 4», «Задание 5» соответственно.
6. Выполнить задания из раздела «Задания для самостоятельного выполнения».
ОБРАЗЕЦ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
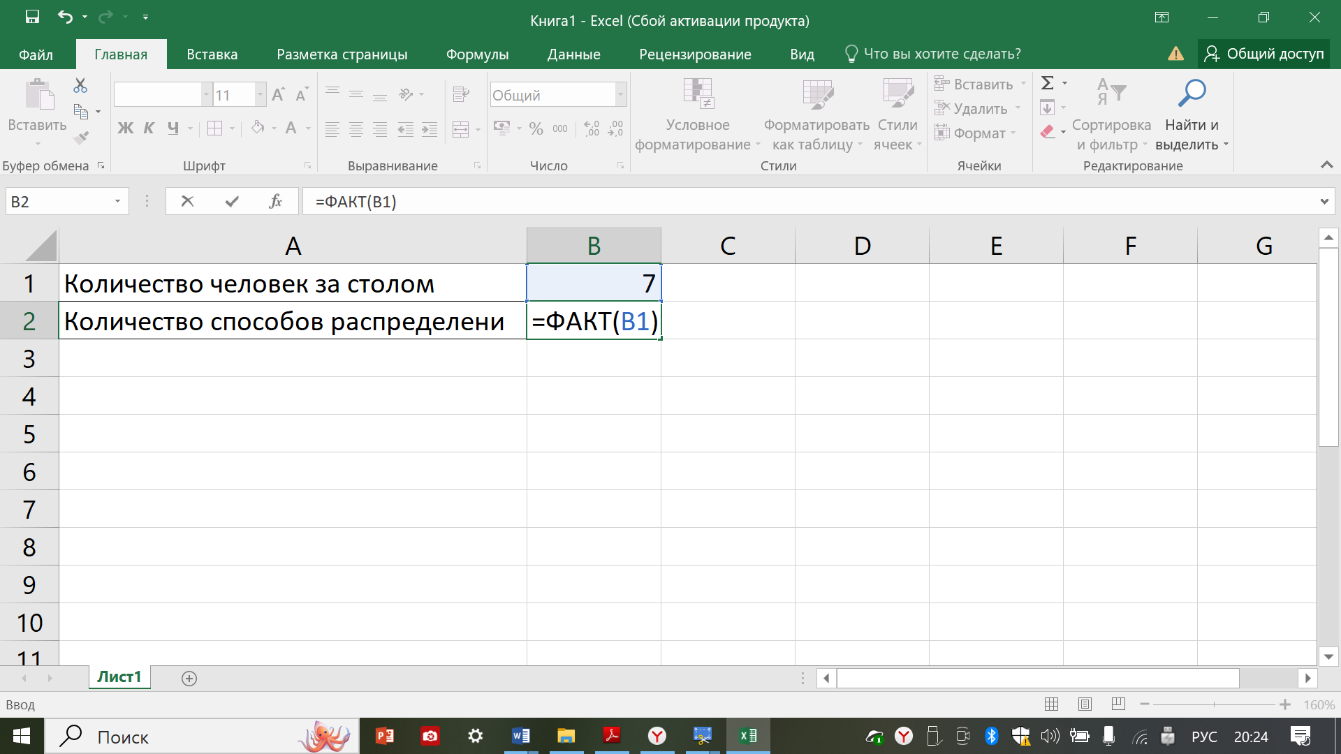
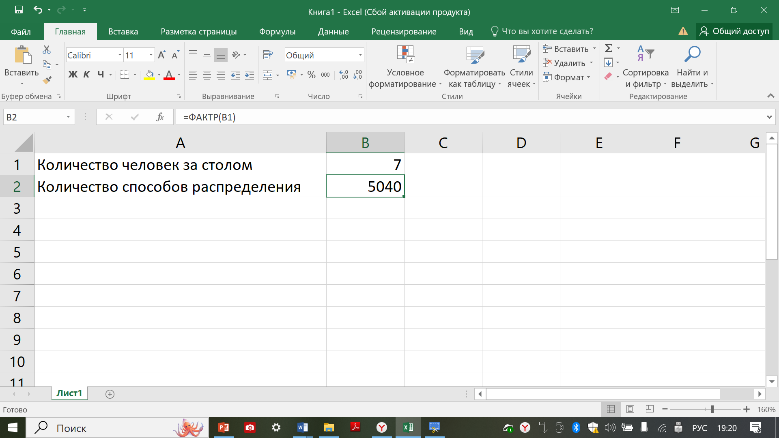
ПЕРЕСТАНОВКИ. Различные упорядоченные множества, которые отличаются лишь порядком элементов, то есть могут быть получены из того же самого множества перестановкой местами элементов, называются перестановками этого множества. Пример типовой задачи на вычисление перестановок: вокруг стола рассаживают 7 человек. Найти количество различных способов распраделения их за столом.
Вычисление перестановок можно выполнить с использованием функции ПЕРЕСТ(n;n). Заметьте, что обапараметра у данной функции в данном случае будут ссылаться на одну и ту же ячейку, так как количество элементов сохраняется. ИЛИ Вычисление перестановок можно выполнить с использованием функции ФАКТ(n).
1. На соответствующем листе введите заголовок в ячейку А1 («Количество человек за столом»), в ячейку А2 («Количество способов распределения»), в ячейку В1 – подставьте значения, указанные в примере выше.
2. В ячейку В2 введите формулу для вычисления сочетаний: = ФАКТ(В1)
!!! Обратите внимание, что ячейки, в которых находится не просто текст, число, а именно формула, позволяющая выводить динамическое содержимое в данную ячейку, начинается обязательно со знака «=». Только в этом случае программа идентифицирует текст как формулу и будет производить вычисления.
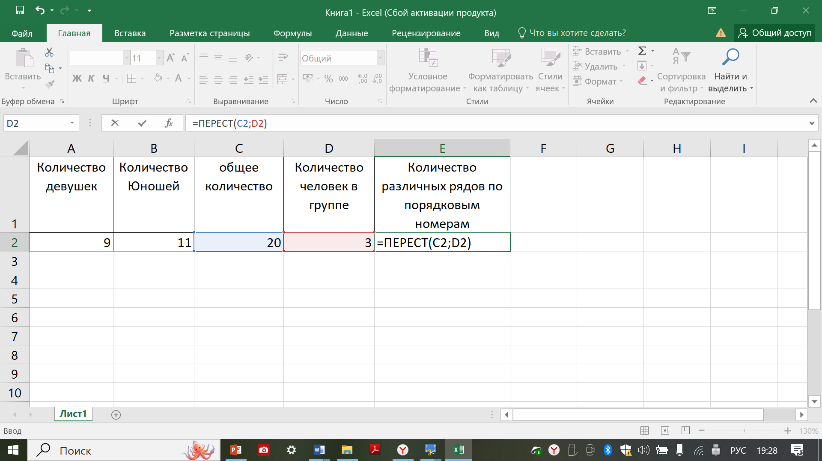
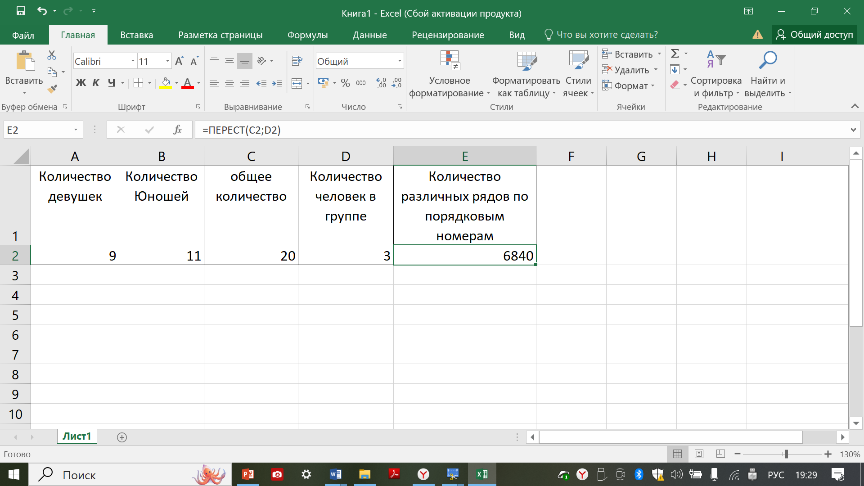
РАЗМЕЩЕНИЕ. Различные упорядоченные k-элементные подмножества множества из n элементов называются размещениями из n элементов по k. Размещения отличаются друг от друга либо элементами, либо их порядками следования. Пример типовой задачи на вычисление размещений: в группе 9 девушек и 11 юношей. Для представительства этой группе на форуме выбирают 3 человек, которых по присвоенным в процессе выбора порядковым номерам выстраивают в ряд. Подсчитать количество рядов кторые можно постоить.
Вычисление размещений средствами MS Excel можно реализовать с применением функции ПЕРЕСТ(n;k), где n – число элементов исходного множества, а k – число элементов выбранного подмножества.
1. На соответствующем листе введите заголовок в ячейку А1 («Количество девушек»), в ячейку В2 («Количество юношей»), в ячейку С1 («Общее количество»), в ячейку D1 («Количество человек в группе»), в ячейку Е1 («Количество рядов по порядковым номерам»), в ячейки А2, В2, С2, D2– подставьте значения, указанные в примере выше.
2. В ячейку Е2 введите формулу для вычисления сочетаний: = ПЕРЕСТ (С2; D2).
СОЧЕТАНИЕ. Произвольное k-элементное подмножество данного множества из n элементов называется сочетанием из N элементов по k. порядок элементов в сочетании не существенен. Пример типовой задачи на сочетания: имеется 3 красные и 4 оранжевые гвоздики. Букет составляют из 5 цветков. Сколько можно составить различных букетов?
Число сочетаний можно вычислить с помощью функции ЧИСЛОКОМБ(n;k), которая относится к математическим функциям.
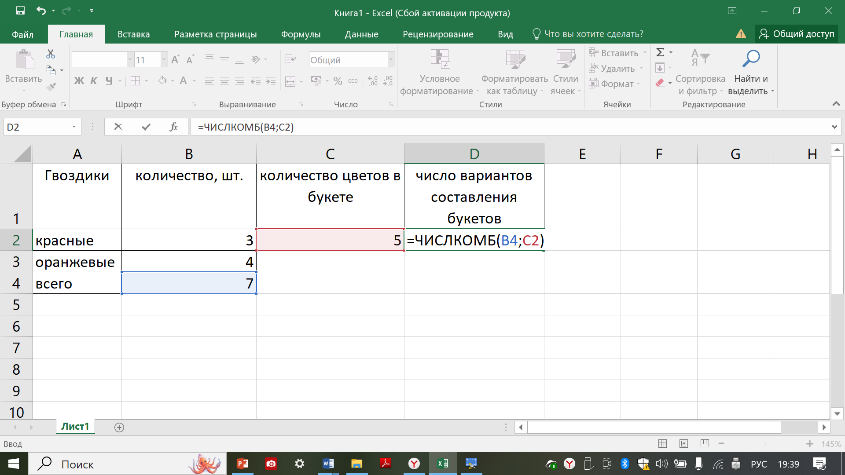
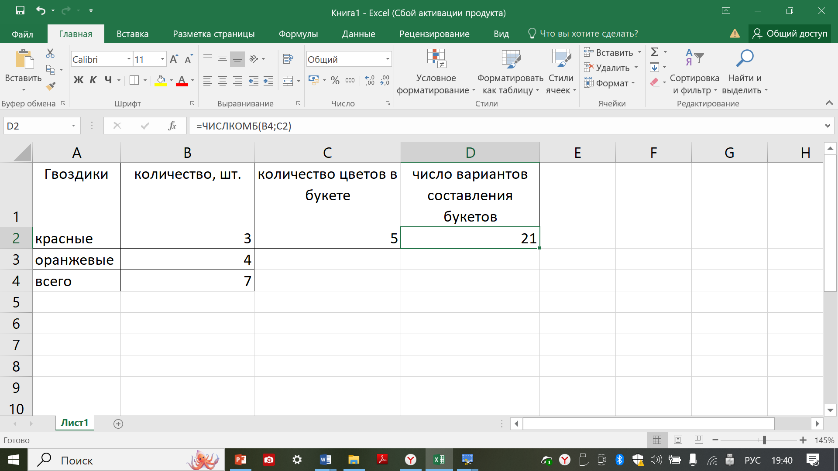
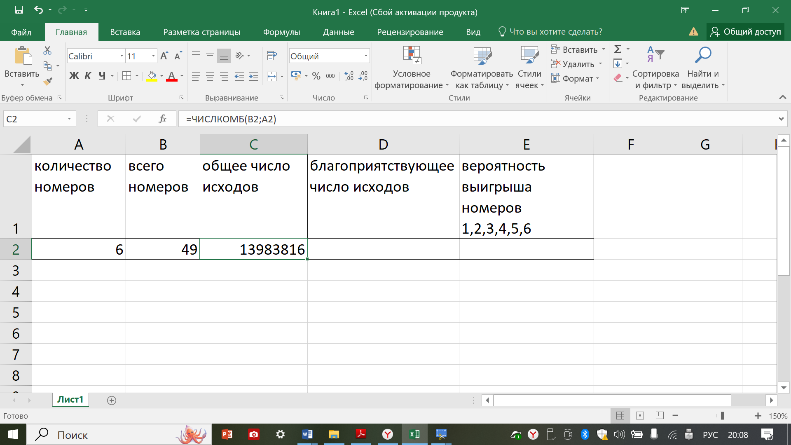
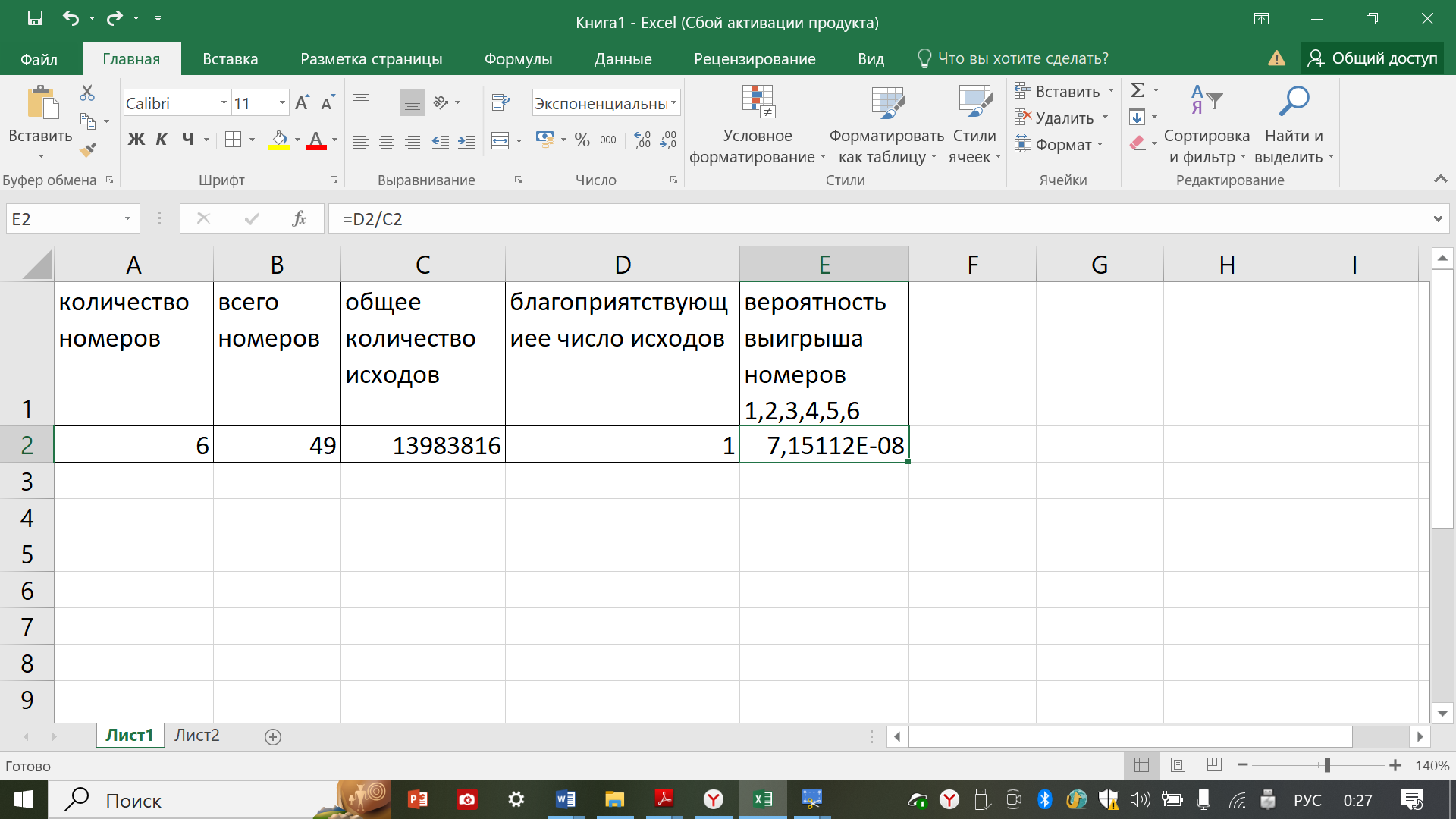
ВЕРОЯТНОСТЬ. Если эксперимент заканчивается одним из n равновозможных исходов, из которых т являются благоприятными для наступления данного события, то вероятность этого события равна т/n. В ячейку С2 мы будем вводить число, соответствующее общему количеству всех возможных исходов события, а в ячейку D2 – количество исходов, благоприятствующих появлению интересующего исхода. Для вычисления вероятности необходимо в ячейку Е2 ввести формулу, которая, по классическому определению вероятности, будет подсчитывать и выводить в данную ячейку результат деления благоприятствующего количества исходов на общее количество. Таким образом, формула в данной ячейке должна быть следующая: =В1/А1
Пример типовой задачи на вероятность: в тираже лотереи «Спортлото» разыгрывались 6 случайных номеров из 49. Какова вероятность того, что в тираже лотереи выиграют номера 1, 2, 3, 4, 5, 6?
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ
ВАРИАНТ 1
1. Сколькими способами можно расставить 8 участников финального забега на восьми беговых дорожках?
2. Сколькими способами 6 студентов, сдающих экзамен, могут занять места в аудитории, в которой стоит 20 одноместных столов?
3. Учащимся дали список из 10 книг, которые рекомендуются прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?
4. У вахтера в комнате доска с ключами. Всего 5 крючков, а на них 5 ключей. Доска упала и ключи рассыпались. Вахтёр собрал ключи и развесил их в случайном порядке. Какова вероятность того, что каждый ключ висит на своем месте?
5. В ящике 4 красных и 2 жёлтых флажка. Из него наудачу извлекают 3 флажка. Какова вероятность того, что все эти флажки красные?
ВАРИАНТ 2
1. Сколькими способами 9 человек могут встать в очередь в театральную кассу?
2. На страницах альбома 6 свободных мест для фотографий. Сколькими способами можно вложить в свободные места 4 фотографии?
3. Из набора, состоящего из 15 красок, надо выбрать 3 краски для окрашивания шкатулки. Сколькими способами можно сделать этот выбор?
4. Слово «АПЕЛЬСИН» написали на полоске картона и разрезали полоску на буквы. Девочка, играя, выложила буквы в ряд в случайном порядке. Найдите вероятность того, что получилось слово «СПАНИЕЛЬ»?
5. В коробке 2 белых и 3 черных шаров. Из неё наудачу извлекают 2 шарика. Какова вероятность того, что все эти шарики черные?
Практическая работа №2 «Испытания Бернулли»
Цель: формирование умений решать задачи на нахождение вероятности с использованием формулы Бернулли.
Ход практической работы Повторим теоретический материал
Если производится n независимых испытаний, в каждом из которых вероятность появления события А одна и та же и равна p, то вероятность того, что событие А появится в этих n испытаниях m раз, выражается формулой Бернулли
Pn(m) = Cnk·pm·qn-m, где q = 1-p.
Рассмотрим образцы решения задач
Задача 1.
В урне 20 белых и 10 черных шаров. Вынули подряд 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Какова вероятность того, что из четырех вынутых шаров окажется два белых?
Решение. Вероятность извлечения белого шара p=20/30=2/3 можно считать одной и той же во всех испытаниях; q=1-p=1/3. Используя формулу Бернулли, получаем
P4(2) = C42·p2·q2=6 (2/3)2·(1/3)2 = 8/27 Ответ: 8/27
Задача 2. Игральную кость бросили 10 раз. Какова вероятность, что число 3 выпадет два раза?
Решение. При одном броске вероятность выпадения тройки равна р = 1/6, а вероятность не выпадения равна 1-р = 5/6.
Каждый бросок - независимое испытание. Применим ф-лу Бернулли.
Рn(m)=Сnm pm(1-p)n-m, где n=10, m=2
Р= С102 ·(1/6)2 ·(5/6)8 = 10!/ (8!*2!)* 58/610 = 45*58/610 ≈0,29. Ответ: 0,29
Задача 3. Вероятность появления события А равна 0,4. Какова вероятность того, что при 10 испытаниях событие А появится не более трех раз?
Решение. Здесь p=0,4, q=0,6. Имеем:
P10(0) = q10, P10(1) = 10pq9, P10(2) = 45p2q8, P10(3) = 120p3q7.
Вероятность того, что событие А появится не больше трех раз, равна
Р = P10(0) + P10(1) + P10(2) + P10(3) = q10+10pq9+45p2q8+120p3q7≈ 0,38 Ответ: 0,38
Задачи для самопроверки
Вариант 1
Задача 1. Монету бросают 10 раз. Найдите вероятность, что герб выпадет 3 раза;
Задача 2. Игральная кость бросается 6 раз. Какова вероятность того, что шестерка выпадет 4 раза?
Задача 3. Вероятность изготовления нестандартной детали равна 0.11. Пользуясь формулой Бернулли найти вероятность того, что из пяти наудачу взятых деталей будут четыре стандартных.
Вариант 2
Задача 1 . Найти вероятность того, что событие А появится не менее трёх раз в пяти испытаниях, если вероятность появления события А в одном испытании равна 0,4
Задача 2. Вероятность всхожести семян пшеницы равна 0,9. Какова вероятность того, что из четырёх посеянных семян взойдут не менее трёх?
Задача 3 В семье 5 детей. Найти вероятность того, что среди детей более трёх мальчиков. Вероятность рождения мальчика равна 0,7?










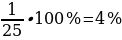





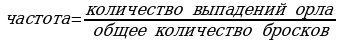 .
.

















