Подготовка к ОГЭ -Задание 25

Геометрическая задача № 25 ОГЭ

(задача на доказательство)

Характеристика задания

Задание 25 ОГЭ по математике представляет собой планиметрическую задачу на доказательство, связанную со свойствами треугольников, четырёхугольников, окружностей. Во многих случаях доказательство может быть проведено несколькими способами.

Сущность доказательства состоит в построении такой последовательности ранее доказанных и принятых в математике утверждений, прямым логическим следствием которых является утверждение, которое нужно было доказать. Вообще,  доказать какое-либо утверждение – это значит показать, что утверждение является логическим следствием системы уже доказанных и принятых в науке   утверждений.

Задача №25

Баллы

Содержание критерия

2

Доказательство верное, все шаги обоснованны

1

Доказательство в целом верное, но содержит неточности

0

Решение не соответствует ни одному из критериев, перечисленных выше

2

Максимальный бал

• Задания, оцениваемые в 2 балла, считаются выполненными верно, если обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется первичный балл.
• Нужно нацеливать учащихся на лаконичность и не требовать подробных комментариев и формулировок теорем, при этом в решении должны быть ссылки на теоремы, чтобы показать, что ученик владеет теоретическим материалом.
• Если в решении допущена ошибка непринципиального характера (вычислительная, погрешность в терминологии, или символике и др.) , не влияющая на правильность общего хода решения (даже при неверном ответе) и, позволяющая не смотря на её наличие, сделать вывод о владении материалом, то учащемуся засчитывается балл .

(из рекомендаций ФИПИ)

Трудности решения геометрических задач

• Неалгоритмичность задач
• Необходимость выбора метода решения задачи и теоремы для решения конкретной задачи (нескольких теорем) из большого набора известных фактов
• Нужно решить довольно много задач, чтобы научиться их решать.

Необходимые условия успеха при решении задач по геометрии

• Уверенное владение основными понятиями и их свойствами (определения, аксиомы, теоремы, базовые задачи)
• Знание основных методов решения задач
• Умение комбинировать методы решения задач
• Наличие опыта решения задач

Причины ошибок в решении

геометрических задач

• Невнимательное чтение условия и вопроса

задания

• Недостатки в работе с рисунком
• Принятие ошибочных гипотез
• Незнание и/или непонимание аксиом,

определений, теорем

• Неумение их применять
• Нарушения логики в рассуждениях
• Вычислительные ошибки

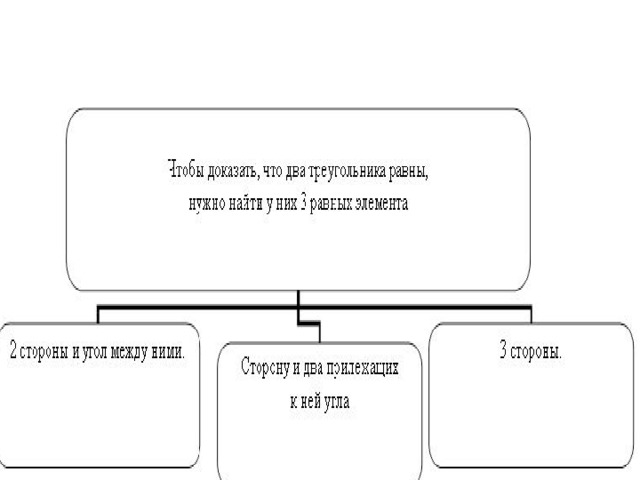
Основные умения:

• умение делать чертеж к задаче;
• умение записывать условие и требование задачи;
• умение «видеть» то, что изображено на чертеже;
• умения выполнять дополнительные построения;
• умения выбирать метод решения.

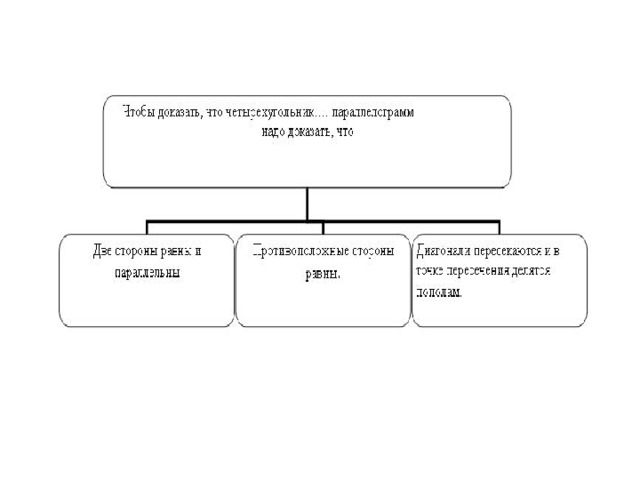
Некоторые методы решения геометрических задач

• Метод подобия
• Метод площадей
• Метод дополнительных построений
• Метод вспомогательной окружности

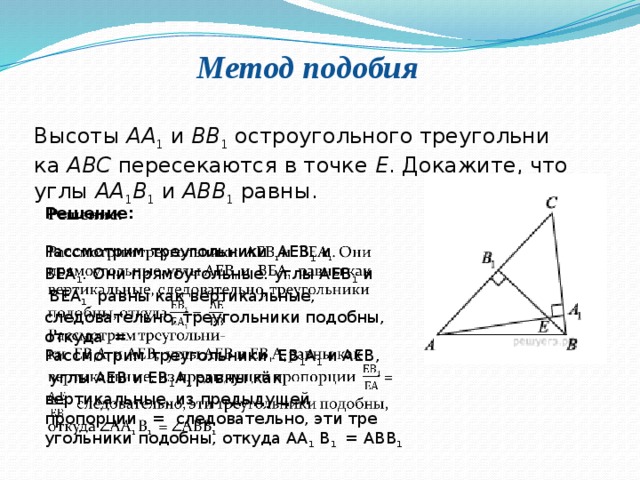
Метод подобия

Высоты  AA 1  и  BB 1  ост­ро­уголь­но­го тре­уголь­ни­ка  ABC  пе­ре­се­ка­ют­ся в точке  E . Докажите, что углы  AA 1 B 1  и  ABB 1  равны.

Решение:

Рассмотрим тре­уголь­ни­ки  АЕВ 1  и  ВЕА 1 . Они прямоугольные. углы АЕВ 1  и  ВЕА 1  равны как вертикальные, следовательно, тре­уголь­ни­ки подобны, от­ку­да  =

Рас­смот­рим тре­уголь­ни­ки  ЕВ 1 А 1  и АЕВ,  углы АЕВ и ЕВ 1 А 1 равны как вертикальные, из предыдущей пропорции  = следовательно, эти тре­уголь­ни­ки подобны, от­ку­да АА 1 В 1 = АВВ 1

Метод площадей

Внутри па­рал­ле­ло­грам­ма  ABCD  вы­бра­ли про­из­воль­ную точку  E . Докажите, что сумма пло­ща­дей тре­уголь­ни­ков  BEC  и  AED  равна по­ло­ви­не пло­ща­ди параллелограмма.

Решение:

Проведем от­ре­зок KN  пер­пен­ди­ку­ляр­ный сто­ро­нам AD и BC про­хо­дя­щий через точку  E. Пло­щадь па­рал­ле­ло­грам­ма S ABCD = AD · KN

  Пло­щадь тре­уголь­ни­ка  S AED = AD · EN. Пло­щадь тре­уголь­ни­ка  S BEC = EK · BC. Получаем, что сумма пло­ща­дей тре­уголь­ни­ков  и  равна:

S AED + S BEC AD · EN + EK · BC = AD (EN + EK)=

= AD · NK =  S ABCD

Метод дополнительных построений

Точка  K  — се­ре­ди­на бо­ко­вой сто­ро­ны  CD  тра­пе­ции  ABCD . Докажите, что пло­щадь тре­уголь­ни­ка  KAB  равна по­ло­ви­не пло­ща­ди трапеции

Решение. Продолжим  BK  до пе­ре­се­че­ния с пря­мой  AD  в точке  F . Заметим, что в тре­уголь­ни­ках  FDK  и  BCK  сто­ро­ны  CK и  DK  равны по условию, углы при вер­ши­не K равны как вертикальные, а углы  KDF  и  KCB  равны как на­крест лежащие. Значит, тре­уголь­ни­ки  FDK  и  BCK  равны.

Следовательно, их пло­ща­ди равны, то есть пло­щадь тра­пе­ции равна пло­ща­ди тре­уголь­ни­ка  ABF . Но из ра­вен­ства тре­уголь­ни­ков также вытекает, что  FK = BK , то есть  AK  — ме­ди­а­на в тре­уголь­ни­ке  ABF . Тогда треугольник  KAB  по пло­ща­ди со­ста­вит по­ло­ви­ну тре­уголь­ни­ка  FAB , а значит, и дан­ной трапеции.

Метод вспомогательной окружности

В остроугольном треугольнике  ABC  проведены высоты АА 1  и СС 1.  Докажите, что углы СС 1 А 1 и САА равны.

Решение:

Треугольники АА 1 С и СС 1 А имеют общую гипотенузу АС. Поэтому точки А, С, А 1 , С 1 лежат на одной окружности. Углы СС 1 А 1 и САА 1 опираются на одну дугу, и поэтому равны.

Чтобы решить задачу:

• Во-первых, надо научиться анализировать условие задачи. Полезно придерживаться правила: пока не произведён полный, глубокий анализ задачи, не построена её схематическая запись(чертеж), не приступать к самому решению.
• Во-вторых, решение любой геометрической задачи есть последовательное применение каких-то знаний к условиям данной задачи, получение из этих условий следствий (промежуточных решений) до тех пор, пока не получены такие следствия, которые являются ответами на требования (вопросы) задачи. А для того, чтобы получать эти следствия, надо хорошо помнить все знания (определения, формулы, теоремы) из курса математики.
• В-третьих, надо уметь использовать основные методы решения задач.

Д.Пойа «Как решать задачу»

• https://kopilkaurokov.ru/matematika/prochee/formirovaniie-umieniia-rieshat-zadachi-po-ghieomietrii
• http://vschool.org.ru/images/doc/proekt/2016-17/math/proekt_math-9.pdf

Спасибо

за

внимание