Понятие дифференциального уравнения. Методы решения дифференциальных уравнений I и II порядков

Лекция: Понятие дифференциального уравнения.

Методы решения дифференциальных уравнений I и II порядков

Переходим к изучению последнего раздела математического анализа, связанного с решением дифференциальных уравнений. В дифференциальных уравнениях неизвестная функция содержится вместе со своими производными. Дифференциальные уравнения являются основой математических моделей, к построению которых приводит изучение закономерностей общественных процессов, исследование разнообразных явлений, происходящих в природе. В описания конкретных свойств систем и механизмов, в выражения тех или иных научных законов входят, как правило, производные интересующих функций, а не сами функции. Основной задачей теории дифференциальных уравнений является изучение функций, представляющих собой решения этих уравнений. Мы рассмотрим обыкновенные дифференциальные уравнения, в которых неизвестные функции зависят от одной переменной; познакомимся с некоторыми видами дифференциальных уравнений I и II порядков; методами их решения.

Определение: Дифференциальным уравнением (ДУ) называется уравнение, содержащее производные от искомой функции или ее дифференциалы.

Если в уравнение входит первая производная и не входят производные более высокого порядка, то уравнение называют ДУ I порядка. Если в уравнение входит вторая производная и не входят производные более высокого порядка, то уравнение называют ДУ II порядка.

В общем случае ДУ I порядка можно записать следующим образом: 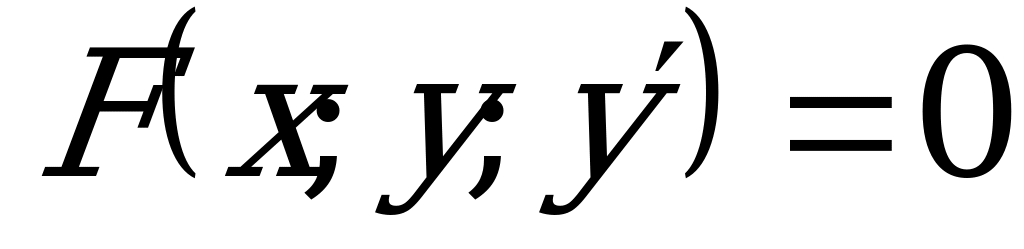, где 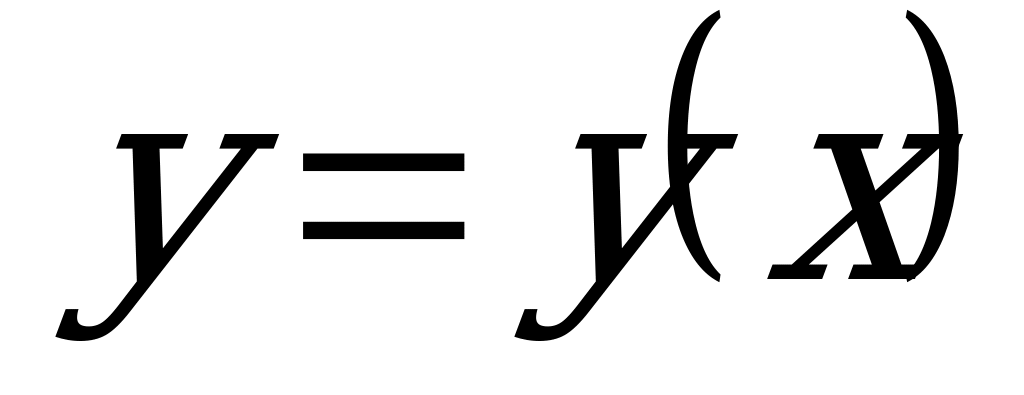- искомая неизвестная функция;

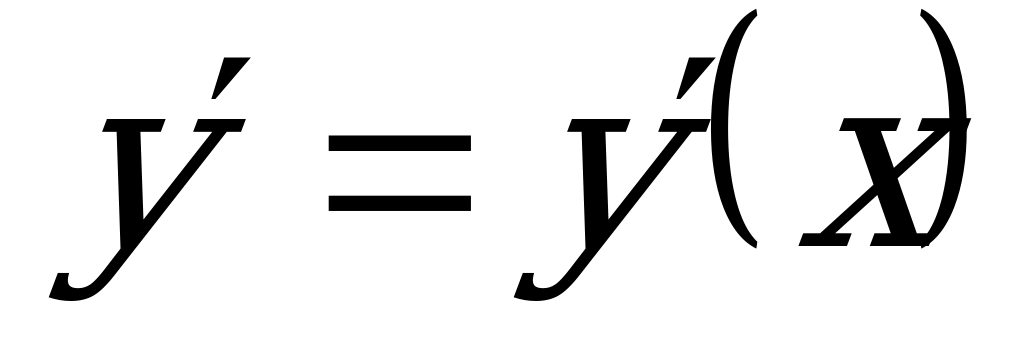- ее производная;

- заданная функция переменных .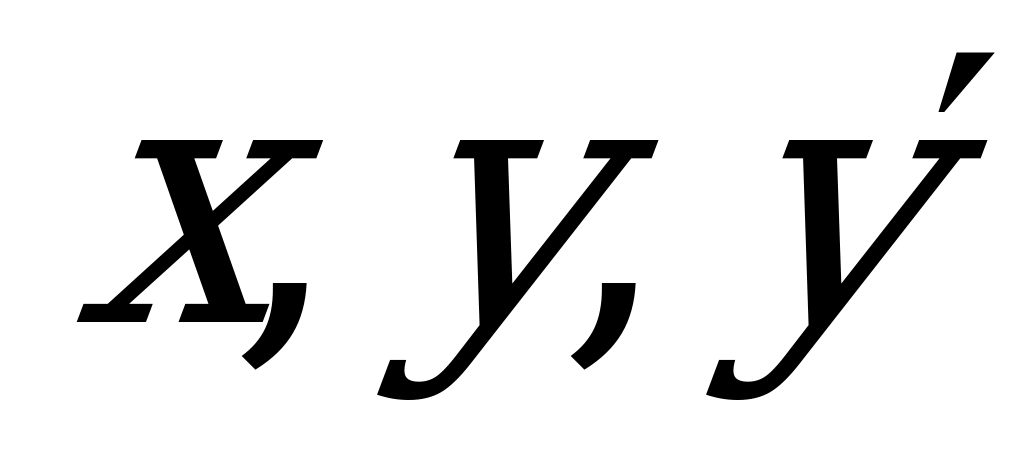

Обычно ДУ записывают в явном виде: .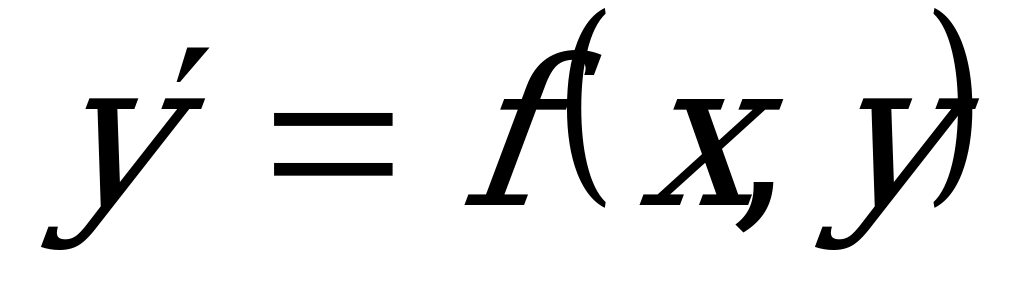

Примеры ДУ I порядка:

1) 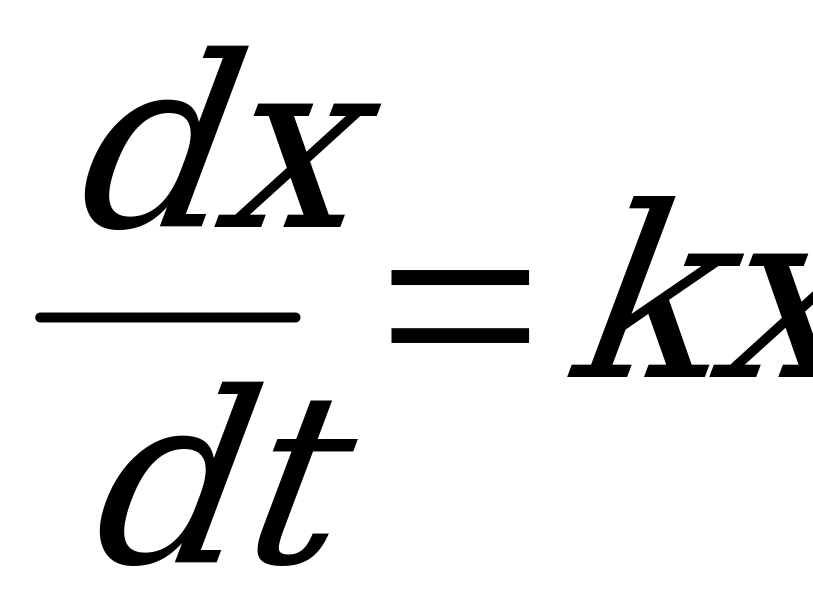- уравнение размножения бактерий.

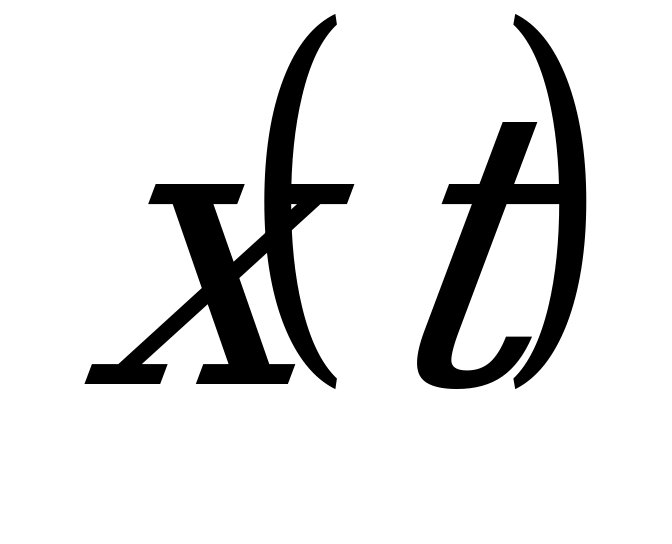- масса бактерий;

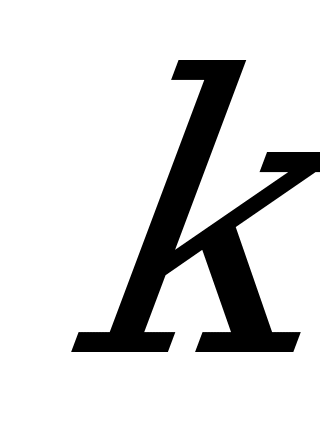- коэффициент размножения.

2) 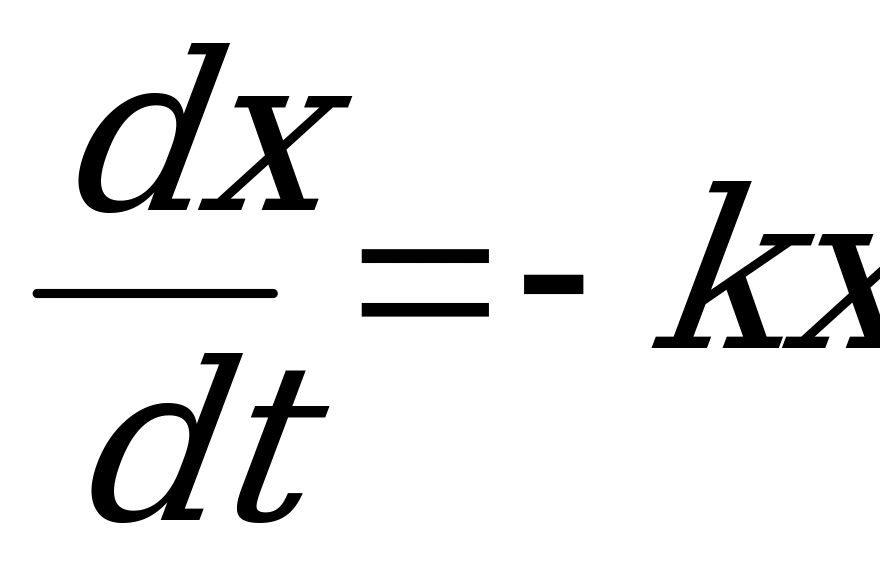- уравнение радиоактивного распада.

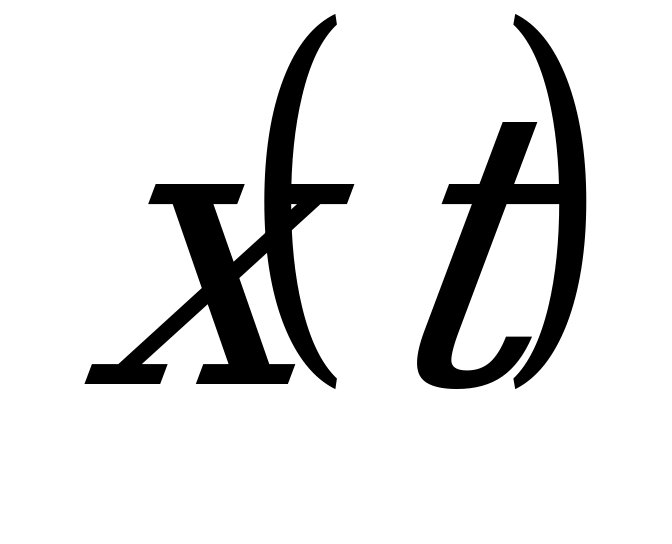- масса нераспавшегося вещества;

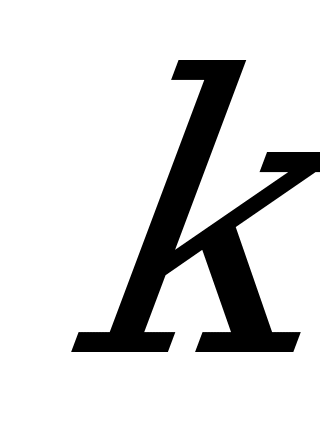- const, зависящая от периода полураспада радиоактивного вещества.

Определение: Решением ДУ называется некоторая функция 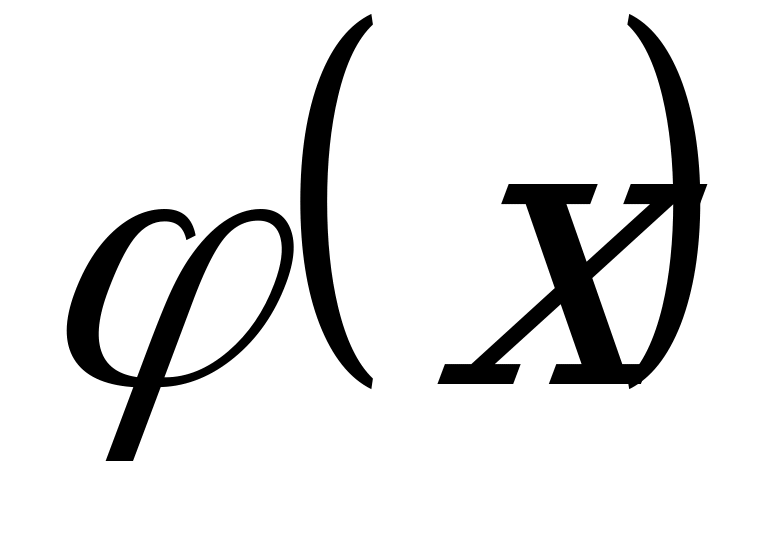, которая удовлетворяет заданному уравнению, т. е. обращает уравнение в тождество.

Например, решением уравнения размножения бактерий является .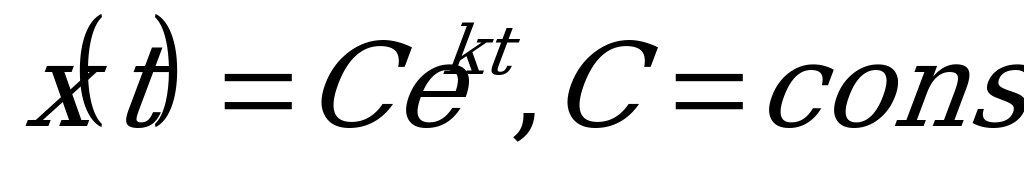

Определение: Функция, являющаяся решением ДУ и содержащая произвольную постоянную называется общим решением уравнения.

Выше приведено общее решений уравнения размножения бактерий.

Определение: Решение ДУ, удовлетворяющее заданным начальным условиям называется частным решением ДУ или решением задачи Коши.

Методы решения ДУ зависят от вида уравнений. Рассмотрим несколько видов ДУ I и II порядков.

1. Дифференциальные уравнения с разделяющимися переменными.

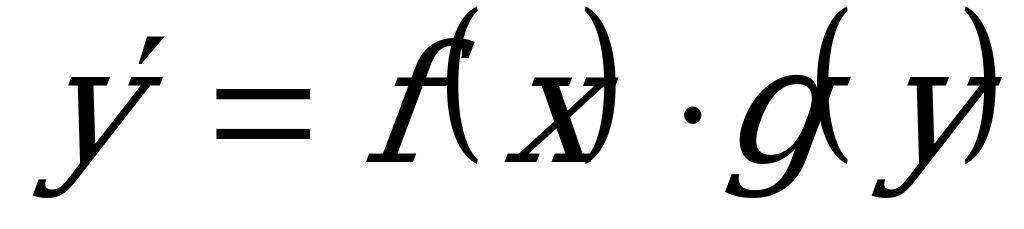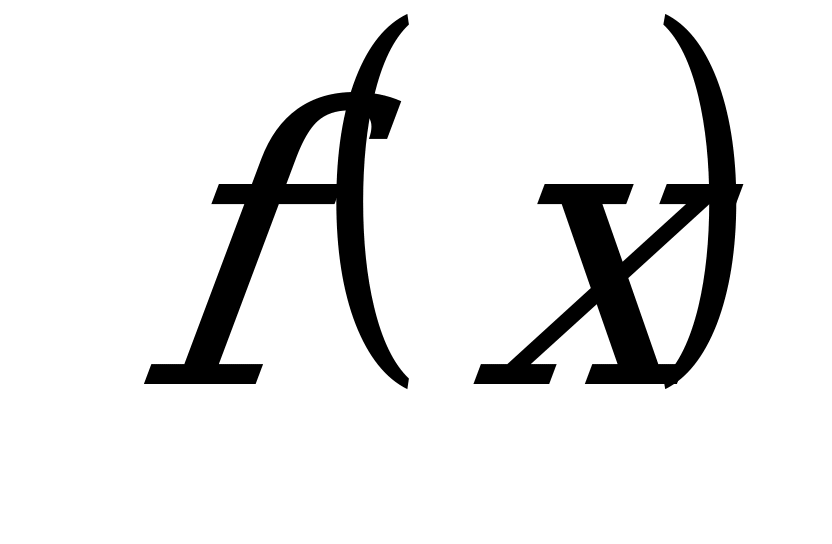Определение: ДУ вида , где и 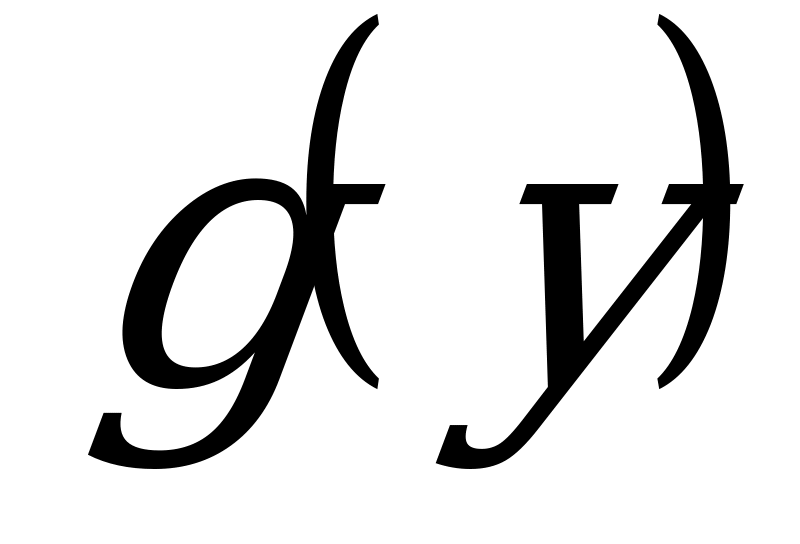- заданные функции, называется ДУ с разделяющимися переменными.

Алгоритм решения ДУ с разделяющимися переменными:

1) Разделяем переменные, т. е. преобразуем ДУ к виду: .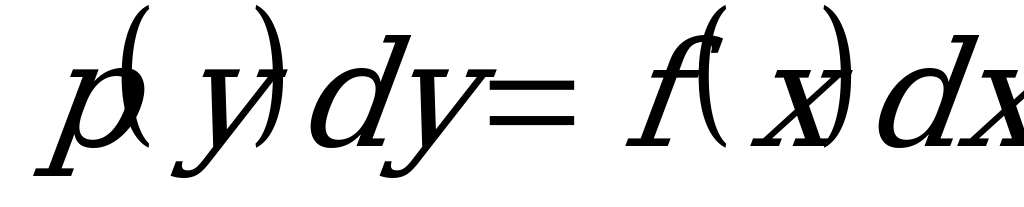

2) Интегрируем обе части ДУ по у и х соответственно (левую часть по у, правую - по х) и записываем уравнение в виде: .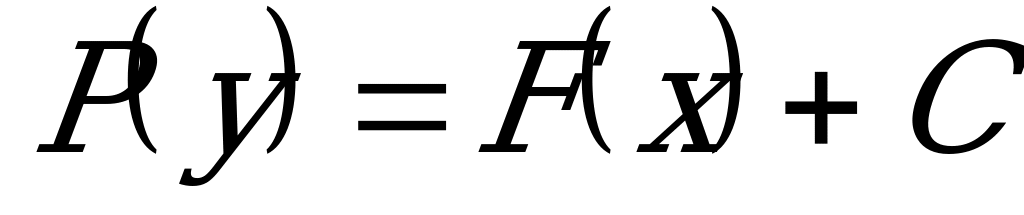

3) Выразив у, получаем общее решение ДУ .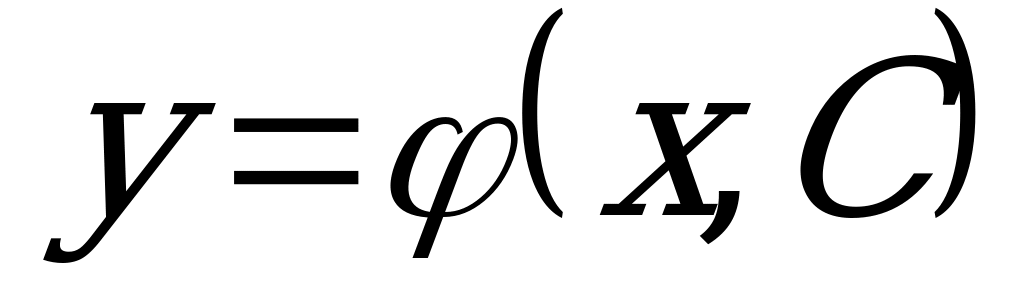

4) Находим частное решение уравнения, используя начальные условия.

Пример 1. Решить уравнение: .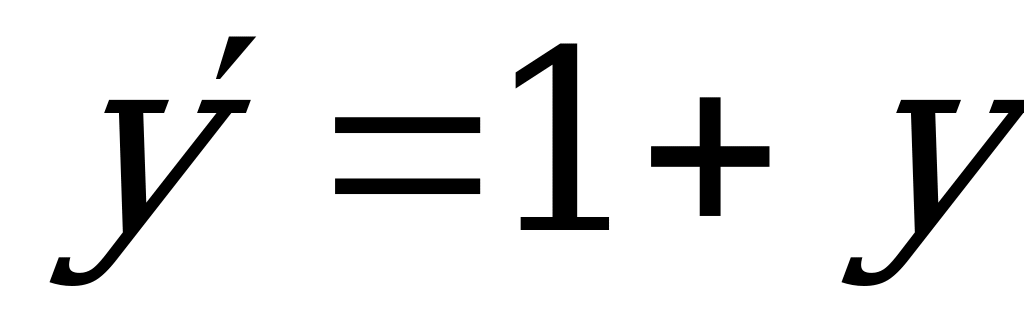

Решение:

Под решение уравнения подразумевается нахождение его общего решения. Если надо найти частное решение уравнения, это указывается в задании. В данном случае, нам необходимо найти общее решение уравнения, т. е. выполнить первые три пункта предложенного алгоритма.

1) Распишем производную через дифференциалы 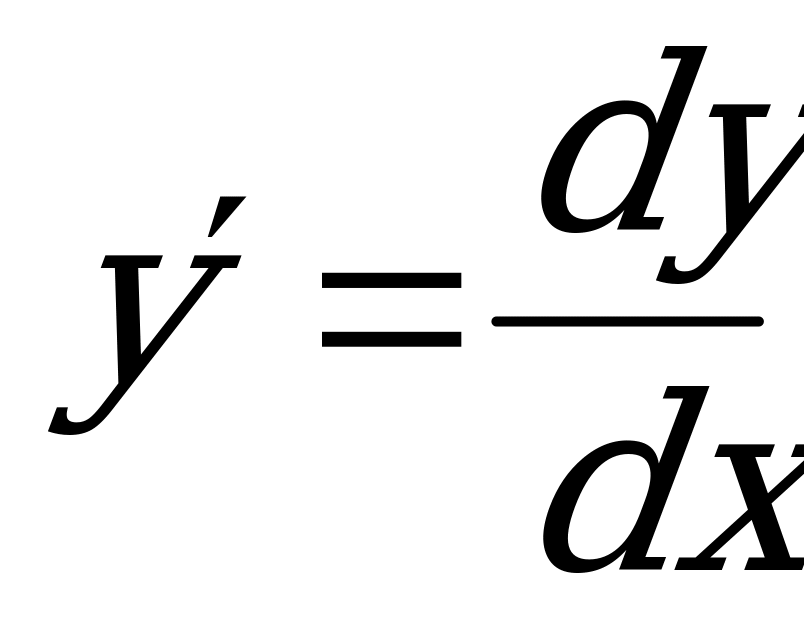и запишем уравнение в виде: .

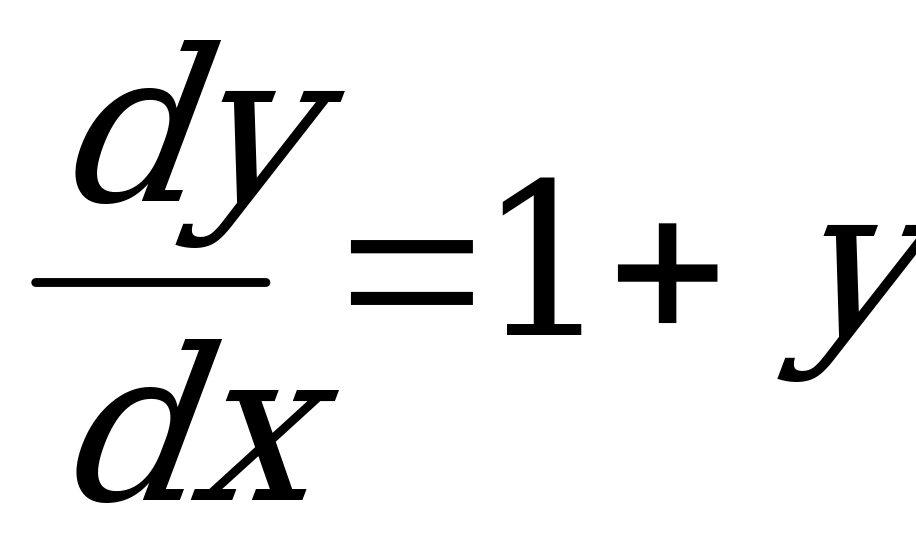Разделим переменные, для этого обе части уравнения умножим на произведение : .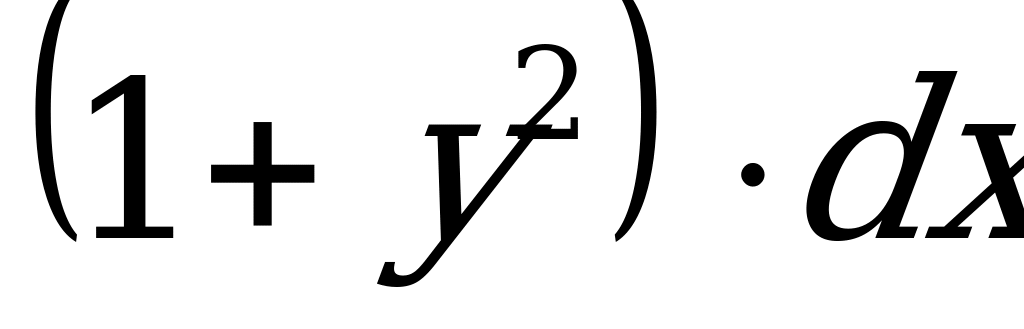

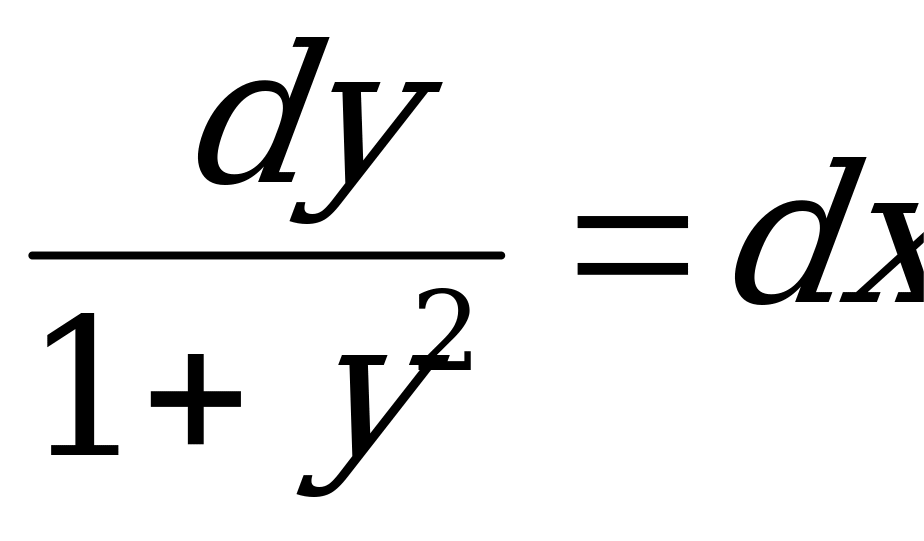2) Проинтегрируем обе части ДУ по у и х соответственно:

.

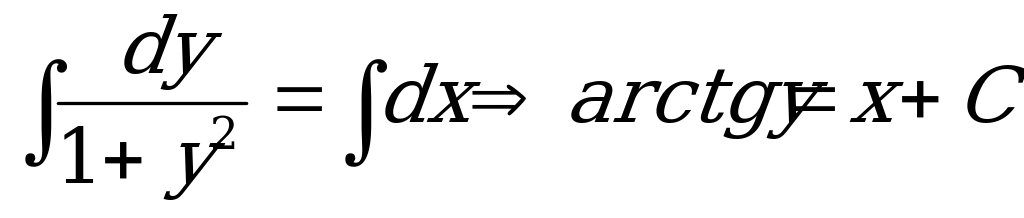3) Выразим у явно, получим общее решение ДУ: .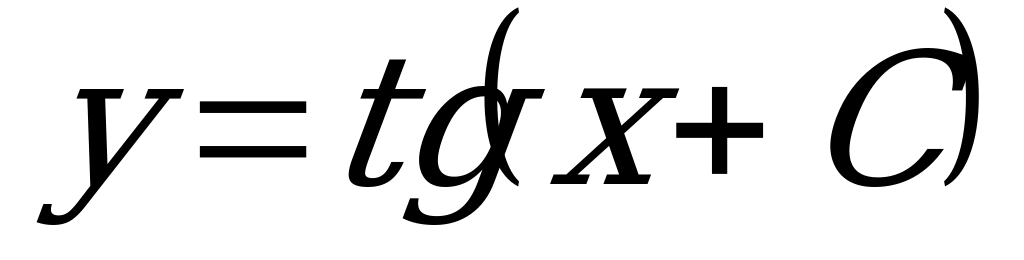

Ответ: .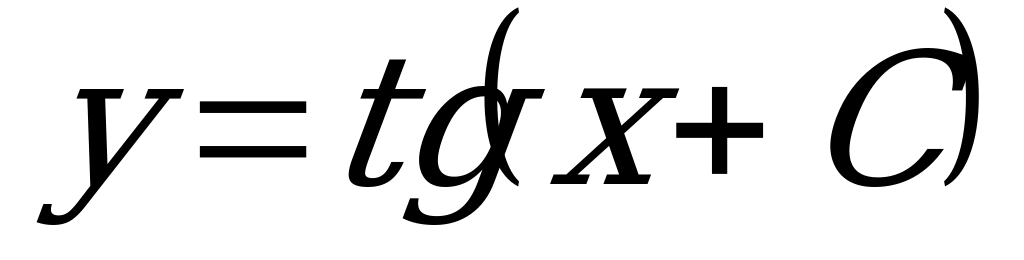

Пример 2. Решить уравнение: .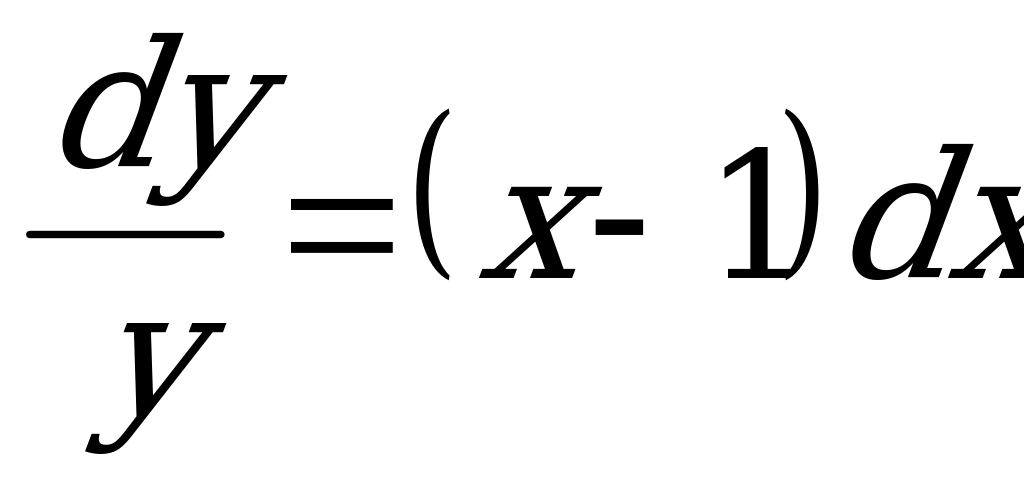

Решение:

1) Уравнение записано через дифференциалы. Переменные разделены.

2) Проинтегрируем обе части ДУ по у и х соответственно:

.

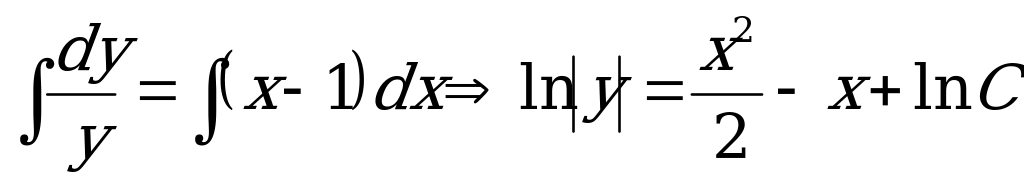Обратите внимание, при решении данного уравнения вместо постоянной интегрирования С записан ее логарифм! Так делают в том случае, если в решении содержится логарифм.

3) Используя определение и свойства логарифма, выразим у явно:

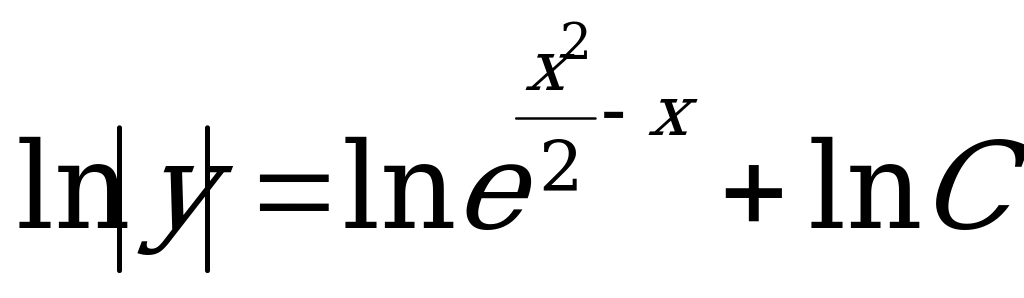
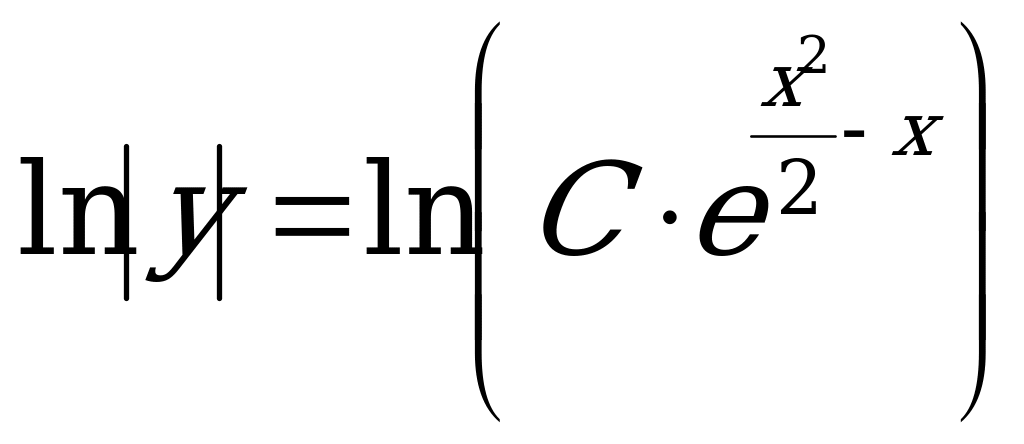
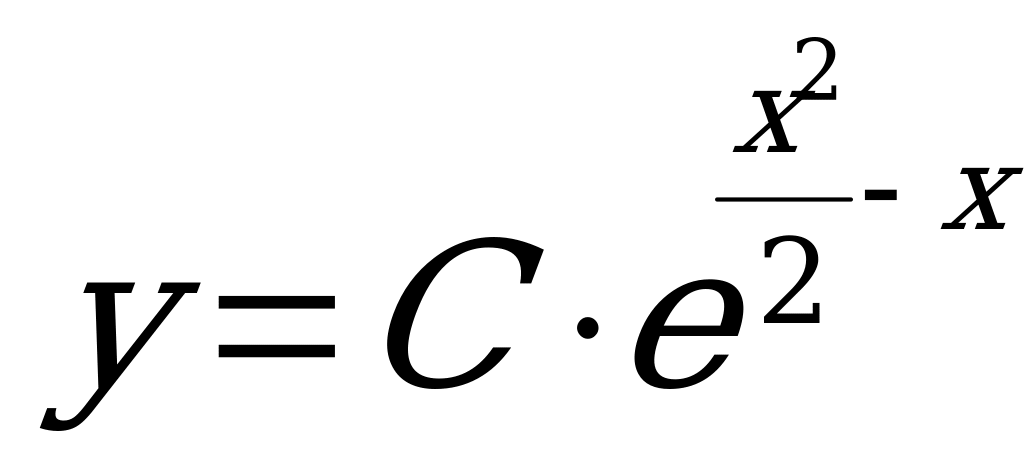- общее решение уравнения.

Ответ: .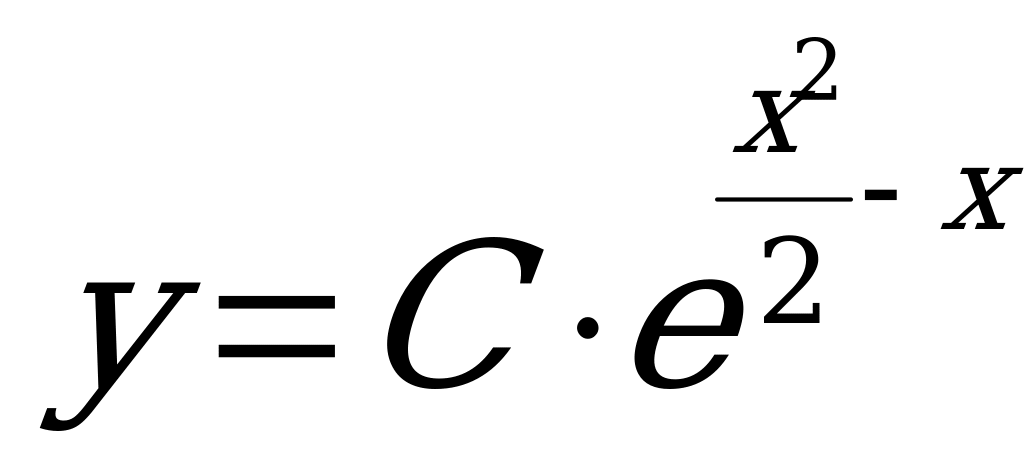

Пример 3. Найти частное решение ДУ 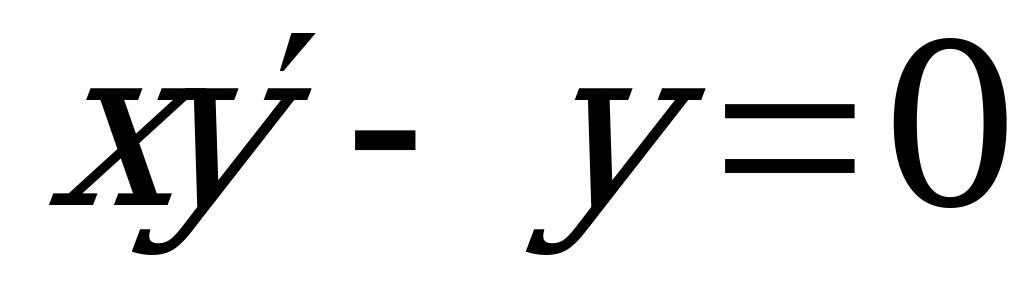при начальных условиях .

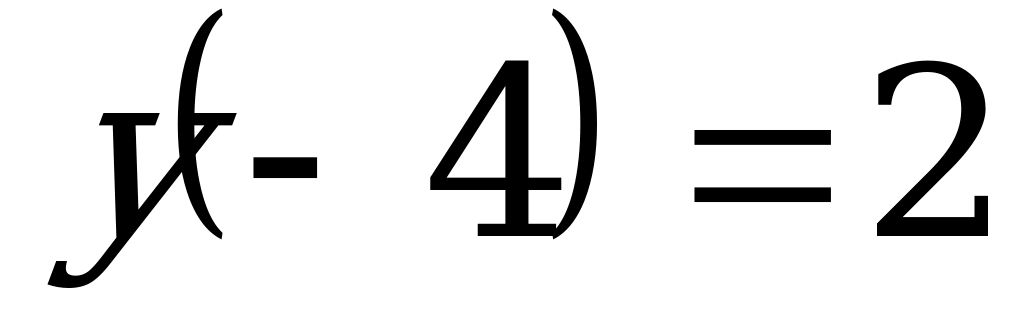Решение:

1) Разделим переменные, записав предварительно, что :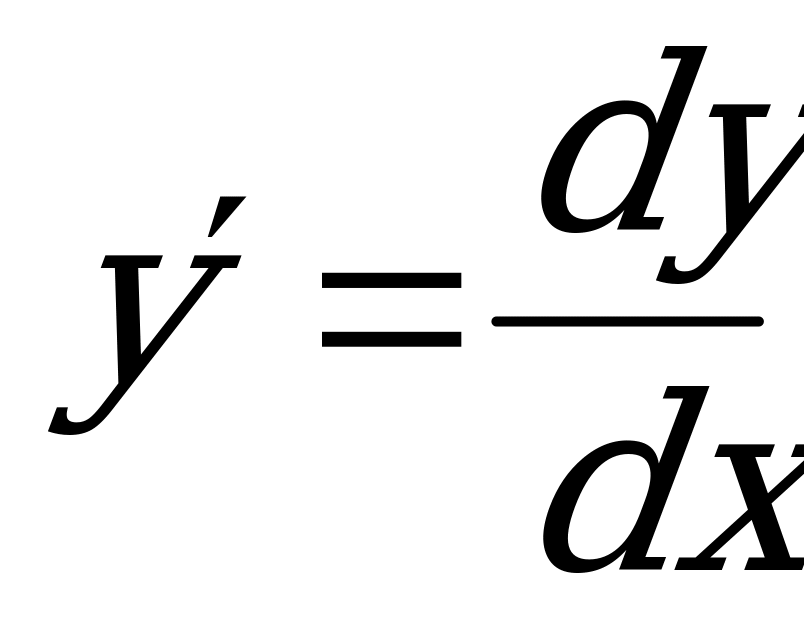

.

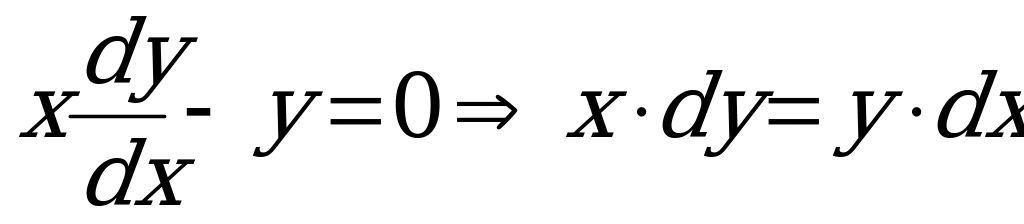Разделим обе части на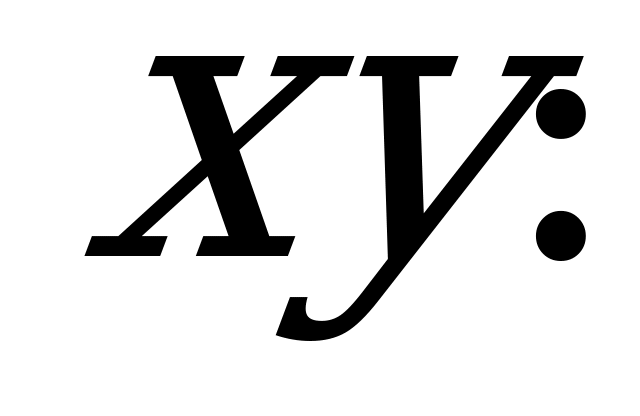

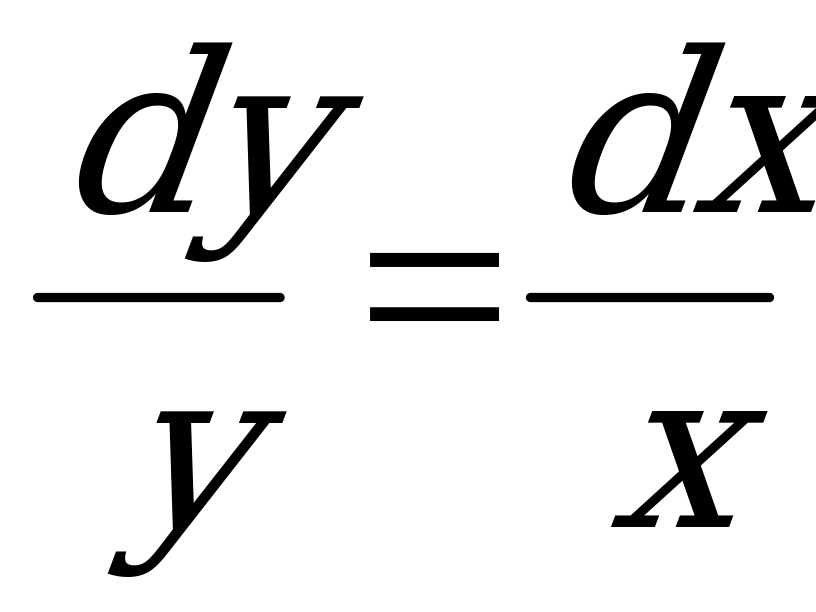
2) Проинтегрируем обе части ДУ по у и х соответственно:

.

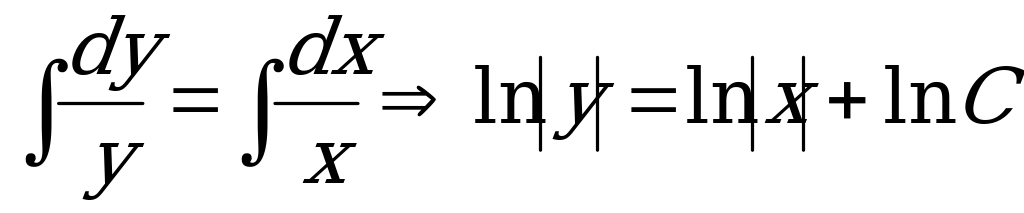3) Выразим у явно:

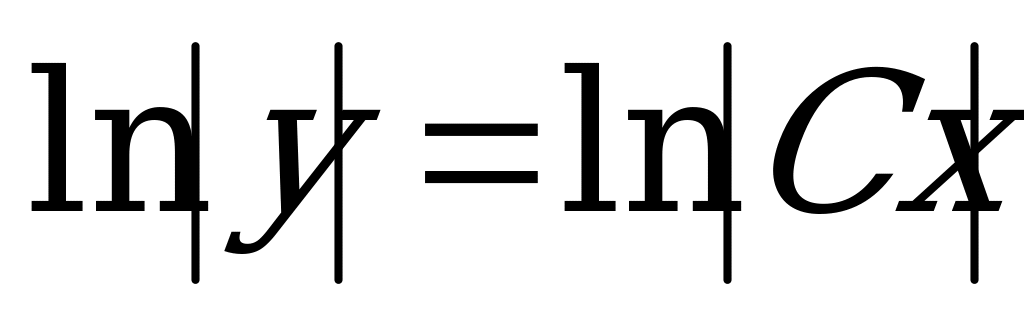
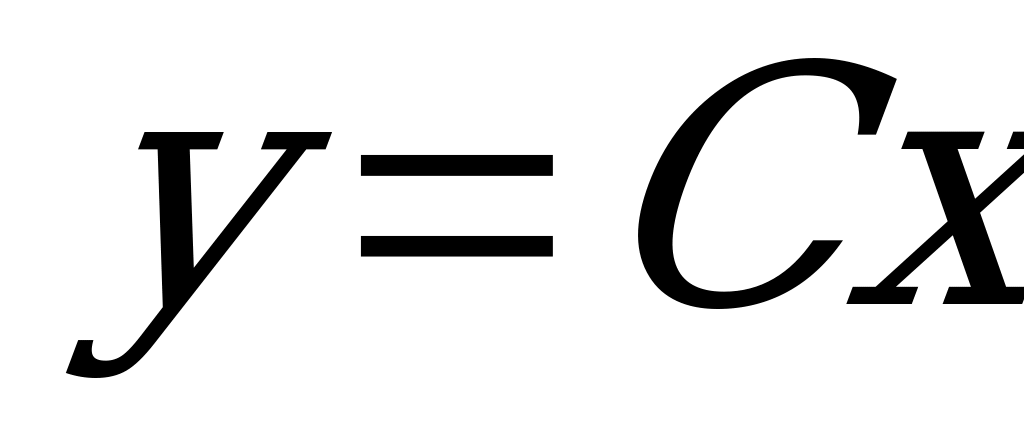- общее решение уравнения.

4) Найдем частное решение уравнения. В общее решение уравнения вместо х и у подставим начальные данные и найдем значение произвольной постоянной С.

.

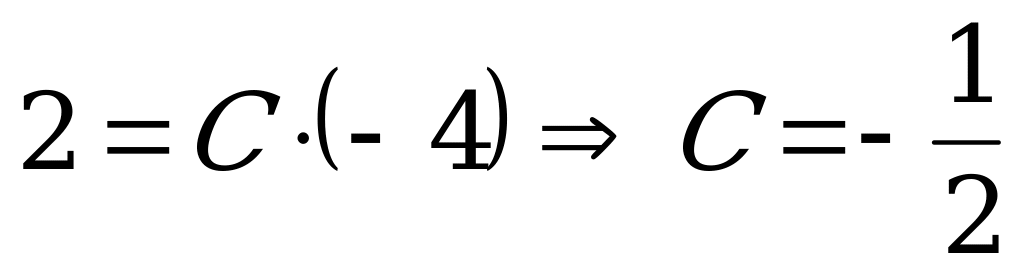Следовательно, частное решение имеет вид: .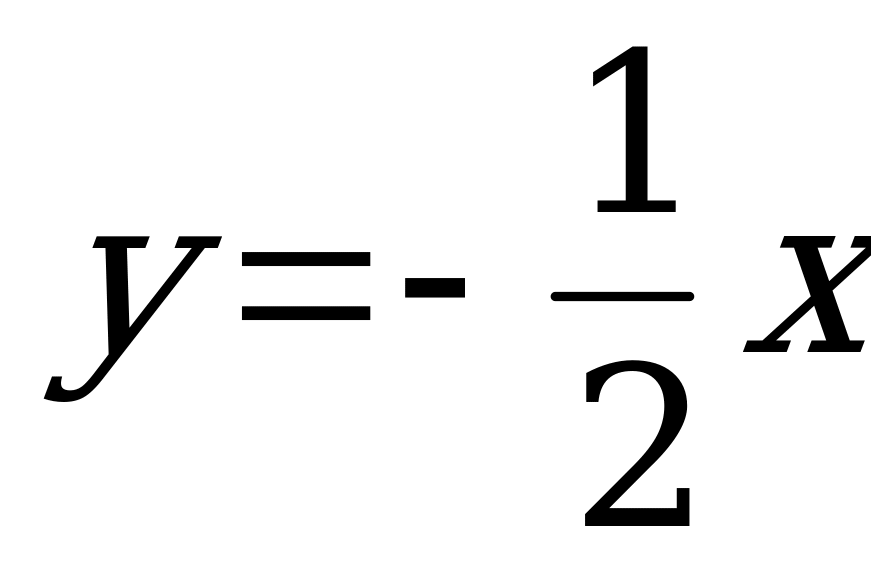

Ответ: . .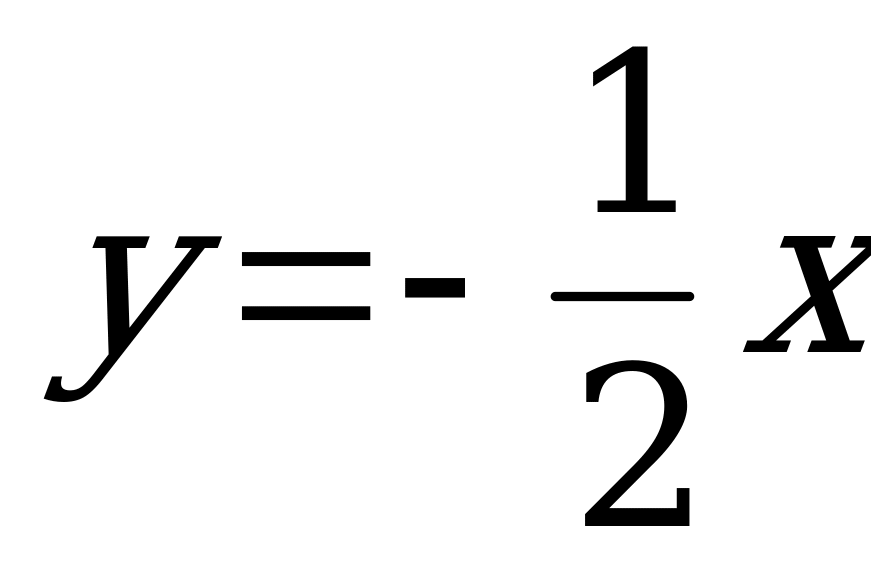

2. Линейные дифференциальные уравнения первого порядка.

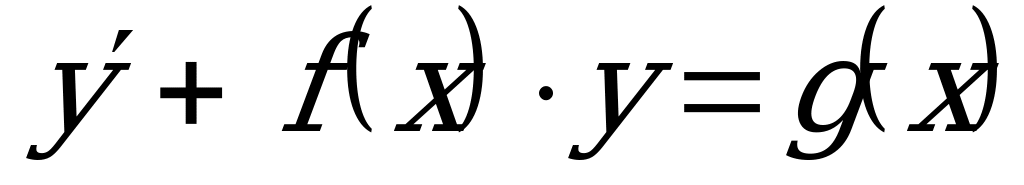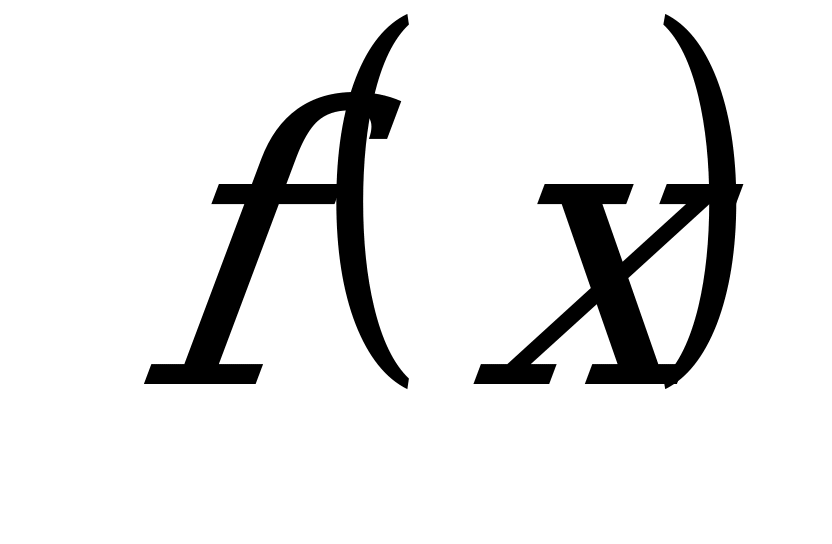Определение: ДУ вида , где и 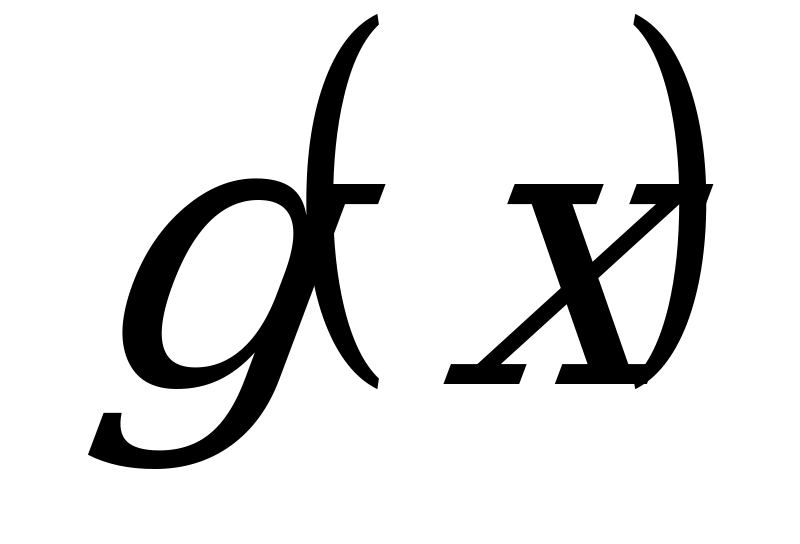- заданные функции, называется линейным ДУ I порядка.

Если 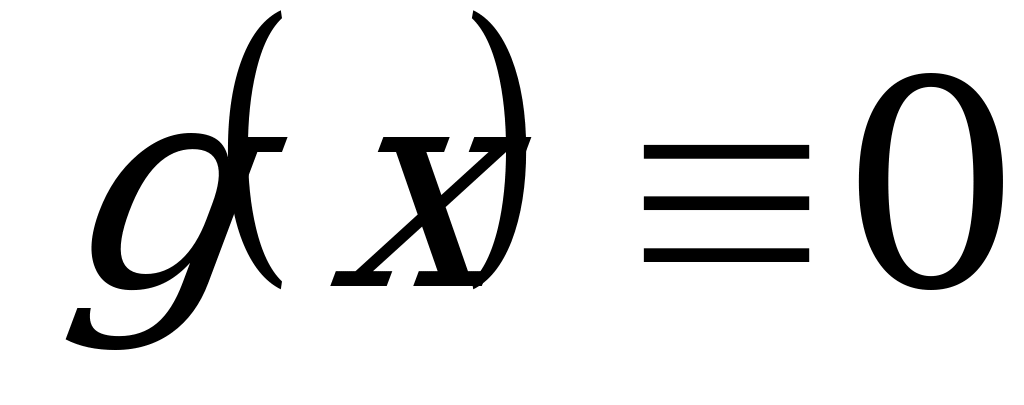, то уравнение имеет вид 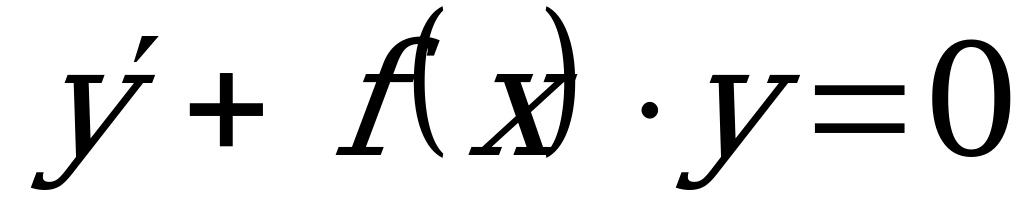и называется однородным линейным ДУ I порядка. Решением этого уравнения является функция: .

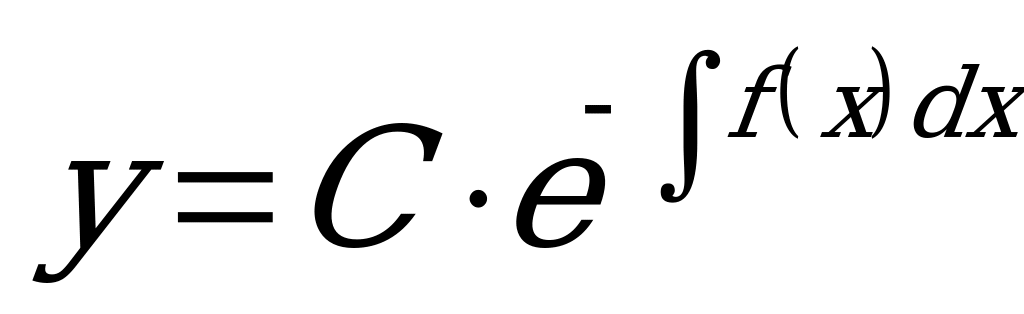Если 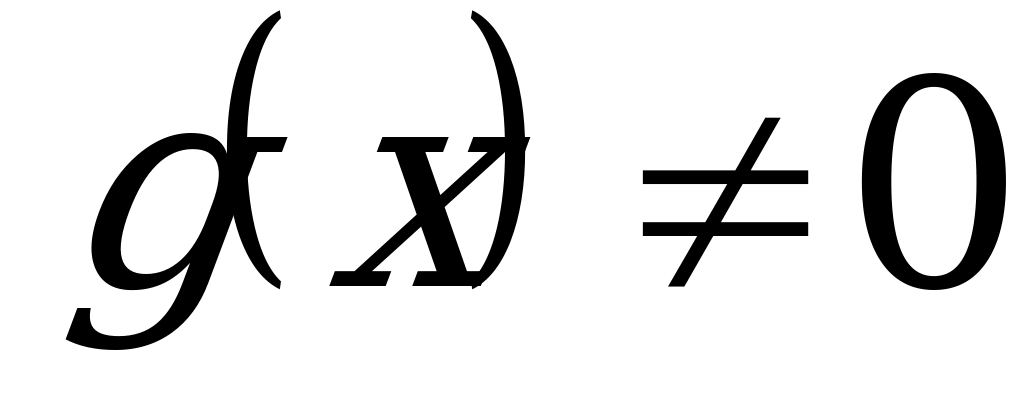, то уравнение называется неоднородным линейным ДУ I порядка. Общее решение неоднородного линейного ДУ находится методом вариации произвольной постоянной и имеет вид: .

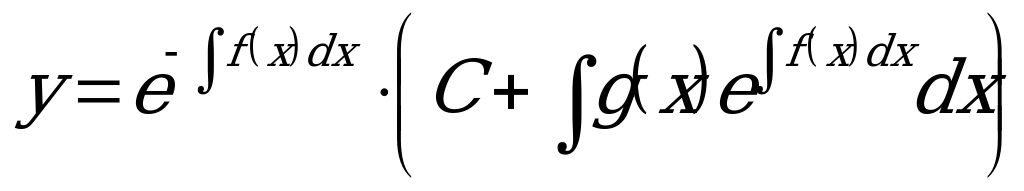Алгоритм решения линейного ДУ I порядка:

1) Определяем вид линейного ДУ I порядка (однородное или неоднородное). Выписываем функци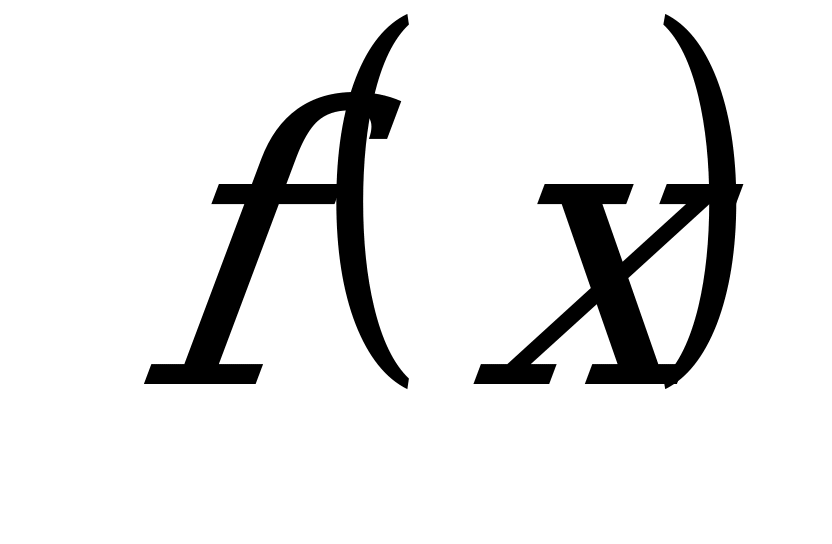и и .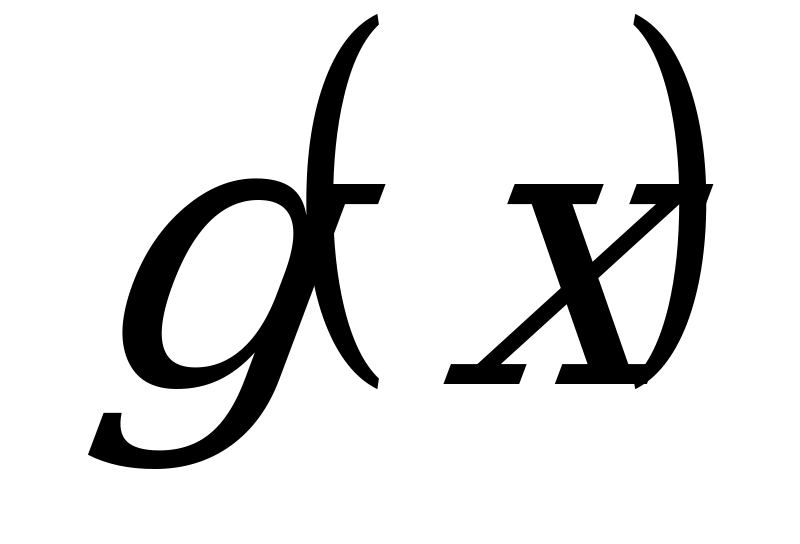

2) Вычисляем необходимые интегралы и записываем общее решение линейного уравнения: 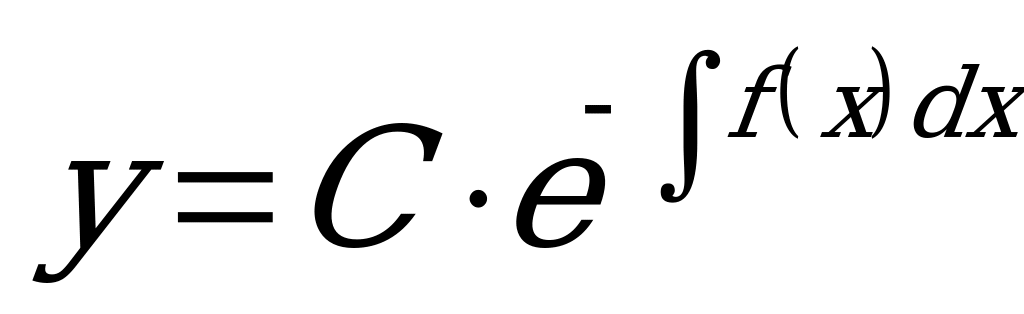(для однородного уравнения) и 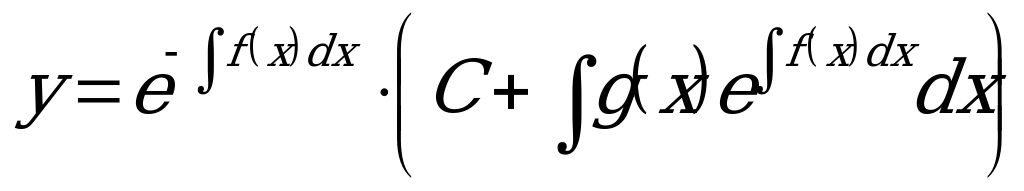(для неоднородного).

3) Находим частное решение уравнения, используя начальные условия.

Пример 3. Решить уравнение: .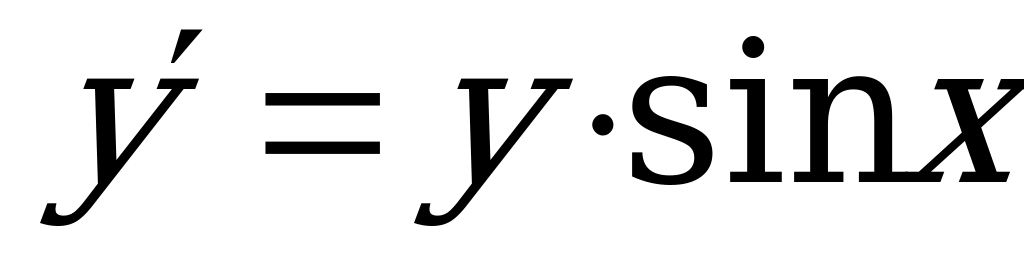

Решение:

1) Перепишем уравнение в виде: .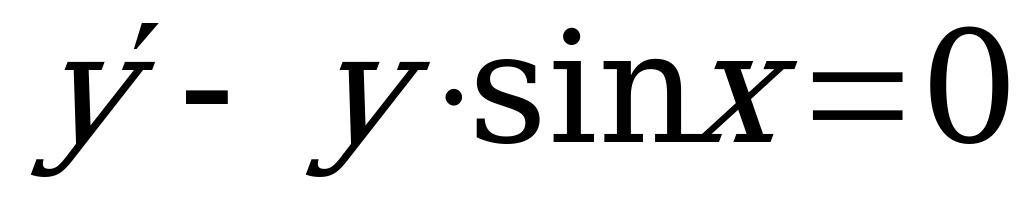

; .

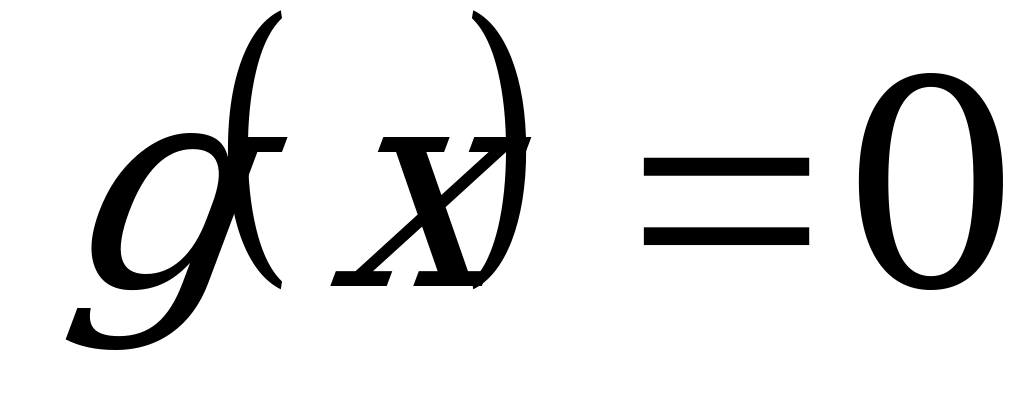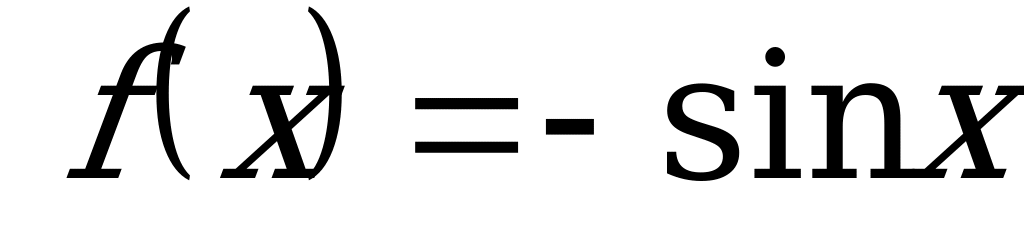Так как 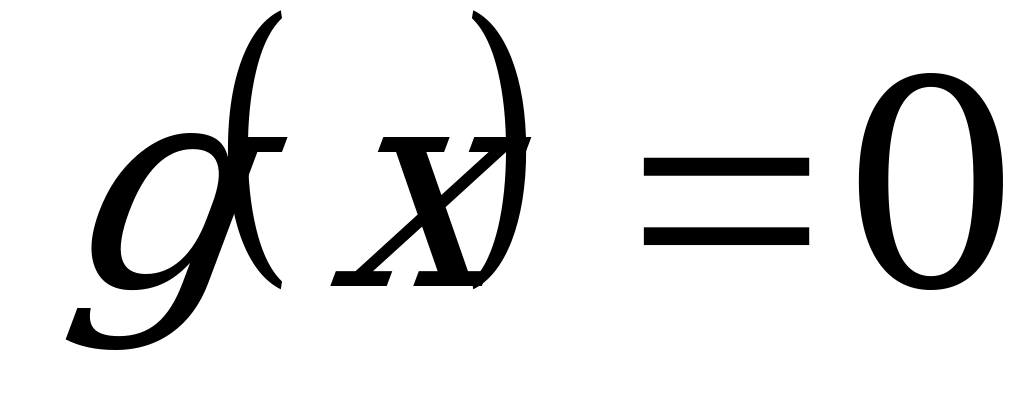, то уравнение является однородным.

2) Общее решение однородного линейного уравнения имеет вид: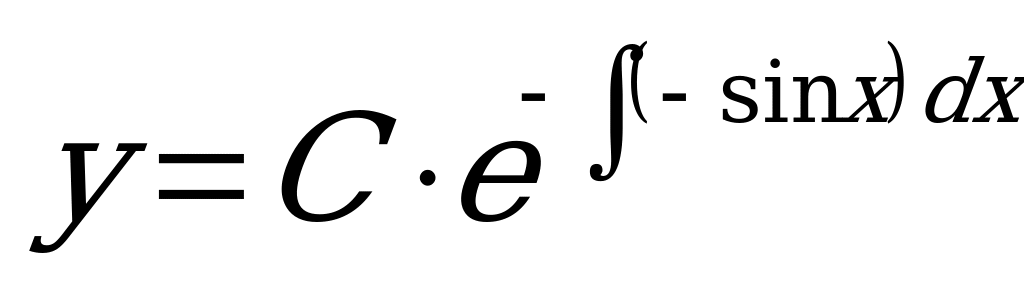

.

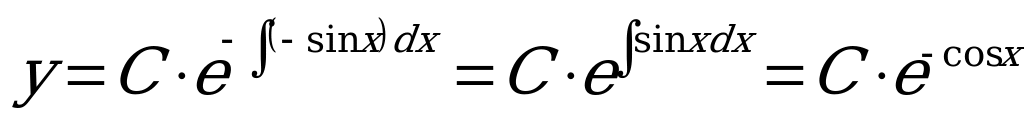Ответ: .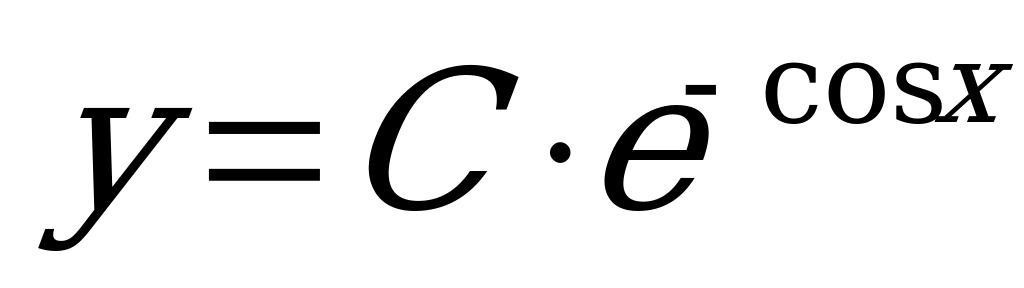

Пример 4. Решить уравнение: .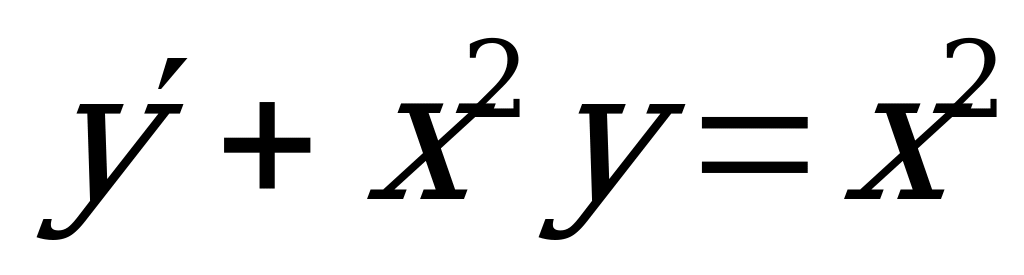

Решение:

1) ; .

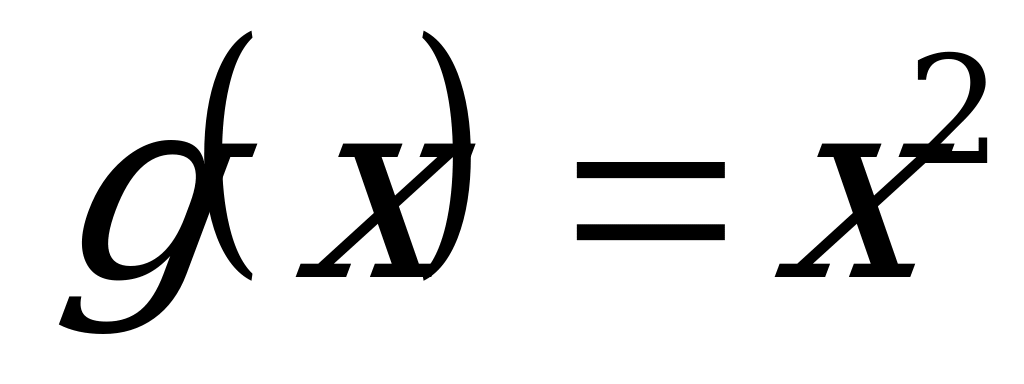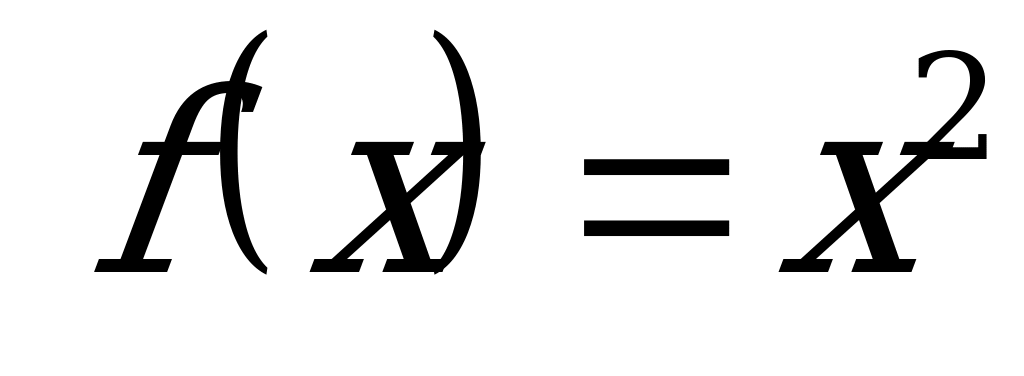Так как 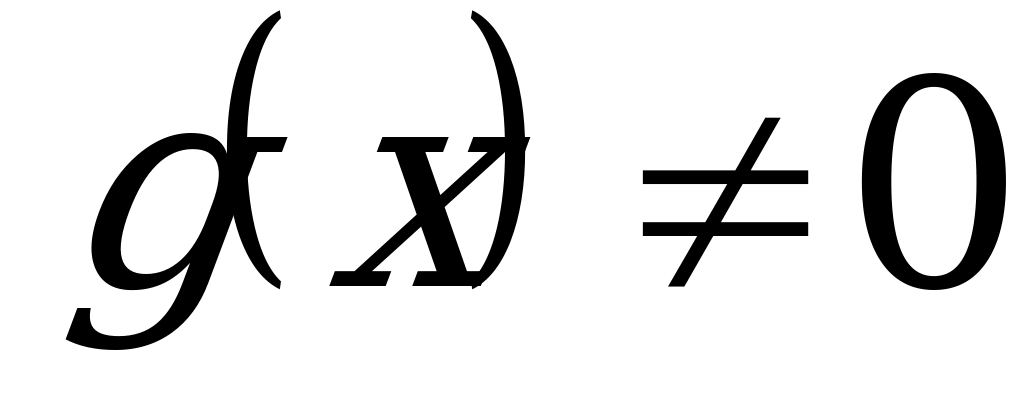, то уравнение является неоднородным.

2) Общее решение неоднородного линейного уравнения имеет вид:

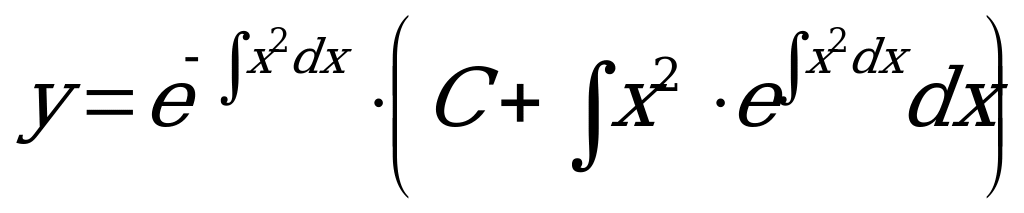
Вычислим необходимые интегралы 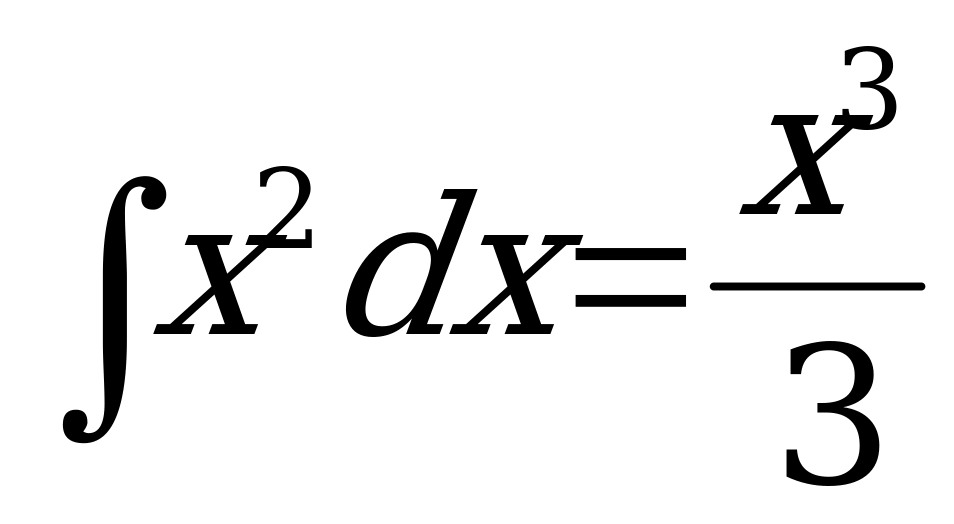; 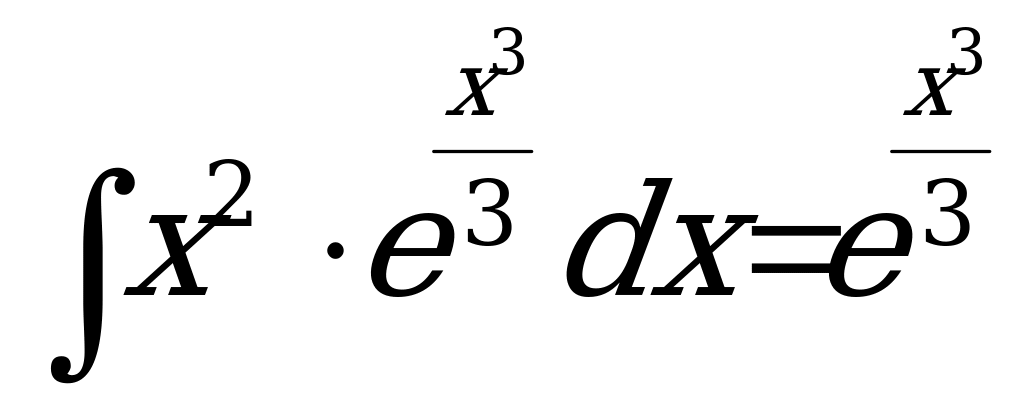. При вычислении интегралов полагаем С=0, поскольку постоянная интегрирования уже включена в общий вид решения.

Запишем общее решение ДУ: .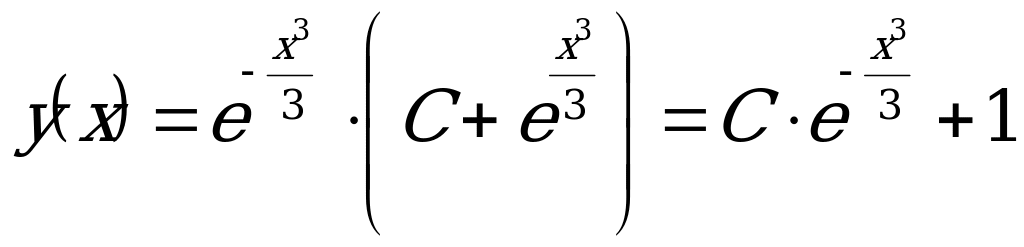

Ответ: .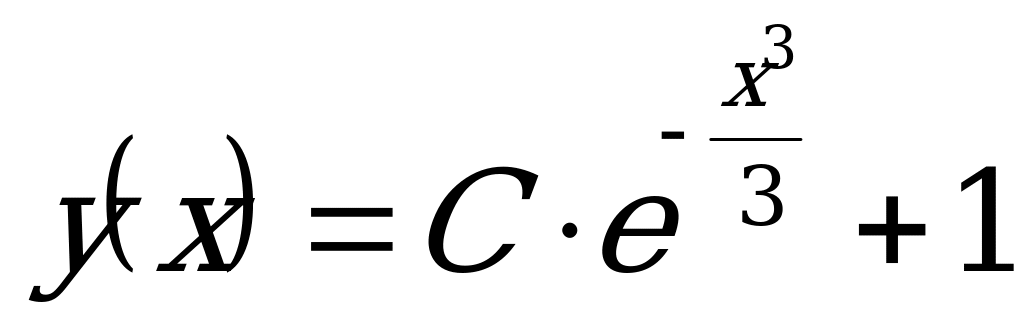

Примечание: Некоторые линейные ДУ I порядка являются частным случаем ДУ с разделяющимися переменными и для их решения можно применять алгоритм решения ДУ с разделяющимися переменными.

3. Дифференциальные уравнения второго порядка, допускающие понижение степени.

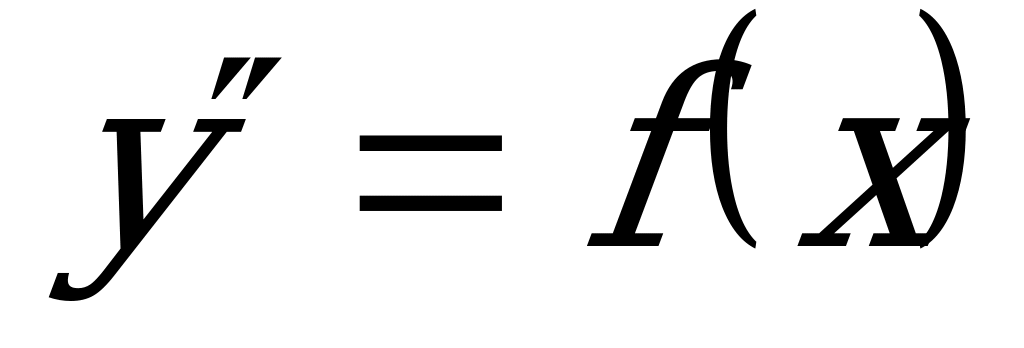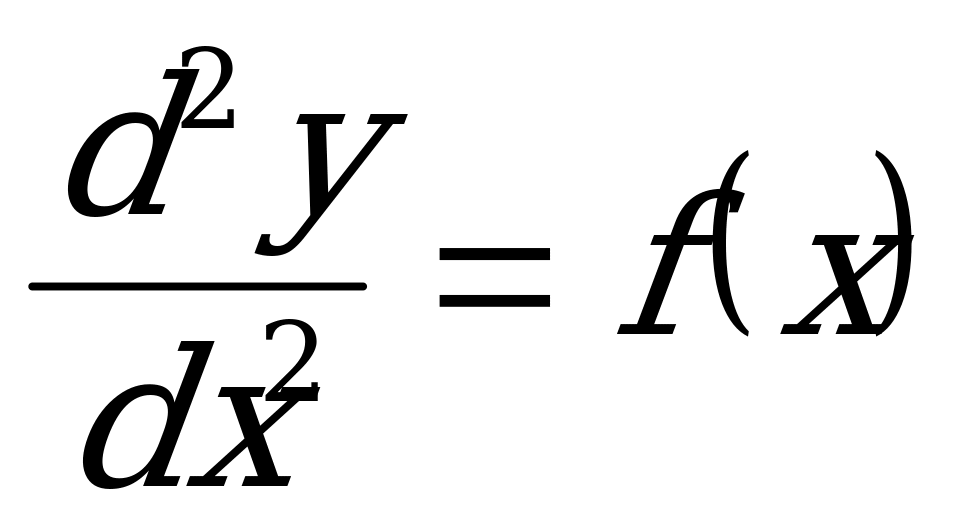Определение: Простейшим ДУ II порядка, допускающим понижение степени является уравнение вида или , где 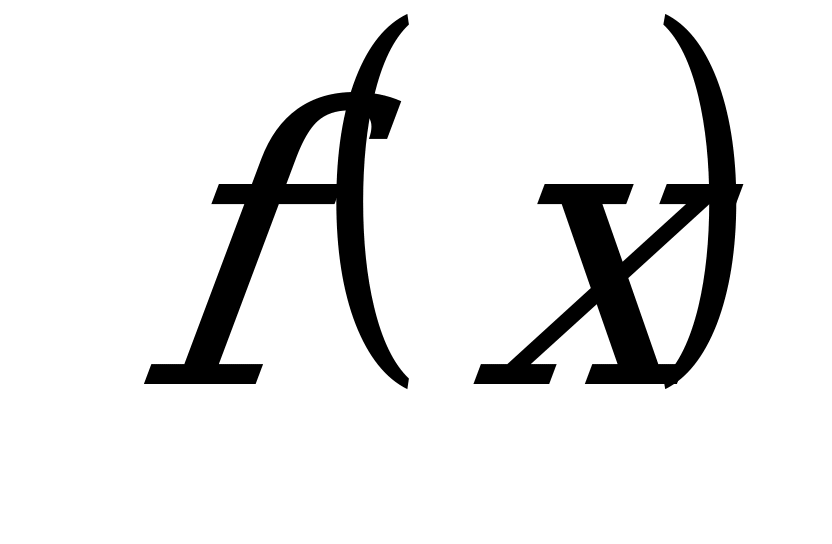заданная функция.

Данное уравнение решается двукратным интегрированием.

Алгоритм решения ДУ II порядка, допускающего понижение степени:

1) Вводим новую переменную .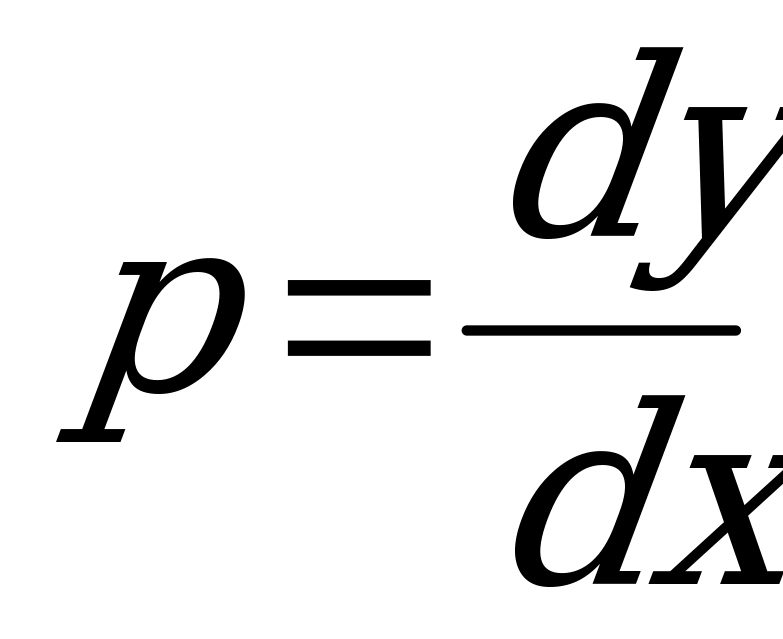

2) Переходим к ДУ I порядка относительно новой переменной и решаем полученное уравнение с разделяющимися переменными.

3) Возвращаемся к старой переменной и решаем полученное ДУ I порядка.

4) Находим частное решение уравнения, используя начальные условия.

Пример 5. Решить уравнение: .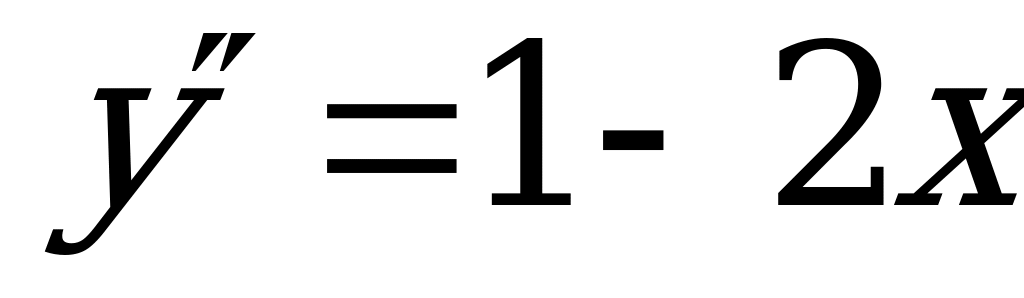

Решение:

1) Введем новую переменную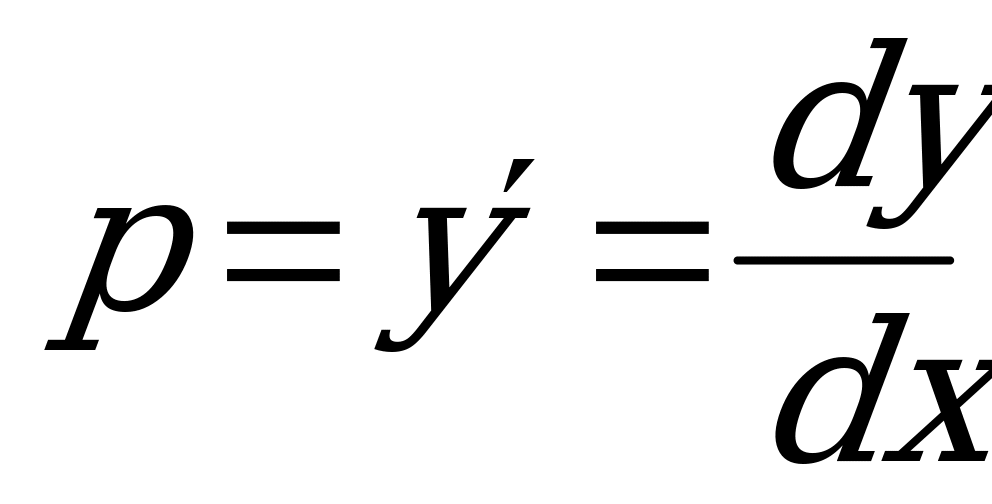

2) Получим уравнение I порядка с разделяющимися переменными: .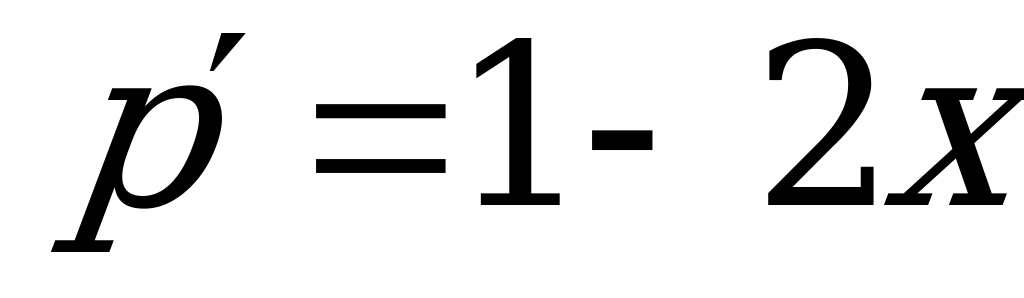

Перепишем уравнение в виде: .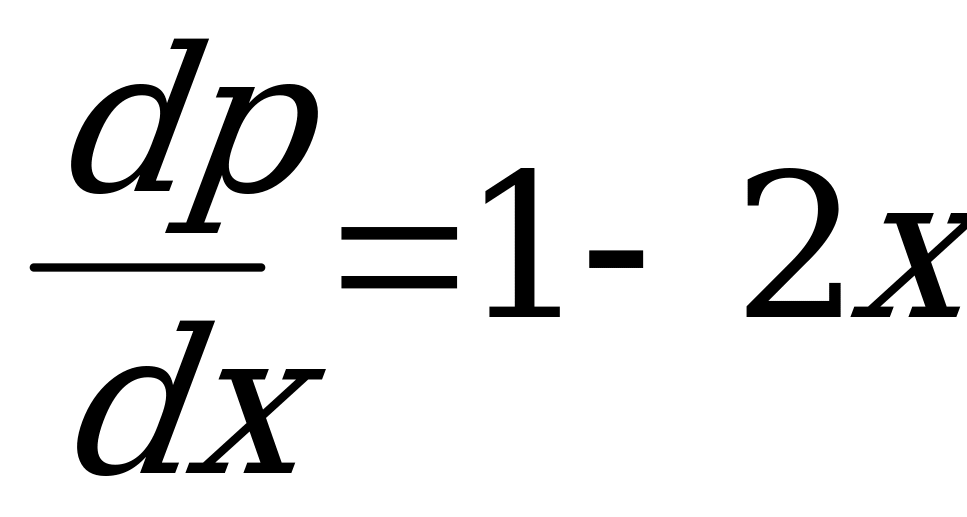

Разделим переменные : .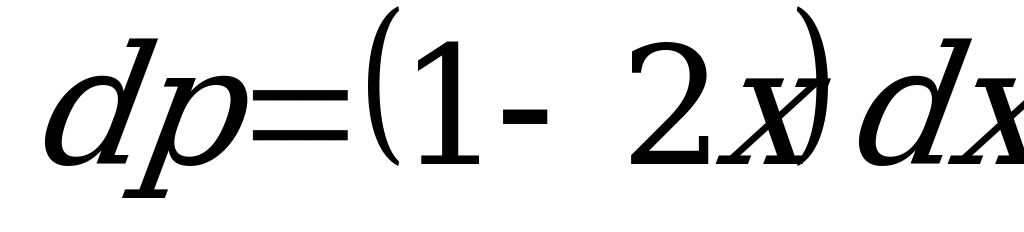

Проинтегрируем обе части полученного уравнения: .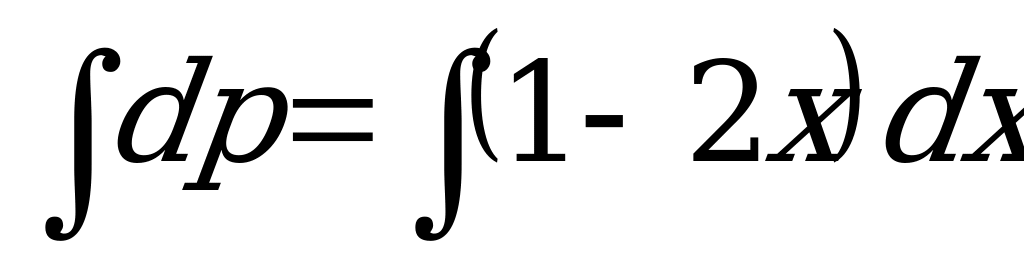

Получим .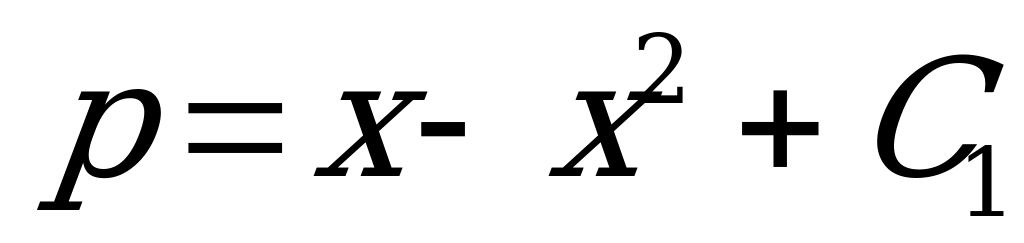

3) Вернемся к старой переменной и решим полученное уравнение: .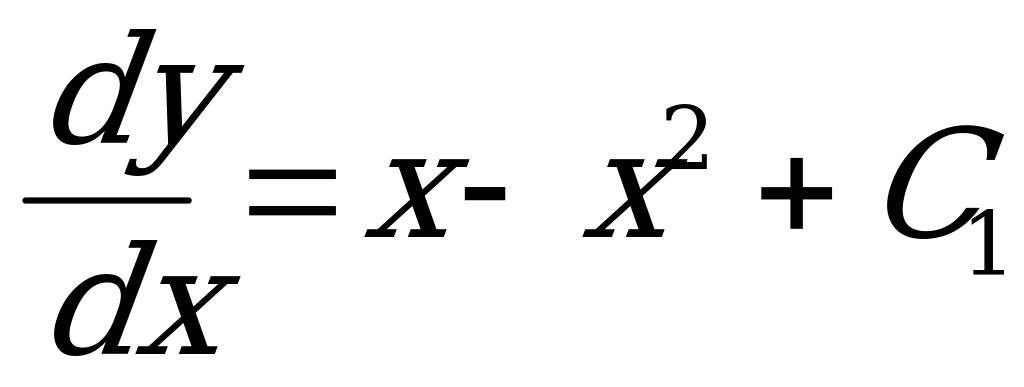

;

.

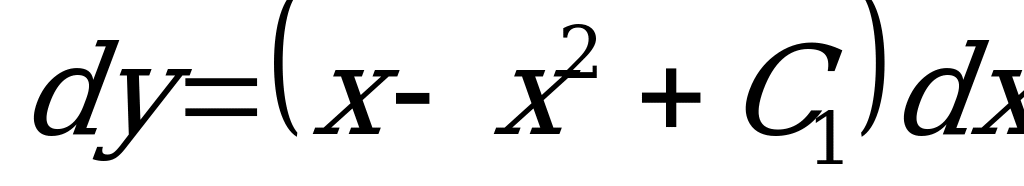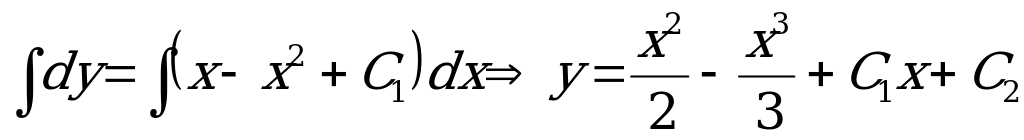Ответ: .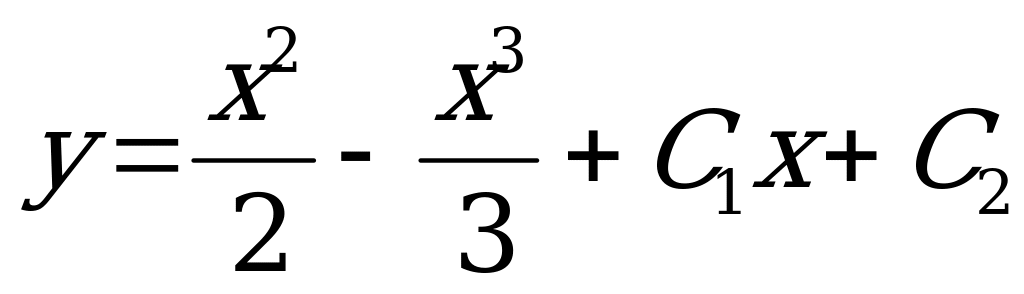

Примечание: Обратите внимание на то, что в общем решении ДУ II порядка присутствуют две постоянные интегрирования, поскольку интегрировать выражение приходится дважды.

4. Однородные линейные дифференциальные уравнения второго порядка.

Определение: ДУ вида 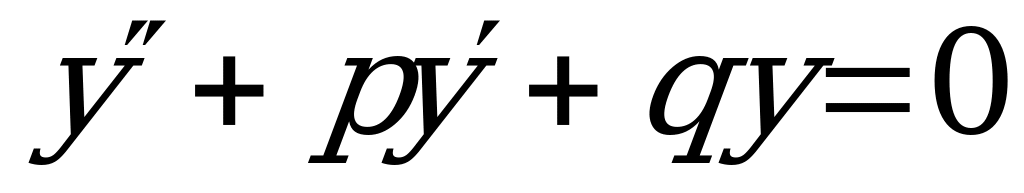, где 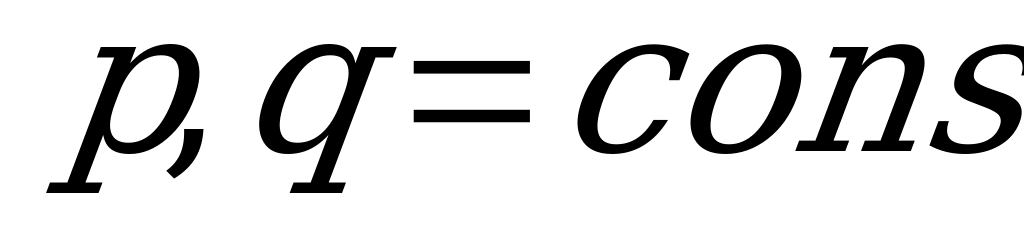называется однородным линейным ДУ II порядка с постоянными коэффициентами.

Для решения уравнения данного вида используют характеристическое уравнение, которое получают из исходного с помощью замены: : .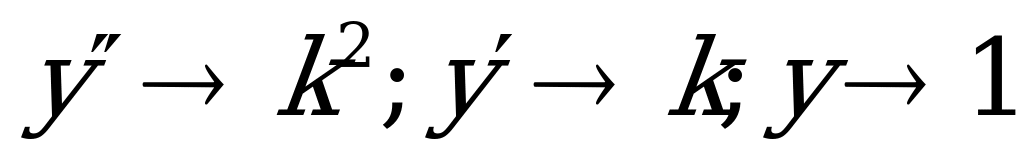

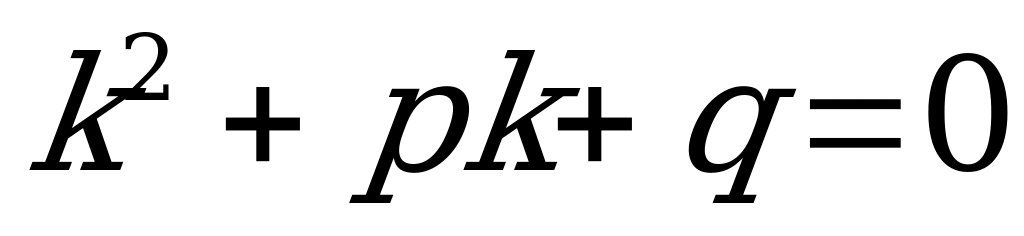Алгоритм решения однородного ДУ II порядка:

1) Составляем характеристическое уравнение: .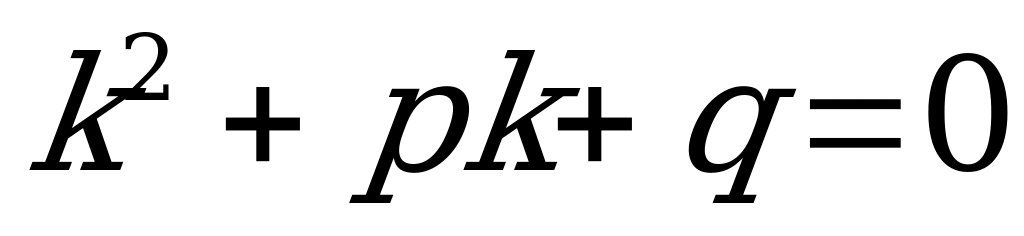

2) Решаем полученное квадратное уравнение.

В зависимости от знака дискриминанта, общее решение ДУ записывается по разному:

а) Если , то характеристическое уравнение имеет два действительных корня: 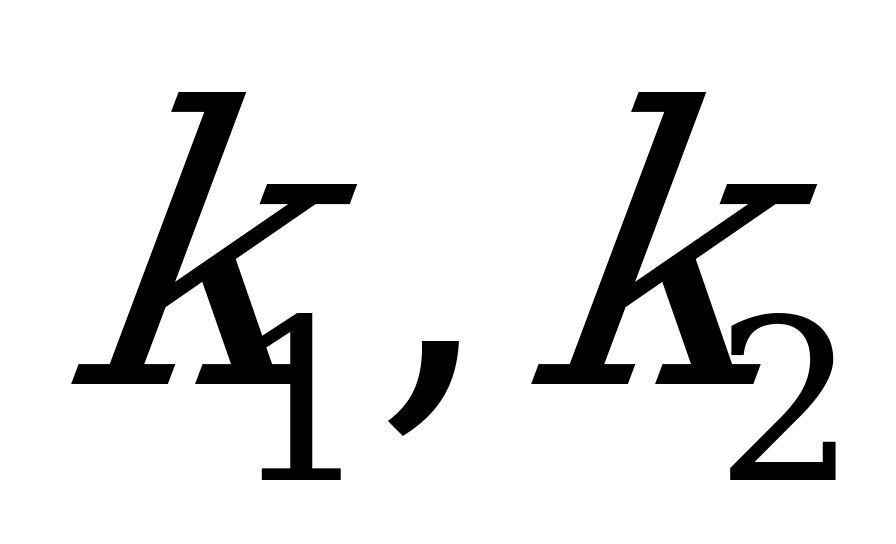. Тогда общее решение ДУ имеет вид: 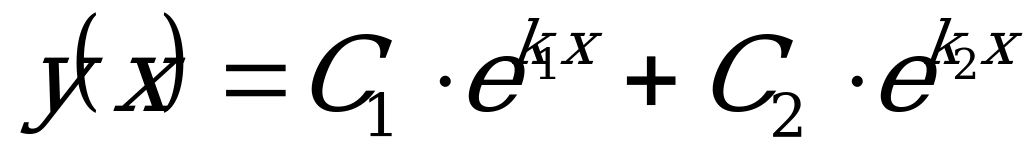, где 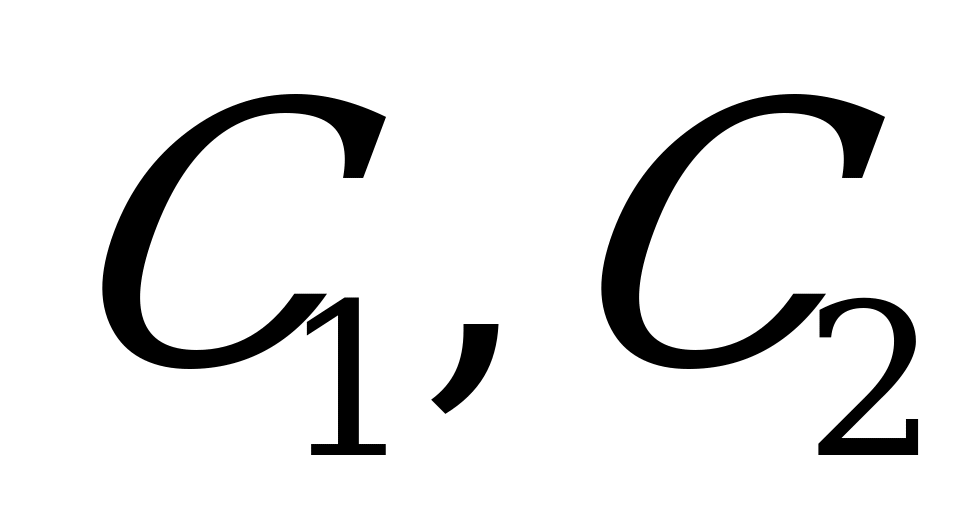- произвольные постоянные.

б) Если 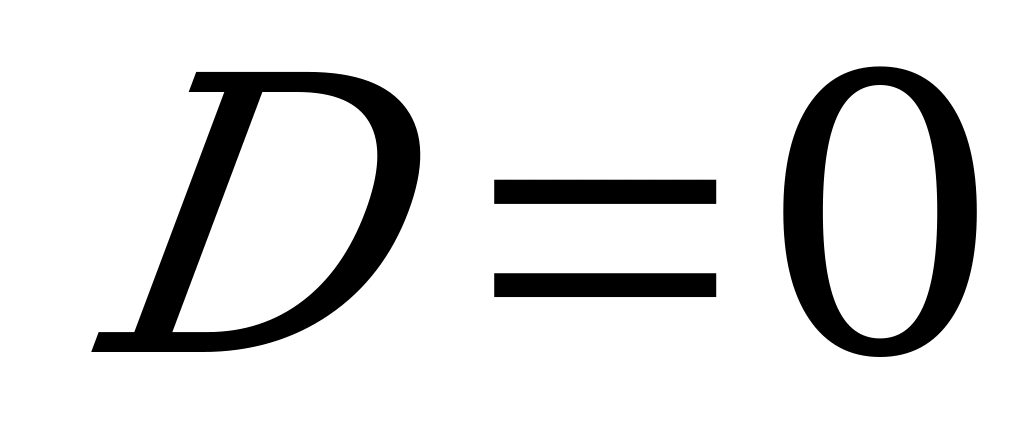, то характеристическое уравнение имеет один действительный корень: 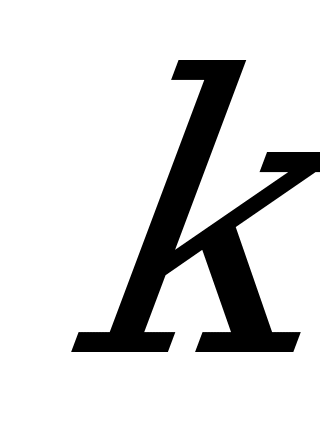. Тогда общее решение ДУ имеет вид: .

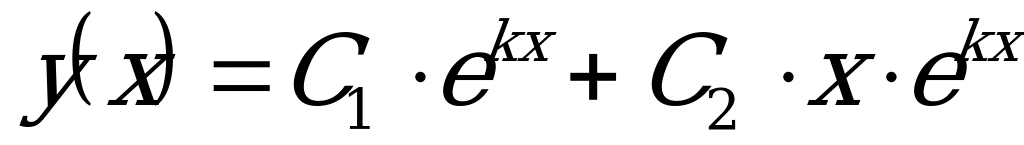в) Если 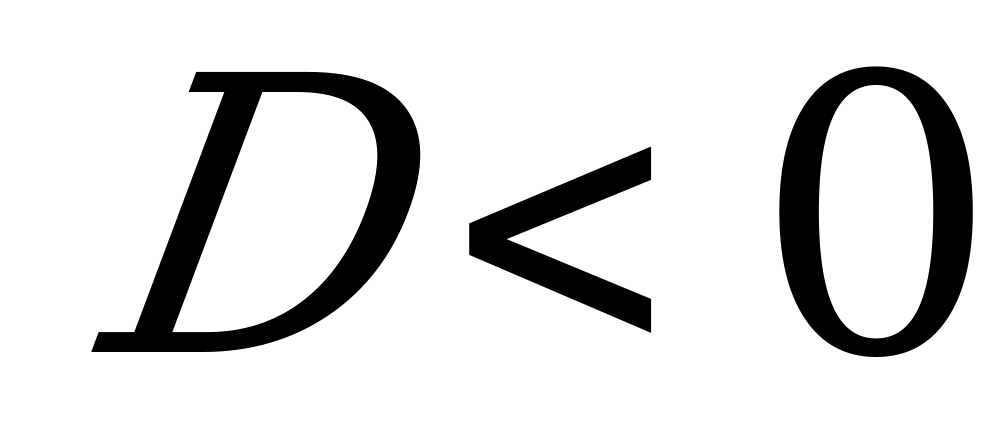, то характеристическое уравнение не имеет действительных корней. Общее решение ДУ в этом случае имеет вид: 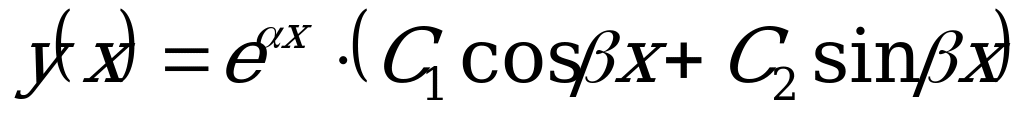, где .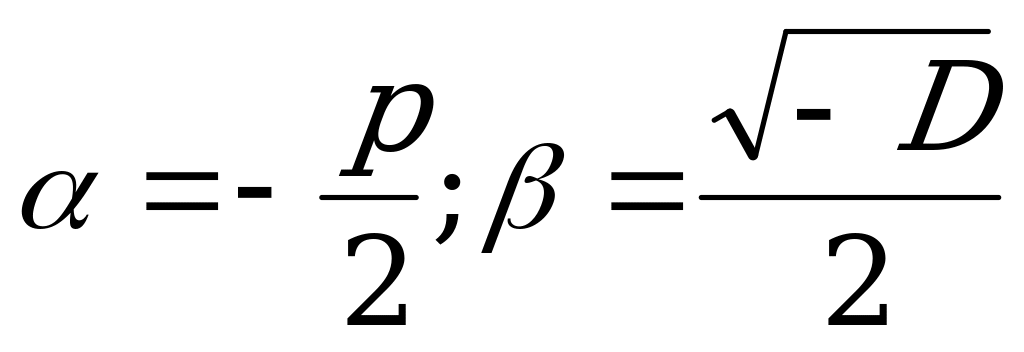

3) Находим частное решение уравнения, используя начальные условия.

Пример 6. Решить уравнение: .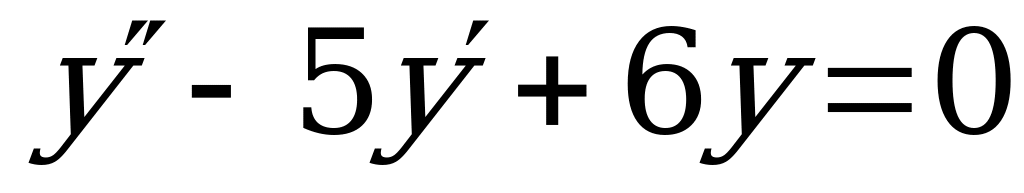

Решение:

1) Составляем характеристическое уравнение, используя замену: :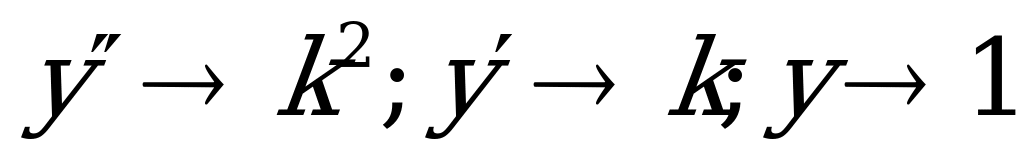

.

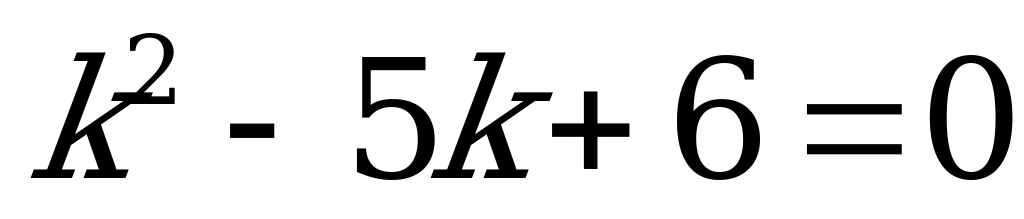2) Решаем полученное квадратное уравнение.

, .

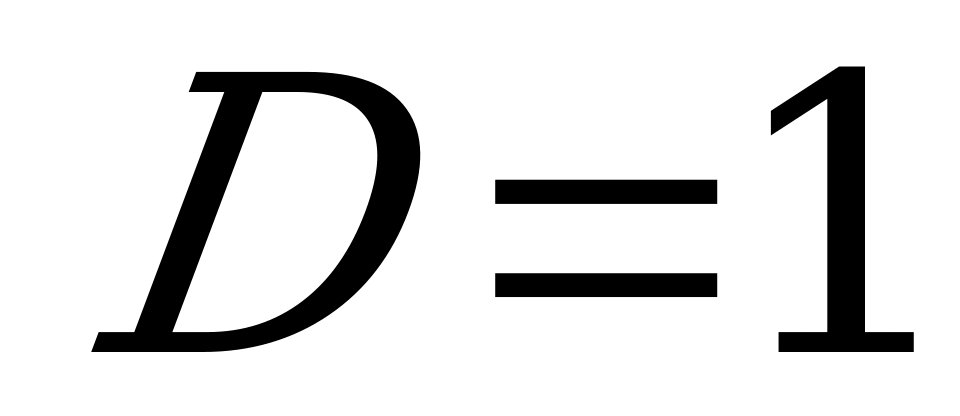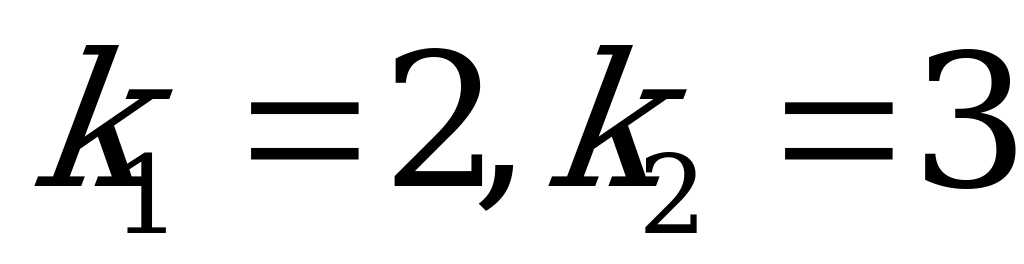Значит, общее решение ДУ имеет вид: .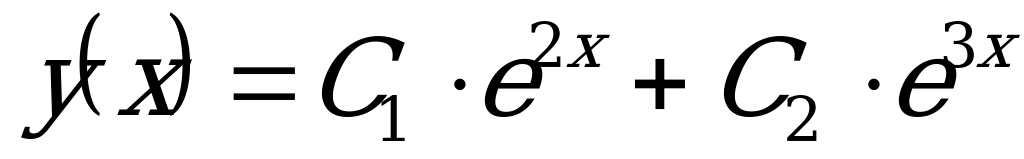

Ответ: .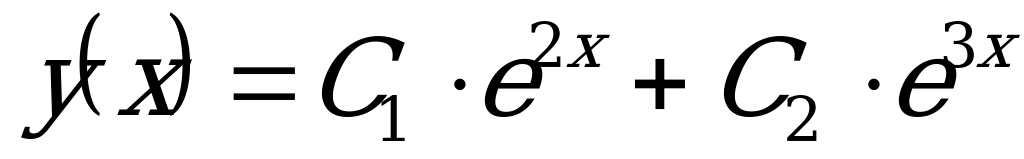

Пример 7. Найти общее решение уравнения: .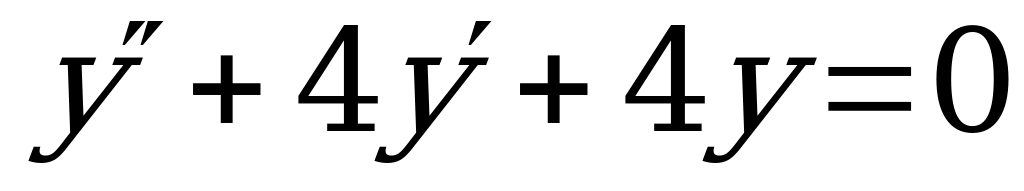

Решение:

1) Составляем характеристическое уравнение: .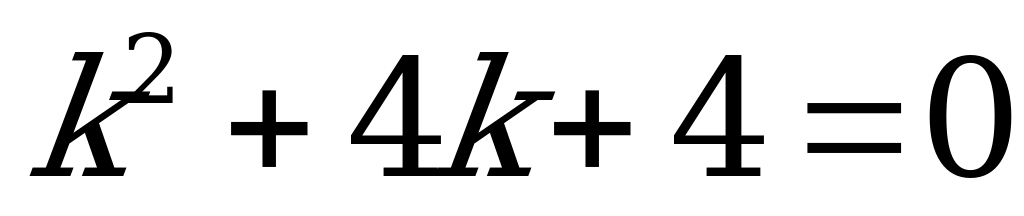

2) Решаем полученное квадратное уравнение.

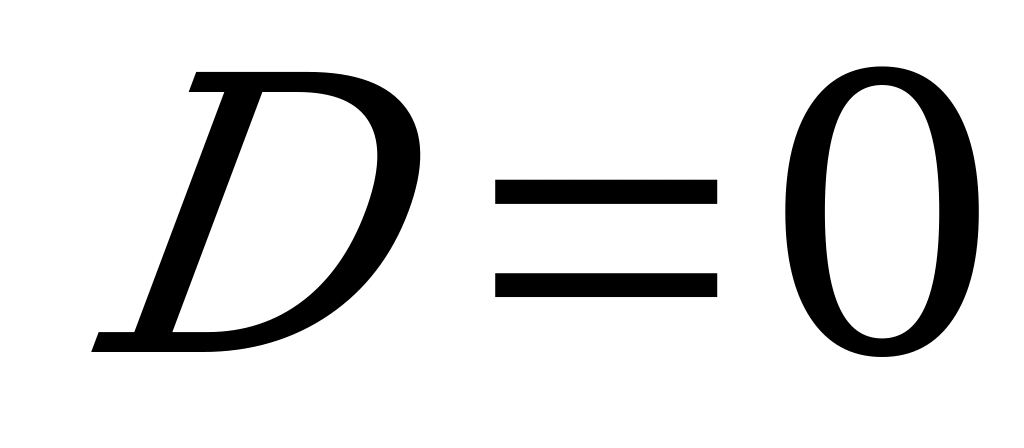, получаем один действительный корень .

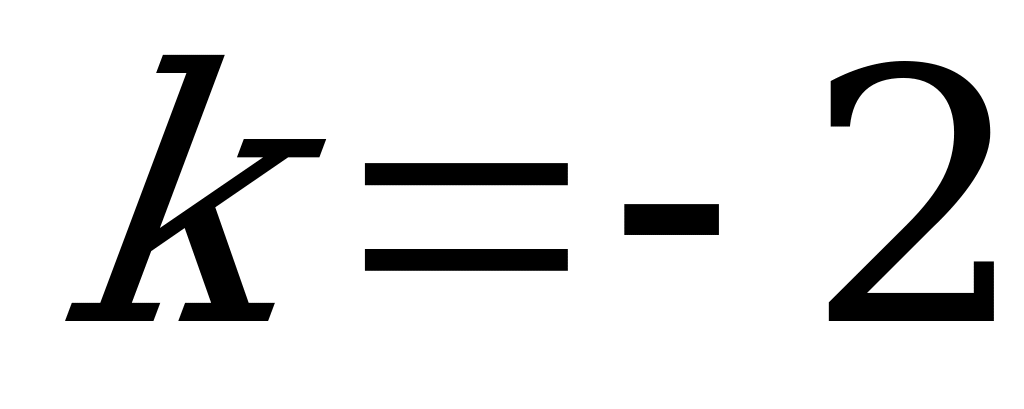Значит, общее решение ДУ имеет вид: .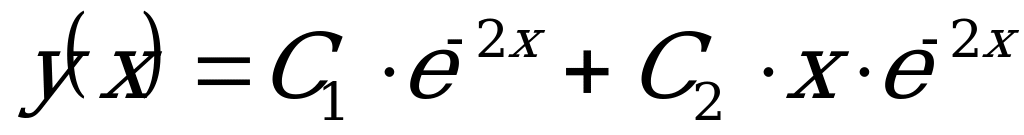

Ответ: .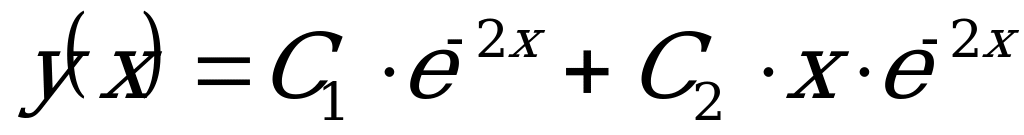

Пример 8. Решить уравнение: .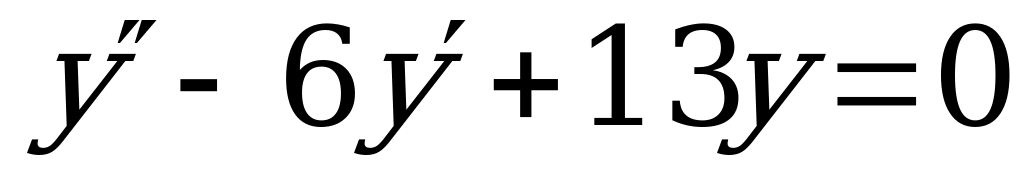

Решение:

1) Составляем характеристическое уравнение: .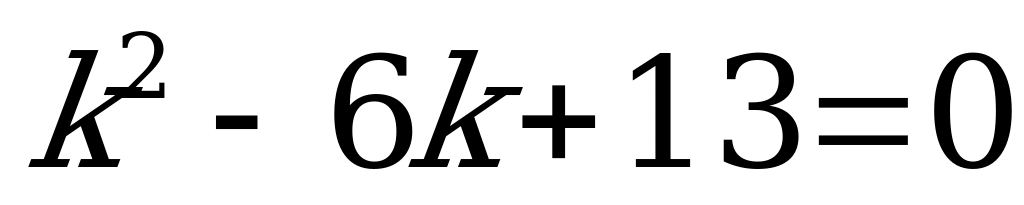

2) Решаем полученное квадратное уравнение.

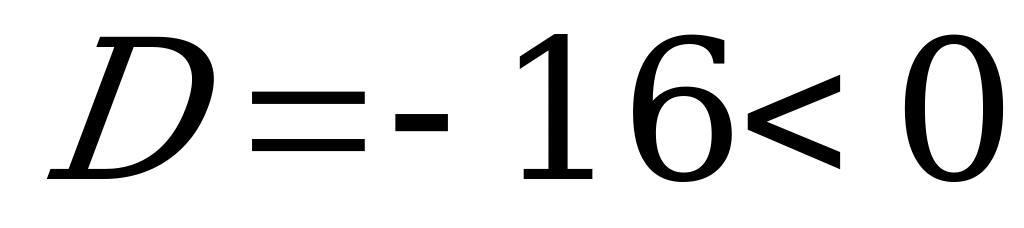, уравнение не имеет действительных корней.

Вычислим значения промежуточных постоянных и : .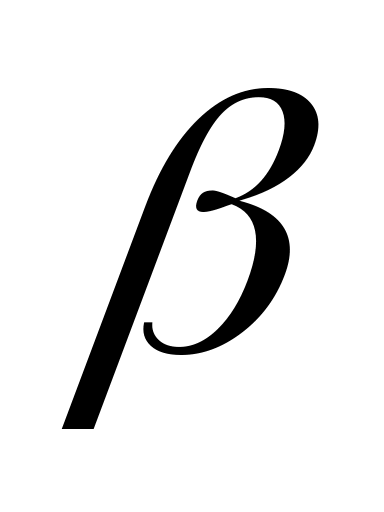

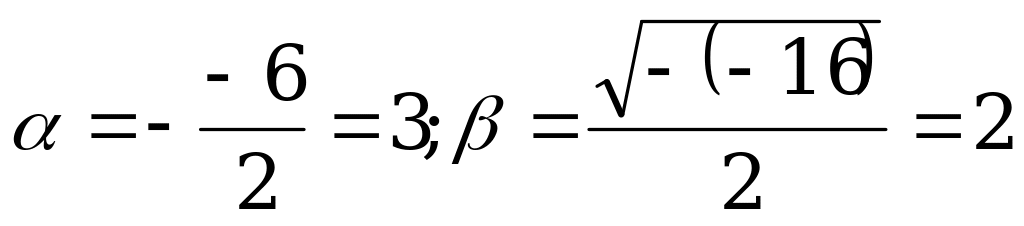Значит, общее решение ДУ имеет вид: .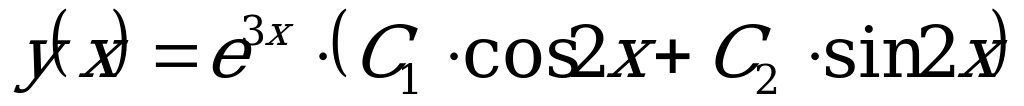

Ответ: 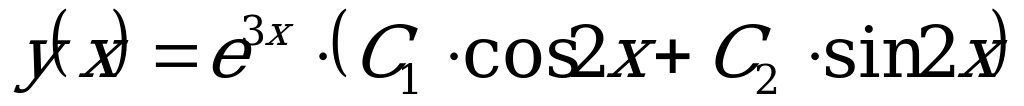.