Презентация урока по теме "Порстые и составные числа" (1 урок)

Простые и составные числа

Изучение нового материала .

1) Простые и составные числа

2) Решето Эратосфена

3) Простые числа – близнецы

4) Магические квадраты , составленные

из простых чисел

5) Совершенные числа

« Числа древние , но вечно юные»

« Ни одному другому разделу

теории чисел не свойственно

столько загадочности и изящества ,

как разделу , занимающемуся

изучением простых чисел».

Мартин Гарднер

Простые и составные числа

Простые и составные числа

Можно сказать, что число

является составным , если его

можно разложить на два множителя ,

ни один из которых не равен 1.

Например: 21 = 3 * 7 .

Простое число , напротив, обладает

« противоположным» свойством :

если оно разложено на два множителя,

то один из них равен 1.

Простые и составные числа

Интерес математиков к простым числам

был огромен , начиная с древнейших

времен. Само понятие простого числа

было введено древнегреческим ученым

Пифагором .

Пифагор

А Евклид доказал , что простых чисел

бесконечно много.

Евклид

Как выбрать простые числа из

некоторого состава натуральных

чисел?

Другими словами, как найти

все простые числа не превосходящие некоторого

натурального числа ?

Ответ на этот вопрос дал греческий математик –

Эратосфен.

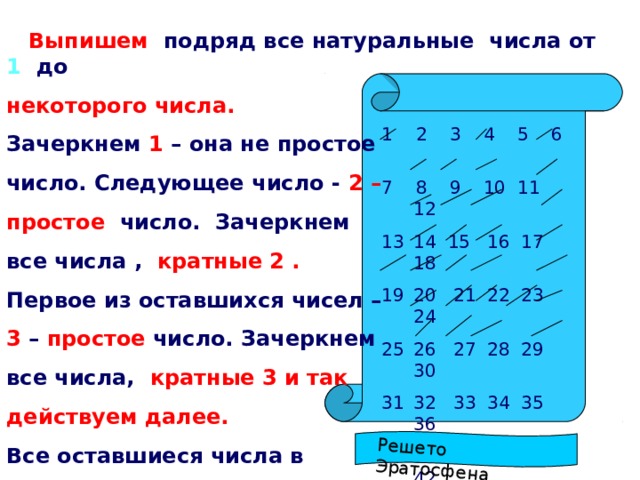
Решето Эратосфена

Выпишем подряд все натуральные числа от 1 до

некоторого числа.

Зачеркнем 1 – она не простое

число. Следующее число - 2 –

простое число. Зачеркнем

все числа , кратные 2 .

Первое из оставшихся чисел –

3 – простое число. Зачеркнем

все числа, кратные 3 и так

действуем далее.

Все оставшиеся числа в

записи – простые .

1 2 3 4 5 6

7 8 9 10 11 12

• 14 15 16 17 18

• 20 21 22 23 24

• 26 27 28 29 30

• 32 33 34 35 36

• 38 39 40 41 42

Решето Эратосфена

В древности писали на восковых

табличках острой палочкой – стилем . Поэтому Эратосфен,

вместо того чтобы вычёркивать

написанные им на табличке

числа, выкалывал их острым

концом стиля. После выкалывания

всех составных чисел табличка

напоминала решето . С тех пор

придуманный Эратосфеном метод

отыскания простых чисел называют

« решетом Эратосфена».

2

16

3

17

4

30

31

44

5

18

45

19

58

32

6

33

20

7

46

59

47

21

8

34

60

9

22

35

61

48

49

23

62

36

10

24

37

11

50

63

51

25

38

64

12

13

26

65

52

39

27

53

66

40

14

15

54

28

41

67

55

29

42

68

56

69

43

57

70

71

• На форзаце учебника помещена
• На форзаце учебника помещена
• На форзаце учебника помещена

таблица простых чисел

от 2 до 997

• таблица простых чисел от 2 до 997
• таблица простых чисел от 2 до 997

Если не принимать во внимание единственное

исключение – числа и , то наименьшее

« расстояние» между

соседними простыми

числами равно .

Простые числа-близнецы

Итак , пару последовательных простых

чисел , разность между которыми равна 2 , мы

назовем БЛИЗНЕЦАМИ.

В первой сотне имеется всего восемь таких пар :

( 3;5);(5;7); ( 11;13); (17;19); ( 29;31);(41;43) ;

( 59;61) ; ( 71;73).

От 1 до 100 000 таких пар 1225 .

Древние греки открыли, что некоторые

числа обладают замечательным

свойством :

сумма всех делителей данного числа

равна самому числу ( само число не

считается делителем ).

Такие числа были названы СОВЕРШЕННЫМИ.

По аналогии , числа меньшие суммы всех делителей

были названы НЕДОСТАТОЧНЫМИ , а числа

большие суммы делителей - ИЗБЫТОЧНЫМИ .

Никомах Герасский , славный грек , знаменитый философ и математик писал :

« Совершенные числа красивы. Но известно, что красивые вещи редки и немногочисленны , безобразные же встречаются в изобилии».

Первым совершенным числом , о котором узнали математики Древней Греции , стало число 6 : 6 = 1 + 2 + 3 ;

Следующее совершенное число – 28 :

28 = 1 + 2 + 4 + 7 + 14 .

В настоящее время известно более 30 совершенных чисел.

Докажи, что приведенные ниже числа являются

составными :

8, 28 , 111 , 77 777.

8 = 2 * 4 ;

28 = 4 * 7 ;

111 = 3 * 37 ;

77 777= 7 * 11 111.

Всеми возможными способами представь в виде

произведения двух множителей числа :

5 , 8 , 9 , 11 , 17 , 28.

При каких значениях x число 1 1 x является

простым ?

Решение

5 = 5 * 1 = 1 * 5 ;

8 = 1 * 8 = 8 * 1 = 2 * 4 = 4 * 2 ;

9 = 1 * 9 = 9 * 1 = 3 * 3 ;

11 = 1 * 11 = 11 * 1 ;

12 = 1 * 12 = 12 * 1 = 3 * 4 = 4 * 3 =

= 2 * 6 = 6 * 2 ;

17 = 1 * 17 = 17 * 1 ;

28 = 28 * 1 = 1 * 28 = 2 * 14 = 14 * 2 =

= 4 * 7 = 7 * 4 .

При x = 1

Вася Иванов находится в комнате

ЛАБИРИНТА , номер которой –

НАИБОЛЬШЕЕ ОДНОЗНАЧНОЕ

ПРОСТОЕ ЧИСЛО.

Путь к выходу ( комната А ) идет

только через комнаты ,номера

которых – ПРОСТЫЕ ЧИСЛА , при

том двери могут быть либо в стенах,

либо в углах комнат :

1

20

34

38

14

21

5

3

37

9

4

26

47

31

30

33

19

23

27

49

44

12

42

6

7

8

32

41

16

29

25

2

11

39

28

43

15

48

24

10

46

17

40

45

35

22

А

36

18

Покажи стрелками путь Васи.

ДОМАШНЕЕ ЗАДАНИЕ

• П. 3.3 учить;
• № 645